NCERT Solutions for Exercise 13.2 Class 10 Maths Chapter 13 -Surface Area and Volumes

NCERT Solutions for Exercise 13.2 Class 10 Maths Chapter 13 - Surface Area and Volumes

Edited By Ramraj Saini | Updated on Nov 27, 2023 05:35 PM IST | #CBSE Class 10th

Upcoming Event

CBSE Class 10th Exam Date : 01 Jan' 2025 - 14 Feb' 2025

NCERT Solutions For Class 10 Maths Chapter 13 Exercise 13.2

NCERT Solutions for Exercise 13.2 Class 10 Maths Chapter 13 Surface Area and Volumes are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 13.2 is concerned with calculating volumes when two or more objects are combined to form a new shape. Unlike the surface area calculation in the previous section, where some of the areas that were not visible were left out, this would not be the case with volume. The volume of the solid created by merging two basic solids of known figure equals the total volume of the constituent solids.

Don't Miss: JEE Main & NEET 2026 Scholarship Test (Class 10): Narayana | Aakash

This Story also Contains

NCERT Solutions For Class 10 Maths Chapter 13 Exercise 13.2
Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 13 exercise 13.2
Assess NCERT Solutions for Class 10 Maths chapter 13 exercise 13.2
More About NCERT Solutions for Class 10 Maths Exercise 13.2
Benefits of NCERT Solutions for Class 10 Maths Exercise 13.2
Key Features For Class 10 Maths Chapter 13 Exercise 13.2
NCERT Solutions Subject Wise

NCERT Solutions for Exercise 13.2 Class 10 Maths Chapter 13 - Surface Area and Volumes

This exercise has eight questions that require students to visualize the shapes as described in the problem statements, then break up the figure, especially those types of figures whose volume or the formula to find its volume is known to us. So that we can very easily determine their volumes and either add them or subtract them to get the final volume of the final resultant figure. 10th class Maths exercise 13.2 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below

Pearson | PTE

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

Apply

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 13 exercise 13.2

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 13 exercise 13.2

Surface Areas and Volumes Class 10 Maths Chapter 13 Exercise: 13.1

Q1 A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of $\pi$ .

Answer:

The volume of the solid is given by :

The volume of solid = Volume of cone + Volume of a hemisphere

The volume of cone :

$=\ \frac{1}{3} \pi r^2h$

or $=\ \frac{1}{3} \pi \times 1^2\times 1$

or $=\ \frac{\pi}{3}\ cm^3$

And the volume of the hemisphere :

$=\ \frac{2}{3}\pi r^3$

or $=\ \frac{2}{3}\pi \times 1^3$

or $=\ \frac{2\pi}{3}\ cm^3$

Hence the volume of solid is :

$=\ \frac{\pi}{3}\ +\ \frac{2\pi}{3}\ =\ \pi\ cm^3$

Q2 Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminum sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)

Answer:

The volume of air present = Volume of cylinder + 2 (Volume of a cone)

Now, the volume of a cylinder : $=\ \pi r^2h$

or $=\ \pi \left ( \frac{3}{2} \right )^2\times 8$

or $=\ 18\pi \ cm^3$

And the volume of a cone is :

$=\ \frac{1}{3} \pi r^2h$

or $=\ \frac{1}{3} \pi \times \left ( \frac{3}{2} \right )^2\times 2$

or $=\ \frac{3}{2} \pi \ cm^3$

Thus the volume of air is :

$=\ 18 \pi\ +\ 2\times \frac{3}{2} \pi \ =\ 21\pi$

or $=\ 66\ cm^3$

Q3 A gulab jamun contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (see Fig).

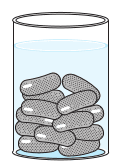
1636092497555

Answer:

It is clear from the figure that gulab jamun has one cylindrical part and two hemispherical parts.

Thus, the volume of gulab jamun is = Volume of cylindrical part + 2 (Volume of the hemisphere )

Now, the volume of the cylinder is $=\ \pi r^2h$

or $=\ \pi\times 1.4^2\times 2.2$

or $=\ 13.55\ cm^3$

And the volume of a hemisphere is :

$\\=\ \frac{2}{3}\pi r^3\\\\=\ \frac{2}{3}\times \pi \times (1.4)^3\\\\=\ 5.75\ cm^3$

Thus the volume of 1 gulab jamun is $= 13.55 + 2 (5.75) = 25.05 cm^3.$

Hence the volume of 45 gulab jamun

Further, it is given that one gulab jamun contains sugar syrup upto .

So, the total volume of sugar present :

$=\ \frac{30}{100}\times 1127.25\ =\ 338\ cm^3$

Q4 A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand (see Fig. 13.16).

SURFACE AREAS AND VOLUMES

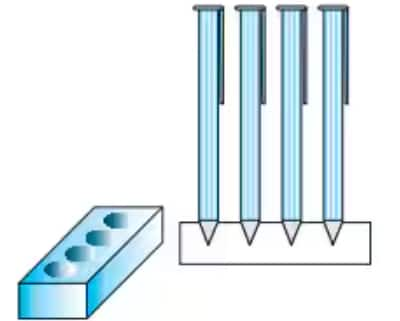
Answer:

The volume of wood is given by = volume of the cuboid - the volume of four cones.

Firstly, the volume of cuboid : $=\ lbh$

or $=\ 15\times 10\times 3.5$

or $=\ 525\ cm^3$

And, the volume of cone :

$\\=\ \frac{1}{3} \pi r^2h\\=\ \frac{1}{3} \pi \times (0.5)^2\times 1.4\\\\=\ 0.3665\ cm^3$

Thus the volume of wood is $= 525 + 4 (0.3665) = 523.53 \:cm^3$

Q5 A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.

Answer:

According to the question :

Water spilled from the container = Volume of lead balls.

Let us assume the number of lead balls to be n.

Thus the equation becomes :

$\frac{1}{4}\times Volume_{cone}\ =\ n\times \frac{4}{3} \pi r^3$

or $\frac{1}{4}\times \frac{1}{3}\pi\times5^2\times 8\ =\ n\times \frac{4}{3} \pi\times 0.5^3$

or $n\ =\ \frac{25\times 8}{16\times \left ( \frac{1}{2} \right )^3}$

or $n\ =\ 100$

Hence the number of lead shots dropped is 100.

Q6 A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm 3 of iron has approximately 8g mass. (Use $\pi = 3.14$ )

Answer:

The pole can be divided into one large cylinder and one small cylinder.

Thus, the volume of pole = volume of large cylinder + volume of a small cylinder

$=\ \pi r_l^2h_l\ +\ \pi r_s^2h_s$

or $=\ \pi \times 12^2\times 220\ +\ \pi \times 8^2\times 60$

or $=\ \pi \times \left ( 144\times 220\ +\ 64\times 60 \right )$

or $=\ 3.14\times 35520$

or $=\ 111532.5\ cm^3$

Now, according to question mass of the pole is :

$=\ 8\times 111532.5$

or $=\ 892262.4\ g\ =\ 892.262\ Kg$

Q7 A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.

Answer:

It is clear from the question that the required volume is :

The volume of water (left) =Volume of a cylinder - Volume of solid

Now the volume of the cylinder is $=\ \pi r^2h$

or $=\ \pi\times (60)^2\times 180\ cm^3$

And the volume of solid is :

$\\=\ \frac{1}{3} \pi r^2h\ +\ \frac{2}{3}\pi r^3\\\\=\ \frac{1}{3} \times \pi \times (60)^2\times 120\ +\ \frac{2}{3}\times \pi \times (60)^3\\\\=\ \pi (60)^2\times 80\ cm^3$

Thus the volume of water left :

$\\=\ \pi (60)^2\times 180\ -\ \pi (60)^2\times 80\\\\=\ \pi (60)^2\times 100\\\\=\ 1131428.57\ cm^3\\\\=\ 1.131\ m^3$

Q8 A spherical glass vessel has a cylindrical neck 8 cm long, 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm 3 . Check whether she is correct, taking the above as the inside measurements, and $\pi = 3.14$ .

Answer:

The volume of the vessel is given by :

The volume of vessel = Volume of sphere + Volume of the cylindrical part

Now, the volume of the sphere is :

$\\=\ \frac{4}{3}\pi r^3\\\\=\ \frac{4}{3}\pi \left ( \frac{8.5}{2} \right )^3\\\\=\ 321.55\ cm^3$

And the volume of the cylinder is:-

$\\=\ \pi r^2h\\\\=\ \pi \times (1)^2\times 8\\\\=\ 25.13\ cm^3$

Thus the volume of the vessel is $= 321.55 + 25.13 = 346.68\: cm^3$

Benefits of NCERT Solutions for Class 10 Maths Exercise 13.2

Exercise 13.2 Class 10 Maths, is based on Volume of a Combination of Solids.
Class 10 Maths chapter 13 exercise 13.2 helps us in understanding complex shapes and finding its volume.
Class 10 Maths chapter 13 exercise 13.2 helps us to simplify complex shapes by breaking it into smaller individual objects that are simple to our understanding.

Key Features For Class 10 Maths Chapter 13 Exercise 13.2

Step-by-Step Solutions: Clear and detailed explanations for each problem in Ex 13.2 class 10, ensuring students understand the methodology.
Conceptual Understanding: Explanation of surface area and volume concepts involved in the exercises, aiding students in grasping the underlying principles are discussed in class 10 maths ex 13.2.
Variety of Problems: In class 10 ex 13.2, diverse types of problems, offering a broad spectrum of challenges to reinforce understanding.
Visual Aids, Diagrams, and Examples: Use of visual representations, diagrams, and real-life examples to simplify complex concepts and aid visual learners.
Application-Based Problems: In 10th class maths exercise 13.2 answers, application-oriented problems that relate statistics to real-world scenarios, fostering practical understanding and problem-solving skills.

Also See:

NCERT Solutions for Class 10 Maths Chapter 13- Surface Area and Volume