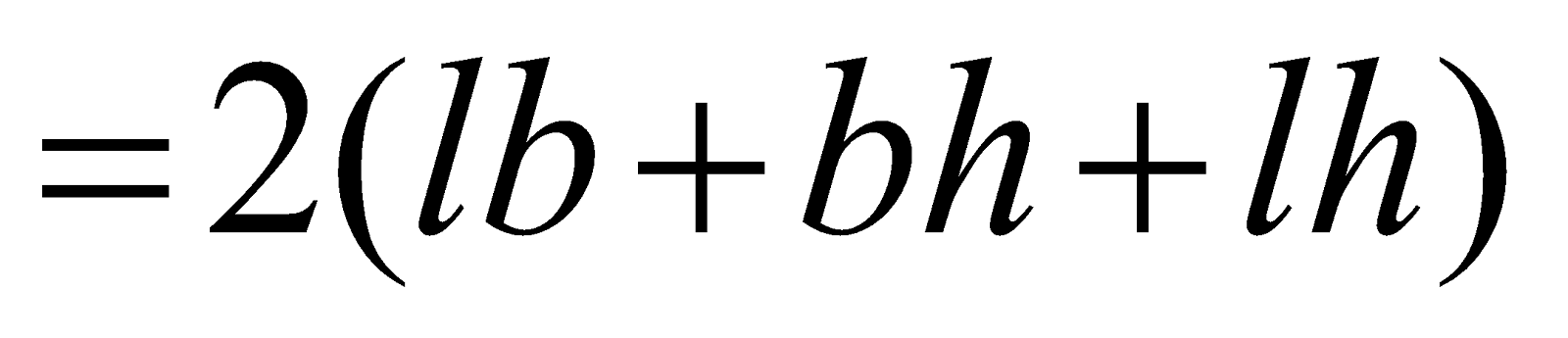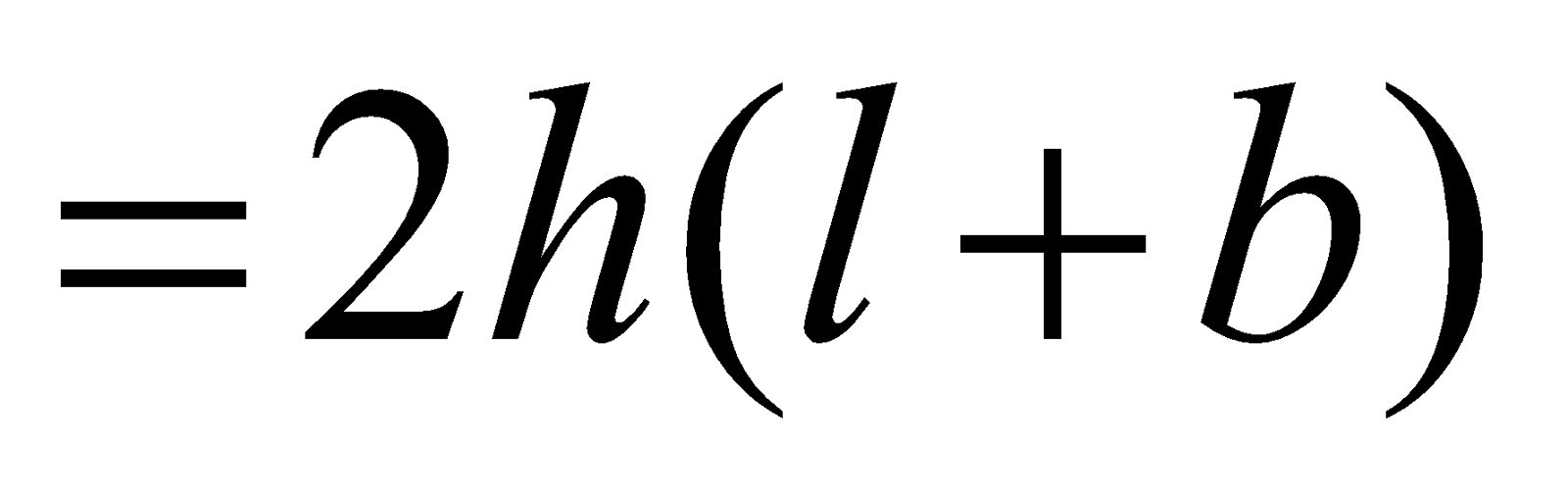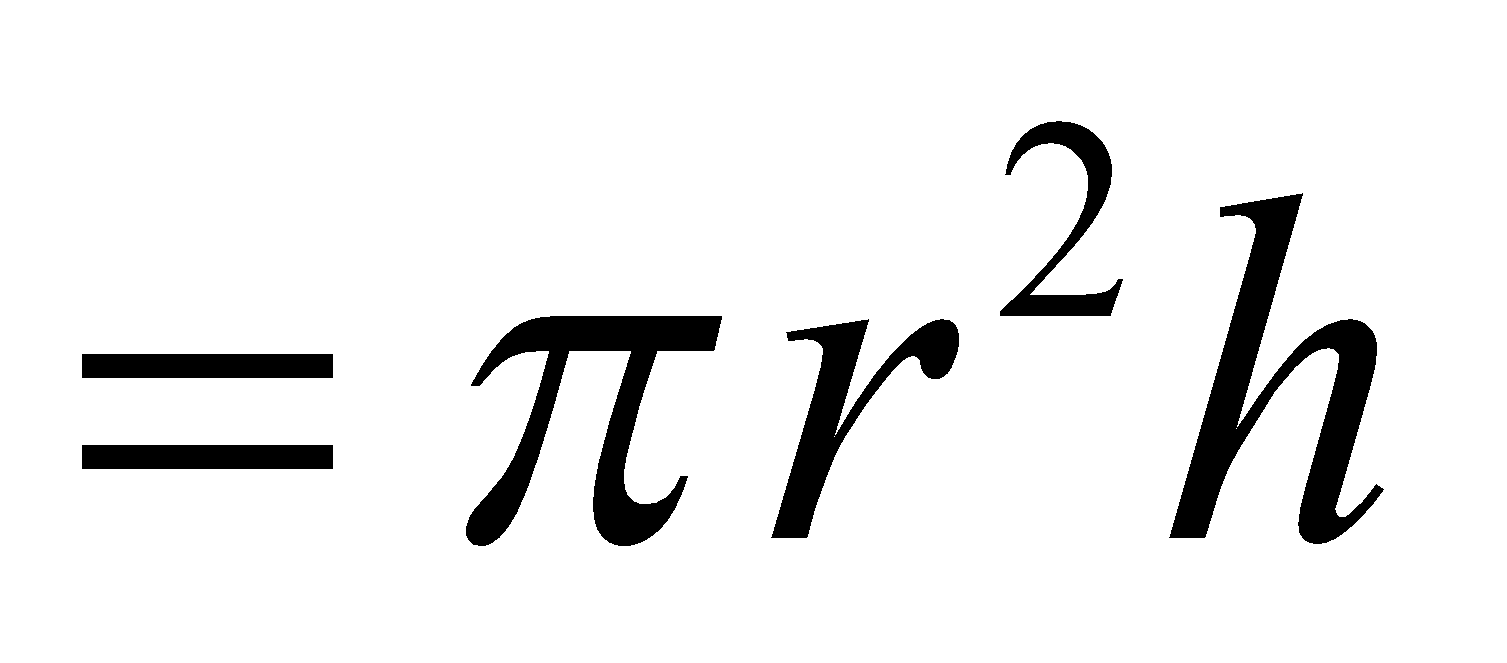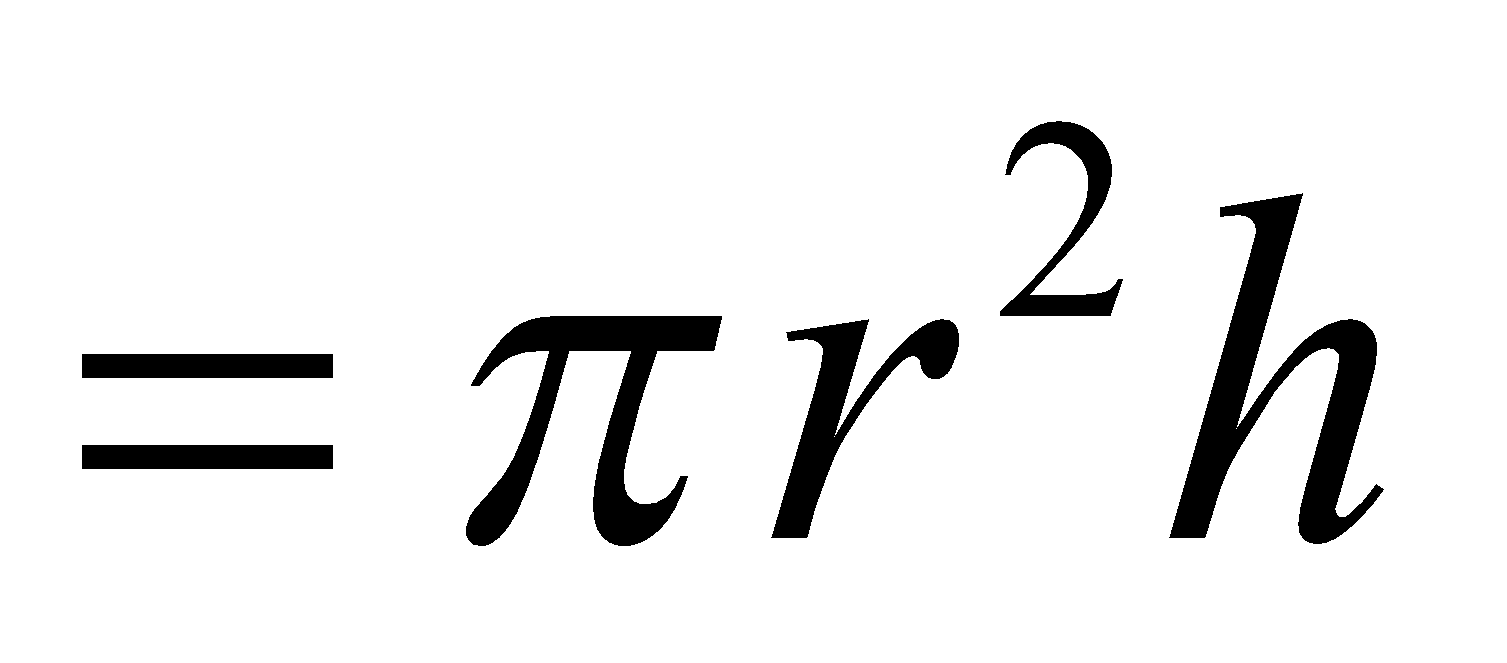Surface Areas and Volumes Class 10 Chapter 13 Excercise: 13.5
Answer:
A number of rounds are calculated by :
$=\ \frac{Height\ of\ cylinder }{Diameter\ of\ wire}$
$=\ \frac{12 }{0.3}\ =\ 40\ rounds$
Thus the length of wire in 40 rounds will be $=\ 40\times 2\pi \times 5\ =\ 400 \pi\ cm\ =\ 12.57\ m$
And the volume of wire is: Area of cross-section $\times$ Length of wire
$=\pi \times (0.15)^2\times 1257.14$
$=\ 88.89\ cm^3$
Hence the mass of wire is. $=\ 88.89\ \times 8.88\ =\ 789.41\ gm$
Answer:
The volume of the double cone will be = Volume of cone 1 + Volume of cone 2.
$=\ \frac{1}{3}\ \pi r^2h_1\ +\ \frac{1}{3}\ \pi r^2h_2$
$=\ \frac{1}{3}\ \pi \times 2.4^2\times 5$ (Note that sum of heights of both the cone is 5 cm - hypotenuse).
$=\ 30.14\ cm^3$
Now the surface area of a double cone is :
$=\ \pi rl_1\ +\ \pi rl_2$
$=\ \pi \times 2.4 \left ( 4\ +\ 3 \right )$
$=\ 52.8\ cm^2$
Answer:
The total volume of the cistern is : $=\ 150\times 120\times 110\ =\ 1980000\ cm^3$
And the volume to be filled in it is $= 1980000 - 129600\ =\ 1850400\ cm^3$
Now let the number of bricks be n.
Then the volume of bricks : $= n\times 22.5\times 7.5\times 6.5 \ =\ 1096.87n\ cm^3$
Further, it is given that brick absorbs one-seventeenth of its own volume of water.
Thus water absorbed :
$=\ \frac{1}{17}\times 1096.87n\ cm^3$
Hence we write :
$1850400\ +\ \frac{1}{17}( 1096.87n)\ =\ 1096.87n$
$n\ =\ 1792.41$
Thus the total number of bricks is 1792.
Answer:
Firstly we will calculate the volume of rainfall :
Volume of rainfall :
$=\ 7280\times \frac{10}{100\times 1000}$
$=\ 0.7280\ Km ^3$
And the volume of the three rivers is :
$=\ 3\left ( 1072\times \frac{75}{1000}\times \frac{3}{1000} \right )\ Km^3$
$=\ 0.7236\ Km ^3$
It can be seen that both volumes are approximately equal to each other.
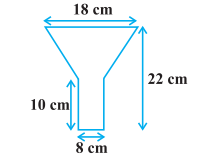
Answer:
From this, we can write the values of both the radius (upper and lower) and the height of the frustum.
Thus slant height of frustum is :
$=\ \sqrt{\left ( r_1\ -\ r_2 \right )^2\ +\ h^2}$
$=\ \sqrt{\left ( 9\ -\ 4 \right )^2\ +\ 12^2}$
$=\ 13\ cm$
Now, the area of the tin shed required :
= Area of frustum + Area of the cylinder
$=\ \pi \left ( r_1\ +\ r_2 \right )l\ +\ 2\pi r_2h$
$=\ \pi \left ( 9\ +\ 4 \right )13\ +\ 2\pi \times 4\times 10$
$=\ 782.57\ cm^2$
Answer:
In the case of the frustum, we can consider:- removing a smaller cone (upper part) from a larger cone.
So the CSA of frustum becomes:- CSA of bigger cone - CSA of the smaller cone
$\\=\ \pi r_1l_1\ -\ \pi r_2 (l_1\ -\ l)\\\\=\ \pi r_1\left ( \frac{lr_1}{r_1\ -\ r_2} \right )\ -\ \pi r_2\left ( \frac{r_1l}{r_1\ -\ r_2}\ -\ l \right )\\\\=\ \left ( \frac{\pi r_1^2 l}{r_1\ -\ r_2} \right )\ -\ \left ( \frac{\pi r_2^2 l}{r_1\ -\ r_2} \right )\\\\=\ \pi l\left ( \frac{r_1^2\ -\ r_2^2}{r_1\ -\ r_2} \right )\\\\=\ \pi l\left ( r_1\ +\ r_2 \right )$
And the total surface area of the frustum is = CSA of frustum + Area of upper circle and area of lower circle.
$=\ \pi l\left ( r_1\ +\ r_2 \right )\ +\ \pi r_1^2\ +\ \pi r_2^2$
Answer:
Similar to how we find the surface area of the frustum.
The volume of the frustum is given by-
=Volume of the bigger cone - Volume of the smaller cone
$=\ \frac{1}{3} \pi r^2_1 h_1\ -\ \frac{1}{3} \pi r^2_2 (h_1\ -\ h)$
$=\ \frac{\pi}{3}\left ( r_1^2 h_1\ -\ r_2^2 (h_1\ -\ h) \right )$
$=\ \frac{\pi}{3}\left ( r_1^2 \left ( \frac{hr_1}{r_1\ -\ r_2} \right )\ -\ r_2^2 \left ( \frac{hr_1}{r_1\ -\ r_2}\ -\ h \right ) \right )$
$=\ \frac{\pi}{3}\left ( \frac{hr_1^3}{r_1\ -\ r_2}\ -\ \frac{hr_2^3}{r_1\ -\ r_2} \right )$
$=\ \frac{\pi}{3}h\left ( \frac{r_1^3\ -\ r_2^3}{r_1\ -\ r_2} \right )$
$=\ \frac{1}{3} \pi h\left ( r_1^2\ +\ r_2^2\ +\ r_1r_2 \right )$