NCERT Solutions for Exercise 13.3 Class 10 Maths Chapter 13 - Surface Area and Volumes
NCERT Solutions For Class 10 Maths Chapter 13 Exercise 13.3
NCERT Solutions for Exercise 13.3 Class 10 Maths Chapter 13 Surface Area and Volumes are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 Maths ex 13.3 concentrate on solids conversion. For example, a cylinder-shaped candle can be melted and poured into a cubical container. The candle has been reshaped into a different shape. The volume of the candle remains constant, which is interesting to note. Students can determine that an object's volume remains constant even when it is converted from one solid shape to another.
With the help of this exercise students understand that when Solids are remoulded and melted to change their shape, but their volume remains the same. With this understanding, students will be able to create equations. If students are asked to find the height of a shape in a question, they can simply equate the two equations where the volume is the same. They will be able to locate the missing dimension in this manner. 10th class Maths exercise 13.3 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.
Assess NCERT Solutions for Class 10 Maths chapter 13 exercise 13.3
Surface Areas and Volumes Class 10 Maths Chapter 13 Exercise: 13.3
Answer:
Let us assume the height of the cylinder to be h.
Since the material is melted and recast thus its volume will remain the same.
So, Volume of sphere = Volume of obtained cylinder.
$\frac{4}{3}\pi r^3_s\ =\ \pi r^2_c h$
$\frac{4}{3}\pi \times 4.2^3\ =\ \pi \times 6^2 \times h$
$h\ =\ \frac{4}{3}\times \frac{4.2\times4.2\times 4.2}{36}$
$h\ =\ 2.74\ cm$
Hence the height of the cylinder is 2.74 cm.
Answer:
According to the question, small spheres are melted and converted into a bigger sphere. Thus the sum of their volume is equal to the volume of the bigger sphere.
The volume of 3 small spheres = Volume of bigger sphere
Let us assume the radius of the bigger sphere is r.
$\frac{4}{3}\pi \left ( r^3_1\ +\ r^3_2\ +\ r^3_3 \right )\ =\ \frac{4}{3}\pi r^3$
$r^3_1\ +\ r^3_2\ +\ r^3_3 \ =\ r^3$
$r^3\ =\ 6^3\ +\ 8^3\ +\ 10^3$
$r\ =\ 12\ cm$
Hence the radius of the sphere obtained is 12 cm.
Answer:
According to the question, the volume of soil dug will be equal to the volume of the platform created.
Thus we can write :
The volume of soil dug = Volume of platform
$\\\Rightarrow \pi r^2h\ =\ Area\times h\\\\\Rightarrow \pi \times \left ( \frac{7}{2} \right )^2\times 20\ =\ 22\times 14 \times h\\\\\Rightarrow h\ =\ \frac{5}{2}\ m$
Thus the height of the platform created is 2.5 m.
Answer:
According to the question, the volume is conserved here :
The volume of soil dug out = Volume of the embankment made.
Let the height of the embankment is h.
$\\\pi r^2_1h'\ =\ \pi\left ( r^2_2\ -\ r^2_1 \right )h\\\\\pi \left ( \frac{3}{2} \right )^2\times 14\ =\ \pi\left ( \left ( \frac{11}{2} \right )^2\ -\ \left ( \frac{3}{2} \right )^2 \right )h\\\\h\ =\ \frac{9}{8}\ m$
Hence the height of the embankment made is 1.125 m.
Answer:
Let the number of cones that can be filled with ice cream be n.
Then we can write :
The volume of a cylinder containing ice cream = n ( volume of 1 ice cream cone )
$\\\pi r^2_{cy}h_{cy}\ =\ n\left ( \frac{1}{3}\pi r^2_{co}h_{co}\ +\ \frac{2}{3} \pi r^3 \right )\\\\\pi\times 6^2\times 15\ =\ n\left ( \frac{1}{3}\times \pi \times 3^2 \times 12\ +\ \frac{2}{3} \pi \times 3^3 \right )\\\\n\ =\ \frac{36\times 15}{54}\\\\n=\ 10$
Hence the number of cones that can be filled is 10.
Answer:
Let us assume the number of coins that need to be melted be n.
Then we can write :
The volume of n coins = Volume of cuboid formed.
$n\left ( \pi r^2 h \right )\ =\ lbh'$
$n\left ( \pi \times \left ( \frac{1.75}{2} \right )^2\times 0.2 \right )\ =\ 5.5\times 10\times 3.5$
$n\ =\ 400$
Thus the required number of coins is 400.
Answer:
According to question volume will remain constant thus we can write :
The volume of bucket = Volume of heap formed.
$\pi r^2_1h_1\ =\ \frac{1}{3}\pi r^2_2 h_2$
Let the radius of heap be r.
$\pi\times 18^2 \times 32\ =\ \frac{1}{3}\times \pi \times r^2\times 24$
$r\ =\ 18\times 2\ =\ 36\ cm$
And thus the slant height will be
$l\ =\ \sqrt{r^2\ +\ h^2}$
$=\ \sqrt{36^2\ +\ 24^2}$
$=\ 12\sqrt{13}\ cm$
Hence the radius of heap made is 36 cm and its slant height is $12\sqrt{13}\ cm$ .
Answer:
Speed of water is: 10 Km/hr
And the volume of water flow in 1 minute is :
$=\ 9\times \frac{10000}{60}\ =\ 1500\ m^3$
Thus the volume of water flow in 30 minutes will be : $=\ 1500\ \times 30\ =\ 45000\ m^3$
Let us assume irrigated area be A. Now we can equation the expression of volumes as the volume will remain the same.
$45000\ =\ \frac{A\times 8}{100}$
$A\ =\ 562500\ m^2$
Thus the irrigated area is $562500 \:m^2$ .
Answer:
Area of the cross-section of pipe is $=\ \pi r^2$
$=\ \pi (0.1)^2\ =\ 0.01 \pi\ m^2$
Speed of water is given to be = 3 km/hr
Thus, the volume of water flowing through a pipe in 1 min. is
$=\ \frac{3000}{60}\times 0.01 \pi$
$=\ 0.5 \pi\ m^3$
Now let us assume that the tank will be completely filled after t minutes.
Then we write :
$t\times 0.5 \pi\ =\ \pi r^2h$
$t\times 0.5 \ =\ 5^2\times 2$
$t\ =\ 100$
Hence the time required for filling the tank completely in 100 minutes.
Answer:
Area of the cross-section of pipe is $=\ \pi r^2$
$=\ \pi (0.1)^2\ =\ 0.01 \pi\ m^2$
Speed of water is given to be = 3 km/hr
Thus, the volume of water flowing through a pipe in 1 min. is
$=\ \frac{3000}{60}\times 0.01 \pi$
$=\ 0.5 \pi\ m^3$
Now let us assume that the tank will be completely filled after t minutes.
Then we write :
$t\times 0.5 \pi\ =\ \pi r^2h$
$t\times 0.5 \ =\ 5^2\times 2$
$t\ =\ 100$
Hence the time required for filling the tank completely in 100 minutes.
More About NCERT Solutions for Class 10 Maths Exercise 13.3 –
There are many different shapes and sizes in geometry, such as the sphere, cube, cuboid, cone, cylinder, and so on. Each shape has a volume and a surface area. However, we can only measure the area covered by two-dimensional figures such as squares, circles, rectangles, triangles, and so on, and there is no volume available.
The total surface area includes the base(s) as well as the curved part. The area of only the curved part of a shape, excluding its base, is referred to as curved surface area (s). For shapes like a cylinder, it's also known as lateral surface area.
NCERT syllabus class 10 maths chapter 13 Some important formulas are:
Volume of cone 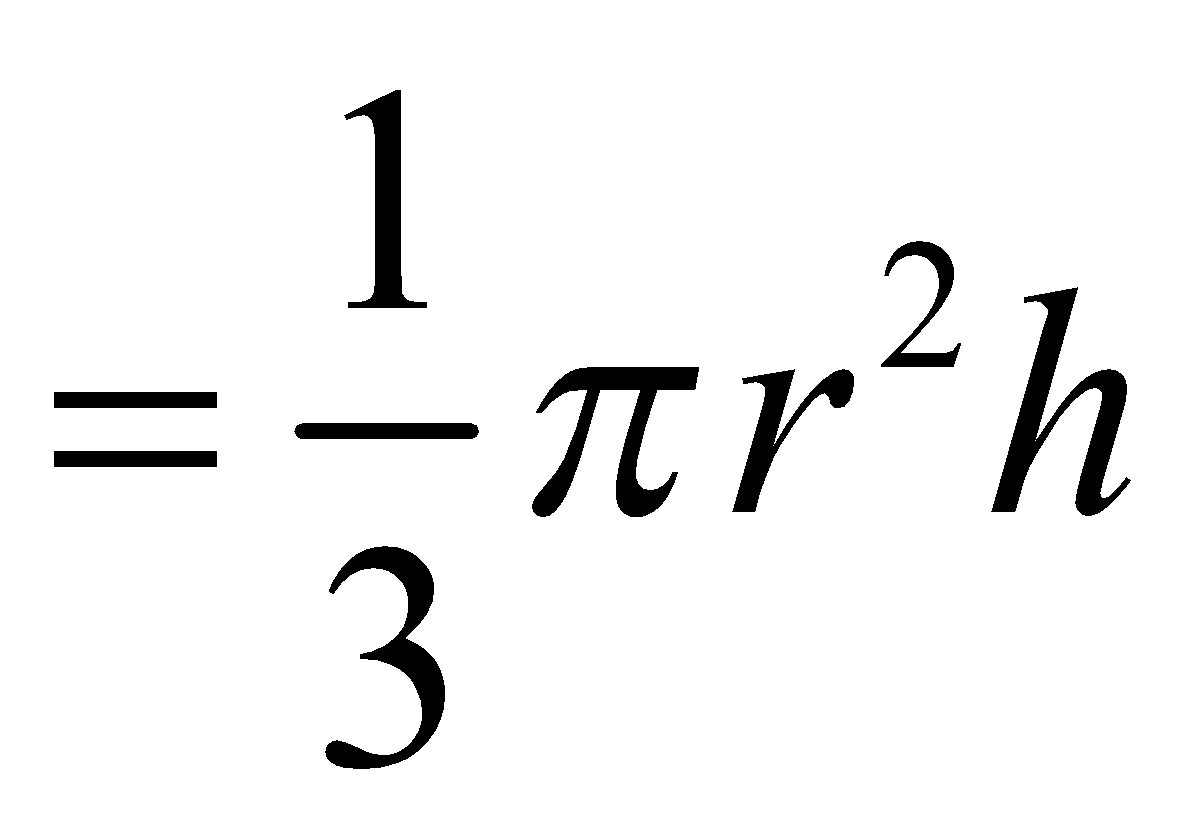
Volume of cylinder 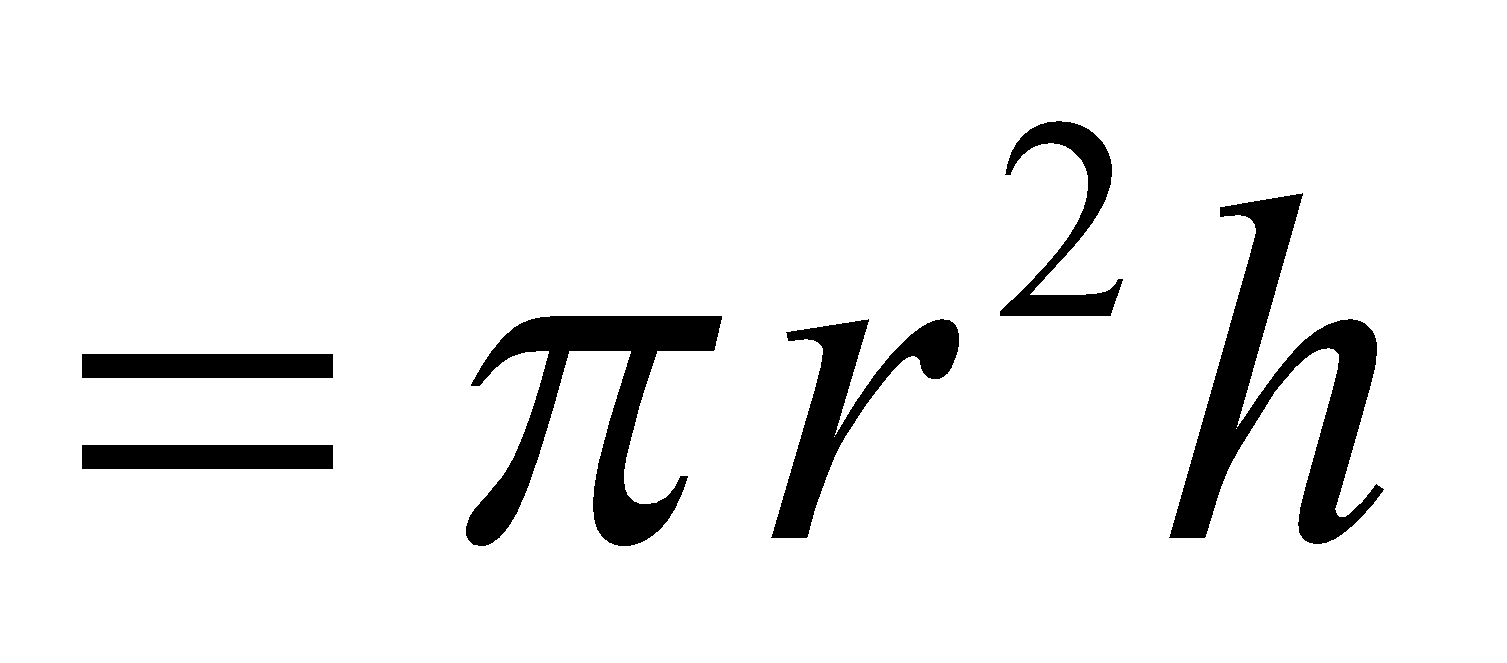
Volume of sphere 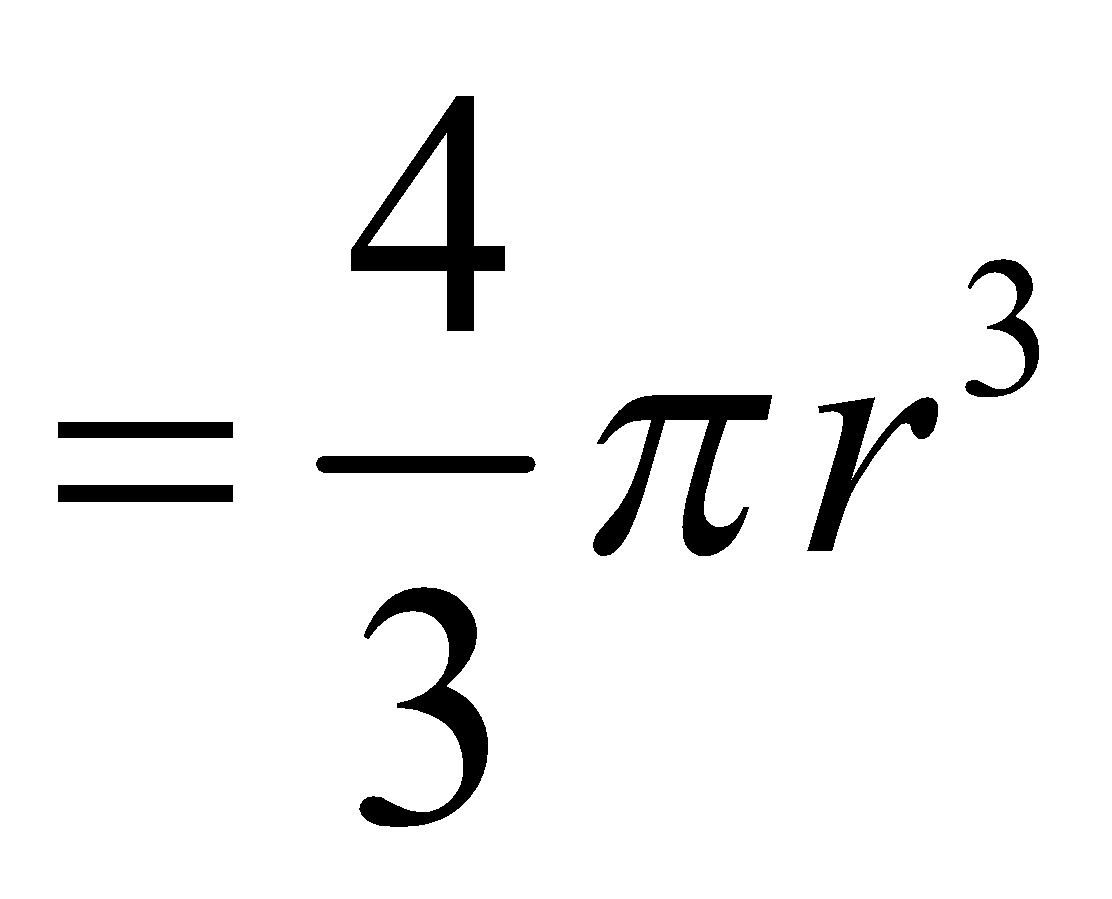
Volume of cuboid 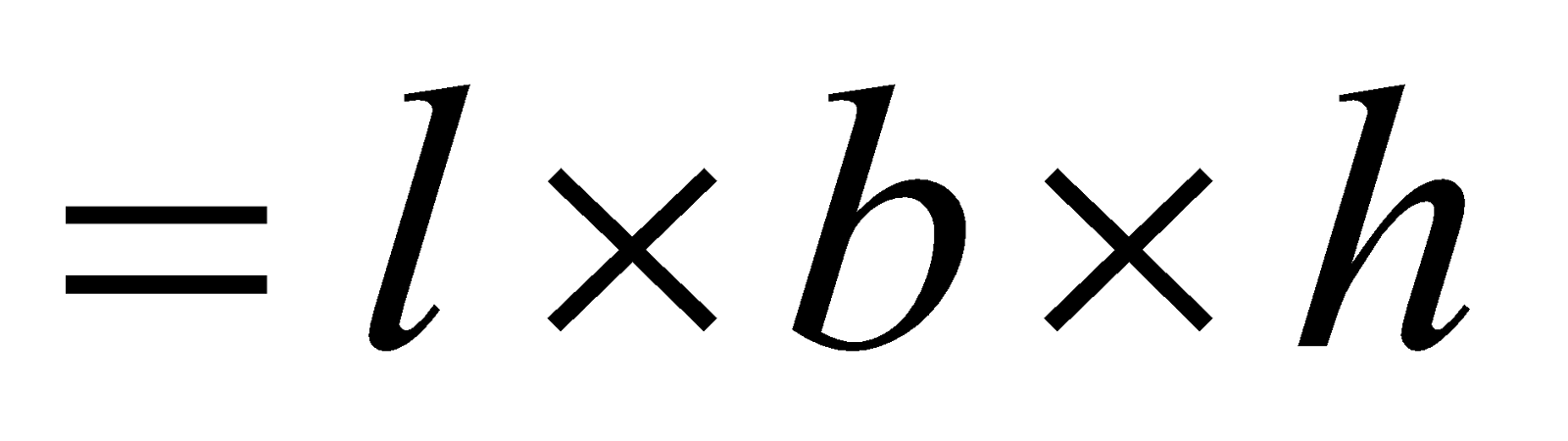
Also Read| Surface Areas and Volumes Class 10 Notes
Benefits of NCERT Solutions for Exercise 13.3 Class 10 Maths Chapter 13
- Exercise 13.3 Class 10 Maths is based on Conversion of Solid from One Shape to Another teaching us about shape conversion due to melting and recasting.
- Class 10 Maths chapter 13 exercise 13.3 also covers the important concepts of exercise 13.2.
- Class 10 Maths chapter 13 exercise 13.3 also contains concepts related to time value for objects to be filled or empty.
Key Features For Class 10 Maths Chapter 13 Exercise 13.3
- Step-by-Step Solutions: Clear and detailed explanations for each problem in Ex 13.3 class 10, ensuring students understand the methodology.
- Conceptual Understanding: Explanation of surface area and volume concepts involved in the exercises, aiding students in grasping the underlying principles are discussed in class 10 maths ex 13.3.
- Variety of Problems: In class 10 ex 13.3, diverse types of problems, offering a broad spectrum of challenges to reinforce understanding.
- Visual Aids, Diagrams, and Examples: Use of visual representations, diagrams, and real-life examples to simplify complex concepts and aid visual learners.
- Application-Based Problems: In 10th class maths exercise 13.3 answers, application-oriented problems that relate statistics to real-world scenarios, fostering practical understanding and problem-solving skills.
Also, See:
NCERT Solutions Subject Wise
Popular Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
