Have you happened to see the beautiful shapes on a soap bubble or the fringe that looks like a rainbow on a CD? These effects are a result of the wave nature of the light. The NCERT Solutions for Class 12 Physics Chapter 10 Wave Optics describe these in an easy and logical way and include all the important topics such as Huygens' principle, interference, diffraction, and polarisation in a practical step-wise manner.
This Story also Contains
NCERT Solutions for Class 12 Physics Chapter 10: Download PDF
Class 12 Physics Chapter 10 Wave Optics: Exercises Questions
Wave Optics Class 12 NCERT Solutions: Additional Questions: Additional questions
Class 12 Physics NCERT Chapter 10: Higher Order Thinking Skills (HOTS) Questions
NCERT Wave Optics Class 12 Chapter 10 -Topics
NCERT Wave Optics Class 12 Chapter 10 - Important Formulas
Approach to Solve Questions of Wave Optics Class 12
What Extra Should Students Study Beyond NCERT for JEE/NEET?
NCERT Solutions for Class 12 Physics: Chapter-Wise
Also, check NCERT Books and NCERT Syllabus here:
NCERT Solution or Wave Optics
These solutions make it easier to comprehend tricky concepts and solve all exercise questions efficiently, created by expert faculty following the latest CBSE syllabus. These NCERT Solutions can be used during preparation for board exams and other competitive exams like JEE and NEET, as well as they also enable quick revision. The Wave Optics NCERT Solutions Class 12 Physics PDF is provided here so that students can study at their own times and places and reinforce their understanding of the concepts of wave optics.
NCERT Solutions for Class 12 Physics Chapter 10: Download PDF
The NCERT Solutions to Class 12 Physics Chapter 10 Wave Optics are a great way to make the learning process much simpler, as the chapter provides explanations of concepts such as interference, diffraction, polarisation, and the principle of Huygens. The PDF can be downloaded and used to revise quickly and prepare the solved exercise questions before the exams and competitive tests like JEE and NEET.
Aakash Repeater Courses
Take Aakash iACST and get instant scholarship on coaching programs.
Class 12 Physics Chapter 10 Wave Optics: Exercises Questions
Wave Optics Class 12 NCERT exercise questions cover important topics like interference, diffraction, and polarisation. These concepts help explain how light behaves as a wave. Below are the detailed NCERT solutions to help you understand and solve these questions easily.
Given a monochromatic light has a wavelength of $589 nm\ or\ 589\times 10^{-9}m$.
And as we know, the speed of light in air is, $c = 3\times 10^{8} m/s$.
Refractive index of water, $\mu = 1.33$
Therefore we have now,
The ray is incident on the medium, and then it gets reflected back to the same medium therefore, the wavelength, speed, and frequency will be the same as that of the incident ray.
We have the frequency of light is given by the relation,
$v = \frac{c}{\lambda}$
$= \frac{3\times 10^8 m/s}{589\times 10^{-9}}$
$= 5.09\times 10^{14}Hertz$ $
Therefore the speed, frequency, and wavelength of the reflected light are $3\times 10^{8} m/s$ , $5.09\times 10^{14}Hertz$ , and $589 nm$ respectively.
The wavelength of the monochromatic light $\lambda =589nm=589*10^{-9}m$
Refractive index of the water $\mu_{water}=1.33$
b)In the case of refraction, speed and wavelength will change as the medium is changing; however, the frequency will remain the same because it doesn't change when the medium is changed,
so, frequency $f=5.09 * 10^{14}Hz$
Speed of rays: speed of rays in water with refractive index 1.33 is
The shape of light emerging out of a convex lens when a point source is placed at its focus is Parallel .when light rays come from infinity parallelly, they intersect at focus of convex lens and hence when light is emerging from the focus, the rays will get parallel to each other after coming out of the convex lens, because path of light rays are reversible.
The portion of the wavefront of the light from the distant star which is seen from Earth is a plane since a small area of a large sphere will nearly look like a plane.
No, the speed of light in glass is not independent of the colour. The colour of the light does influence the refractive index and speed of light in the medium. The refractive index of the violet light is greater than the refractive index of red light and hence red component of the white light travels faster in the glass than the red component of the light.
as
$v=\frac{c}{\mu }$
The more the refractive index, the slower the speed.
Let the nth bright fringe due to wavelength, $\lambda_2$ and (n − 1) th bright fringe due to wavelength $\lambda_1$ coincide on the screen. We can equate the conditions for bright fringes as:
$n\lambda_2=(n-1)\lambda _1$
$520n=650n-650$
$650=130n$
$n=5$
Hence, the least distance from the central maximum can be obtained by the relation:
Wave Optics Class 12 NCERT Solutions: Additional Questions: Additional questions
Wave Optics Class 12 NCERT Solutions: Additional Questions include extra practice problems to boost your understanding. These questions are helpful for board exam revision and competitive exams like JEE and NEET.
According to corpuscular theory, when a corpuscle of light goes from a rare medium to a denser medium, the component of its velocity along the surface of the interface remains the same.
So we can write
$v_1sini=v_2sinr$
$\frac{v_2}{v_1}=\frac{sini}{sinr}=\mu$
As $\mu>1$ ,
$v_2>v_1$
That is, light should be faster in the dense medium than in the rare medium. This is the opposite of what we see experimentally.
Huygens' wave theory predicts that light is faster in a rare medium, which matches our experimental observation.
Let an object M be placed in front of a plane mirror AB at a distance r.
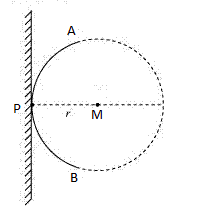
A circle is drawn from the centre, such that it just touches the plane mirror at point P. According to the Huygens’ principle, AB is the wavefront of the incident light.
If the mirror is absent, then a similar wavefront A'B' would form behind M at a distance r.
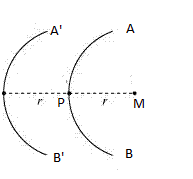
A'B' can be considered as a virtual reflected ray for the plane mirror. Hence a point object placed in front of the plane mirror produces an image at the same distance as the object.
The speed of light in any medium depends upon the wavelength of the light and does not depend on the nature of the source, direction of propagation, the motion of the source and/or observer, and intensity of the wave.
The sound wave requires a medium for propagation. So, even though both given situations may relate to the same relative motion, they are not identical physically since the motion of the observer, relative to the medium, is different in the two situations. Hence, we cannot expect the Doppler formula to be identical in both given cases.
When light waves are in a vacuum, there is clearly nothing to distinguish between two cases.
For light propagation in a medium, two situations are not identical for the same reason as in the case of sound waves.
the width of the central diffraction band is given by
$2D\frac{\lambda}{d}$
where d is the width of the slit.
So when we double the width of the slit, the size of the central diffraction band reduces to half of its value. But, the light amplitude becomes double, which increases the intensity 4 times.
When we have a width in the order of $\lambda$, the intensity of interference fringes in Young's double-slit experiment is modified by the diffraction pattern of each slit.
A bright spot is seen at the centre of the shadow of the obstacle because waves diffracted from the edge of a circular obstacle interfere constructively at the centre of the shadow, producing the bright spot.
The typical size of the obstacle is much larger than the wavelength of light. Hence the diffraction effect is negligibly small. Thus, the assumption that light travels in a straight line can be safely used in day-to-day life.
When a low-flying aircraft passes overhead, we notice slight shaking in the pictures on the TV. This is because aircraft interfere with signals and reflect them. So the shaking we see is the interference of the direct signal and the reflected signal.
The superposition principle comes from the linear character of the differential equation of wave motion. That is, if $x_1$ and $x_2$ are the solutions of any wave equation, then a linear combination of $x_1$ and $x_2$ is also the solution of the wave equation.
At this angle, each slit will make the first diffraction minimum. Therefore, the resultant intensity for all the slits will be zero at the angle of $\frac{n\lambda}{b}$.
Class 12 Physics NCERT Chapter 10: Higher Order Thinking Skills (HOTS) Questions
Class 12 Physics Chapter 10 Wave Optics HOTS Questions help students develop analytical and reasoning skills by applying concepts like interference, diffraction, and polarisation to solve complex problems. These questions are ideal for exam preparation and competitive exams like JEE and NEET, strengthening conceptual understanding.
Q1: In Young's Double Slit Experiment, the distance between the slits and the screen is 1.2m, and the distance between the two slits is 2.4 m. If a thin transparent mica sheet of thickness 1 µm and R.I. 1.5 is introduced between one of the interfering beams, the shift in the position of the central bright fringe is
Answer:
$
(\mu-1) t=\frac{x d}{D} \text { or } \mu=1+\frac{x d}{D t}
$
Or $x=\frac{(\mu-1) t D}{d}=\frac{(1.5-1) \times 1 \times 10^{-6} \times 1.2}{2.4 \times 10^{-3}}=0.25 \mathrm{~mm}$
Q2: Three polaroid sheets, P1, P2 and P3, are kept parallel to each other such that the angle between the pass axes of P1 and P2 is 45o and that between P2 and P3 is 45o. If an unpolarised beam of light of intensity 128 Wm-2 is incident on P1. What is the intensity of light coming out of P3?
Answer:
The ray of light passing through polaroid $P_1$ will have its intensity reduced by half.
$
I_1=\frac{I_0}{2}
$
Now, the polaroid $\mathrm{P}_2$ is oriented at an angle $45^{\circ}$ with respect to $\mathrm{P}_1$.
Therefore the intensity is $I_2=I_1 \cos ^2 45^{\circ}=\frac{I_0}{2} \times \frac{1}{2}=\frac{I_0}{4}$
Now, the polaroid $P_3$ is oriented at an angle $45^{\circ}$.
Therefore, the intensity is $I_3=I_2 \cos ^2 45^{\circ}=\frac{I_0}{4} \cos ^2 45^{\circ}=\frac{I_0}{4} \times \frac{1}{2}=\frac{I_0}{8}$
And given, $I_o=128 \mathrm{Wm}^{-2}$
So, $I_3=\frac{I_o}{8}=\frac{128}{8}=16 \mathrm{Wm}^{-2}$
interfere at a point, then the amplitude of the resultant wave is
Answer:
Resultant amplitude of two waves -
$
A=\sqrt{A_1^2+A_2^2+2 A_1 A_2 \cos \theta}
$
wherein
$A_1=$ amplitude of wave 1
$A_2=$ amplitude of wave 2
$\phi=$ phase difference
here $\phi=0$
$A=\sqrt{9+16+2 \times 3 \times 4 \times 1}$
$A=\sqrt{49}=7$
Q4: Maximum intensity in YDSE is $I_1$. The intensity at a point on the screen where the phase difference between the two interfering beams is $\frac{\pi}{3}$:
Q5: Figure 10.2 shows a standard two-slit arrangement with slits S1, S2. P1 and P2 are the two minima points on either side of P (Fig. 10.2). At P2 on the screen, there is a hole and behind P2 is a second 2-slit arrangement with slits S3, S4 and a second screen behind them.
Answer: In the given figure, there is a hole atthe minima point $P_2$, the hole will act as a source of fresh light for the slits $\mathrm{S}_3$ and $\mathrm{S}_4$. Hence, there will be a regular two slit pattern on the second screen.
CBSE Class 12th Syllabus: Subjects & Chapters
Select your preferred subject to view the chapters
Class 12 Physics Chapter 10 Wave Optics explains the wave nature of light and its behaviour in different scenarios. The topics cover concepts like Huygens’ principle, interference, diffraction, and polarisation, helping students understand how light waves interact and propagate in various mediums.
NCERT Wave Optics Class 12 Chapter 10 - Important Formulas
All the important formulas of wave optics are presented here, saving the students the trouble of referring to a large number of books to revise. It provides formulas that are needed to solve interference, diffraction, polarisation, and fringe calculations, needed to solve NCERT problems, as well as competitive exams such as JEE and NEET.
where $\lambda=$ wavelength of light, $D=$ distance between slits and screen, $d=$ distance between slits.
2. Diffraction of Light
- Width of central maximum for single slit:
$
w=\frac{2 \lambda L}{a}
$
where $a=$ slit width, $L=$ distance to screen.
- Condition for minima in single slit diffraction:
$
a \sin \theta=m \lambda \quad(m=1,2,3, \ldots)
$
3. Polarisation of Light
- Malus' Law:
$
I=I_0 \cos ^2 \theta
$
where $I_0=$ initial intensity, $\theta=$ angle between light's polarisation and polariser axis.
4. Thin Films (Interference)
- Condition for constructive interference (reflection):
$
2 n t=m \lambda \quad(\text { or }(2 m+1) \lambda / 2 \text { depending on phase change })
$
where $n=$ refractive index of film, $t=$ thickness of film, $m=0,1,2 \ldots$.
- Condition for destructive interference (reflection):
$
2 n t=\left(m+\frac{1}{2}\right) \lambda
$
Approach to Solve Questions of Wave Optics Class 12
Students should follow a step-wise approach to solve Wave Optics questions in Class 12 Physics. Identify the phenomenon involved first: is it the interference, diffraction or polarisation? In the case of interference (such as in the case of Young's slit interference experiment), focus on the path difference and then apply the condition of constructive or destructive interference with the use of the fringe width formula. In diffraction problems, find a connection between slit width, wavelength and angle using the minimum condition and find the width of the central maximum. In the case of polarisation, use Malus' law and note the place of the polariser and analyser. Every time you write the values, use the correct formula and replace values with appropriate units. Finally, make neat drawings when possible, as they would help to make a visual image of the wave behaviour and reduce errors in the calculation.
What Extra Should Students Study Beyond NCERT for JEE/NEET?
Beyond NCERT, students preparing for JEE/NEET Wave Optics should focus on advanced problem-solving and tricky applications of concepts like interference, diffraction, and polarisation. Extra study should include topics such as intensity distribution in interference and diffraction patterns, Brewster’s law in detail, resolving power of optical instruments, and numerical problems combining ray optics with wave optics. Practising previous years’ JEE/NEET questions will also strengthen conceptual clarity and speed.
Q: Is the Wave Optics Class 12 NCERT PDF enough for board exam preparation?
A:
Yes, the Wave Optics Class 12 NCERT PDF covers all important concepts and questions. It’s a must for board exam prep and builds your foundation for competitive exams like JEE and NEET.
Q: Are there any Wave Optics questions with answers PDF for practice?
A:
You can download Wave Optics questions with answers PDF for extra practice. These help you solve different types of questions from exams and strengthen your understanding.
Q: What do Class 12 Physics Chapter 11 Exercise Solutions include?
A:
Class 12 Physics Chapter 11 Exercise Solutions include detailed answers to all NCERT textbook questions, along with step-by-step explanations for better understanding.
Q: How can I quickly solve the wave optics-based problems in Chapter 10 of wave optics class 12 ncert?
A:
To quickly solve ncert wave optics problems in ch 10 physics class 12, make sure you have a clear understanding of the fundamental concepts and practice solving problems. Read the problem statement carefully and use diagrams to visualize the problem. Review your work and seek help if needed.
Q: Are NCERT books for Class 12 Physics enough to prepare for CBSE Board exams?
A:
Yes, NCERT books are enough to prepare for the board exams, but you can refer to other reference books and sample papers as well. Try to cover all the concepts based on the NCERT syllabus. To get a good score in the CBSE board exam understand all the topics in the NCERT book and solve all the questions of NCERT exercise. Additionally students can refer NCERT exemplar problems and CBSE previous year question papers.
If you want to improve the Class 12 PCM results, you can appear in the improvement exam. This exam will help you to retake one or more subjects to achieve a better score. You should check the official website for details and the deadline of this exam.
SASTRA University commonly provides concessions and scholarships based on merit in class 12 board exams and JEE Main purposes with regard to board merit you need above 95% in PCM (or on aggregate) to get bigger concessions, usually if you scored 90% and above you may get partial concessions. I suppose the exact cut offs may change yearly on application rates too.
CBSE generally forwards the marksheet for the supplementary exam to the correspondence address as identified in the supplementary exam application form. It is not sent to the address indicated in the main exam form. Addresses that differ will use the supplementary exam address.
To find Class 12 Arts board papers, go to the official website of your education board, then click on the Sample Papers, Previous Years Question Papers(PYQ) or Model Papers section, and select the Arts stream. You will find papers for the various academic year. You can then select the year of which you want to solve and do your practice. There are many other educational websites that post pyqs on their website you can also visit that.
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g = 9.8 ms−2 :
A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is
