NCERT Solutions for Class 12 Physics Chapter 4 - Moving Charges and Magnetism

Q: What is the weightage of NCERT physics chapter 4 for CBSE board exam

The chapter Moving Charges and Magnetism have 8 to 10 percentage weightage. The questions asked from the chapter can be of a numerical, derivation or theory questions. CBSE board follows NCERT Syllabus. To practice problems refer to NCERT text book, NCERT syllabus and previous year board papers of Class 12 Physics.

Q: Can I skip the chapter moving charges for NEET preperation

No, you can not skip it. Since from NCERT Class 12 Physics chapter 4 you can expect 2 questions for NEET exam.

Q: Can I crack JEE Main questions from Moving Charges and Magnetism just by knowing the equations in the NCERT

No, you have to practise more questions for doing well in JEE main exams. The questions of Moving Charges and Magnetism need a good base of vectors and a thorough understanding of concepts

Vishal kumarUpdated on 20 Aug 2025, 01:04 PM IST

The NCERT solutions provide step-by-step explanations for all the problems in Chapter 4, helping you understand the application of laws. With the help of the NCERT solution for Class 12 Physics, students may ensure that they have a solid understanding of the concepts presented in each chapter and prepare for tests such as JEE Main, NEET and CBSE Class 12.

This Story also Contains

NCERT Solutions for Class 12 Physics Chapter 4: Download PDF
NCERT Solutions for Class 12 Physics Chapter 4: Exercise Questions
NCERT Solutions for Class 12 Physics Chapter 4: Additional Questions
Class 12 Physics NCERT Chapter 4: Higher Order Thinking Skills (HOTS) Questions
NCERT Class 12 Physics Moving charges and Mangetism: Topics
Class 12 Physics Chapter 4 Exercise solutions: Important Formulas
Approach to Solve Questions of Moving Charge and Magnetism Class 12
What Extra Should Students Study Beyond the NCERT for JEE/NEET?
Importance in Exams:
NCERT Solutions for Class 12 Physics: Chapter-Wise

Moving charge

The NCERT solutions include solved exercise questions, additional questions and HOTS, or higher order thinking skills questions, to create higher order problem solving skills, important Topics and formulas of magnetic fields, Biot-Savart Law, Ampere Circuital Law, force on current carrying conductor, and magnetic field due to a current loop and approach to solve questions.

The important topics in Class 12 Physics Chapter 4, Moving Charges and Magnetism, are the Lorentz Force and the Motion of a Charged Particle, Biot-Savart Law and its Applications, Ampere's Circuital Law and its Applications, Force Between Two Parallel Current-Carrying Wires, and Moving Coil Galvanometer

Aakash Repeater Courses

Take Aakash iACST and get instant scholarship on coaching programs.

Apply

NCERT Solutions for Class 12 Physics Chapter 4: Download PDF

You will find complete step-by-step solutions of NCERT Class 12 Physics Chapter 4 – Moving Charges and Magnetism. Get the free PDF from us to enhance your knowledge base and improve your test performance.

Download PDF

NCERT Solutions for Class 12 Physics Chapter 4: Exercise Questions

4.1 A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil?

Answer :

The magnitude of the magnetic field at the centre of a circular coil of radius r carrying current I is given by,

$| B | = \frac{μ_{0} I}{2 r}$

For 100 turns, the magnitude of the magnetic field will be,

$| B | = 100 \times \frac{μ_{0} I}{2 r}$

(Given, current=0.4A, radius = 0.08m, permeability of free space = 4 $π \times$ 10 -7 TmA^-1)

$| B | = 100 \times \frac{4 π \times 10^{- 7} \times 0.4}{2 \times 0.08} = 3.14 \times 10^{- 4} T$

4.2 A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire?

Answer:

The magnitude of the magnetic field at a distance r from a long straight wire carrying current I is given by,

$| B | = \frac{μ_{0} I}{2 π r}$

In this case

(Given, current=0.4A, radius = 0.08m, permeability of free space = 4 $π \times$ 10 -7 TmA^-1)

$| B | = \frac{4 π \times 10^{- 7} \times 35}{2 π \times 0.2} = 3.5 \times 10^{- 5} T$

4.3 A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.

Answer:

The magnitude of the magnetic field at a distance r from a long straight wire carrying current I is given by,

$| B | = \frac{μ_{0} I}{2 π r}$

In this case

(Given, current=0.4A, radius = 0.08m, permeability of free space = 4 $π \times$ 10 -7 TmA^-1)

$| B | = \frac{4 π \times 10^{- 7} \times 50}{2 π \times 2.5} = 4 \times 10^{- 6} T$

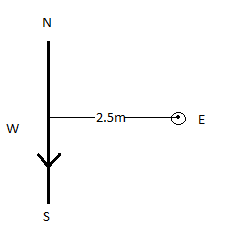
1643264249758

The current is going from the North to South direction in the horizontal plane and the point lies to the East of the wire. Applying Maxwell's right-hand thumb rule we can see that the direction of the magnetic field will be vertically upwards.

4.4 A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?

Answer:

The magnitude of the magnetic field at a distance r from a long straight wire carrying current I is given by,

$| B | = \frac{μ_{0} I}{2 π r}$

In this case

(Given, current=0.4A, radius = 0.08m, permeability of free space = 4 $π \times$ 10 -7 TmA^-1)

$| B | = \frac{4 π \times 10^{- 7} \times 90}{2 π \times 1.5} = 1.2 \times 10^{- 5} T$

The current in the overhead power line is going from the East to West direction and the point lies below the power line. Applying Maxwell's right-hand thumb rule we can see that the direction of the magnetic field will be towards the South.

4.5 What is the magnitude of magnetic force per unit length on a wire carrying a current of 8 A and making an angle of $30^{\circ}$ with the direction of a uniform magnetic field of 0.15 T?

Answer:

The magnetic force on an infinitesimal current-carrying conductor in a magnetic field is given by $\vec{d F} = I \vec{d l} \times \vec{B}$ where the direction of vector dl is in the direction of flow of current.

For a straight wire of length l in a uniform magnetic field, the Force equals to

$\vec{F} = \int_{0}^{l} I \vec{d l} \times \vec{B} | \vec{F} | = B I l s i n θ$

In the given case the magnitude of force per unit length is equal to

(Given, I=8A, B=0.15 T, $θ$ =30^o)

|F| = 0.15 $\times$ 8 $\times$ sin30^o =0.6 Nm^-1

4.6 A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?

Answer:

For a straight wire of length l in a uniform magnetic field, the Force equals to

$\vec{F} = \int_{0}^{l} I \vec{d l} \times \vec{B}$

$\Rightarrow | \vec{F} | = B I l s i n θ$

In the given case the magnitude of the force is equal to

(Given, I=10A, B=0.27 T, $θ$ =90^o)

|F| = 0.27 $\times$ 10 $\times$ 0.03 $\times$ sin90^o =0.081 N

The direction of this force depends on the orientation of the coil and the current-carrying wire and can be known using the Flemings Left-hand rule.

4.7 Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.

Answer:

The magnitude of magnetic field at a distance r from a long straight wire carrying current I is given by,

$| B | = \frac{μ_{0} I}{2 π r}$

In this case the magnetic field at a distance of 4.0 cm from wire B will be

(Given, I=5 A, r=4.0 cm)

$| B | = \frac{4 π \times 10^{- 7} \times 5}{2 π \times 0.04} = 2.5 \times 10^{- 5} T$

The force on a straight wire of length l carrying current I in a uniform magnetic field B is given by

$F = B I l s i n θ$ , where $θ$ is the angle between the direction of flow of current and the magnetic field.

The force on a 10 cm section of wire A will be

(Given, B=2.5 T, I=8 A, l = 10 cm, $θ$ =90^o)

$F = 2.5 \times 10^{- 5} \times 8 \times 0.1 \times s i n 90^{\circ}$

$F = 2 \times 10^{- 5} N$

4.8 A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.

Answer:

The magnitude of the magnetic field at the centre of a solenoid of length $ℓ$ , total turns N and carrying current I is given by

$B = \frac{μ_{o} N I}{l}$ , where $μ_{o}$ is the permeability of free space.

In the given question N= number of layers of winding $\times$ number of turns per each winding

N=5 $\times$ 400=2000

I=8.0 A

$ℓ = 80 c m$

$B = \frac{4 π \times 10^{- 7} \times 2000 \times 8}{0.8}$

$B = 2.51 \times 10^{- 2} T$

4.9 A square coil of side 10 cm consists of 20 turns and carries a current of 12 A. The coil is suspended vertically and the normal to the plane of the coil makes an angle of $30^{\circ}$ with the direction of a uniform horizontal magnetic field of magnitude 0.80 T. What is the magnitude of torque experienced by the coil?

Answer:

The magnitude of torque experienced by a current-carrying coil in a magnetic field is given by

$τ = n B I A s i n θ$

where n = number of turns, I is the current in the coil, A is the area of the coil and $θ$ is the angle between the magnetic field and the vector normal to the plane of the coil.

In the given question n = 20, B=0.8 T, A=0.1 $\times$ 0.1=0.01 m² , I=12 A, $θ$ =30^o

$τ = 20 \times 0.8 \times 12 \times 0.01 \times s i n 30^{o} = 0.96 N m$

The coil, therefore, experiences a torque of magnitude 0.96 Nm.

4.10 (a) Two moving coil meters, $M_{1}$ and $M_{2}$ have the following particulars:
$R_{1} = 10 Ω, N_{1} = 30, A_{1} = 3.6 \times 10^{- 3} m^{2}, B_{1} = 0.25 T$ $R_{2} = 14 Ω, N_{2} = 42, A_{2} = 1.8 \times 10^{- 3} m^{2}, B_{2} = 0.50 T$
(The spring constants are identical for the two meters).
Determine the ratio of current sensitivity of $M_{2} a n d M_{1}$

Answer:

The torque experienced by the moving coil M₁ for a current I passing through it will be equal to $τ = B_{1} A_{1} N_{1} I$

The coil will experience a restoring torque proportional to the twist $ϕ$

$ϕ k = B_{1} A_{1} N_{1} I$

The current sensitivity is therefore $\frac{B_{1} A_{1} N_{1}}{k}$

Similarly, for the coil M₂, current sensitivity is $\frac{B_{2} A_{2} N_{2}}{k}$

Their ratio of current sensitivity of coil M₂ to that of coil M₁ is, therefore,

$\frac{B_{2} A_{2} N_{2}}{B_{1} A_{1} N_{1}} = \frac{0.5 \times 1.8 \times 10^{- 3} \times 42}{0.25 \times 3.6 \times 10^{- 3} \times 30} = 1.4$

4.10(b) Two moving coil meters, $M_{1}$ and $M_{2}$ have the following particulars:

$R_{1} = 10 Ω, N_{1} = 30, A_{1} = 3.6 \times 10^{- 3} m^{2}, B_{1} = 0.25 T$ $R_{2} = 14 Ω, N_{2} = 42, A_{2} = 1.8 \times 10^{- 3} m^{2}, B_{2} = 0.50 T$
(The spring constants are identical for the two meters).

Determine the ratio of voltage sensitivity of $M_{2}$ and $M_{1}$

Answer:

The torque experienced by the moving coil M₁ for a current I passing through it will be equal to $τ = B_{1} A_{1} N_{1} I$

The coil will experience a restoring torque proportional to the twist $ϕ$

$ϕ k = B_{1} A_{1} N_{1} I$

we know V=IR

Therefore, $ϕ k = \frac{B_{1} A_{1} N_{1} V}{R_{1}}$

Voltage sensitivity of coil M₁ = $\frac{B_{1} A_{1} N_{1}}{k R_{1}}$

Similarly for coil M₂ Voltage sensitivity = $\frac{B_{2} A_{2} N_{2}}{k R_{2}}$

Their ratio of voltage sensitivity of coil M₂ to that of coil M₁ is:

$\frac{B_{2} A_{2} N_{2} R_{1}}{B_{1} A_{1} N_{1} R_{2}} = 1.4 \times \frac{10}{14} = 1$

4.11 In a chamber, a uniform magnetic field of $6.5 G (1 G = 10^{- 4} T)$ is maintained. An electron is shot into the field with a speed of $4.8 \times 10^{6} m s^{- 1}$ normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit. $(e = 1.5 \times 10^{- 19} C, m_{e} = 9.1 \times 10^{- 31} k g)$

Answer:

The magnetic force on a moving charged particle in a magnetic field is given by $\vec{F_{B}} = q \vec{v} \times \vec{B}$

Since the velocity of the shot electron is perpendicular to the magnetic field, there is no component of velocity along the magnetic field and therefore the only force on the electron will be due to the magnetic field and will be acting as a centripetal force causing the electron to move in a circular path. (if the initial velocity of the electron had a component along the direction of the magnetic field it would have moved in a helical path)

Magnetic field(B)= $6.5 G (1 G = 10^{- 4} T)$

Speed of electron(v)= $4.8 \times 10^{6} m s^{- 1}$

Charge of electron= $- 1.6 \times 10^{- 19} C$

Mass of electron= $9.1 \times 10^{- 31} k g$

The angle between the direction of velocity and the magnetic field = 90^o

Since the force due to the magnetic field is the only force acting on the particle,

$\frac{m v^{2}}{r} = q \vec{v} \times \vec{B}$

$\frac{m v^{2}}{r} = | q v B s i n θ |$

$r = | \frac{m v}{q B s i n θ} |$

$r = \frac{9.1 \times 10^{- 31} \times 4.8 \times 10^{6}}{1.6 \times 10^{- 19} \times 6.5 \times 10^{- 4}} = 4.2 c m$

4.12 In Exercise 4.11 obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain

Answer:

In exercise 4.11 we saw $r = \frac{e B}{m v}$

Time taken in covering the circular path once(time period (T))= $\frac{2 π r}{v} = \frac{2 π m}{e B}$

Frequency, $ν = \frac{1}{T} = \frac{e B}{2 π m}$

From the above equation, we can see that this frequency is independent of the speed of the electron.

$ν = \frac{1.6 \times 10^{- 19} \times 4.8 \times 10^{6}}{2 π \times 9.1 \times 10^{- 31}} = 18.2 M H z$

4.13 (a) A circular coil of 30 turns and radius 8.0 cm carrying a current of 6.0 A is suspended vertically in a uniform horizontal magnetic field of magnitude 1.0 T. The field lines make an angle of $60^{\circ}$ with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning.

Answer:

Number of turns in the coil(n)=30

The radius of the circular coil(r)=8.0 cm

Current flowing through the coil=6.0 A

Strength of magnetic field=1.0 T

The angle between the field lines and the normal of the coil=60^o

The magnitude of the counter-torque that must be applied to prevent the coil from turning would be equal to the magnitude of the torque acting on the coil due to the magnetic field.

$τ = n B I A \sin θ$

$τ = 30 \times 1 \times 6 \times π \times (0.08)^{2} \times \sin 60^{o} = 3.13 Nm$

A torque of magnitude 3.13 Nm must be applied to prevent the coil from turning.

4.13 (b) Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.)

Answer:

From the relation $τ = n B I A \sin θ$ we can see that the torque acting on the coil depends only on the area and not its shape, therefore, the answer won't change if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area.

NCERT Solutions for Class 12 Physics Chapter 4: Additional Questions

1) Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.

Answer:

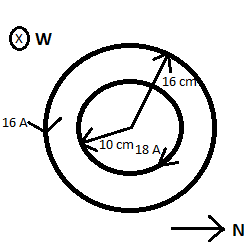
1643264303579

Using the right-hand thumb rule we can see that the direction of the magnetic field due to coil X will be towards the east direction and that due to coil Y will be in the West direction.

We know the magnetic field at the centre of a circular loop of radius r carrying current I is given by

$B = \frac{μ_{o} I}{2 r}$

$B_{x} = \frac{n_{x} μ_{o} I_{x}}{2 r_{x}}$

$B_{x} = \frac{20 \times 4 π \times 10^{- 7} \times 16}{2 \times 0.16}$

$B_{x} = 4 π \times 10^{- 4} T$ (towards East)

$B_{y} = \frac{n_{y} μ_{o} I_{y}}{2 r_{y}}$

$B_{y} = \frac{25 \times 4 π \times 10^{- 7} \times 18}{2 \times 0.1}$

$B_{y} = 9 π \times 10^{- 4} T$ (towards west)

The net magnetic field at the centre of the coils,

B_net =B_y - B_x =1.57 $\times$ 10^-3 T

The direction of the magnetic field at the centre of the coils is towards the west direction.

2) A magnetic field of $100 G (1 G = 10^{- 4}) T$ is required which is uniform in a region of linear dimension about 10 cm and area of cross-section about $10^{- 3} m^{2}$ The maximum current-carrying capacity of a given coil of wire is 15 A and the number of turns per unit length that can be wound round a core is at most $1000 t u r n s m^{- 1}$ . Suggest some appropriate design particulars of a solenoid for the required purpose. Assume the core is not ferromagnetic.

Answer:

Strength of the magnetic field required is $100 G (1 G = 10^{- 4}) T$

$B = μ_{o} n I$

$n I = \frac{B}{μ_{o}}$

$n I = \frac{100 \times 10^{- 4}}{4 π \times 10^{- 7}} = 7957.74 \approx 8000$

Therefore keeping the number of turns per unit length and the value of current within the prescribed limits such that their product is approximately 8000 we can produce the required magnetic field.

e.g. n=800 and I=10 A.

3) For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

$B = \frac{μ_{0} I R^{2} N}{2 (x^{2} + R^{2})^{3 / 2}}$

Show that this reduces to the familiar result for the field at the centre of the coil.

Answer:

For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

$B = \frac{μ_{0} I R^{2} N}{2 (x^{2} + R^{2})^{3 / 2}}$

For finding the field at the centre of coil we put x=0 and get the familiar result

$B = \frac{μ_{0} I N}{2 R}$

4) For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

$B = \frac{μ_{0} I R^{2} N}{2 (x^{2} + R^{2})^{3 / 2}}$

Consider two parallel co-axial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R, and is given by,
$B = 0.72 \frac{μ_{0} N I}{R}$ approximately.

Answer:

Let a point P be at a distance of l from the midpoint of the centres of the coils.

The distance of this point from the centre of one coil would be $R / 2 + l$ and that from the other would be $R / 2 - l$ .

The magnetic field at P due to one of the coils would be

$B_{1} = \frac{μ_{0} I R^{2} N}{2 ((R / 2 + l)^{2} + R^{2})^{3 / 2}}$

The magnetic field at P due to the other coil would be

$B_{2} = \frac{μ_{0} I R^{2} N}{2 ((R / 2 - l)^{2} + R^{2})^{3 / 2}}$

Since the direction of current in both the coils is same the magnetic fields B₁ and B₂ due to them at point P would be in the same direction

$\begin{aligned} B_{net} = B_{2} + B_{1} \\ B_{n e t} = \frac{μ_{0} I R^{2} N}{2 {((R / 2 - l)^{2} + R^{2})}^{3 / 2}} + \frac{μ_{0} I R^{2} N}{2 {((R / 2 + l)^{2} + R^{2})}^{3 / 2}} \\ B_{n e t} = \frac{μ_{0} I R^{2} N}{2} [{((R / 2 - l)^{2} + R^{2})}^{- 3 / 2} + {((R / 2 + l)^{2} + R^{2})}^{- 3 / 2}] \\ B_{n e t} = \frac{μ_{0} I R^{2} N}{2} [{(\frac{R^{2}}{4} - R l + l^{2} + R^{2})}^{- 3 / 2} + {(\frac{R^{2}}{4} + R l + l^{2} + R^{2})}^{- 3 / 2}] \\ B_{n e t} = \frac{μ_{0} I R^{2} N}{2} [{(\frac{5 R^{2}}{4} - R l + l^{2})}^{- 3 / 2} + {(\frac{5 R^{2}}{4} + R l + l^{2})}^{- 3 / 2}] \\ B_{n e t} = \frac{μ_{0} I R^{2} N}{2} \times {(\frac{5 R^{2}}{4})}^{- 3 / 2} [{(1 - \frac{4 l}{5 R} + \frac{4 l^{2}}{5 R^{2}})}^{- 3 / 2} + {(1 + \frac{4 l}{5 R} + \frac{4 l^{2}}{5 R^{2}})}^{- 3 / 2}] \end{aligned}$

Since $l << R$ we can ignore term $l² /R²

$B_{n e t} = \frac{μ_{0} I N}{2 R} \times (\frac{5}{4})^{- 3 / 2} [(1 - \frac{4 l}{5 R})^{- 3 / 2} + (1 + \frac{4 l}{5 R})^{- 3 / 2}]$

$B_{n e t} = \frac{μ_{0} I N}{2 R} \times (\frac{4}{5})^{3 / 2} [1 + \frac{6 l}{5 R} + 1 - \frac{6 l}{5 R}]$

$B_{n e t} = \frac{μ_{0} I N}{2 R} \times (\frac{4}{5})^{3 / 2} \times 2$

$B_{n e t} = 0.715 \frac{μ_{0} I N}{R} \approx 0.72 \frac{μ_{0} I N}{R}$

Since the above value is independent of $l$ for small values it is proved that about the midpoint the Magnetic field is uniform.

5(a) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field outside the toroid

Answer:

Outside the toroid, the magnetic field will be zero.

5(b) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field inside the core of the toroid?

Answer:

The magnetic field inside the core of a toroid is given by

$B = \frac{μ_{o} N I}{l}$

Total number of turns(N)=3500

Current flowing in toroid =11 A

Length of the toroid,

$\begin{aligned} l = 2 π (\frac{r_{1} + r_{2}}{2}) \\ l = π (r_{1} + r_{2}) (r_{1} = inner radius = 25 cm, r_{2} = outer radius = 26 cm) \\ l = π (0.25 + 0.26) \\ l = 0.51 π \end{aligned}$

$B = \frac{4 π \times 10^{- 7} \times 3500 \times 11}{0.51 π} = 0.031 T$

5(c) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field in the empty space surrounded by the toroid?

Answer:

The magnetic field in the empty space surrounded by the toroid is zero.

6(a) A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?

Answer:

The charged particle is not deflected by the magnetic field even while having a non zero velocity, therefore, its initial velocity must be either parallel or anti-parallel to the magnetic field i.e. It's velocity is either towards the east or the west direction.

6(b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?

Answer:

Yes, its final speed will be equal to the initial speed if it has not undergone any collision as the work done by the magnetic field on a charged particle is always zero because it acts perpendicular to the velocity of the particle.

6(c) An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.

Answer:

The electron would experience an electrostatic force towards the north direction, therefore, to nullify its force due to the magnetic field must be acting on the electron towards the south direction. By using Fleming's left-hand rule we can see that the force will be in the north direction if the magnetic field is in the vertically downward direction.

Explanation:

The electron is moving towards the east and has a negative charge therefore $\vec{v}$ is towards the west direction, Force will be towards south direction if the magnetic field is in the vertically downward direction as $\vec{F} = q \vec{v} \times \vec{B}$

7(a) An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field is transverse to its initial velocity

Answer:

The electron has been accelerated through a potential difference of 2.0 kV .

Therefore K.E of electron $= 1.6 \times 10^{- 19} \times 2000 = 3.2 \times 10^{- 16} J$

$\begin{aligned} \frac{1}{2} m v^{2} = 3.2 \times 10^{- 16} \\ v = \sqrt{\frac{2 \times 3.2 \times 10^{- 16}}{9.1 \times 10^{- 31}}} \\ v = 2.67 \times 10^{7} {ms}^{- 1} \end{aligned}$

Since the electron initially has velocity perpendicular to the magnetic field it will move in a circular path.
The magnetic field acts as a centripetal force. Therefore,

$\begin{aligned} \frac{m v^{2}}{r} = e v B \\ r = \frac{m v}{e B} \\ r = \frac{9.1 \times 10^{- 31} \times 2.67 \times 10^{7}}{1.6 \times 10^{- 19} \times 0.15} = 1.01 mm \end{aligned}$

7(b) An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field makes an angle of $30^{\circ}$ with the initial velocity.

Answer:

The electron has been accelerated through a potential difference of 2.0 kV .
Therefore K.E of electron $= 1.6 \times 10^{- 19} \times 2000 = 3.2 \times 10^{- 16} J$

$\begin{aligned} \frac{1}{2} m v^{2} = 3.2 \times 10^{- 16} \\ v = \sqrt{\frac{2 \times 3.2 \times 10^{- 16}}{9.1 \times 10^{- 31}}} \\ v = 2.67 \times 10^{7} {ms}^{- 1} \end{aligned}$

The component of velocity perpendicular to the magnetic field is

$\begin{aligned} v_{p} = v \sin 30^{\circ} \\ v_{p} = 1.33 \times 10^{7} {ms}^{- 1} \end{aligned}$

The electron will move in a helical path of radius r given by the relation,

$\begin{aligned} \frac{m v_{p}^{2}}{r} = e v_{p} B \\ r = \frac{m v_{p}}{e B} \\ r = \frac{9.1 \times 10^{- 31} \times 1.33 \times 10^{7}}{1.6 \times 10^{- 19} \times 0.15} \\ r = 5 m \\ r = 5 \times 10^{- 4} m \\ r = 0.5 mm \end{aligned}$

The component of velocity along the magnetic field is

$\begin{aligned} v_{t} = v \cos 30^{\circ} \\ v_{t} = 2.31 \times 10^{7} {ms}^{- 1} \end{aligned}$

The electron will move in a helical path of pitch p given by the relation,

$\begin{aligned} p = \frac{2 π r}{v_{p}} \times v_{t} \\ p = \frac{2 π \times 5 \times 10^{- 4}}{1.33 \times 10^{7}} \times 2.31 \times 10^{7} \\ p = 5.45 \times 10^{- 3} m \\ p = 5.45 mm \end{aligned}$

The electron will, therefore, move in a helical path of radius 5 mm and pitch 5.45 mm.

8. A magnetic field set up using Helmholtz coils (described in Q.3) is uniform in a small region and has a magnitude of 0.75 T. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through 15 kV enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is $9.0 \times 10^{- 5} V m^{- 1}$ , make a simple guess as to what the beam contains. Why is the answer not unique?

Answer:

$\begin{aligned} q E = q v B \\ E = v B \dots (i) \end{aligned}$

Let the beam consist of particles having charge q and mass m.
After being accelerated through a potential difference $V$ its velocity can be found out by using the following relation,

$\begin{aligned} \frac{1}{2} m v^{2} = q V \\ v = \sqrt{\frac{2 q V}{m}} \dots (i i) \end{aligned}$

Using the value of $v$ from equation (ii) in (i) we have

$\begin{aligned} E & = B \sqrt{\frac{2 q V}{m}} \\ \frac{q}{m} & = \frac{E^{2}}{2 V B^{2}} \\ \frac{q}{m} & = \frac{{(9 \times 10^{- 5})}^{2}}{2 \times 15 \times 10^{3} \times (0.75)^{2}} = 4.8 \times 10^{- 13} \end{aligned}$

9(a) A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?

Answer:

In order for the tension in the wires to be zero the force due to the magnetic field must be equal to the gravitational force on the rod.

$m g = B I l$

mass of rod=0.06 g

length of rod=0.45m

the current flowing through the rod=5 A

$B = \frac{m g}{I l}$

$B = \frac{0.06 \times 9.8}{5 \times 0.45}$

$B = 0.261 T$

A magnetic field of strength 0.261 T should be set up normal to the conductor in order that the tension in the wires is zero

9(b) A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before?
(Ignore the mass of the wires.) $g = 9.8 m s^{- 2}$

Answer:

If the direction of the current is reversed the magnetic force would act in the same direction as that of gravity.

Total tension in wires(T)=Gravitational force on rod + Magnetic force on rod

$\begin{aligned} T = m g + B I l \\ T = 0.06 \times 9.8 + 0.261 \times 5 \times 0.45 \\ T = 1.176 N \end{aligned}$

The total tension in the wires will be 1.176 N.

10. The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?

Answer:

Since the distance between the wires is much smaller than the length of the wires we can calculate the Force per unit length on the wires using the following relation.

$F = \frac{μ_{o} I_{1} I_{2}}{2 π d}$

Current in both wires=300 A

Distance between the wires=1.5 cm

Permeability of free space=4 $π \times$ 10^-7 TmA^-1

$F = \frac{4 π \times 10^{- 7} \times 300 \times 300}{2 π \times 0.015}$

F=1.2 Nm^-1

11.(a) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire intersects the axis?

Answer:

The length of wire inside the magnetic field is equal to the diameter of the cylindrical region=20.0 cm=0.2 m.

Magnetic field strenth=1.5 T.

Current flowing through the wire=7.0 A

The angle between the direction of the current and magnetic field=90^o

Force on a wire in a magnetic field is calculated by relation,

$F = B I l \sin θ$

$F = 1.5 \times 7 \times 0.2$

F=2.1 N

This force due to the magnetic field inside the cylindrical region acts on the wire in the vertically downward direction.

11.(b) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire is turned from N-S to northeast-northwest direction?

Answer:

Magnetic field strenth=1.5 T.

Current flowing through the wire=7.0 A

The angle between the direction of the current and magnetic field=45^o

The radius of the cylindrical region=10.0 cm

The length of wire inside the magnetic field, $l = \frac{2 r}{s i n θ}$

Force on a wire in a magnetic field is calculated by relation,

$F = B I l \sin θ$

$F = 1.5 \times 7 \times \frac{2 \times 0.1}{s i n 45^{o}} \times s i n 45^{o}$

F=2.1 N

This force due to the magnetic field inside the cylindrical region acts on the wire in the vertically downward direction.

This force will be independent of the angle between the wire and the magnetic field as we can see in the above case.

Note: There is one case in which the force will be zero and that will happen when the wire is kept along the axis of the cylindrical region.

11 (c) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?

Answer:

The wire is lowered by a distance d=6cm.

In this case, the length of the wire inside the cylindrical region decreases.

Let this length be $l$ .

$\begin{aligned} {(\frac{l}{2})}^{2} + d^{2} = r^{2} \\ {(\frac{l}{2})}^{2} = {0.1}^{2} - {0.06}^{2} \\ {(\frac{l}{2})}^{2} = 0.01 - 0.0036 \\ {(\frac{l}{2})}^{2} = 0.0064 \\ \frac{l}{2} = 0.08 \\ l = 0.16 m \\ F = B I l \sin θ \\ F = 1.5 \times 7 \times 0.16 \\ F = 1.68 N \end{aligned}$

This force acts in the vertically downward direction.

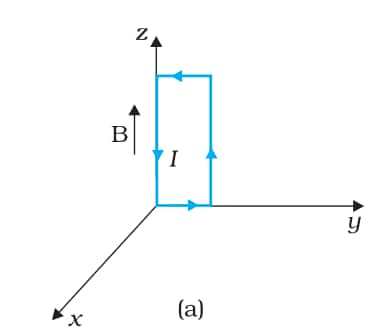
12.(a) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig? What is the force on each case? Which case corresponds to stable equilibrium?

Answer:

The magnetic field is

$\vec{B} = 3000 G \hat{k} = 0.3 T \hat{k}$

Current in the loop=12 A

Area of the loop = length $\times$ breadth

A=0.1 $\times$ 0.05

A=0.005 m²

$\vec{A} = 0.005 m^{2} \hat{i}$

Torque is given by,

$\begin{aligned} \vec{τ} = I \vec{A} \times \vec{B} \\ \vec{τ} = 12 \times 0.005 \hat{i} \times 0.3 \hat{k} \\ \vec{τ} = - 0.018 \hat{j} \end{aligned}$

The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-y direction. The force on the loop is zero.

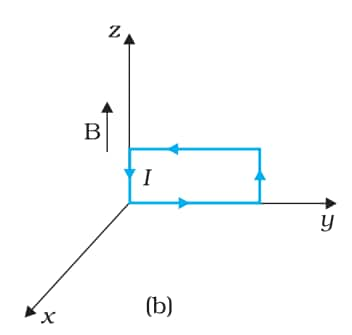
12.(b) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig? What is the force on each case? Which case corresponds to stable equilibrium?

Answer:

The magnetic field is

$\vec{B} = 3000 G \hat{k} = 0.3 T \hat{k}$

Current in the loop=12 A

Area of the loop = length $\times$ breadth

A=0.1 $\times$ 0.05

A=0.005 m²

$\vec{A} = 0.005 m^{2} \hat{i}$ (same as that in the last case)

$\begin{aligned} \vec{τ} = I \vec{A} \times \vec{B} \\ \vec{τ} = 12 \times 0.005 \hat{i} \times 0.3 \hat{k} \\ \vec{τ} = - 0.018 \hat{j} \end{aligned}$

The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-y direction. The force on the loop is zero.

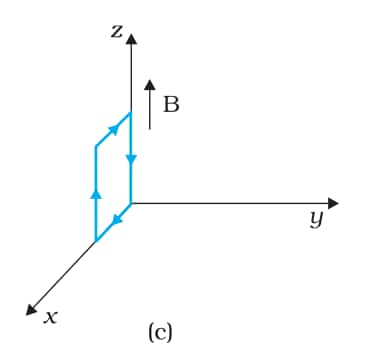
12 (c). A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig.? What is the force on each case? Which case corresponds to stable equilibrium?

Answer:

The magnetic field is

$\vec{B} = 3000 G \hat{k} = 0.3 T \hat{k}$

Current in the loop=12 A

Area of the loop = length $\times$ breadth

A=0.1 $\times$ 0.05

A=0.005 m²

$\vec{A} = - 0.005 m^{2} \hat{j}$

Torque is given by,

$\begin{aligned} \vec{τ} = I \vec{A} \times \vec{B} \\ \vec{τ} = 12 \times - 0.005 \hat{j} \times 0.3 \hat{k} \\ \vec{τ} = - 0.018 \hat{i} \end{aligned}$

The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-x-direction. The force on the loop is zero.

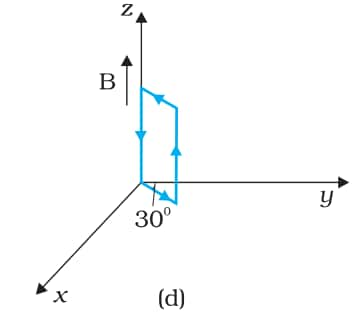
12 (d) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig.? What is the force on each case? Which case corresponds to stable equilibrium?

Answer:

The magnetic field is

$\vec{B} = 3000 G \hat{k} = 0.3 T \hat{k}$

Current in the loop=12 A

Area of the loop = length $\times$ breadth

A=0.1 $\times$ 0.05

A=0.005 m²

$\vec{A} = 0.005 m^{2} (- \frac{\hat{i}}{2} + \frac{\sqrt{3}}{2} \hat{j})$

Torque is given by,

$\begin{aligned} \vec{τ} = I \vec{A} \times \vec{B} \\ \vec{τ} = 12 \times 0.005 (- \frac{\hat{i}}{2} + \frac{\sqrt{3}}{2} \hat{j}) \times 0.3 \hat{k} \\ \vec{τ} = - 0.018 (\frac{\hat{i}}{2} + \frac{\sqrt{3}}{2} \hat{j}) \end{aligned}$

The torque on the loop has a magnitude of 0.018 Nm and at an angle of 240^o from the positive x-direction. The force on the loop is zero.

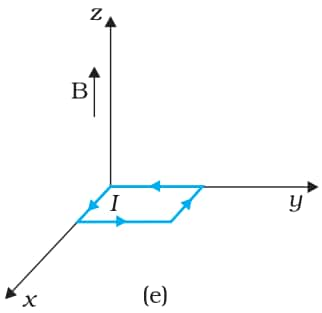
12. (e) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig.? What is the force on each case? Which case corresponds to stable equilibrium?

Answer:

The magnetic field is

$\vec{B} = 3000 G \hat{k} = 0.3 T \hat{k}$

Current in the loop=12 A

Area of the loop = length $\times$ breadth

A=0.1 $\times$ 0.05

A=0.005 m²

$\vec{A} = 0.005 m^{2} \hat{k}$

Since the area vector is along the direction of the magnetic field the torque on the loop is zero. The force on the loop is zero.

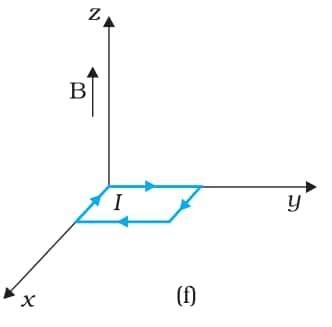
12 (f) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig.? What is the force on each case? Which case corresponds to stable equilibrium?

Answer:

The magnetic field is

$\vec{B} = 3000 G \hat{k} = 0.3 T \hat{k}$

Current in the loop=12 A

Area of the loop = length $\times$ breadth

A=0.1 $\times$ 0.05

A=0.005 m²

$\vec{A} = - 0.005 m^{2} \hat{k}$

Since the area vector is in the opposite direction of the magnetic field the torque on the loop is zero. The force on the loop is zero.

The force on the loop in all the above cases is zero as the magnetic field is uniform

13. (a) A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the total torque on the coil?

Answer:

As we know the torque on a current-carrying loop in a magnetic field is given by the following relation

$\vec{τ} = I \vec{A} \times \vec{B}$

It is clear that the torque, in this case, will be 0 as the area vector is along the magnetic field only.

13. (b) A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, total force on the coil.

Answer:

The total force on the coil will be zero as the magnetic field is uniform.

13 (c) A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area $10^{- 5} m^{2}$ , and the free electron density in copper is given to be about $10^{29} m^{- 3}$ .)

Answer:

The average force on each electron in the coil due to the magnetic field will be eV d B where V d is the drift velocity of the electrons.

The current is given by

$I = n e A v_{d}$

where n is the free electron density and A is the cross-sectional area.

$v_{d} = \frac{I}{n e A}$
$v_{d} = \frac{5}{10^{29} \times 1.6 \times 10^{- 19} \times 10^{- 5}}$

$v_{d} = 3.125 \times 10^{- 5} m s^{- 1}$

The average force on each electron is

$F = e v_{d} B$

$F = 1.6 \times 10^{- 19} \times 3.125 \times 10^{- 5} \times 00.1$

$F = 5 \times 10^{- 25} N$

14. A solenoid 60 cm long and of radius 4.0 cm has 3 layers of windings of 300 turns each. A 2.0 cm long wire of mass 2.5 g lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of 6.0 A in the wire. What value of current (with an appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? $g = 9.8 m s^{- 2}$

Answer:

The magnetic field inside the solenoid is given by

$B = μ_{0} n I$

n is number of turns per unit length

$n = \frac{3 \times 300}{0.6}$

n=1500 m^-1

Current in the wire I_w = 6 A

Mass of the wire m = 2.5 g

Length of the wire l = 2 cm

The windings of the solenoid would support the weight of the wire when the force due to the magnetic field inside the solenoid balances weight of the wire

$\begin{aligned} B I_{w} l = m g \\ B = \frac{m g}{I_{w} l} \\ μ_{0} n I = \frac{m g}{I_{w} l} \\ I = \frac{m g}{I_{w} l μ_{0} n} \\ I = \frac{2.5 \times 10^{- 3} \times 9.8}{6 \times 0.02 \times 4 π \times 10^{- 7} \times 1500} \\ I = 108.37 A \end{aligned}$

Therefore a current of 108.37 A in the solenoid would support the wire.

15. A galvanometer coil has a resistance of $12 Ω$ and the metre shows full scale deflection for a current of 3 mA. How will you convert the metre into a voltmeter of range 0 to 18 V?

Answer:

The galvanometer can be converted into a voltmeter by connecting an appropriate resistor of resistance R in series with it.

At the full-scale deflection current(I) of 3 mA the voltmeter must measure a Voltage of 18 V.

The resistance of the galvanometer coil G = $12 Ω$

$I$ $\times$ $(R + G) = 18 V$

$R = \frac{18}{3 \times 10^{- 3}} - 12$

$R = 6000 - 12 = 5988 Ω$

The galvanometer can be converted into a voltmeter by connecting a resistor of resistance $5988 Ω$ in series with it.

16. A galvanometer coil has a resistance of $15 Ω$ and the metre shows full scale deflection for a current of 4 mA. How will you convert the metre into an ammeter of range 0 to 6 A?

Answer:

The galvanometer can be converted into an ammeter by connecting an appropriate resistor of resistance R in series with it.

At the full-scale deflection current(I) of 4 mA, the ammeter must measure a current of 6 A.

The resistance of the galvanometer coil is G = $15 Ω$

Since the resistor and galvanometer coil are connected in parallel the potential difference is the same across them.

$\begin{aligned} I G = (6 - I) R \\ R = \frac{I G}{6 - I} \\ R = \frac{4 \times 10^{- 3} \times 15}{6 - 4 \times 10^{- 3}} \\ R \approx 0.01 Ω \end{aligned}$

The galvanometer can be converted into an ammeter by connecting a resistor of resistance $0.01 Ω$ in parallel with it.

Understanding class 12 NCERT solutions on moving charges and magnetism is similar to constructing a tall building's base. It is essential for passing difficult entrance examinations like JEE and NEET (like the support system that holds up the building) and for performing well on your regular school exams (like the bricks at the bottom).

Recommended eBooks

Related eBooks & Sample Papers

Class 12 CBSE Board Exam 2013 Chemistry Sample Paper

1716+ Downloads

CBSE Class 12 Sample Paper English Elective 2025-26 with Solution

77+ Downloads

Class 12 Physics NCERT Chapter 4: Higher Order Thinking Skills (HOTS) Questions

Question 1: A charged particle is thrown into space with a uniform magnetic field and uniform electric field.
Choose the correct possibility of the path of the charged particle.
1) The path of a charged particle may be a straight line, cycloidal or helical.
2) The path of the charged particle may be elliptical.
3) If electric field is removed path of the charge particle must be circular
4) None of the above

Answer:

In a pure uniform electric field, any charged particle will either move in a straight line or a parabolic path.
In a pure uniform magnetic field, any charged particle will either move on a circular path or a helical path.
In the presence of an electric field and magnetic field, the charged particle may move on a straight line if magnetic force balances the electric force

This situation comes in the case of a velocity selector.
If the electric field and magnetic field are parallel then the charge particle will follow a helical path.
If the electric field and magnetic field are perpendicular to each other then the charged particle may follow the cycloidal path.
Hence, the answer is the option (1).

Question 2: A particle of charge ' $q$ ' and mass ' $m$ ' is thrown from origin with velocity $\vec{v} = v \hat{i} + v \hat{j}$ in the magnetic field $\vec{B} = B \hat{i}$ . Find out the correct statement
1) The coordinates of the charge particle at $t = \frac{2 π m}{q B}$ are $x = \frac{2 π m}{q B}; y = 0; z = 0$
2) The coordinates of the charge particle at $t = \frac{π m}{q B}$ are $x = \frac{π m v}{q B}; y = 0; z = \frac{- 2 m v}{q B}$
3) The coordinates of the charge particle at $t = \frac{π m}{6 q B}$ are $x = \frac{π m v}{6 q B}; y = \frac{m v}{2 q B}; z = - \frac{\sqrt{3}}{2} \frac{m v}{q B}$
4) All are incorrect

Answer:

The particle will follow the helical path, which has a circular projection in the Y – Z plane and a straight-line motion along the x-axis.

In the Y-Z plane, it will perform circular motion with

$R = \frac{m v}{q B}$ and $T = \frac{2 π m}{q B}$

and centre of circle is at $(Z = - R, Y = 0)$

At general time its $Y$ and $Z$ coordinate will be

$Y = R \sin θ, Z = - R (1 - \cos θ) and$

Its X coordinate increases linearly with speed v.
(a) at $t = \frac{2 π m}{qB} \Rightarrow θ = 2 π \Rightarrow x = \frac{2 π mv}{qB}; y = 0; z = 0$
(b) at $t = \frac{π m}{qB} \Rightarrow θ = π \Rightarrow x = \frac{π mv}{qB}; y = 0; z = (\frac{- 2 m v}{q B})$
(c) at $t = \frac{π m}{6 qB} \Rightarrow θ = π / 6 \Rightarrow x = \frac{π mv}{6 qB}; y = \frac{mv}{2 qB}; z = \frac{- mv}{qB} (1 - \frac{\sqrt{3}}{2})$

Hence, the answer is the option(1) and option(2).

Question 3: Choose the correct statement about magnetic field.
1) Any charged particle in the magnetic field must experience a force due to it.
2) Any moving charge particle in the magnetic field must experience force due to it.
3) The work done by magnetic force on a moving charge particle is always zero.
4) The work done by magnetic force on a current carrying wire maybe non-zero.

Answer:

The magnetic field can apply force on a moving charge particle if it's velocity is not parallel to magnetic field.
Result can be easily viewed on basis of Lorentz force.
It says the force is obtained by cross product of velocity of charge particle and magnetic field.
Magnetic force never does any work, neither on charge nor on current carrying wire.
Hence, the answer is the option (3).

Question 4: Two proton beams are moving parallel to each other with same velocity v along their beam direction at some separation. Find out the correct option(s):
1) Ratio of electrostatic repulsive and magnetic attraction force is $\frac{c^{2}}{v^{2}}$
2) Ratio of electrostatic repulsive and magnetic attraction force is $\frac{v^{2}}{c^{2}}$
3) Electrostatic force per unit length of any beam is $\frac{2 {Kn}^{2} e^{2}}{r}$
Magnetic force per unit length of any beam is $\frac{μ_{0} n^{2} e^{2} v^{2}}{2 π r}$
4) Electrostatic force per unit length of any beam is $\frac{μ_{0} n^{2} e^{2} v^{2}}{2 π r}$
Magnetic force per unit length of any beam is $\frac{2 {Kn}^{2} e^{2}}{r}$

Answer:

Let there be n protons in unit length
So charge / length, $λ =$ ne
Effective current in proton beam $=$ nev

Now electrostatic force per unit length of any beam

$F_{e} = \frac{2 K λ_{1} λ_{2}}{r} = \frac{2 K (ne) (ne)}{r}$
Magnetic force per unit length of any beam

$\begin{aligned} F_{m} = \frac{μ_{0} i_{1} i_{2}}{2 π r} = \frac{μ_{0} (nev) (nev)}{2 π r} \\ So, \frac{F_{e}}{F_{m}} = \frac{1}{μ_{0} \in_{0} v^{2}} = \frac{c^{2}}{v^{2}} \end{aligned}$

Hence, the correct answer is the option(1) and (3).

Question 5: A proton, a deuterium nucleus, and an alpha particle are accelerated through the same potential difference. Now, these particles are sent in a uniform magnetic field perpendicularly. Choose the correct ratio(s):
1) Their radii of circles $= 1 : \sqrt{2} : \sqrt{2}$
2) Their angular momentum $= 1 : 2 : 4$
3) Their frequencies of periodic motion $= 2 : 1 : 1$
4) All the above are correct

Answer:

If charge ' $q$ ' is accelerated through potential difference $Δ V$ , its kinetic energy will be :

$K.E. = q Δ V \Rightarrow \frac{1}{2} {mv}^{2} = q Δ V$
In a magnetic field,

$r = \frac{m v}{q B}; L = \frac{m^{2} v^{2}}{q B}; f = \frac{q B}{2 π m}$
Proton, deuterium, and a particle have charge and mass as $(e, m) (e, 2 m) & (2 e, 4 m)$ respectively.
(a) So, their ratio of radii :

$r_{p} : r_{d} : r_{α} = \frac{\sqrt{2 m e Δ V}}{e B} : \frac{\sqrt{4 m e Δ V}}{e B} : \frac{\sqrt{16 m e Δ V}}{2 e B} \Rightarrow r_{p} : r_{d} : r_{α} = 1 :$
$\sqrt{2} : \sqrt{2}$

(b) Their ratio of angular momentum :

$L_{p} : L_{d} : L_{α} = \frac{2 m e Δ V}{e B} : \frac{4 m e Δ V}{e B} : \frac{16 m e Δ V}{2 e B} \Rightarrow L_{p} : L_{d} : L_{α} = 1 :$

$f_{p} : f_{d} : f_{α} = \frac{e B}{2 π m} : \frac{e B}{4 π m} : \frac{2 e B}{8 π m} \Rightarrow f_{p} : f_{d} : f_{α} = 2 : 1 : 1$
Hence, the answer is the option (4).

CBSE Class 12th Syllabus: Subjects & Chapters

Select your preferred subject to view the chapters

NCERT Class 12 Physics Moving charges and Mangetism: Topics

Chapter 4 Moving charges and magnetism NCERT Class 12 physics addresses the nature of magnetic fields generated by moving electric charges, the properties of such fields, how they interact with other moving charges, and with currents. It prepares the ground to study the magnetic effects of current, which play an essential role both in electromagnetism and in modern technology.

4.1 Introduction
4.2 Magnetic Force
4.2.1 Sources And Fields
4.2.2 Magnetic Field, Lorentz Force
4.2.3 Magnetic Force On A Current-Carrying Conductor
4.3 Motion In A Magnetic Field
4.4 Magnetic Field Due To A Current Element, Biot-Savart Law
4.5 Magnetic Field On The Axis Of A Circular Current Loop
4.6 Ampere’S Circuital Law
4.7 The Solenoid
4.8 Force Between Two Parallel Currents, The Ampere
4.9 Torque On Current Loop, Magnetic Dipole
4.9.1 Torque On A Rectangular Current Loop In A Uniform Magnetic Field
4.9.2 Circular Current Loop As A Magnetic Dipole
4.10 The Moving Coil Galvanometer

Class 12 Physics Chapter 4 Exercise solutions: Important Formulas

The important formulas from Class 12 Physics Chapter 4 – Moving Charges and Magnetism are essential for solving exercise questions accurately. These formulas help in understanding magnetic force, field calculations, and motion of charged particles in magnetic fields.

1. Magnetic Force on a Moving Charge (Lorentz Force):

$F = q (\vec{v} \times \vec{B})$
Where:
$F =$ Force on the charge
$q =$ Charge of the particle
$\vec{v} =$ Velocity of the particle
$\vec{B} =$ Magnetic field
The force is perpendicular to both the velocity and magnetic field.

2. Magnetic Force on a Current-Carrying Conductor:

$F = I L B \sin θ$
Where:
$I =$ Current
$L =$ Length of the conductor
$B =$ Magnetic field
$θ =$ Angle between the magnetic field and the conductor

3. Magnetic Field due to a Current-Carrying Conductor (Biot-Savart Law):

$d B = \frac{μ_{0}}{4 π} \frac{I d l \sin θ}{r^{2}}$
Where:
$d B =$ Small magnetic field element
$I =$ Current
$d l =$ Small length of the conductor
$r =$ Distance from the point to the wire
$θ =$ Angle between $d l$ and the line joining the point and element

4. Magnetic Field due to a Long Straight Current-Carrying Wire:

$B = \frac{μ_{0} I}{2 π r}$
Where:
$I =$ Current
$r =$ Distance from the wire
$B =$ Magnetic field at a distance $r$ from the wire

5. Ampere's Law:

$\oint \vec{B} \cdot d \vec{l} = μ_{0} I_{enc}$
Where:
$\oint \vec{B} \cdot d \vec{l} =$ Line integral of the magnetic field
$μ_{0} =$ Permeability of free space
$I_{enc} =$ Total enclosed current

6. Magnetic Field due to a Circular Loop:

$B = \frac{μ_{0} I}{2 R}$ at the center of the loop
Where:
$I =$ Current in the loop
$R =$ Radius of the loop

7. Force between Two Parallel Current-Carrying Conductors:

$F = \frac{μ_{0} I_{1} I_{2} L}{2 π r}$
Where:
$I_{1}, I_{2} =$ Currents in the two wires
$L =$ Length of the wire
$r =$ Distance between the wires

Approach to Solve Questions of Moving Charge and Magnetism Class 12

Moving Charges and Magnetism is basically about how moving electric charges can generate a magnetic field. It also explains the magnetic force and nature of a magnetic field. There are two important laws discussed in the chapter as well: the Ampere Law and the Biot-Savart Law. The laws describe the behaviour of moving charges in terms of current-carrying conductors as the cause of creating magnetic fields. An example is when you switch on an electric fan and the wires give the current that generates a magnetic field, consequently causing the motor of the fan to spin. Know what the approach should be to cover this chapter.

Learn about the Concept First

Revise simple concepts such as magnetic force on a moving charge, magnetic field resulting from a current element (Biot-Savart Law), and Ampere Circuital Law.
Obtain the directions of the vectors through the use of the right-hand rule.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Make Neat Diagram

When loop or wires are carrying current draw the correct diagrams indicating the current flow and magnetic field lines.

Apply Right-Hand Rules

The direction of magnetic field caused by current may by found by right-hand thumb rule.
Use the rule of Lorentz force (F = q(v x B)) on moving charge.

Determine the required Formula

Identify the concept underlying the question:

Moving charge and magnetic force
Biot-Savart Law
The forces acting on a current-carrying wire
Movement of charged particles in magnetic fields
Applications of Ampere law

What Extra Should Students Study Beyond the NCERT for JEE/NEET?

While NCERT provides a strong foundation, students preparing for JEE and NEET need to go beyond it for advanced concepts and practice. The comparison table below highlights the additional study requirements for each exam beyond the NCERT syllabus.

Concept Name	JEE	NCERT
Biot-savart Law	✅	✅
Magnetic Field Due To Current In Straight Wire	✅	✅
Magnetic Field Due To Circular Current Loop	✅	✅
Magnetic Field On The Axis Of Circular Current Loop	✅	✅
Ampere's Circuital Law And Its Applications	✅	✅
Solenoid	✅	✅
Toroid	✅	❌
Force On A Moving Charge In Magnetic Field	✅	✅
Motion Of A Charged Particle In Uniform Magnnetic Field	✅	✅
Lorentz Force	✅	✅
Cyclotron	✅	❌
Force On A Conductor Carrying Current In A Magnetic Field	✅	✅
Force Between Two Parallel Current Carrying Conductors	✅	✅
Torque On Current Loop And Magnetic Moment Derivation	✅	✅
Magnetic Moment Of Revolving Electron And Bohr Magneton	✅	❌
Moving Coil Galvanometer	✅	✅

Importance in Exams:

As the CBSE board exam is concerned, the solutions of NCERT Class 12 Physics chapter 4 Moving Charges and Magnetism is important. In CBSE board exams, 12 % of questions are asked from chapters 4 and 5. Same questions discussed in the chapter 4 Physics Class 12 NCERT solutions can be expected in the board exams.

NCERT Solutions for Class 12 Physics: Chapter-Wise

Here are the exercise-wise solutions of the NCERT Class 12 physics book:

NCERT solutions for Class 12 Physics Chapter 1 Electric Charges and Fields

NCERT solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance

NCERT solutions for Class 12 Physics Chapter 3 Current Electricity

NCERT solutions for Class 12 Physics Chapter 4 Moving charges and magnetism

NCERT solutions for Class 12 Physics Chapter 5 Magnetism and Matter

NCERT solutions for Class 12 Physics Chapter 6 Electromagnetic Induction

NCERT solutions for Class 12 Physics Chapter 7 Alternating Current

NCERT solutions for Class 12 Physics Chapter 8 Electromagnetic Waves

NCERT solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments

NCERT solutions for Class 12 Physics Chapter 10 Wave Optics

NCERT solutions for Class 12 Physics Chapter 11 Dual nature of radiation and matter

NCERT solutions for Class 12 Physics Chapter 12 Atoms

NCERT solutions for Class 12 Physics Chapter 13 Nuclei

NCERT Solutions for Class 12 Physics Chapter 14 Semiconductor Electronics Materials Devices And Simple Circuit

Also, check NCERT Books and NCERT Syllabus here:

NCERT solutions subject-wise

Also, check NCERT Exemplar Class 12 Solutions

Frequently Asked Questions (FAQs)

Q: What is the weightage of NCERT physics chapter 4 for CBSE board exam

The chapter Moving Charges and Magnetism have 8 to 10 percentage weightage. The questions asked from the chapter can be of a numerical, derivation or theory questions. CBSE board follows NCERT Syllabus. To practice problems refer to NCERT text book, NCERT syllabus and previous year board papers of Class 12 Physics.

Q: Can I skip the chapter moving charges for NEET preperation

No, you can not skip it. Since from NCERT Class 12 Physics chapter 4 you can expect 2 questions for NEET exam.

Q: Can I crack JEE Main questions from Moving Charges and Magnetism just by knowing the equations in the NCERT

No, you have to practise more questions for doing well in JEE main exams. The questions of Moving Charges and Magnetism need a good base of vectors and a thorough understanding of concepts

Articles

NCERT Exemplar Class 12 Chemistry Solutions chapter 16 Chemistry in Everyday life

5 days ago

NCERT Resources

NCERT Exemplar Class 12 Chemistry Solutions - Chapter Wise Problems with Solutions

5 days ago

NCERT Resources

NCERT Exemplar Class 12 Chemistry Solutions chapter 13 Amines

5 days ago

NCERT Resources

NCERT Exemplar Class 12 Chemistry Solutions Chapter 15 Polymers

5 days ago

NCERT Resources

Upcoming School Exams

National Means Cum-Merit Scholarship

Ongoing Dates

NMMS Application Date

25 Jul'25 - 30 Sep'25 (Online)

Assam High School Leaving Certificate Examination

Ongoing Dates

Assam HSLC Application Date

1 Sep'25 - 4 Oct'25 (Online)

Telangana Open School Society Intermediate Examination

Ongoing Dates

TOSS Intermediate Late Fee Application Date

8 Sep'25 - 20 Sep'25 (Online)

Admit Card

Result

Certifications By Top Providers

Introduction to Accounting-Part 1 Basics of Financial Statements

Via Indian Institute of Management Bangalore

Basic 3D Animation using Blender

Via Indian Institute of Technology Bombay

People Management with Impact

Via Indian Institute of Management Bangalore

Essentials of Program Strategy and Evaluation

Via Stanford University, Stanford

Preparing for the AP English Language and Composition Exam

Via Tennessee Board of Regents

Learn to Speak Korean 1

Via Yonsei University, Seoul

1074 courses

817 courses

394 courses

273 courses

Harvard University, Cambridge

97 courses

University of Michigan, Ann Arbor

83 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

Environmental Studies

History

Psychology

Artificial Intelligence

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Delaware, Newark

Newark, DE 19716

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Bristol Baptist College, Bristol

The Promenade, Clifton Down, Bristol BS8 3NJ

Cost of Living in South Korea for Indian Students 2025

11 min ⋆ May 21, 2025 11:05 AM IST

Cheapest Universities in London For International Students 2025

12 min ⋆ Sep 09, 2025 11:09 AM IST

Study MBBS in Kyrgyzstan 2025: Fees, Top Medical Colleges

15 min ⋆ Apr 07, 2025 05:04 AM IST

MBBS in Uzbekistan 2025: Fees, Top Medical Colleges & Admission Process

16 min ⋆ Sep 09, 2025 10:09 AM IST

Study in Dubai 2025-26: Cost, Admission Process, Eligibility, Visa, Scholarship

13 min ⋆ Sep 09, 2025 09:09 AM IST

GMAT 2025 Exam: Dates, Registration, Fees, Eligibility, Syllabus, Pattern, Result

28 min ⋆ Sep 09, 2025 09:09 AM IST

Questions related to CBSE Class 12th

On Question asked by student community

Have a question related to CBSE Class 12th ?

Can i improve my 12 result this year in PCM

Hello,

If you want to improve the Class 12 PCM results, you can appear in the improvement exam. This exam will help you to retake one or more subjects to achieve a better score. You should check the official website for details and the deadline of this exam.

I hope it will clear your query!!

Read Complete Answer

Rahul Mandal

8 Sep'25

how may marks should i get in my 12th board exams to get fee concesion in sastra university

Hello Aspirant,

SASTRA University commonly provides concessions and scholarships based on merit in class 12 board exams and JEE Main purposes with regard to board merit you need above 95% in PCM (or on aggregate) to get bigger concessions, usually if you scored 90% and above you may get partial concessions. I suppose the exact cut offs may change yearly on application rates too.

Read Complete Answer

gopi

4 Sep'25

Which course is best for computer science students after 12th standard

Hello,

After 12th, if you are interested in computer science, the best courses are:

B.Tech in Computer Science Engineering (CSE) – most popular choice.
BCA (Bachelor of Computer Applications) – good for software and IT jobs.
B.Sc. Computer Science / IT – good for higher studies and research.
B.Tech in Information Technology (IT) – focuses on IT and networking.

All these courses have good career scope. Choose based on your interest in coding, software, hardware, or IT field.

Hope it helps !

Read Complete Answer

Prachi Kumari

4 Sep'25

I am a CBSE class 12 private candidate will my maksheet of CBSE supplement exam will be delivered on main exam form address for supplementary exam form address ,my both addresses are different please tell

Hello Vanshika,

CBSE generally forwards the marksheet for the supplementary exam to the correspondence address as identified in the supplementary exam application form. It is not sent to the address indicated in the main exam form. Addresses that differ will use the supplementary exam address.

Read Complete Answer

gopi

3 Sep'25

12 arts previous years board paper 2025

To find Class 12 Arts board papers, go to the official website of your education board, then click on the Sample Papers, Previous Years Question Papers(PYQ) or Model Papers section, and select the Arts stream. You will find papers for the various academic year. You can then select the year of which you want to solve and do your practice. There are many other educational websites that post pyqs on their website you can also visit that.

Never miss an CBSE Class 12th update

Get timely CBSE Class 12th updates directly to your inbox. Stay informed!

Student Community: Where Questions Find Answers

Ask and get expert answers on exams, counselling, admissions, careers, and study options.

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Applications Open

JEE Test Series

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Class 12 Physics Chapter 4 - Moving Charges and Magnetism

Aakash Repeater Courses

NCERT Solutions for Class 12 Physics Chapter 4: Download PDF

NCERT Solutions for Class 12 Physics Chapter 4: Exercise Questions

NCERT Solutions for Class 12 Physics Chapter 4: Additional Questions

Related eBooks & Sample Papers

Class 12 Physics NCERT Chapter 4: Higher Order Thinking Skills (HOTS) Questions

NCERT Class 12 Physics Moving charges and Mangetism: Topics

Class 12 Physics Chapter 4 Exercise solutions: Important Formulas

1. Magnetic Force on a Moving Charge (Lorentz Force):

2. Magnetic Force on a Current-Carrying Conductor:

3. Magnetic Field due to a Current-Carrying Conductor (Biot-Savart Law):

4. Magnetic Field due to a Long Straight Current-Carrying Wire:

5. Ampere's Law:

6. Magnetic Field due to a Circular Loop:

7. Force between Two Parallel Current-Carrying Conductors:

Approach to Solve Questions of Moving Charge and Magnetism Class 12

What Extra Should Students Study Beyond the NCERT for JEE/NEET?

Importance in Exams:

NCERT Solutions for Class 12 Physics: Chapter-Wise

Also, check NCERT Books and NCERT Syllabus here:

NCERT solutions subject-wise

Also, check NCERT Exemplar Class 12 Solutions

Questions related to CBSE Class 12th

Popular CBSE Class 12th Questions

Study Resources, Applications and Opportunities

Aakash Repeater Courses

NEET Most scoring concepts

NEET Previous 10 Year Questions

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

JEE Main high scoring chapters and topics

CBSE Class 12th Notifications

Latest updates

Never miss an CBSE Class 12th update

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

NVS

JNVST

Schools By Medium

By Ownership

By City

By State

Download Careers360 App

All this at the convenience of your phone

Scan and download the app