NCERT Solutions for Class 12 Physics Chapter 2 - Electrostatic Potential and Capacitance

2.1 Two charges $5 \times 10^{-8}C$ and $-3 \times 10^{-8}C$ are located 16 cm apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.

Answer:

Given, two charge particles

$q_1= 5*10^{-8}C$

$q_2= -3*10^{-8}C$

The separation between two charged particle $d=16cm=0.16m$

Now, let's assume the point P between two charged particles where the electric potential is zero is x meter away from $q_1$ and $( 9-x)$ meter away from $q_2$

So,

The potential at point P :

$V_p=\frac{kq_1}{x}+\frac{kq_2}{0.16-x}=0$

$V_p=\frac{k5*10^{-8}}{x}+\frac{k(-3*10^{-8})}{0.16-x}=0$

$\frac{k5*10^{-8}}{x}=-\frac{k(-3*10^{-8})}{0.16-x}$

$5(0.16-x)=3x$

$x=0.1m=10cm$

Hence the point between two charged particles where the electric potential is zero lies 10cm away from $q_1$ and 6 cm away from $q_2$

Now, Let's assume a point Q which is outside the line segment joining two charges and having zero electric potential .let the point Q lie r meter away from $q_2$ and (0.16+r) meter away from $q_1$

So electric potential at point Q = 0

$\frac{kq_1}{0.16+r}+\frac{kq_2}{r}=0$

$\frac{k5*10^{-8}}{0.16+r}+\frac{k(-3*10^{-8})}{r}=0$

$5r=3(0.16+r)$

$r=0.24m=24cm$

Hence the second point where the electric potential is zero is 24cm away from $q_2$ and 40cm away from $q_1$

2.2 A regular hexagon of side 10 cm has a charge $5\mu C$ at each of its vertices. Calculate the potential at the centre of the hexagon.

Answer:

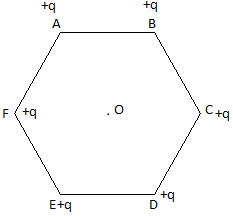
The electric potential at O due to one charge,

$V_1 = \frac{q}{4\pi\epsilon_0 r}$

q = 5 × 10 ^-6 C

r = distance between charge and O = 10 cm = 0.1 m

Using the superposition principle, each charge at corners contribute in the same direction to the total electric potential at point O.

$V = 6\times\frac{q}{4\pi\epsilon_0 r}$

$\implies V = 6\times\frac{9\times10^9 Nm^2C^{-2}\times5\times10^{-6}C}{0.1m}= 2.7 \times 10^6 V$

Therefore the required potential at the centre is $2.7 \times 10^6 V$

2.3 (a) Two charges $2\mu C$ and $-2\mu C$ are placed at points A and B 6 cm apart. Identify an equipotential surface of the system.

Answer:

Given, 2 charges with charges $2\mu C$ and $-2\mu C$ .

An equipotential plane is a plane where the electric potential is the same at every point on the plane. Here if we see the plane which is perpendicular to line AB and passes through the midpoint of the line segment joining A and B, we see that at every point the electric potential is zero because the distance of all the points from two charged particles is same. Since the magnitude of charges is the same they cancel out the electric potential by them.

Hence required plane is plane perpendicular to line AB and passing through the midpoint of AB which is 3cm away from both charges.

2.3 (b) Two charges $2\mu C$ and $-2\mu C$ are placed at points A and B 6 cm apart. What is the direction of the electric field at every point on this surface?

Answer:

The direction of the electric field in this surface is normal to the plane and in the direction of line joining A and B. Since both charges have the same magnitude and different sign, they cancel out the component of the electric field which is parallel to the surface.

2.4 (a) A spherical conductor of radius 12 cm has a charge of $1.6 \times 10^{-7}C$ distributed uniformly on its surface. What is the electric field inside the sphere?

Answer:

Since the charge is uniformly distributed and it always remains on the surface of the conductor, the electric field inside the sphere will be zero.

2.4 (b) A spherical conductor of radius 12 cm has a charge of $1.6 \times 10^{-7}C$ distributed uniformly on its surface. What is the electric field just outside the sphere?

Answer:

Given,

Charge on the conductor $q=1.6*10^{-7}C$

The radius of a spherical conductor $R=12cm=0.12m$

Now,

the electric field outside the spherical conductor is given by:

$E=\frac{kq}{r^2}=\frac{1}{4\pi \epsilon }\frac{q}{r^2}=\frac{9*10^9*1.6*10^{-7}}{0.12^2}=10^5NC^{-1}$

Hence electric field just outside is $10^5NC^{-1}$ .

2.4 (c) A spherical conductor of radius 12 cm has a charge of $1.6\times 10^{-7}C$ distributed uniformly on its surface. What is the electric field at a point 18 cm from the centre of the sphere?

Answer:

Given,

charge on the conductor $q=1.6*10^{-7}C$

The radius of the spherical conductor $R=12cm=0.12m$

Now,

the electric field at point 18cm away from the centre of the spherical conductor is given by:

$E=\frac{kq}{r^2}=\frac{1}{4\pi \epsilon }\frac{q}{r^2}=\frac{9*10^9*1.6*10^{-7}}{0.18^2}=4.4*10^4NC^{-1}$

Hence electric field at the point 18cm away from the centre of the sphere is $4.4*10^4NC^{-1}$

2.5 A parallel plate capacitor with air between the plates has a capacitance of 8 pF $\left ( 1pF = 10^{-12}F \right )$ . What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant 6?

Answer:

As we know,

$C=\frac{\epsilon_r\epsilon_0 A}{d}$

where A= area of the plate

$\epsilon_0$ = permittivity of the free space

d = distance between the plates.

Now, Given

The capacitance between plates initially

$C_{initial}=8pF=\frac{\epsilon A}{d}$

Now, capacitance when the distance is reduced half and filled with the substance of dielectric 6

$C_{final}=\frac{6\epsilon_0 A}{d/2}=12\frac{\epsilon _0A}{d}=12*8pF=96pF$

Hence new capacitance is 96pF.

2.6 (a) Three capacitors each of capacitance 9 pF are connected in series. What is the total capacitance of the combination?

Answer:

Given, 3 capacitor of 9pF connected in series,

the equivalent capacitance when connected in series is given by

$\frac{1}{C_{equivalent}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}$

$\frac{1}{C_{equivalent}}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}=\frac{1}{3}$

$C_{equivalent}=3pF$

Hence total capacitance of the combination is 3pF

2.6 (b) Three capacitors each of capacitance 9 pF are connected in series. What is the potential difference across each capacitor if the combination is connected to a 120 V supply?

Answer:

Given,

Supply Voltage V = 120 V

The potential difference across each capacitor will be one-third of the total voltage

$V_c=\frac{V}{3}=\frac{120}{3}=40V$

Hence potential difference across each capacitor is 40V.

2.7 (a) Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel. What is the total capacitance of the combination?

Answer:

Given, 3 capacitors with $C_1=2pF,C_2=3pFandC_3=4pF$ are connected in series,

the equivalent capacitance when connected in parallel is given by

$C_{equivalant}=C_1+C_2+C_3$

$C_{equivalant}=2+3+4=9pF$

Hence, the equivalent capacitance is 9pF.

2.7 (b) Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel. Determine the charge on each capacitor if the combination is connected to a 100 V supply.

Answer:

Given, 3 capacitors connected in parallel with

$C_1=2pF$

$C_2=3pF$

$C_3=4pF$

Supply voltage $V=100V$

Since they are connected in parallel, the voltage across each capacitor is 100V.

So, charge on 2pf capacitor :

$Q_1=C_1V=2*10^{-12}*100=2*10^{-10}C$

Charge on 3pF capacitor:

$Q_2=C_2V=3*10^{-12}*100=3*10^{-10}C$

Charge on 4pF capacitor:

$Q_3=C_3V=4*10^{-12}*100=4*10^{-10}C$

Hence charges on capacitors are 200pC,300pC and 400pC respectively

2.8 In a parallel plate capacitor with air between the plates, each plate has an area of $6 \times 10^{-3}m^{2}$ and the distance between the plates is 3 mm. Calculate the capacitance of the capacitor. If this capacitor is connected to a 100 V supply, what is the charge on each plate of the capacitor?

Answer:

Given,

Area of the capacitor plate $A$ = $6 \times 10^{-3}m^{2}$

Distance between the plates $d=3mm$

Now,

The capacitance of the parallel plate capacitor is

$C=\frac{\epsilon_0 A}{d}$

$\epsilon _0$ = permittivity of free space = $8.854*10^{-12}N^{-1}m^{-2}C^{_2}$

putting all know value we get,

$C=\frac{8.854*10^{-12}*6*10^{-3}}{3*10^{-3}}=17.71*10^{-12}F=17.71pF$

Hence capacitance of the capacitor is 17.71pF.

Now,

Charge on the plate of the capacitor :

$Q=CV=17.71*10^{-12}*100=1.771*10^{-9}C$

Hence charge on each plate of the capacitor is $1.771*10^{-9}C$ .

2.9 (a) Explain what would happen if in the capacitor given in exercise 2.8, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates,while the voltage supply remained connected.

Answer:

Given,

The dielectric constant of the inserted mica sheet = 6

The thickness of the sheet = 3mm

Supply voltage $V = 100V$

Initial capacitance = $C_{initial}=1.771 *10^{-11}F$

Final capacitance = $KC_{initial}$

Final capacitance $ =6*1.771 *10^{-11}F$

Final capacitance $=106*10^{-12}F$

Final charge on the capacitor = $Q_{final}=C_{final}V$
$=106*10^{-12}*100$
$=106*10^{-10}C$

Hence on inserting the sheet charge on each plate changes to $106*10^{-10}C$ .

2.9 (b) Explain what would happen if in the capacitor given, a 3 mm thick mica sheet (of dielectric constant = 6) were inserted between the plates, after the supply was disconnected.

Answer:

If a 3mm mica sheet is inserted between plates of the capacitor after disconnecting it from the power supply, the voltage across the capacitor be changed. Since the charge on the capacitor can not go anywhere, if we change the capacitance (which we are doing by inserting mica sheet here), the voltage across the capacitor has to be adjusted accordingly.

As obtained from question number 8 charge on each plate of the capacitor is $1.771*10^{-9}C$

$V_{final}=\frac{Q}{C_{final}}=\frac{1.771\times10^{-9}}{106\times 10^{-12}}=16.7V$

2.10 A 12pF capacitor is connected to a 50V battery. How much electrostatic energy is stored in the capacitor?

Answer:

As we know,

the electrostatic energy stored in the capacitor is

$E=\frac{1}{2}CV^2$

Here,

$C= 12pF$

$V=50V$

So,

$E=\frac{1}{2}CV^2=\frac{1}{2}12*10^{-12}*50^2=1.5*10^{-8}J$

Hence energy stored in the capacitor is $1.5*10^{-8}J$

2.11 A 600pF capacitor is charged by a 200V supply. It is then disconnected from the supply and is connected to another uncharged 600 pF capacitor. How much electrostatic energy is lost in the process?

Answer:

Given

$C=600pF$

$V=200V$

Energy stored :

$E=\frac{1}{2}CV^2=\frac{1}{2}*600*10^{-12}*200*200=1.2*10^{-5}J$

Now, when it is disconnected and connected from another capacitor of capacitance 600pF

New capacitance

$C'=\frac{600*600}{600+600}=300pF$

New electrostatic energy

$E'=\frac{1}{2}C'V^2=\frac{1}{2}*300*10^{-12}*200^2=0.6*10^{-5}J$

Hence loss in energy

$E-E'=1.2*10^{-5}-0.6*10^{-5}J=0.6*10^{-5}J$

Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance: Additional Questions

1. A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of $-2\times 10^{-9}C$ from a point P (0, 0, 3 cm) to a point Q (0, 4 cm, 0), via a point R (0, 6 cm, 9 cm).

Answer:

Given,

The initial distance between two charges

$d_{initial}=3cm$

The final distance between two charges

$d_{final}=4cm$

Hence total work is done

$W=q_2\left ( \frac{kq_1}{d_{final}}-\frac{kq_1}{d_{initial}}\right )=\frac{kq_1q_2}{4\pi\epsilon _0}\left ( \frac{1}{d_{final}}-\frac{1}{d_{initial}} \right )$

$W=9*10^9*8*10^{-3}*(-2*10^{-9})\left ( \frac{1}{0.04}-\frac{1}{0.03} \right )=1.27J$

The path of the charge does not matter, only initial and final position matters.

2. A cube of side b has a charge q at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.

Answer:

As we know,

the distance between vertices and the centre of the cube

$d=\frac{\sqrt{3}b}{2}$

Where b is the side of the cube.

So potential at the centre of the cube:

$P=8*\frac{kq}{d}=8*\frac{kq}{b\sqrt{3}/2}=\frac{16kq}{b\sqrt{3}}$

Hence electric potential at the centre will be

$\frac{16kq}{b\sqrt{3}}=\frac{16q}{4\pi \epsilon_0 b\sqrt{3}}=\frac{4q}{\pi \epsilon_0 b\sqrt{3}}$

The electric field will be zero at the centre due to symmetry i.e. every charge lying in the opposite vertices will cancel each other's field.

3. (a) Two tiny spheres carrying charges $1.5 \mu C$ and $2.5 \mu C$ are located 30 cm apart. Find the potential and electric field at the mid-point of the line joining the two charges

Answer:

As we know

outside the sphere, we can assume it like a point charge. so,

the electric potential at midpoint of the two-sphere

$V=\frac{kq_1}{d/2}+\frac{kq_2}{d/2}$

where q1 and q2 are charges and d is the distance between them

So,

$V=\frac{k1.5*10^{-6}}{0.15}+\frac{k2.5*10^{-6}}{0.15}=2.4*10^5V$

The electric field

$E=\frac{k1.5*10^{-6}}{0.15^2}-\frac{k2.5*10^{-6}}{0.15^2}=4*10^5V/m$

3. (b) Two tiny spheres carrying charges $1.5 \mu C$ and $2.5 \mu C$ are located 30 cm apart. Find the potential and electric field at a point 10 cm from this midpoint in a plane normal to the line and passing through the mid-point.

Answer:

The distance of the point from both the charges :

$d=\sqrt{0.1^2+0.15^2}=0.18m$

Hence,

Electric potential:

$V=\frac{kq_1}{d}+\frac{kq_2}{d}=\frac{k}{0.18}(1.5+2.5)*10^{-6}=2*10^5V$

Electric field due to q1

$E_1=\frac{kq_1}{d^2}=\frac{k1.5\mu C}{0.18^2m^2}=0.416*10^6V/m$

Electric field due to q2

$E_2=\frac{kq_2}{d^2}=\frac{k2.5\mu C}{0.18^2m^2}=0.69*10^6V/m$

Now,

Resultant Electric field :

$E=\sqrt{E_1^2+E_2^2+2E_1E_2cos\theta}$

Where $\theta$ is the angle between both electric field directions

Here,

$cos\frac{\theta}{2}=\frac{0.10}{0.18}=\frac{5}{9}$

$\frac{\theta}{2}=56.25$

${\theta}=2*56.25=112.5$

Hence

$E=\sqrt{(0.416*10^6)^2+(0.69*10^6)^2+2(0.416*10^6)(0.69*10^6)cos112.5}$

$E=6.6*10^5V/m$

4. (a) A spherical conducting shell of inner radius r 1 and outer radius r 2 has a charge Q.A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?

Answer:

The charge placed on the centre is q, so -q will be the charge induced in the inner shell and + q will be induced in the outer shell

So,

charge density on the inner shell

$\sigma_{inner}=\frac{-q}{4\pi r_1^2}$

charge Density on the outer shell

$\sigma_{outer}=\frac{Q+q}{4\pi r_2^2}$

4. (b) A spherical conducting shell of inner radius r 1 and outer radius r 2 has a charge Q. Is the electric field inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape? Explain.

Answer:

Yes, the electric field inside the cavity is zero even when the shape is irregular and not the sphere. Suppose a Gaussian surface inside the cavity, now since there is no charge inside it, the electric flux through it will be zero according to the guess law. Also, all of the charges will reside on the surface of the conductor so, net charge inside is zero. hence electric field inside cavity is zero.

5. (a) Show that the normal component of the electrostatic field has a discontinuity from one side of a charged surface to another given by $(E_{1}-E_{2}).\widehat{n}= \frac{\sigma }{\epsilon _{0}}$

where $\hat{n}$ is a unit vector normal to the surface at a point and σ is the surface charge density at that point. Hence, show that just outside a conductor, the electric field is $\sigma \frac{\widehat{n}}{\epsilon _{0}}$ [Hint: Use Gauss’s law]

Answer:

The electric field on one side of the surface with charge density $\sigma$

$E_1=-\frac{\sigma}{2\epsilon _0}\widehat{n}$

The electric field on another side of the surface with charge density $\sigma$

$E_2=-\frac{\sigma}{2\epsilon _0}\widehat{n}$

Now, resultant of both surfaces:

As E_{1} and E_{2} are opposite in direction. we have

$E_1-E_2=\frac{\sigma}{2\epsilon _0}-\left ( -\frac{\sigma}{2\epsilon _0} \right )\widehat{n}=\frac{\sigma}{\epsilon _0}$

There has to be a discontinuity at the sheet of the charge since both electric fields are in the opposite direction.

Now,

Since the electric field is zero inside the conductor,

the electric field just outside the conductor is

$E=\frac{\sigma}{\epsilon _0}\widehat{n}$

5. (b) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another. [Hint: Use the fact that work done by electrostatic field on a closed loop is zero.]

Answer:

Let's assume a rectangular loop of length l and small width b.

Now,

Line integral along the loop :

$\oint E.dl=E_1l-E_2l=0$

This implies

$E_1cos\theta_1l-E_2cos\theta_2l=0$

From here,

$E_1cos\theta_1=E_2cos\theta_2$

Since $E_1cos\theta_1$ and $E_2cos\theta_2$ are the tangential component of the electric field, the tangential component of the electric field is continuous across the surface

6. A long charged cylinder of linear charged density $\lambda$ is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders?

Answer:

The charge density of the cylinder with length l and radius r = $\lambda$

The radius of another hollow cylinder with the same length = R

Now, let our gaussian surface be a cylinder with the same length and different radius r

the electric flux through Gaussian surface

$\oint E.ds=\frac{q}{\epsilon _0}$

$E.2\pi rl=\frac{\lambda l}{\epsilon _0}$

$E=\frac{\lambda }{2\pi \epsilon _0r}$

Hence electric field ar a distance r from the axis of the cylinder is

$E=\frac{\lambda }{2\pi \epsilon _0r}$

7. (a) In a hydrogen atom, the electron and proton are bound at a distance of about $0.53 \dot{A}$ Estimate the potential energy of the system in eV, taking the zero of the potential energy at an infinite separation of the electron from proton

Answer:

As we know,

the distance between electron-proton of the hydrogen atom

$d=0.53*10^{-10}m$

The potential energy of the system = potential energy at infinity - potential energy at distance d

$PE=0-\frac{ke*e}{d}=-\frac{9*10^9(1.6*10^{-19})^2}{0.53*10^{10}}=-43.7*10^{-19}J$

As we know,

$1ev=1.6*10^{-19}J$

$PE=\frac{-43.7*10^{-19}}{1.6*10^{-19}}=-27.2eV$

Hence potential energy of the system is -27.2eV.

7. (b) In a hydrogen atom, the electron and proton are bound at a distance of about $0.53 \dot{A}$ What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)?

Answer:

The potential energy of the system is -27.2eV. (from the previous question)

Kinetic energy is half of the potential energy in magnitude. so kinetic energy = 27/2 = 13.6eV

so,

total energy = 13.6 - 27.2 = -13.6eV

Hence the minimum work required to free the electron is 13.6eV

7. (c) In a hydrogen atom, the electron and proton are bound at a distance of about 0.53 $\dot{A}$. What are the answers to (a) and (b) above if the zero of potential energy is taken at 1.06 $\dot{A}$ separation?

Answer:

When potential energy is zero at $d'$ 1.06 $\dot{A}$ away,

The potential energy of the system =potential energy at $d'$ -potential energy at d

$PE=\frac{ke*p}{d_1}-27.2= \frac{9*10^{9}*(1.6*10^{-19})^2}{1.06*10^{-10}}=-13.6eV$

Hence potential energy, in this case, would be -13.6eV

8. If one of the two electrons of a H 2 molecule is removed, we get a hydrogen molecular ion $H^{+}_{2}$ . In the ground state of an $H^{+}_{2}$ , the two protons are separated by roughly 1.5 $\dot{A}$ , and the electron is roughly 1 $\dot{A}$ from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.

Answer:

Given,

Distance between proton 1 and 2

$d_{p_1-p_2}=1.5*10^{-10}m$

Distance between proton 1 and electron

$d_{p_1-e}=1*10^{-10}m$

Distance between proton 2 and electron

$d_{p_2-e}=1*10^{-10}m$

Now,

The potential energy of the system :

$V=\frac{kp_1e}{d_{p_1-e}}+\frac{kp_2e}{d_{p_2-e}}+\frac{kp_1p_2}{d_{p_1-p_2}}$

Substituting the values, we get

$V=\frac{9*10^{9}*10^{-19}*10^{-19}}{10^{-10}}\left [ -(16)^2+\frac{(1.6)^2}{1.5} -(1.6)^2\right ]=-19.2eV$

9. Two charged conducting spheres of radii a and b are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions.

Answer:

Since both spheres are connected through the wire, their potential will be the same

Let electric field at A and B be $E_A and E_B$ .

Now,

$\frac{E_A}{E_B}=\frac{Q_A}{Q_B}*\frac{b^2}{a^2}$

also

$\frac{Q_A}{Q_B}=\frac{C_aV}{C_BV}$

Also

$\frac{C_A}{C_B}=\frac{a}{b}$

Therefore,

$\frac{E_A}{E_B}=\frac{ab^2}{ba^2}=\frac{b}{a}$

Therefore the ratio of the electric field is b/a.

10. (a) Two charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively. What is the electrostatic potential at the points (0, 0, z) and (x, y, 0) ?

Answer:

1)electric potential at point (0,0,z)

distance from $q_1$

$d_1=\sqrt{0^2+0^2+(0-a-z)^2}=a+z$

distance from $q_2$

$d_2=\sqrt{0^2+0^2+(a-z)^2}=a-z$

Now,

Electric potential :

$V=\frac{kq_1}{a+z}+\frac{kq_2}{a-z}=\frac{2kqa}{z^2-a^2}$

2) Since the point,(x,y,0) lies in the normal to the axis of the dipole, the electric potential at this point is zero.

10. (b) Two charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively. Obtain the dependence of potential on the distance r of a point from the origin when $\frac{r}{a}>>1$

Answer:

Here, since distance r is much greater than half the distance between charges, the potential V at a distance r is inversely proportional to the square of the distance

$V\propto \frac{1}{r^2}$

10. (c) Two charges –q and +q are located at points (0, 0, –a) and (0, 0, a), respectively How much work is done in moving a small test charge from the point (5,0,0) to (–7,0,0) along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?

Answer:

Since point (5,0,0) is equidistance from both charges, they both will cancel out each other potential and hence potential at this point is zero.

Similarly, point (–7,0,0) is also equidistance from both charges. and hence potential at this point is zero.

Since potential at both the point is zero, the work done in moving charge from one point to other is zero. Work done is independent of the path.

11. Figure shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on r for $\frac{r}{a}>>1$ , and contrast your results with that due to an electric dipole, and an electric monopole (i.e., a single charge).

Answer:

Here, As we can see

The electrostatic potential caused by the system of three charges at point P is given by

$V = \frac{1}{4\pi \varepsilon _0}\left [ \frac{q}{r+a}-\frac{2q}{r}+\frac{q}{r-a} \right ]$

$V = \frac{1}{4\pi \varepsilon _0}\left [ \frac{r(r-a)-2(r+a)(r-a)+r(r+a)}{r(r+a)(r-a)}\right ]=\frac{q}{4\pi \epsilon _0}\left [ \frac{2a^2}{r(r^2-a^2)} \right ]$

$V =\frac{q}{4\pi \epsilon _0}\left [ \frac{2a^2}{r^3(1-\frac{a^2}{r^2})} \right ]$

Since

$\frac{r}{a}>>1$

$V=\frac{2qa^2}{4\pi \epsilon _0r^3}$

From here we conclude that

$V\propto \frac{1}{r^3}$

Whereas we know that for a dipole,

$V\propto \frac{1}{r^2}$

And for a monopole,

$V\propto \frac{1}{r}$

12. An electrical technician requires a capacitance of $2\mu F$ in a circuit across a potential difference of 1 kV. A large number of $1\mu F$ capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors

Answer:

Let's assume n capacitor connected in series and m number of such rows,

Now,

As given

The total voltage of the circuit = 1000V

and the total voltage a capacitor can withstand = 400

From here the total number of the capacitor in series

$n=\frac{1000}{400}=2.5$

Since the number of capacitors can never be a fraction, we take n = 3.

Now,

Total capacitance required = $2\mu F$

Number of rows we need

$m=2*n=2*3=6$

Hence capacitors should be connected in 6 parallel rows where each row contains 3 capacitors in series.

13. What is the area of the plates of a 2 F parallel plate capacitor, given that the separation between the plates is 0.5 cm? [You will realise from your answer why ordinary capacitors are in the range of $\mu F$ or less. However, electrolytic capacitors do have a much larger capacitance (0.1 F) because of very minute separation between the conductors.]

Answer:

Given,

The capacitance of the parallel plate capacitor $C=2F$

Separation between plated $d=0.5cm$

Now, As we know

$C=\frac{\epsilon _0A}{d}$

$A=\frac{Cd}{\epsilon _0}=\frac{2*5*10^{-3}}{8.85*10^{-12}}=1.13*10^9m^2$

$A=1.13*10^3km^2=1130km^2$

Hence, to get capacitance in farads, the area of the plate should be of the order of kilometre which is not good practice, and so that is why ordinary capacitors are of range $\mu F$

14. Obtain the equivalent capacitance of the network in Figure. For a 300 V supply, determine the charge and voltage across each capacitor.

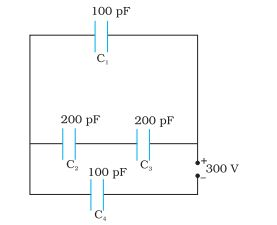
Answer:

Given.

$C_1=100pF$

$C_2=200pF$

$C_3=200pF$

$C_4=100pF$

Now,

Lets first calculate the equivalent capacitance of $C_2\: and \:C_3$

$C_{23}=\frac{C_2C_3}{C_2+C_3}=\frac{200*200}{200+200}=100pF$

Now let's calculate the equivalent of $C_1\:and\:C_{23}$

$C_{1-23}=C_1+C_{23}=100+100=200pF$

Now let's calculate the equivalent of $C_{1-23} \: and \:C_4$

$C_{equivalent}=\frac{C_{1-23}*C_4}{C_{1-23}+C_4}=\frac{100*200}{100+200}=\frac{200}{3}pF$

Now,

The total charge on $C_4$ capacitors:

$Q_4=C_{equivalent}V=\frac{200}{3}*10^{-12}*300=2*10^{-8}C$

So,

$V_4=\frac{Q_4}{C_4}=\frac{2*10^{-8}}{100*10^{-12}}=200V$

The voltage across $C_1$ is given by

$V_{1}=V-V_{4}=300-200=100V$

The charge on $C_1$ is given by

$Q_1=C_1V_1=100*10^{-12}*100=10^{-8}C$

The potential difference across $C_2\:and\:C_3$ is

$V_2=V_3=50V$

Hence Charge on $C_2$

$Q_2=C_2V_2=200*10^{-12}*50=10^{-8}C$

And Charge on $C_3$ :

$Q_3=C_3V_3=200*10^{-12}*50=10^{-8}C$

15. (a) The plates of a parallel plate capacitor have an area of 90 cm 2 each and are separated by 2.5 mm. The capacitor is charged by connecting it to a 400 V supply. How much electrostatic energy is stored by the capacitor?

Answer:

Here

The capacitance of the parallel plate capacitor :

$C=\frac{\epsilon_0 A}{d}$

The electrostatic energy stored in the capacitor is given by :

$E=\frac{1}{2}CV^2=\frac{1}{2}\frac{\varepsilon _0A}{d}V^2 =\frac{1.885*10^{-12}90*10^{-4}*400^2}{2*2.5*10^{-3}}=2.55*10^{-6}J$

Hence, the electrostatic energy stored by the capacitor is $2.55*10^{-6}J$.

15. (b) The plates of a parallel plate capacitor have an area of 90 cm2 each and are separated by 2.5 mm. The capacitor is charged by connecting it to a 400 V supply. View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume u. Hence arrive at a relation between u and the magnitude of electric field E between the plates.

Answer:

The volume of the capacitor is:

$V=A*d=90*10^{-4}25*10^{-3}=2.25*10^{-4}m^3$

Now,

Energy stored in the capacitor per unit volume :

$u =\frac{E}{V}=\frac{2.55*10^{-6}}{2.55*10^{-4}}=0.113per \:m^3$

Now, the relation between u and E.

$u =\frac{E}{V}=\frac{\frac{1}{2}CV^2}{Ad}=\frac{\frac{1}{2}(\frac{\epsilon _0A}{d})V^2}{Ad}=\frac{1}{2}\epsilon _0E^2$

16. A 4 $\mu F$ capacitor is charged by a 200 V supply. It is then disconnected from the supply and is connected to another uncharged 2 $\mu F$ capacitors. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation?

Answer:

Here,

The charge on the capacitance Initially

$Q=CV=4*10^{-6}*200=8*10^{-4}C$

Total electrostatic energy initially

$E_{initial}=\frac{1}{2}CV^2=\frac{1}{2}4*10^{-6}*(200)^2=8*10^{-2}J$

Now, when it is disconnected and connected to another capacitor

Total new capacitance = $C_{new}=4+2=6\mu F$

Now, by conserving the charge on the capacitor:

$V_{new}C_{new}=C_{initial}V_{initial}$

$V_{new}6\mu F=4\mu F *200$

$V_{new}=\frac{400}{3}V$

Now,

New electrostatic energy :

$E_{new}=\frac{1}{2}C_{new}V_{new}^2=\frac{1}{2}*6*10^{-6}*\left ( \frac{400}{3} \right )^2=5.33*10^{-2}J$

Therefore,

Lost in electrostatic energy

$E=E_{initial}-E_{new}=0.08-0.0533=0.0267J$

17. Show that the force on each plate of a parallel plate capacitor has a magnitude equal to $\left (\frac{1}{2} \right )$ QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor $\left (\frac{1}{2} \right )$

Answer:

Let

The surface charge density of the capacitor = $\sigma$

Area of the plate = $A$

Now,

As we know,

$Q=\sigma A\:and \: E=\frac{\sigma}{\epsilon _0}$

When the separation is increased by $\Delta x$ ,

work done by external force= $F\Delta x$

Now,

Increase in potential energy :

$\Delta u=u*A\Delta x$

By work-energy theorem,

$F\Delta x=u*A\Delta x$

$F=u*A=\frac{1}{2}\epsilon _0E^2A$

putting the value of $\epsilon _0$

$F=\frac{1}{2}\frac{\sigma}{E}E^2A=\frac{1}{2}\sigma AE=\frac{1}{2}QE$

origin of 1/2 lies in the fact that field is zero inside the conductor and field just outside is E, hence it is the average value of E/2 that contributes to the force.

18. A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports figure. Show that the capacitance of a spherical capacitor is given by $C = \frac{4\pi \epsilon_{0}r_{1}r_{2}}{r_{1}-r_{2}}$ where r_{1 } and r_{2} are the radii of outer and inner spheres, respectively.

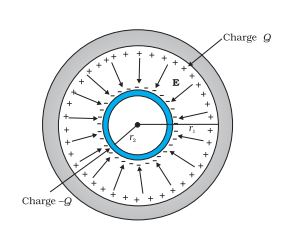
Answer:

Given

the radius of the outer shell = $r_1$

the radius of the inner shell = $r_2$

charge on Inner surface of outer shell = $Q$

Induced charge on the outer surface of inner shell = $-Q$

Now,

The potential difference between the two shells

$V=\frac{Q}{4\pi \epsilon _0r_2}-\frac{Q}{4\pi \epsilon _0r_1}$

Now Capacitance is given by

$C=\frac{Charge(Q)}{Potential\:difference(V)}$

$C=\frac{Q}{\frac{Q(r_1-r_2)}{4\pi \epsilon _0r_1r_2}}=\frac{4\pi \epsilon _0r_1r_2}{r_1-r_2}$

Hence proved.

19. (a) A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 $\mu C$ . The space between the concentric spheres is filled with a liquid of dielectric constant 32. Determine the capacitance of the capacitor.

Answer:

The capacitance of the capacitor is given by:

$C=\frac{4\pi \epsilon _0\epsilon _rr_1r_2}{r_1-r_2}$

Here,

$C=\frac{32*0.12*0.13}{9*10^9*(0.13-0.12)}=5.5*10^{-9}F$

Hence Capacitance of the capacitor is $5.5*10^{-9}F$ .

19. (b) A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 $\mu C$ . The space between the concentric spheres is filled with a liquid of dielectric constant 32. What is the potential of the inner sphere?

Answer:

Potential of the inner sphere is given by

$V=\frac{q}{C}=\frac{2.5*10^{-6}}{5.5*10^{-9}}=4.5*10^2$

Hence the potential of the inner sphere is $4.5*10^2 V$ .

19. (c) A spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5 $\mu$ C. The space between the concentric spheres is filled with a liquid of dielectric constant 32. Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm. Explain why the latter is much smaller.

Answer:

The radius of the isolated sphere $r = 4.5*10^2$

Now, Capacitance of sphere:

$C_{new}=4\pi\epsilon _0r=4\pi 8.85*10^{-12}*12*10^{-12}=1.33*10^{-11}F$

On comparing it with the concentric sphere, it is evident that it has lesser capacitance.this is due to the fact that the concentric sphere is connected to the earth.

Hence the potential difference is less and capacitance is more than the isolated sphere.

20. (a) Two large conducting spheres carrying charges Q_{1} and Q_{2 } are brought close to each other. Is the magnitude of electrostatic force between them exactly given by $\frac{Q_{1}Q_{2}}{4\pi \epsilon_{0}r^{2}}$ , where r is the distance between their centres?

Answer:

The charge on the sphere is not exactly a point charge, we assume it when the distance between two bodies is large. when the two charged sphere is brought closer, the charge distribution on them will no longer remain uniform. Hence it is not true that electrostatic force between them exactly given by $\frac{Q_{1}Q_{2}}{4\pi \epsilon_{0}r^{2}}$ .

20. (b) If Coulomb’s law involved $\frac{1}{r^{3}}$ dependence (instead of $\frac{1}{r^{2}}$ ), would Gauss’s law be still true?

Answer:

Since the solid angle is proportional to $\frac{1}{r^2}$ and not proportional to $\frac{1}{r^3}$ ,

The guass law which is equivalent of coulombs law will not hold true.

20. (c) A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?

Answer:

When a small test charge is released at rest at a point in an electrostatic field configuration it travels along the field line passing through that point only if the field lines are straight because electric field lines give the direction of acceleration, not the velocity

20. (d) What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?

Answer:

The initial and final position will be the same for any orbit whether it is circular or elliptical. Hence work done will always be zero.

20. (e) We know that electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?

Answer:

Since the electric potential is not a vector quantity unlike the electric field, it can never be discontinuous.

20. (f) What meaning would you give to the capacitance of a single conductor?

Answer:

There is no meaning in the capacitor with a single plate factually. but we give it meaning by assuming the second plate at infinity. Hence capacitance of a single conductor is the amount of change required to raise the potential of the conductor by one unit amount.

20. (g) Guess a possible reason why water has a much greater dielectric constant (= 80) than say, mica (= 6).

Answer:

Water has a much greater dielectric constant than mica because it possesses a permanent dipole moment and has an unsymmetrical shape.

21. A cylindrical capacitor has two co-axial cylinders of length 15 cm and radii 1.5 cm and 1.4 cm. The outer cylinder is earthed and the inner cylinder is given a charge of 3.5 $\mu$ C. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i.e., bending of field lines at the ends).

Answer:

Given

Length of cylinder $l=15cm$

inner radius $a=1.4cm$

outer radius $b=1.5cm$

Charge on the inner cylinder $q=3.5\mu C$

Now as we know,

The capacitance of this system is given by

$C=\frac{2\pi \epsilon _0l}{2.303log_{10}(b/a)}$

$C=\frac{2\pi *8.854*10^{-12}*15*10^{-2}}{2.303log_{10}(1.5*10^{-2}/1.4*10^{-2})}=1.21*10^{-10}F$

Now

Since the outer cylinder is earthed the potential at the inner cylinder is equal to the potential difference between two cylinders.

So

Potential of inner cylinder:

$V=\frac{q}{C}=\frac{3.5*10^{-6}}{1.21*10^{-10}}=2.89*10^4V$

22. A parallel plate capacitor is to be designed with a voltage rating 1 kV, using a material of dielectric constant 3 and dielectric strength about $10^{-7}Vm^{-1}$ . (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i.e., without starting to conduct electricity through partial ionisation.) For safety, we should like the field never to exceed, say 10% of the dielectric strength. What minimum area of the plates is required to have a capacitance of 50 pF?

Answer:

Given

Voltage rating in designing capacitor $V=1kV=1000V$

The dielectric constant of the material $K=\epsilon _r=3$

Dielectric strength of material = $10^7V/m$

Safety Condition:

$E=\frac{10}{100}*10^7=10^6V/m$

The capacitance of the plate $C=50pF$

Now, As we know,

$E=\frac{V}{d}$

$d=\frac{V}{E}=\frac{10^3}{10^6}=10^{-3}m$

Now,

$C=\frac{\varepsilon _0\varepsilon_rA }{d}$

$A=\frac{Cd}{\epsilon_0 \epsilon_r }=\frac{50*10^{-12}*10^{-3}}{8.85*10^{-12}*3}=1.98*10^{-3}m^2$

Hence the minimum required area is $1.98*10^{-3}m^2$

23. (a) Describe schematically the equipotential surfaces corresponding to a constant electric field in the z-direction

Answer:

When the electric field is in the z-direction is constant, the potential in a direction perpendicular to z-axis remains constant. In other words, every plane parallel to the x-y plane is an equipotential plane.

23. (b) Describe schematically the equipotential surfaces corresponding to a field that uniformly increases in magnitude but remains in a constant (say, z) direction

Answer:

The potential in a direction perpendicular to the direction of the field is always gonna be same irrespective of the magnitude of the electric field. Hence equipotential surface will be the plane, normal of which is the direction of the field.

23. (c) Describe schematically the equipotential surfaces corresponding to a single positive charge at the origin.

Answer:

For a single positive charge, the equipotential surface will be the sphere with centre at position of the charge which is origin in this case.

23. (d) Describe schematically the equipotential surfaces corresponding to a uniform grid consisting of long equally spaced parallel charged wires in a plane.

Answer:

The equipotential surface near the grid is periodically varying.and after long distance it becomes parallel to the grid.

24. A small sphere of radius r_{1} and charge q_{1} is enclosed by a spherical shell of radius r_{2} and charge q_{2}. Show that if q_{1} is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q_{2} on the shell is.

Answer:

The potential difference between the inner sphere and shell;

$V=\frac{1}{4\pi \epsilon _0}\frac{q_1}{r_1}$

So, the potential difference is independent of $q_2$ . And hence whenever q_{1} is positive, the charge will flow from sphere to the shell

25. (a) The top of the atmosphere is at about 400 kV with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about 100 $Vm^{-1}$ . Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside!)

Answer:

The surface of the earth and our body, both are good conductors. So our body and the ground both have the same equipotential surface as we are connected from the ground. When we move outside the house, the equipotential surfaces in the air changes so that our body and ground is kept at the same potential. Therefore we do not get an electric shock.

25. (b) A man fixes outside his house one evening a two metre high insulating slab carrying on its top a large aluminium sheet of area 1m^{2} . Will he get an electric shock if he touches the metal sheet next morning?

Answer:

Yes, the man will get an electric shock. the aluminium sheet is gradually charged up by discharging current of atmosphere. Eventually the voltage will increase up to a certain point depending on the capacitance of the capacitor formed by aluminium sheet, insulating slab and the ground. When the man touches the that charged metal, he will get a shock.

25. c) The discharging current in the atmosphere due to the small conductivity of air is known to be 1800 A on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?

Answer:

Thunderstorm and lightning across the globe keep the atmosphere charged by releasing the light energy, heat energy, and sound energy in the atmosphere. In a way or other, the atmosphere is discharged through regions of ordinary weather. on an average, the two opposing currents are in equilibrium. Hence the atmosphere perpetually remains charged.

25. (d) What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning? (Hint: The earth has an electric field of about 100 $Vm^{-1}$ at its surface in the downward direction, corresponding to a surface charge density = $-10^{-9}Cm^{-2}$ . Due to the slight conductivity of the atmosphere up to about 50 km (beyond which it is good conductor), about + 1800 C is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)

Answer:

Electrical energy, of the atmosphere, is dissipated as light energy which comes from lightning, heat energy and sound energy which comes from the thunderstorm.

Class 12 Physics NCERT Chapter 2: Higher Order Thinking Skills (HOTS) Questions

Q1. The stored energy of a capacitor charged to 100 V, is 1 J. The capacitance of the capacitor is -

Answer:

The energy stored in a capacitor,

$U=\frac{1}{2} C V^2$.

Rearrange the formula to solve for capacitance

$C=\frac{2 U}{V^2}$.

On Substituting the values $U=1 J$ and $V=100 \mathrm{~V}$ into the formula,
$C=\frac{2 \times 1}{100^2}=\frac{2}{10000}=0.0002 \mathrm{~F}$.

The capacitance of the capacitor is $2 \times 10^{-4} \mathrm{~F}$.

Q.2 A capacitor is filled by two dielectric materials equally in two configurations as shown in the figure. The dielectric constants of materials are $k_1=1.25$ and $k_2=2.25$ and the capacitances in two configurations are $C_1$ and $C_2$ respectively, find out the approximate value of $\ \frac {C_1}{C_2}$ when expressed as an integer.

Answer:

The first arrangement is a parallel combination.

$
C_1^{\prime}=\frac{K_1 \varepsilon_0(A / 2)}{d}=\frac{1}{2} \frac{K_1 \varepsilon_0 A}{d}
$

and $C_2^{\prime}=\frac{1}{2} \frac{K_2 \varepsilon_0 A}{d}$

$
C_1=C_1^{\prime}+C_2^{\prime}=\frac{1}{2} \frac{\left(K_1+K_2\right) \varepsilon_0 A}{d}
$

The second arrangement is a series combination:

$
\begin{aligned}
C_1^{\prime \prime} & =\frac{K_1 \varepsilon_0 A}{d / 2}=\frac{2 K_1 \varepsilon_0 A}{d} \\
C_2^{\prime \prime} & =\frac{K_2 \varepsilon_0 A}{d / 2}=\frac{2 K_2 \varepsilon_0 A}{d} \\
\Rightarrow C_2 & =\frac{C_1^{\prime \prime} C_2^{\prime \prime}}{C_1^{\prime \prime}+C_2^{\prime \prime}}=\frac{K_1 K_2}{K_1+K_2} \frac{2 \varepsilon_0 A}{d} \\
\Rightarrow \frac{C_1}{C_2} & =\frac{\left(K_1+K_2\right)^2}{4 K_1 K_2}=\frac{49}{48}
\end{aligned}
$

The approximate value of $\frac{49}{48}$ when expressed as an integer is 1.

Q.3 Two equal charges $q$ are placed at a distance of 2 a and a third charge -2q is placed at the midpoint. The potential energy of the system is -

Answer:

Potential energy -
$\begin{aligned} & U=\frac{1}{4 \pi \epsilon_0} \frac{q(-2 q)}{a}+\frac{1}{4 \pi \epsilon_0} \frac{q(-2 q)}{a}+\frac{1}{4 \pi \epsilon_0} \frac{q q}{2 q} \\ & =\frac{1}{4 \pi \sigma_0} \frac{\mathrm{q}^2}{a}\left[-2-2+\frac{1}{2}\right] \\ & U=\frac{1}{4 \pi \epsilon_0} \frac{\mathrm{q}^2}{\mathrm{a}}\left(-\frac{7}{2}\right)=-\frac{7 \mathrm{q}^2}{8 \pi \epsilon_0 \mathrm{a}}\end{aligned}$

Q.4 Twenty-seven drops of water of the same size are equally and similarly changed. They are then united to form a bigger drop. By what factor will the electrical potential change?

A) 9 times

B) 27 times

C) 6 times

D) 3 times
Answer:

Let $V_B$ is the potential of a bigger drop and $V_S$ potential of a small drop.

$
\text { use, } V_B=n^{2 / 3} V_s \quad-(1)
$

but $n=27$. put in (1) we get-

$
\begin{aligned}
& V_B=(27)^{2 / 3} V_s \\
& V_B=\left(3^3\right)^{2 / 3} V_s=3^2 V_s \\
& V_B=9 V_S \rightarrow 9 \text { times }
\end{aligned}
$

Hence, the answer is the option 1.

Q.5 Find the total charge (in $\mu C$) stored in the network of capacitors connected between A and B as shown in figure :

Answer:

The given circuit is a balanced bridge. Total capacitance

$\begin{aligned} & C=\frac{2 \times 4}{2+4}+\frac{6 \times 3}{6+3} \\ & =\frac{4}{3}+2=\frac{10}{3} \mu F \\ & Q=C V=\frac{10}{3} \mu F \times 3 V=10 \mu C\end{aligned}$

Hence, the answer is 10.