NCERT solutions for Class 12 Physics Chapter 6 - Electromagnetic Induction
Ever wondered how electric generators produce electricity or how a changing magnetic field induces current? That is the magic of Electromagnetic Induction. The Class 12 Physics Chapter 6 Solutions help you to master this topic with clear explanations for every concept and question. These Electromagnetic Induction Class 12 NCERT solutions make the tough theory and numericals simple and very easy.
Candidates will be awarded four marks for each correct answer, whereas one mark will be deducted for each wrong response. Notably, no marks will be deducted for unanswered questions.
This Story also Contains
- NCERT Solution for Class 12 Physics Chapter 6 Solutions: Download Solution PDF :
- Class 12 Physics Electromagnetic Induction Chapter: Exercise Questions
- NCERT Solutions for Class 12 Physics Chapter 6: Additional questions
- Class 12 Physics NCERT Chapter 6: Higher Order Thinking Skills (HOTS) Questions
- NCERT Class 12 Physics Chapter 6 Electromagnetic Induction: Important Topics
- Electromagnetic Induction Class 12: Important Formula
- Approach to Solve Questions of Electromagnetic Induction Class 12
- What Extra Should Students Study Beyond NCERT for JEE/NEET?
- Importance of NCERT Solutions for Class 12 Physics Chapter 6 in Exams
- NCERT Solutions for Class 12 Physics: Chapter-Wise

The NCERT solution for Class 12 Physics Electromagnetic Induction Chapter is essential for competitive tests like JEE and NEET, in addition to Class 12 exams, and helps in understanding its fundamentals, which makes it easier to understand how many of the gadgets we use on a daily basis—from big power systems to home appliances—operate. Essential information on how changing magnetic fields can produce electric currents, which power the technology that runs our world, is provided in the NCERT solutions Class 12 Physics of electromagnetic induction.
NCERT Solution for Class 12 Physics Chapter 6 Solutions: Download Solution PDF :
NCERT Solutions for Class 12 Physics Chapter 6: Electromagnetic Induction help in understanding well the phenomenon of how a changing magnetic field generates electrical currents. This article contains step-wise solutions to NCERT questions that help a student not only master a concept but also develop the skill of solving problems. You may also download a free PDF to revise at any time and prepare well in advance of board exams, JEE and NEET.
Class 12 Physics Electromagnetic Induction Chapter: Exercise Questions
The Exercise Questions of Class 12 Physics Chapter 6 – Electromagnetic Induction are designed to test conceptual understanding and application of Faraday’s law, Lenz’s law, and induced EMF. Solving these NCERT exercises helps students build strong analytical skills and prepares them well for board exams as well as competitive exams like JEE and NEET.
Q 6.1(a) Predict the direction of induced current in the situations described by the following
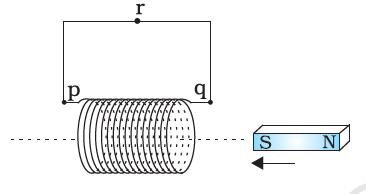
Answer:
To oppose the magnetic field current should flow in anti-clockwise, so the direction of the induced current is qrpq
Q 6.1 (b) Predict the direction of induced current in the situations described by the following Figs.
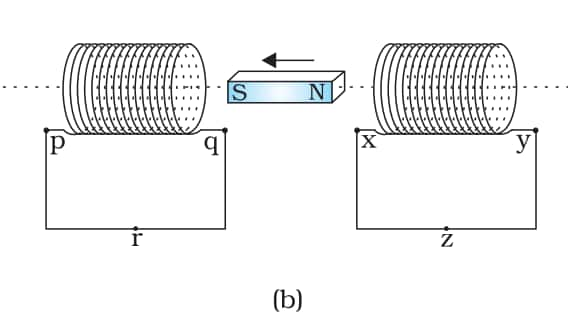
Answer:
Current in the wire in a way such that it opposes the change in flux through the loop. Here hence current will induce in the direction of p--->r--->q in the first coil and y--->z--->x in the second coil.
Q 6.1 (c) Predict the direction of induced current in the situations described by the following Figs.(c)
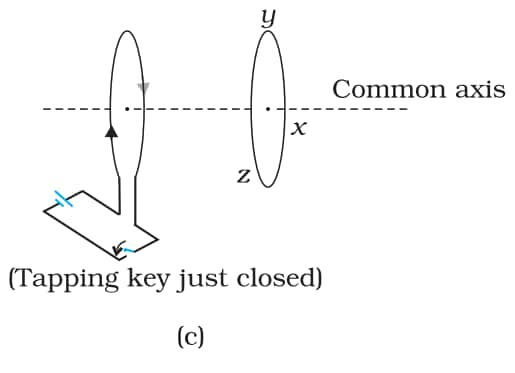
Answer:
When we close the key, the current will flow through the first loop, and suddenly, magnetic flux will pass through it such that the magnetic field will go from right to left of the first loop. Now, to oppose this change, current in the second loop will flow such that magnetic fields go from left to right, which is the direction yzxy
Q 6.1 (d) Predict the direction of induced current in the situations described by the following Fig. (d)
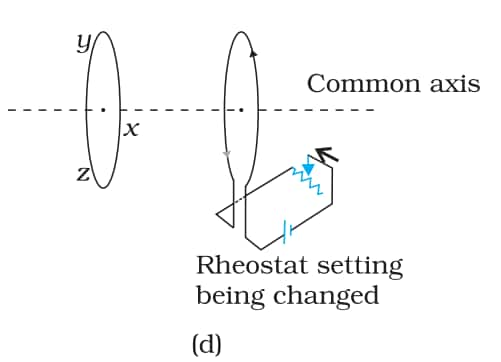
Answer:
When we increase the resistance of the rheostat, the current will decrease, which means flux will decrease, so current will be induced to increase the flux through it. Flux will increase if current flows in xyzx.
On the other hand, if we decrease the resistance, that will increase the current, which means flux will increase, so the current will induce to reduce the flux. Flux will be reduced if the current goes in the direction zyxz
Q 6.1 (e) Predict the direction of induced current in the situations described by the following Fig(e)
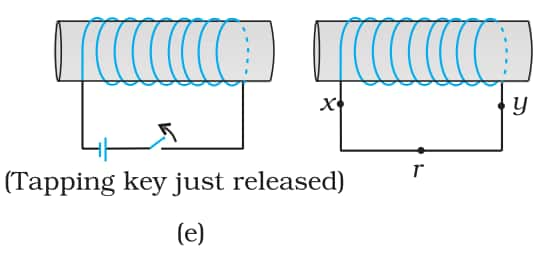
Answer:
As we release the tapping key, current will induce to increase in the flux. Flux will increase when current flows in the direction xryx.
Q 6.1 (f) Predict the direction of induced current in the situations described by the following Fig (f)
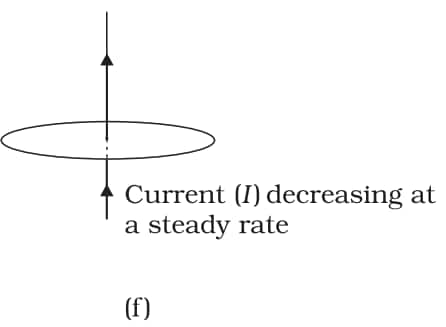
Answer:
The current will not induce as the magnetic field lines are parallel to the plane. In other words, since flux through the loop is constant (zero in fact), there won't be any induction of the current.
Q6.2 (a) Use Lenz’s law to determine the direction of induced current in the situations described by Fig. : a
A wire of irregular shape turning into a circular shape;

Answer:
By turning the wire from an irregular shape to a circle, we are increasing the area of the loop, so flux will increase and current will be induced in such a way that reduces the flux through it. By the right-hand thumb rule direction of current is adcba.
Q6.2 (b) Use Lenz’s law to determine the direction of induced current in the situations described by Fig. b :
A circular loop being deformed into a narrow straight wire.

Answer:
Here, by changing shape, we are decreasing the area or decreasing the flux, so the current will be induced in a manner such that it increases the flux. Since the magnetic field is coming out of the plane, the direction of the current will be adcba.
Q6.3 A long solenoid with
Answer:
Given in a solenoid,
The number of turns per unit length :
loop area :
Current in the solenoid :
Initial current =
Finalcurrent =
Change in current :
Change in time:
Now, the induced emf :
Hence induced emf in the loop is
Answer:
Given:
Length of rectangular loop :
Width of the rectangular loop:
Area of the rectangular loop:
Strength of the magnetic field
The velocity of the loop :
Now,
a) Induced emf in the long side wire of the rectangle:
This EMF will be induced till the loop gets out of the magnetic field, so the time for which the EMF will be induced:
Hence, a
b) Induced emf when we move along the width of the rectangle:
time for which the emf will induce :
Hence, a
Answer:
Given
length of metallic rod :
Angular frequency of rotation :
Magnetic field (which is uniform)
Velocity: here velocity at each point of the rod is different. One end of the rod has zero velocity, and the other end has velocity
Hence, we take the average velocity of the rod, so,
Average velocity
Now,
Induce emf
Hence emf developed is 100V.
Answer:
Given
Length of the wire
Speed of the wire
The magnetic field of the earth
Now,
The instantaneous value of induced emf :
Hence instantaneous emf induced is
Answer:
If we apply Fleming's right-hand rule, we see that the direction of the induced emf is from west to east.
Answer:
The eastern wire will be at the higher potential end.
Answer:
Given
Initial current
Final current
Change in time
Average emf
Now,
As we know, in an inductor
Hence self-inductance of the circuit is 4H.
Answer:
Given
Mutual inductance between two coils:
Currents in a coil:
Change in current:
The time taken for the change
The relation between emf and mutual inductance:
Hence, the change in flux in the coil is
NCERT Solutions for Class 12 Physics Chapter 6: Additional questions
The Additional Questions of Class 12 Physics Chapter 6 Electromagnetic Induction offer extra practice outside of the textbook, centring on problems and application-oriented learning. These questions enhance the conceptual clarity of the topics such as mutual induction, eddy currents, and the generation of an alternating current, which are of great value for the board exams and entrance exams like JEE and NEET.
Answer:
Given
Speed of the plane:
Earth's magnetic field at that location:
The angle of dip is the angle made with the horizontal by Earth's magnetic field:
Length of the wings
Now, since only the vertical component of the magnetic field will cut the wings of the plane perpendicularly, only those will help in inducing an emf.
The vertical component of the Earth's magnetic field :
So now, Induce emf :
Hence voltage difference developed between the ends of the wing is 3.125V.
Answer:
Given,
Area of the rectangular loop which is held still:
The resistance of the loop:
The initial value of the magnetic field :
Rate of decrease of this magnetic field:
Induced emf in the loop :
Induced Current :
The power dissipated in the loop:
The external force, which is responsible for changing the magnetic field, is the actual source of this power.
Answer:
Given,
Side of the square loop
Area of the loop:
The resistance of the loop:
The velocity of the loop in the positive x-direction
The gradient of the magnetic field in the negative x-direction
Rate of decrease of magnetic field intensity
Now, here emf is being induced by means of both changing the magnetic field with time and changing with space. So let us find out the emf induced by both the change of space and time, individually.
Induced emf due to a field changing with time:
Induced emf due to a field changing with space:
Now, Total induced emf :
Total induced current :
Since the flux is decreasing, the induced current will try to increase the flux through the loop along the positive z-direction.
Answer:
Given,
Area of search coil :
The resistance of the coil and the galvanometer
The number of turns in the coil:
Charge flowing in the coil
Now.
Induced emf in the search coil
Hence magnetic field strength for the magnet is 0.75T.

Answer:
Given
Length of the rod
Speed of the rod
Strength of the magnetic field
induced emf in the rod
Hence 9mV emf is induced and it is induced in a way such that P is positive and Q is negative.

Answer:
Yes, there will be an excess charge built up at the end of the rod when the key is open. This is because when we move the conductor in a magnetic field, the positive and negative charge particles will experience the force and move into the corners.
When we close the key, these charged particles start moving in the closed loop and a continuous current starts flowing.

Answer:
When the key K is open, there is an excess charge at both ends of the rod. This charged particle creates an electric field between both ends. This electric field exerts an electrostatic force on the charged particles, which cancels out the force due to the magnetic force. That's why the net force on a charged particle, in this case, is zero.
Q5 (d) Figure shows a metal rod

Answer:
Induced emf = 9mV (calculated in a part of this question)
The resistance of the loop with rod = 9
Induced Current
Now,'
Force on the rod
Hence retarding force when k is closed is

Answer:
Force on the rod
Speed of the rod
Power required to keep moving the rod at the same speed
Hence required power is 9mW.
When the key is open, no power is required to keep the moving rod at the same speed.
Q5(f) Figure shows a metal rod

Answer:
Current in the circuit
The resistance of the circuit
The power which is dissipated as heat
Hence, 9mW of heat is dissipated.
We are moving the rod which induces the current. The external agent through which we are moving our rod is the source of the power.

Answer:
If the magnetic field is parallel to the rail, then the motion of the rod will not cut across the magnetic field lines, and hence no emf will be induced. Hence emf induced is zero in this case.
Answer:
Given
Length of the solenoid
Area of the cross-section of the solenoid
Number of turns in the solenoid
Current flowing in the solenoid
The time interval for which current flows
Now.
Initial flux:
Final flux: since no current is flowing,
Now
Induced emf:
Hence, 6.55V of average back emf is induced.
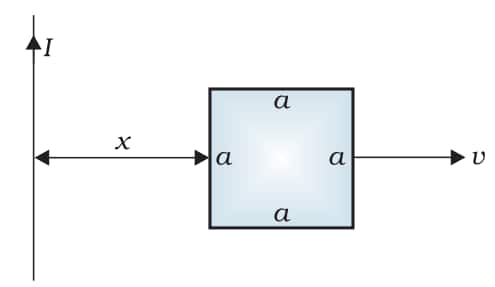
Answer:
Here, let's take a small element dy in the loop at a distance y from the wire
Area of this element dy :
The magnetic field at dy (which is y distance away from the wire)
The magnetic field associated with this element dy
Now, as we know
so
Hence mutual inductance between the wire and the loop is:
Answer:
Given,
Current in the straight wire
Speed of the Loop, which is moving in the right direction
Length of the square loop
Distance from the wire to the left side of the square
Now,
Induced emf in the loop :
Hence emf induced is
What is the angular velocity of the wheel after the field is suddenly switched off?

Answer:
Given,
The radius of the wheel =R
The mass of the wheel = M
Line charge per unit length when the total charge is Q
Magnetic field :
Magnetic force is balanced by centrifugal force when
Angular velocity of the wheel
when
It is the angular velocity of the wheel when the field is suddenly shut off.
Class 12 Physics NCERT Chapter 6: Higher Order Thinking Skills (HOTS) Questions
The HOTS (Higher Order Thinking Skills) questions on Class 12 Physics Chapter 6 - Electromagnetic Induction are aimed at progressing the critical and analytical thinking skills. These tricky questions are beyond simple formulas so that students are ready to implement their knowledge of Faraday's law, Lenz's law, and energy conservation in real life and competitive exam interpretation exercises and JEE and NEET.
Q.1 A conducting circular loop is placed in a uniform magnetic field
a)
b)
c)
d)
Answer:
Hence, the correct option is (2).
Q. 2 At time t=0 magnetic field of 1500 gauss is passing perpendicularly through the area defined by the closed loop shown in the figure. If the magnet's field reduces linearly to 1000 gauss in the next 10 seconds. Then induced FMF in the loop is ____ 
Answer:
Magnetic flux passing through an area is given by
since the film changes linearly,
Hence, the answer is
Q.3 The configuration of a long straight wire and a wire loop with a = 15 cm and b = 20 cm is depicted in Fig. The wire's current fluctuates in accordance with the relationship i = 6t2 – 12 t, where t is measured in seconds and I is in amperes. What is the emf (in 10-7 volts) in the square loop at t = 6 s?
Answer:
The field (due to the current in the long straight wire) through the part of the rectangle above the wire is out of the page (by the right-hand rule), and below the wire, it is into the page. Thus, a strip below the wire (where the strip borders the long wire and reaches a distance of b - a away from it) has exactly the equal but opposite flux that cancels the contribution from the section above the wire, since the height of the part above the wire is b - a.
As per Faraday's law:
So,
Hence, the answer is (26.36)
Q. 4 The self-inductance of a coil having 400 turns is 10 mH. The magnetic flux through the cross-section of the coil corresponding to a current of 2 mA is:
Answer:
Here,
Total magnetic flux linked with the coil,
Magnetic flux through the cross-section of the coil = Magnetic flux linked with each turn
Q.5 Two solenoids of an equal number of turns have their lengths and radii in the same ratio 1:2. The ratio of their self-inductances will be:
Answer:
Self-inductance of solenoids,
Where
NCERT Class 12 Physics Chapter 6 Electromagnetic Induction: Important Topics
The idea of electromagnetic induction is presented in a simple manner in the Class 10 NCERT book. However, a more thorough and in-depth description of electromagnetic induction may be found in Class 12 Physics, Chapter 6. Furthermore, a series of problems and their answers based on the subjects covered in this chapter are provided in the Chapter 6 Physics Class 12 NCERT Solutions. The Class 12 Physics Electromagnetic Induction NCERT Solutions cover questions from the following topics:
- Faraday's Law of Electromagnetic Induction
- Lenz's Law
- Concept of Magnetic Flux
- Electromagnetic Induction and Its Phenomena
- Self-Induction and Mutual Induction
- Time-Varying Magnetic Field and Induced Electric Field
- Eddy Currents
- Motional Electromotive Force
- Applications of Electromagnetic Induction: AC Generator, Transformers
- Alternating Current and Its Relation to Electromagnetic Induction
Electromagnetic Induction Class 12: Important Formula
The important formulas of Class 12 Physics Chapter 6 – Electromagnetic Induction act as quick tools to solve numerical problems effectively. They include key relations from Faraday’s law, Lenz’s law, induced emf, mutual and self-induction, making them essential for board exams as well as JEE and NEET preparation.
1. Faraday's Law of Induction:
Where:
2. Lenz's Law:
States that the direction of the induced current (or EMF) is such that it opposes the change in magnetic flux that produces it.
3. Magnetic Flux:
Where:
4. Self-Induction:
Where:
5. Mutual Induction:
Where:
Approach to Solve Questions of Electromagnetic Induction Class 12
- Start with Faraday's Laws: Learn how changing magnetic fields can produce current. Focus on both laws; they are important in this chapter.
- Know Lenz's Law: "Oppose the change" is Lenz's Law in simple words. Learn how it tells the direction of the induced current.
- Magnetic Flux: It is like how much magnetic field passes through a surface. Learn the formula:
- EMF Formula: Learn how EMF is induced:
The minus sign is from Lenz's Law. - Self-inductance (L): It is when a coil opposes the change in its own current. Formula:
- Mutual Inductance (M): One coil affects another nearby coil by changing current. Formula:
- Practice motion-based induction: Solve problems where a conductor moves in a magnetic field. This type of question usually comes in a competitive exam. Use:
- Solve NCERT & PYQs: Focus on concept-based NCERT questions. Many numerical and theoretical questions come directly from them.
What Extra Should Students Study Beyond NCERT for JEE/NEET?
In addition to NCERT, students looking to appear in JEE/NEET in Electromagnetic Induction should practice in-depth applications such as AC generator, elaborate solutions to mutual and self-inductance, energy in inductors and conceptual problems including Lenz law. Solving higher-level numericals and previous JEE/NEET papers, one can develop good accuracy and speed.
Importance of NCERT Solutions for Class 12 Physics Chapter 6 in Exams
For both the CBSE Class 12 board exams and competitive tests like KVPY, NEET, and JEE Main, the NCERT answers for Class 12 Physics, Chapter 6 on Electromagnetic Induction, are essential.
Determining the direction of induced electromagnetic fields is a typical issue in tests like NEET and JEE Main. The Electromagnetic Induction part of the NCERT answers covers a lot of these difficulties.
The chapters on electromagnetic induction usually account for 10% of the questions on the CBSE board exam.
NCERT Solutions for Class 12 Physics: Chapter-Wise
The NCERT Solutions for Class 12 Physics (Chapter-wise) provide a well-structured approach to mastering every topic as per the latest CBSE curriculum. These step-by-step solutions help students strengthen concepts, practice problem-solving, and prepare effectively for both board exams and competitive exams like JEE and NEET.
Also, check NCERT Books and NCERT Syllabus here:
- NCERT Books Class 12 Physics
- NCERT Syllabus Class 12 Physics
- NCERT Books Class 12
- NCERT Syllabus Class 12
NCERT solutions subject-wise
- NCERT solutions for class 12 mathematics
- NCERT solutions for class 12 chemistry
- NCERT solutions for class 12 physics
- NCERT solutions for class 12 biology
Also, check
NCERT Exemplar Class 12 Solutions
Frequently Asked Questions (FAQs)
The process by which a fluctuating magnetic field creates an electromotive force (EMF) in a conductor is known as electromagnetic induction.
According to Lenz's Law, the induced EMF is in opposition to the magnetic flux change.
For instance, bringing a magnet close to a coil causes current to be induced, which repels the magnet.
Eddy currents are circulating currents induced in conductors by changing magnetic fields.
Applications: Induction heating, magnetic braking, and electric meters.
Yes, the chapter is helpful for higher studies in the field of electronics and electrical engineering-related subjects and for scientific research.
On an average 5 mark questions are asked for CBSE board exams. Follow the NCERT syllabus and NCERT book for a good score in the board exam. Along with the NCERT solutions exercises can also practice NCERT exemplar problems and CBSE board previous year papers.
Questions related to CBSE Class 12th
On Question asked by student community
Hello
You will be able to download the CBSE Previous Year Board Question Papers from our official website, careers360, by using the link given below.
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers
I hope this information helps you.
Thank you.
Hello
You will be able to download the CBSE Pre-Board Class 12 Question Paper 2025-26 from our official website by using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-pre-board-class-12-question-paper-2025-26
I hope this information helps you.
Thank you.
Hello,
Yes, it's completely fine to skip this year's 12th board exams and give them next year as a reporter or private candidate, allowing you to prepare better; the process involves contacting your current school or board to register as a private candidate or for improvement exams during the specified
HELLO,
Yes i am giving you the link below through which you will be able to download the Class 12th Maths Book PDF
Here is the link :- https://school.careers360.com/ncert/ncert-book-for-class-12-maths
Hope this will help you!
Failing in pre-board or selection tests does NOT automatically stop you from sitting in the CBSE Class 12 board exams. Pre-boards are conducted by schools only to check preparation and push students to improve; CBSE itself does not consider pre-board marks. What actually matters is whether your school issues your
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

