NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

Question 1: If a line makes angles $90^{\circ}, 135^{\circ},45^{\circ}$ with the x, y and z-axes respectively, find its direction cosines.

Answer:

Let the direction cosines of the line be l, m, and n.

So, we have

$l = \cos90^{\circ}=0$

$m = \cos135^{\circ}=-\frac{1}{\sqrt2}$

$n= \cos45^{\circ}=\frac{1}{\sqrt2}$

Therefore, the direction cosines of the lines are $0,\ -\frac{1}{\sqrt2}, and\ \ \frac{1}{\sqrt2}$.

Question 2: Find the direction cosines of a line which makes equal angles with the coordinate axes.

Answer:

If the line is making an equal angle with the coordinate axes. Then,

Let the common angle made be $\alpha$ with each coordinate axis.

Therefore, we can write;

$l = \cos \alpha,m= \cos \alpha, and\ n= \cos \alpha$

And as we know the relation, $l^2+m^2+n^2 = 1$

$\Rightarrow \cos^2 \alpha +\cos^2 \alpha+\cos^2 \alpha = 1$

$\Rightarrow \cos^2 \alpha = \frac{1}{3}$

or $\cos \alpha =\pm \frac{1}{\sqrt3}$

Thus the direction cosines of the line are $\pm \frac{1}{\sqrt3},\ \pm \frac{1}{\sqrt3},and\ \pm \frac{1}{\sqrt3}$

Question 3: If a line has the direction ratios –18, 12, – 4, then what are its direction cosines?

Answer:

Given a line has direction ratios of -18, 12, – 4, then its direction cosines are;

A line having direction ratio -18 has direction cosine:

$\frac{-18}{\sqrt{(-18)^2+(12)^2+(-4)^2}} = \frac{-18}{22} = \frac{-9}{11}$

A line having direction ratio 12 has direction cosine:

$\frac{12}{\sqrt{(-18)^2+(12)^2+(-4)^2}} = \frac{12}{22} =\frac{6}{11}$

A line having direction ratio -4 has direction cosine:

$\frac{12}{\sqrt{(-4)^2+(12)^2+(-4)^2}} = \frac{-4}{22} = \frac{-2}{11}$

Thus, the direction cosines are $\frac{-9}{11},\ \frac{6}{11},\ \frac{-2}{11}$ .

Question 4: Show that the points (2, 3, 4), (– 1, – 2, 1), (5, 8, 7) are collinear.

Answer:

We have the points, A (2, 3, 4), B (– 1, – 2, 1), C (5, 8, 7);

And as we can find the direction ratios of the line joining the points $(x_{1},y_{1},z_{1}) \ and\ (x_{2},y_{2},z_{2})$ is given by $x_{2}-x_{1}, y_{2}-y_{1}, \ and\ z_{2}-z_{1}.$

The direction ratios of AB are $(-1-2), (-2-3),\ and\ (1-4)$
i.e., $-3,\ -5,\ and\ -3$

The direction ratios of BC are $(5-(-1)), (8-(-2)),\ and\ (7-1)$
i.e., $6,\ 10,\ and\ 6$ .

We can see that the direction ratios of AB and BC are proportional to each other and are -2 times.

$\therefore$ AB is parallel to BC, and as point B is common to both AB and BC,

Hence, points A, B, and C are collinear.

Question 5: Find the direction cosines of the sides of the triangle whose vertices are (3, 5, – 4), (– 1, 1, 2) and (– 5, – 5, – 2).

Answer:

Given the vertices of the triangle $\triangle ABC$ (3, 5, – 4), (– 1, 1, 2) and (– 5, – 5, – 2).

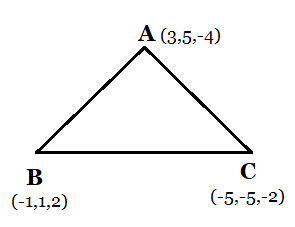
Finding each side direction ratios;

$\Rightarrow$ Direction ratios of side AB are $(-1-3), (1-5),\ and\ (2-(-4))$ i.e.,

$-4,-4,\ and\ 6.$

Therefore, its direction cosines values are;

$\frac{-4}{\sqrt{(-4)^2+(-4)^2+(6)^2}},\ \frac{-4}{\sqrt{(-4)^2+(-4)^2+(6)^2}},\ \frac{6}{\sqrt{(-4)^2+(-4)^2+(6)^2}}$ $or\ \frac{-4}{2\sqrt{17}},\frac{-4}{2\sqrt{17}},\frac{6}{2\sqrt{17}}\ or\ \frac{-2}{\sqrt{17}},\frac{-2}{\sqrt{17}},\frac{3}{\sqrt{17}}$

Similarly, for side BC;

$\Rightarrow$ Direction ratios of side BC are $(-5-(-1)), (-5-1),\ and\ (-2-2)$ i.e.,

$-4,-6,\ and\ -4.$

Therefore, its direction cosines values are;

$\frac{-4}{\sqrt{(-4)^2+(-6)^2+(-4)^2}},\ \frac{-6}{\sqrt{(-4)^2+(-6)^2+(-4)^2}},\ \frac{-4}{\sqrt{(-4)^2+(-6)^2+(-4)^2}}$ $or\ \frac{-4}{2\sqrt{17}},\frac{-6}{2\sqrt{17}},\frac{-4}{2\sqrt{17}}\ or\ \frac{-2}{\sqrt{17}},\frac{-3}{\sqrt{17}},\frac{-2}{\sqrt{17}}$

$\Rightarrow$ Direction ratios of side CA are $(-5-3), (-5-5),\ and\ (-2-(-4))$ i.e.,

$-8,-10,\ and\ 2.$

Therefore, its direction cosines values are;

$\frac{-8}{\sqrt{(-8)^2+(10)^2+(2)^2}},\ \frac{-5}{\sqrt{(-8)^2+(10)^2+(2)^2}},\ \frac{2}{\sqrt{(-8)^2+(10)^2+(2)^2}}$ $or\ \frac{-8}{2\sqrt{42}},\frac{-10}{2\sqrt{42}},\frac{2}{2\sqrt{42}}\ or\ \frac{-4}{\sqrt{42}},\frac{-5}{\sqrt{42}},\frac{1}{\sqrt{42}}$

Question 1: Show that the three lines with direction cosines

$\frac{12}{13},\frac{-3}{13},\frac{-4}{13};\frac{4}{13},\frac{12}{13},\frac{3}{13};\frac{3}{13},\frac{-4}{13},\frac{12}{13}$ are mutually perpendicular.

Answer:

Given direction cosines of the three lines;

$L_{1}\ \left ( \frac{12}{13}, \frac{-3}{13},\frac{-4}{13} \right )$ $L_{2}\ \left ( \frac{4}{13}, \frac{12}{13},\frac{3}{13} \right )$ $L_{3}\ \left ( \frac{3}{13}, \frac{-4}{13},\frac{12}{13} \right )$

And we know that two lines with direction cosines $l_{1},m_{1},n_{1}$ and $l_{2},m_{2},n_{2}$ are perpendicular to each other, if $l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}=0$

Hence, we will check each pair of lines:

Lines $L_{1}\ and\ L_{2}$ ;

$l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}= \left [ \frac{12}{13}\times\frac{4}{13} \right ]+\left [ \frac{-3}{13}\times\frac{12}{13} \right ]+\left [ \frac{-4}{13}\times \frac{3}{13} \right ]$

$\Rightarrow$$ \left [ \frac{48}{169} \right ]-\left [ \frac{36}{169} \right ]-\left [ \frac{12}{169} \right ]= 0$

$\therefore$ the lines $L_{1}\ and\ L_{2}$ are perpendicular.

Lines $L_{2}\ and\ L_{3}$ ;

$l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}= \left [ \frac{4}{13}\times\frac{3}{13} \right ]+\left [ \frac{12}{13}\times\frac{-4}{13} \right ]+\left [ \frac{3}{13}\times \frac{12}{13} \right ]$

$\Rightarrow$$ \left [ \frac{12}{169} \right ]-\left [ \frac{48}{169} \right ]+\left [ \frac{36}{169} \right ]= 0$

$\therefore$ the lines $L_{2}\ and\ L_{3}$ are perpendicular.

Lines $L_{3}\ and\ L_{1}$ ;

$l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2}= \left [ \frac{3}{13}\times\frac{12}{13} \right ]+\left [ \frac{-4}{13}\times\frac{-3}{13} \right ]+\left [ \frac{12}{13}\times \frac{-4}{13} \right ]$

$\Rightarrow$$ \left [ \frac{36}{169} \right ]+\left [ \frac{12}{169} \right ]-\left [ \frac{48}{169} \right ]= 0$

$\therefore$ the lines $L_{3}\ and\ L_{1}$ are perpendicular.

Thus, we have all lines that are mutually perpendicular to each other.

Question 2: Show that the line through the points (1, – 1, 2), (3, 4, – 2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).

Answer:

We have given points where the line passes through it.

Consider the line joining the points (1, – 1, 2) and (3, 4, – 2) is AB, and the line joining the points (0, 3, 2) and (3, 5, 6) is CD.

So, we will find the direction ratios of the lines AB and CD;

Direction ratios of AB are $a_{1},b_{1}, c_{1}$

$(3-1),\ (4-(-1)),\ and\ (-2-2)$ or $2,\ 5,\ and\ -4$

Direction ratios of CD are $a_{2},b_{2}, c_{2}$

$(3-0),\ (5-3)),\ and\ (6-2)$ or $3,\ 2,\ and\ 4$ .

Now, lines AB and CD will be perpendicular to each other if $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} =0$

$\Rightarrow$$a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} =\left ( 2\times3 \right ) +\left ( 5\times2 \right )+ \left ( -4\times 4 \right )$

$\Rightarrow$$ 6+10-16 = 0$

Therefore, AB and CD are perpendicular to each other.

Question 3: Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (– 1, – 2, 1), (1, 2, 5).

Answer:

We have given points where the line passes through them.

Consider the line joining the points (4, 7, 8) and (2, 3, 4) is AB and the line joining the points (– 1, – 2, 1) and (1, 2, 5) is CD.

So, we will find the direction ratios of the lines AB and CD;

Direction ratios of AB are $a_{1},b_{1}, c_{1}$

$(2-4),\ (3-7),\ and\ (4-8)$ or $-2,\ -4,\ and\ -4$

Direction ratios of CD are $a_{2},b_{2}, c_{2}$

$(1-(-1)),\ (2-(-2)),\ and\ (5-1)$ or $2,\ 4,\ and\ 4$ .

Now, lines AB and CD will be parallel to each other if $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$

Therefore, we have now;

$\frac{a_{1}}{a_{2}} = \frac{-2}{2}=-1$ $\frac{b_{1}}{b_{2}} = \frac{-4}{4}=-1$ $\frac{c_{1}}{c_{2}} = \frac{-4}{4}=-1$

$\therefore \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}$

Hence, we can say that AB is parallel to CD.

Question 4: Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector $3\widehat{i}+2\widehat{j}-2\widehat{k}$.

Answer:

It is given that the line is passing through A (1, 2, 3) and is parallel to the vector $\vec{b}=3\widehat{i}+2\widehat{j}-2\widehat{k}$

We can easily find the equation of the line which passes through the point A and is parallel to the vector $\vec{b}$ by the known relation;

$\vec{r} = \vec{a} +\lambda\vec{b}$ , where $\lambda$ is a constant.

So, we have now,

$\\\mathrm{\Rightarrow\vec{r}=\widehat{i}+2\widehat{j}+3\widehat{k} + \lambda(3\widehat{i}+2\widehat{j}-2\widehat{k})}$

Thus, the required equation of the line.

Question 5: Find the equation of the line in vector and in cartesian form that passes through the point with position vector $2\widehat{i}-\widehat{j}+4\widehat{k}$ and is in the direction $\widehat{i}+2\widehat{j}-\widehat{k}$.

Answer:

Given that the line is passing through the point with position vector $2\widehat{i}-\widehat{j}+4\widehat{k}$ and is in the direction of the line $\widehat{i}+2\widehat{j}-\widehat{k}$.

And we know the equation of the line which passes through the point with the position vector $\vec{a}$ and parallel to the vector $\vec{b}$ is given by the equation,

$\vec{r} = \vec{a} +\lambda\vec{b}$

$\Rightarrow\vec{r}=2\widehat{i}-\widehat{j}+4\widehat{k} + \lambda(\widehat{i}+2\widehat{j}-\widehat{k})$

So, this is the required equation of the line in the vector form.

$\vec{r} =x\widehat{i}+y\widehat{j}+z\widehat{k} = (\lambda+2)\widehat{i}+(2\lambda-1)\widehat{j}+(-\lambda+4)\widehat{k}$

Eliminating $\lambda$, from the above equation, we obtain the equation in the Cartesian form :

$\frac{x-2}{1}= \frac{y+1}{2} =\frac{z-4}{-1}$

Hence, this is the required equation of the line in Cartesian form.

Question 6: Find the cartesian equation of the line which passes through the point (– 2, 4, – 5) and parallel to the line given by $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$.

Answer:

Given a line which passes through the point (– 2, 4, – 5) and is parallel to the line given by the $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$ ;

The direction ratios of the line, $\frac{x+3}{3}=\frac{y-4}{5}=\frac{z+8}{6}$ are 3,5 and 6 .

So, the required line is parallel to the above line.

Therefore, we can take the direction ratios of the required line as 3k, 5k, and 6k, where k is a non-zero constant.

And we know that the equation of line passing through the point $(x_{1},y_{1},z_{1})$ and with direction ratios a, b, c is written by: $\frac{x-x_{1}}{a} = \frac{y-y_{1}}{b} = \frac{z-z_{1}}{c}$.

Therefore, we have the equation of the required line:

$\frac{x+2}{3k} = \frac{y-4}{5k} = \frac{z+5}{6k}$

or $\frac{x+2}{3} = \frac{y-4}{5} = \frac{z+5}{6} = k$

The required line equation.

Question 7: The cartesian equation of a line is $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{7}$ . Write its vector form.

Answer:

Given the Cartesian equation of the line;

$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{7}$

Here, the given line is passing through the point $(5,-4,6)$.

So, we can write the position vector of this point as;

$\vec{a} = 5\widehat{i}-4\widehat{j}+6\widehat{k}$

And the direction ratios of the line are 3, 7, and 2.

This implies that the given line is in the direction of the vector, $\vec{b} = 3\widehat{i}+7\widehat{j}+2\widehat{k}$.

Now, we can easily find the required equation of the line:

As we know, the line passing through the position vector $\vec{a}$ and in the direction of the vector $\vec{b}$ is given by the relation,

$\vec{r} = \vec{a} + \lambda \vec{b},\ \lambda \epsilon R$

So, we get the equation.

$\vec{r}=5\widehat{i}-4\widehat{j}+6\widehat{k}+\lambda(3\widehat{i}+7\widehat{j}+2\widehat{k}),\ \lambda \epsilon R$

This is the required equation of the line in the vector form.

Question 8: Find the angle between the following pairs of lines:

(i)$\overrightarrow{r}=2\widehat{i}-5\widehat{j}+\widehat{k}+\lambda (3\widehat{i}+2\widehat{j}+6\widehat{k})$ and $\overrightarrow{r}=7\widehat{i}-6\widehat{k}+\mu (\widehat{i}+2\widehat{j}+2\widehat{k})$

(ii) $\overrightarrow{r}= 3\widehat{i}+\widehat{j}-2\widehat{k}+\lambda (\widehat{i}-\widehat{j}-2\widehat{k})$ and $\overrightarrow{r}=2\widehat{i}-\widehat{j}-56\widehat{k}+\mu (3\widehat{i}-5\widehat{j}-4\widehat{k})$

Answer:

(i) To find the angle A between the pair of lines $\vec{b_{1}}\ and\ \vec{b_{2}}$, we have the formula;

$\cos A = \left | \frac{\vec{b_{1}}.\vec{b_{2}}}{|\vec{b_{1}}||\vec{b_{2}}|} \right |$

We have two lines :

$\overrightarrow{r}=2\widehat{i}-5\widehat{j}+\widehat{k}+\lambda (3\widehat{i}+2\widehat{j}+6\widehat{k})$ and

$\overrightarrow{r}=7\widehat{i}-6\widehat{k}+\mu (\widehat{i}+2\widehat{j}+2\widehat{k})$

The given lines are parallel to the vectors $\vec{b_{1}}\ and\ \vec{b_{2}}$ ;

where $\vec{b_{1}}= 3\widehat{i}+2\widehat{j}+6\widehat{k}$ and $\vec{b_{2}}= \widehat{i}+2\widehat{j}+2\widehat{k}$ respectively,

Then we have

$\vec{b_{1}}.\vec{b_{2}}=(3\widehat{i}+2\widehat{j}+6\widehat{k}).(\widehat{i}+2\widehat{j}+2\widehat{k})$

$=3+4+12 = 19$

and $|\vec{b_{1}}| = \sqrt{3^2+2^2+6^2} = 7$

$|\vec{b_{2}}| = \sqrt{1^2+2^2+2^2} = 3$

Therefore, we have;

$\cos A = \left | \frac{19}{7\times3} \right | = \frac{19}{21}$

or $A = \cos^{-1} \left ( \frac{19}{21} \right )$

(ii) To find the angle A between the pair of lines $\vec{b_{1}}\ and\ \vec{b_{2}}$, we have the formula;

$\cos A = \left | \frac{\vec{b_{1}}.\vec{b_{2}}}{|\vec{b_{1}}||\vec{b_{2}}|} \right |$

We have two lines :

$\overrightarrow{r}=3\widehat{i}+\widehat{j}-2\widehat{k}+\lambda(\widehat{i}-\widehat{j}-2\widehat{k})$ and

$\overrightarrow{r}=2\widehat{i}-\widehat{j}-56\widehat{k}+\mu (3\widehat{i}-5\widehat{j}-4\widehat{k})$

The given lines are parallel to the vectors $\vec{b_{1}}\ and\ \vec{b_{2}}$ ;

where $\vec{b_{1}}= \widehat{i}-\widehat{j}-2\widehat{k}$ and $\vec{b_{2}}= 3\widehat{i}-5\widehat{j}-4\widehat{k}$ respectively,

Then we have

$\vec{b_{1}}.\vec{b_{2}}=(\widehat{i}-\widehat{j}-2\widehat{k}).(3\widehat{i}-5\widehat{j}-4\widehat{k})$

$=3+5+8 = 16$

and $|\vec{b_{1}}| = \sqrt{1^2+(-1)^2+(-2)^2} = \sqrt{6}$

$|\vec{b_{2}}| = \sqrt{3^2+(-5)^2+(-4)^2} = \sqrt{50} = 5\sqrt2$

Therefore, we have;

$\cos A = \left | \frac{16}{\sqrt6 \times5\sqrt2} \right | = \frac{16}{10\sqrt3}$

or $A = \cos^{-1} \left ( \frac{8}{5\sqrt3} \right )$

Question 9: Find the angle between the following pair of lines:

(i) $\frac{x-2}{2}= \frac{y-1}{5}= \frac{z+3}{-3}$ and $\frac{x+2}{-1}= \frac{y-4}{8}= \frac{z-5}{4}$

(ii) $\frac{x}{2}= \frac{y}{2}=\frac{z}{1}$ and $\frac{x -5}{4}= \frac{y-2}{1}=\frac{z-3}{8}$

Answer:

(i) Given lines are;

$\frac{x-2}{2}= \frac{y-1}{5}= \frac{z+3}{-3}$ and $\frac{x+2}{-1}= \frac{y-4}{8}= \frac{z-5}{4}$

So, we have two vectors $\vec{b_{1}}\ and\ \vec{b_{2}}$, which are parallel to the pair of above lines respectively.

$\vec{b_{1}}\ =2\widehat{i}+5\widehat{j}-3\widehat{k}$ and $\vec{b_{2}}\ =-\widehat{i}+8\widehat{j}+4\widehat{k}$

To find the angle A between the pair of lines $\vec{b_{1}}\ and\ \vec{b_{2}}$ we have the formula;

$\cos A = \left | \frac{\vec{b_{1}}.\vec{b_{2}}}{|\vec{b_{1}}||\vec{b_{2}}|} \right |$

Then we have

$\vec{b_{1}}.\vec{b_{2}}=(2\widehat{i}+5\widehat{j}-3\widehat{k}).(-\widehat{i}+8\widehat{j}+4\widehat{k})$

$=-2+40-12 = 26$

and $|\vec{b_{1}}| = \sqrt{2^2+5^2+(-3)^2} = \sqrt{38}$

$|\vec{b_{2}}| = \sqrt{(-1)^2+(8)^2+(4)^2} = \sqrt{81} = 9$

Therefore, we have;

$\cos A = \left | \frac{26}{\sqrt{38} \times9} \right | = \frac{26}{9\sqrt{38}}$

or $A = \cos^{-1} \left ( \frac{26}{9\sqrt{38}} \right )$

(ii) Given lines are;

$\frac{x}{2}= \frac{y}{2}=\frac{z}{1}$ and $\frac{x -5}{4}= \frac{y-2}{1}=\frac{z-3}{8}$

So, we have two vectors $\vec{b_{1}}\ and\ \vec{b_{2}}$ which are parallel to the pair of above lines respectively.

$\vec{b_{1}}\ =2\widehat{i}+2\widehat{j}+\widehat{k}$ and $\vec{b_{2}}\ =4\widehat{i}+\widehat{j}+8\widehat{k}$

To find the angle A between the pair of lines $\vec{b_{1}}\ and\ \vec{b_{2}}$ we have the formula;

$\cos A = \left | \frac{\vec{b_{1}}.\vec{b_{2}}}{|\vec{b_{1}}||\vec{b_{2}}|} \right |$

Then we have

$\vec{b_{1}}.\vec{b_{2}}=(2\widehat{i}+2\widehat{j}+\widehat{k}).(4\widehat{i}+\widehat{j}+8\widehat{k})$

$=8+2+8 = 18$

and $|\vec{b_{1}}| = \sqrt{2^2+2^2+1^2} = \sqrt{9} = 3$

$|\vec{b_{2}}| = \sqrt{(4)^2+(1)^2+(8)^2} = \sqrt{81} = 9$

Therefore, we have;

$\cos A = \left | \frac{18}{ 3\times9} \right | = \frac{2}{3}$

or $A = \cos^{-1} \left ( \frac{2}{3} \right )$

Question 10: Find the values of p so that the lines $\frac{1-x}{3}=\frac{7y-14}{2p}= \frac{z-3}{2}$ and $\frac{7-7x}{3p}=\frac{y-5}{1}= \frac{6-z}{5}$ are at right angles.

Answer:

First, we have to write the given equation of lines in the standard form.

$\frac{x-1}{-3}=\frac{y-2}{\frac{2p}{7}}= \frac{z-3}{2}$ and $\frac{x-1}{\frac{-3p}{7}}=\frac{y-5}{1}= \frac{z-6}{-5}$

Then we have the direction ratios of the above lines as;

$-3,\ \frac{2p}{7},\ 2$ and $\frac{-3p}{7},\ 1,\ -5$ respectively..

Two lines with direction ratios $a_{1},b_{1},c_{1}$ and $a_{2},b_{2},c_{2}$ are perpendicular to each other if, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}= 0$

$\therefore (-3).\left ( \frac{-3p}{7} \right )+(\frac{2p}{7}).(1) + 2.(-5) = 0$

$\Rightarrow \frac{9p}{7}+ \frac{2p}{7} =10$

$\Rightarrow 11p =70$

$\Rightarrow p =\frac{70}{11}$

Thus, the value of p is $\frac{70}{11}$.

Question 11: Show that the lines $\frac{x-5}{7}=\frac{y+2}{-3}=\frac{z}{1}$ and $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$ are perpendicular to each other.

Answer:

First, we have to write the given equation of lines in the standard form.

$\frac{x-5}{7}=\frac{y+2}{-5}=\frac{z}{1}$ and $\frac{x}{1}=\frac{y}{2}=\frac{z}{3}$

Then we have the direction ratios of the above lines as;

$7,\ -5,\ 1$ and $1,\ 2,\ 3$ respectively..

Two lines with direction ratios $a_{1},b_{1},c_{1}$ and $a_{2},b_{2},c_{2}$ are perpendicular to each other if, $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}= 0$

$\therefore 7(1) + (-5)(2)+1(3) = 7-10+3 = 0$

Therefore, the two lines are perpendicular to each other.

Question 12: Find the shortest distance between the lines

$\overrightarrow{r}=(\widehat{i}+2\widehat{j}+\widehat{k})+\lambda (\widehat{i}-\widehat{j}+\widehat{k})$ and $\overrightarrow{r}=(2\widehat{i}-\widehat{j}-\widehat{k})+\mu (2\widehat{i}+\widehat{j}+2\widehat{k})$

Answer:

So given the equation of lines;

$\overrightarrow{r}=(\widehat{i}+2\widehat{j}+\widehat{k})+\lambda(\widehat{i}-\widehat{j}+\widehat{k})$and$\overrightarrow{r}=(2\widehat{i}-\widehat{j}-\widehat{k})+\mu (2\widehat{i}+\widehat{j}+2\widehat{k})$ in the vector form.

Now, we can find the shortest distance between the lines $\vec{r} = \vec{a_{1}}+\lambda\vec{b_{1}}$ and $\vec{r} = \vec{a_{2}}+\mu \vec{b_{2}}$, is given by the formula,

$d= \left | \frac{\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )}{\left | \vec{b_{1}}\times \vec{b_{2}} \right |} \right |$

Now, comparing the values from the equation, we obtain

$\vec{a_{1}}=\widehat{i}+2\widehat{j}+\widehat{k}$$\vec{b_{1}}=\widehat{i}-\widehat{j}+\widehat{k}$

$\vec{a_{2}}=2\widehat{i}-\widehat{j}-\widehat{k}$$\vec{b_{2}} = 2\widehat{i}+\widehat{j}+2\widehat{k}$

$\vec{a_{2}} -\vec{a_{1}} =\left ( 2\widehat{i}-\widehat{j}-\widehat{k} \right ) - \left ( \widehat{i}+2\widehat{j}+\widehat{k} \right ) = \widehat{i}-3\widehat{j}-2\widehat{k}$

Then calculating

$\vec{b_{1}}\times \vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ 1 & -1 &1 \\ 2& 1 &2 \end{vmatrix}$

$\vec{b_{1}}\times \vec{b_{2}} = (-2-1)\widehat{i} - (2-2) \widehat{j} +(1+2) \widehat{k} = -3\widehat{i}+3\widehat{k}$

$\Rightarrow \left | \vec{b_{1}}\times \vec{b_{2}} \right | = \sqrt{(-3)^2+(3)^2} = \sqrt{9+9} =\sqrt{18} =3\sqrt2$

So, substituting the values now in the formula above, we get;

$d =\left | \frac{\left ( -3\widehat{i}+3\widehat{k} \right ).(\widehat{i}-3\widehat{j}-2\widehat{k})}{3\sqrt2} \right |$

$\Rightarrow d = \left | \frac{-3.1+3(-2)}{3\sqrt2} \right |$

$d = \left | \frac{-9}{3\sqrt2} \right | = \frac{3}{\sqrt2} = \frac{3\sqrt2}{2}$

Therefore, the shortest distance between the two lines is $\frac{3\sqrt2}{2}$ units.

Question 13: Find the shortest distance between the lines

$\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ and $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

Answer:

We have given two lines:

$\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ and $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

Calculating the shortest distance between the two lines,

$\frac{x-x_{1}}{a_{1}}=\frac{y-y_{1}}{b_{1}}=\frac{z-z_{1}}{c_{1}}$ and $\frac{x-x_{2}}{a_{2}}=\frac{y-y_{2}}{b_{2}}=\frac{z-z_{2}}{c_{2}}$

by the formula

$d = \frac{\begin{vmatrix} x_{2}-x_{1} &y_{2}-y_{1} &z_{2}-z_{1} \\ a_{1} &b_{1} &c_{1} \\ a_{2}&b_{2} &c_{2} \end{vmatrix}}{\sqrt{(b_{1}c_{2}-b_{2}c_{1})^2+(c_{1}a_{2}-c_{2}a_{1})^2+(a_{1}b_{2}-a_{2}b_{1})^2}}$

Now, comparing the given equations, we obtain

$x_{1} = -1,\ y_{1} =-1,\ z_{1} =-1$

$a_{1} = 7,\ b_{1} =-6,\ c_{1} =1$

$x_{2} = 3,\ y_{2} =5,\ z_{2} =7$

$a_{2} = 1,\ b_{2} =-2,\ c_{2} =1$

Then, calculating the determinant

$\begin{vmatrix} x_{2}-x_{1} &y_{2}-y_{1} &z_{2}-z_{1} \\ a_{1} &b_{1} &c_{1} \\ a_{2}&b_{2} &c_{2} \end{vmatrix} = \begin{vmatrix} 4 &6 &8 \\ 7& -6& 1\\ 1& -2& 1 \end{vmatrix}$

$\Rightarrow$$ 4(-6+2)-6(7-1)+8(-14+6)$

$\Rightarrow$$ -16-36-64$

$\Rightarrow$$-116$

Now, calculating the denominator,

$\sqrt{(b_{1}c_{2}-b_{2}c_{1})^2+(c_{1}a_{2}-c_{2}a_{1})^2+(a_{1}b_{2}-a_{2}b_{1})^2}$

$\Rightarrow$$ \sqrt{(-6+2)^2+(1+7)^2+(-14+6)^2}$ $= \sqrt{16+36+64}$

$ \sqrt{116} = 2\sqrt{29}$

So, we will substitute all the values in the formula above to obtain,

$d = \frac{-116}{2\sqrt{29}} = \frac{-58}{\sqrt{29}} = \frac{-2\times29}{\sqrt{29}} = -2\sqrt{29}$

Since distance is always non-negative, the distance between the given lines is

$2\sqrt{29}$ units.

Question 14: Find the shortest distance between the lines whose vector equations are $\overrightarrow{r}=(\widehat{i}+2\widehat{j}+3\widehat{k})+ \lambda (\widehat{i}-3\widehat{j}+2\widehat{k})$ and

$\overrightarrow{r}=(4\widehat{i}+5\widehat{j}+6\widehat{k})+ \mu (2\widehat{i}+3\widehat{j}+\widehat{k})$

Answer:

Given two equations of a line

$\overrightarrow{r}=(\widehat{i}+2\widehat{j}+3\widehat{k})+\lambda (\widehat{i}-3\widehat{j}+2\widehat{k})$$\overrightarrow{r}=(4\widehat{i}+5\widehat{j}+6\widehat{k})+ \mu (2\widehat{i}+3\widehat{j}+\widehat{k})$ in the vector form.

So, we will apply the distance formula for knowing the distance between two lines $\vec{r} =\vec{a_{1}}+\lambda{b_{1}}$ and $\vec{r} =\vec{a_{2}}+\lambda{b_{2}}$

$d= \left | \frac{\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )}{\left | \vec{b_{1}}\times \vec{b_{2}} \right |} \right |$

After comparing the given equations, we obtain

$\vec{a_{1}}=\widehat{i}+2\widehat{j}+3\widehat{k}$$\vec{b_{1}}= \widehat{i}-3\widehat{j}+2\widehat{k}$

$\vec{a_{2}}=4\widehat{i}+5\widehat{j}+6\widehat{k}$$\vec{b_{2}}= 2\widehat{i}+3\widehat{j}+\widehat{k}$

$\vec{a_{2}}-\vec{a_{1}}=(4\widehat{i}+5\widehat{j}+6\widehat{k})- (\widehat{i}+2\widehat{j}+3\widehat{k})$

$= 3\widehat{i}+3\widehat{j}+3\widehat{k}$

Then, calculate the determinant value of the numerator.

$\vec{b_{1}}\times\vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ 1& -3 &2 \\ 2& 3& 1 \end{vmatrix}$

$=(-3-6)\widehat{i}-(1-4)\widehat{j}+(3+6)\widehat{k}= -9\widehat{i}+3\widehat{j}+9\widehat{k}$

That implies, $\left | \vec{b_{1}}\times\vec{b_{2}} \right | = \sqrt{(-9)^2+(3)^2+(9)^2}$

$= \sqrt{81+9+81} = \sqrt{171} =3\sqrt{19}$

$\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )=(-9\widehat{i}+3\widehat{j}+9\widehat{k})(3\widehat{i}+3\widehat{j}+3\widehat{k})$

$= (-9\times3)+(3\times3)+(9\times3) = 9$

Now, after substituting the value in the above formula, we get,

$d= \left | \frac{9}{3\sqrt{19}} \right | = \frac{3}{\sqrt{19}}$

Therefore, $\frac{3}{\sqrt{19}}$ is the shortest distance between the two given lines.

Question 15: Find the shortest distance between the lines whose vector equations are

$\overrightarrow{r}=(1-t)\widehat{i}+(t-2)\widehat{j}+(3-2t)\widehat{k}$ and $\overrightarrow{r}=(s+1)\widehat{i}+(2s-1)\widehat{j}-(2s+1)\widehat{k}$

Answer:

Given two equations of the line

$\overrightarrow{r}=(1-t)\widehat{i}+(t-2)\widehat{j}+(3-2t)\widehat{k}$ $\overrightarrow{r}=(s+1)\widehat{i}+(2s-1)\widehat{j}-(2s+1)\widehat{k}$ in the vector form.

So, we will apply the distance formula for knowing the distance between two lines $\vec{r} =\vec{a_{1}}+\lambda{b_{1}}$ and $\vec{r} =\vec{a_{2}}+\lambda{b_{2}}$

$d= \left | \frac{\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )}{\left | \vec{b_{1}}\times \vec{b_{2}} \right |} \right |$

After comparing the given equations, we obtain

$\vec{a_{1}}=\widehat{i}-2\widehat{j}+3\widehat{k}$$\vec{b_{1}}=-\widehat{i}+\widehat{j}-2\widehat{k}$

$\vec{a_{2}}=\widehat{i}-\widehat{j}-\widehat{k}$$\vec{b_{2}}= \widehat{i}+2\widehat{j}-2\widehat{k}$

$\vec{a_{2}}-\vec{a_{1}}=(\widehat{i}-\widehat{j}-\widehat{k})- (\widehat{i}-2\widehat{j}+3\widehat{k}) = \widehat{j}-4\widehat{k}$

Then, calculate the determinant value of the numerator.

$\vec{b_{1}}\times\vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ -1& 1 &-2 \\ 1& 2& -2 \end{vmatrix}$

$=(-2+4)\widehat{i}-(2+2)\widehat{j}+(-2-1)\widehat{k}= 2\widehat{i}-4\widehat{j}-3\widehat{k}$

That implies,

$\left | \vec{b_{1}}\times\vec{b_{2}} \right | = \sqrt{(2)^2+(-4)^2+(-3)^2}$

$= \sqrt{4+16+9} = \sqrt{29}$

$\left ( \vec{b_{1}}\times\vec{b_{2}} \right ).\left ( \vec{a_{2}}-\vec{a_{1}} \right )=(2\widehat{i}-4\widehat{j}-3\widehat{k})(\widehat{j}-4\widehat{k}) = -4+12 = 8$

Now, after substituting the value in the above formula, we get,

$d= \left | \frac{8}{\sqrt{29}} \right | = \frac{8}{\sqrt{29}}$

Therefore, $\frac{8}{\sqrt{29}}$ units is the shortest distance between the two given lines.

Question 1: Find the angle between the lines whose direction ratios are a, b, c and b – c, c – a, a – b.

Answer:

Given direction ratios $a,b,c$ and $b-c,\ c-a,\ a-b$ .

Thus, the angle between the lines A is given by;

$A = \left | \frac{a(b-c)+b(c-a)+c(a-b)}{\sqrt{a^2+b^2+c^2}.\sqrt{(b-c)^2+(c-a)^2+(a-b)^2}} \right |$

$\Rightarrow \cos A = 0$

$\Rightarrow A = \cos^{-1}(0) = 90^{\circ}$

Thus, the angle between the lines is $90^{\circ}$.

Question 2: Find the equation of a line parallel to the x-axis and passing through the origin.

Answer:

Equation of a line parallel to the x-axis and passing through the origin $(0,0,0)$ is itself the x-axis.

So, let A be a point on the x-axis.

Therefore, the coordinates of A are given by $(a,0,0)$, where $a\epsilon R$.

Now, the direction ratios of OA are $(a-0) =a,0 , 0$

So, the equation of OA is given by,

$\frac{x-0}{a} = \frac{y-0}{0} = \frac{z-0}{0}$

$\Rightarrow \frac{x}{1} = \frac{y}{0} = \frac{z}{0} = a$

Thus, the equation of the line parallel to the x-axis and passing through the origin is

$\frac{x}{1} = \frac{y}{0} = \frac{z}{0}$

Question 3: If the lines $\frac{x-1}{-3}=\frac{y-2}{k}=\frac{z-3}{2}$ and $\frac{x-1}{3k}=\frac{y-1}{1}=\frac{z-6}{-5}$ are perpendicular, find the value of k.

Answer:

Given both lines are perpendicular so we have the relation; $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

For the two lines whose direction ratios are known,

$a_{1},b_{1},c_{1}\ and\ a_{2},b_{2},c_{2}$

We have the direction ratios of the lines, $\frac{x-1}{-3}=\frac{y-2}{k}=\frac{z-3}{2}$ and $\frac{x-1}{3k}=\frac{y-1}{1}=\frac{z-6}{-5}$ are $-3,2k,2$ and $3k,1,-5$ respectively.

Therefore, applying the formula,

$-3(3k)+2k(1)+2(-5) = 0$

$\Rightarrow -9k +2k -10 = 0$

$\Rightarrow7k=-10$ or $k= \frac{-10}{7}$

$\therefore$ For, $k= \frac{-10}{7}$ the lines are perpendicular.

Question 4: Find,the shortest distance between lines $\overrightarrow{r}=6\widehat{i}+2\widehat{j}+2\widehat{k}+\lambda (\widehat{i}-2\widehat{j}-2\widehat{k})$ and $\overrightarrow{r}=-4\widehat{i}-\widehat{k}+\mu(3\widehat{i}-2\widehat{j}-2\widehat{k})$ .

Answer:

Given lines are;

$\overrightarrow{r}=6\widehat{i}+2\widehat{j}+2\widehat{k}+\lambda (\widehat{i}-2\widehat{j}-2\widehat{k})$ and

$\overrightarrow{r}=-4\widehat{i}-\widehat{k}+\mu(3\widehat{i}-2\widehat{j}-2\widehat{k})$

So, we can find the shortest distance between two lines $\vec{r} = \vec{a_{1}}+\lambda \vec{b_{1}}$ and $\vec{r} = \vec{a_{1}}+\lambda \vec{b_{1}}$ by the formula,

$d = \left | \frac{(\vec{b_{1}}\times\vec{b_{2}}).(\vec{a_{2}}-\vec{a_{1}})}{\left | \vec{b_{1}}\times\vec{b_{2}} \right |} \right |$ ...........................(1)

Now, we have the comparisons of the given equations of lines.

$\vec{a_{1}}=6\widehat{i}+2\widehat{j}+2\widehat{k}$$\vec{b_{1}}= \widehat{i}-2\widehat{j}+2\widehat{k}$

$\vec{a_{2}}=-4\widehat{i}-\widehat{k}$$\vec{b_{2}}= 3\widehat{i}-2\widehat{j}-2\widehat{k}$

So,$\vec{a_{2}}-\vec{a_{1}}=(-4\widehat{i}-\widehat{k})-(6\widehat{i}+2\widehat{j}+2\widehat{k}) = -10\widehat{i}-2\widehat{j}-3\widehat{k}$

and $\Rightarrow \vec{b_{1}}\times \vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ 1 &-2 &2 \\ 3& -2 &-2 \end{vmatrix} = (4+4)\widehat{i}-(-2-6)\widehat{j}+(-2+6)\widehat{k}$

$=8\widehat{i}+8\widehat{j}+4\widehat{k}$

$\therefore \left | \vec{b_{1}}\times \vec{b_{2}} \right | = \sqrt{8^2+8^2+4^2} =12$

$(\vec{b_{1}}\times\vec{b_{2}}).(\vec{a_{2}}-\vec{a_{1}})= (8\widehat{i}+8\widehat{j}+4\widehat{k}).(-10\widehat{i}-2\widehat{j}-3\widehat{k})= -80-16-12 =-108$ Now, substituting all values in equation (3) we get,

$d = | \frac{-108}{12}| = 9$

Hence, the shortest distance between the two given lines is 9 units.

Question 5: Find the vector equation of the line passing through the point (1, 2, – 4) and perpendicular to the two lines:

$\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}$and$\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}$

Answer:

Given

Two straight lines in 3D whose direction cosines are (3,-16,7) and (3,8,-5)

Now, the two vectors which are parallel to the two lines are

$\vec a= 3\hat i-16\hat j+7\hat k$ and

$\vec b= 3\hat i+8\hat j-5\hat k$

As we know, a vector perpendicular to both vectors $\vec a$ and $\vec b$ is $\vec a\times\vec b$ , so

$\vec a\times\vec b=\begin{vmatrix} \hat i &\hat j &\hat k \\ 3& -16 &7 \\ 3&8 &-5 \end{vmatrix}=\hat i(80-56)-\hat j(-15-21)+\hat k(24+48)$

$\vec a\times\vec b=24\hat i+36\hat j+72\hat k$

A vector parallel to this vector is

$\vec d=2\hat i+3\hat j+6\hat k$

Now, as we know, the vector equation of the line which passes through point p and is parallel to vector d is

$L=\vec p+\lambda \vec d$

Here, in our question, give point p = (1,2,-4), which means the position vector of this point is

$\vec p = \hat i +2\hat j-4\hat k$

So, the required line is

$L=\vec p+\lambda \vec d$

$\Rightarrow$$L=\hat i+2\hat j-4\hat k +\lambda (2\hat i+3\hat j+6\hat k)$

$\Rightarrow$$L=(2\lambda +1)\hat i+(2+3\lambda)\hat j+(6\lambda-4)\hat k$