NEET/JEE Coaching Scholarship
Get up to 90% Scholarship on Offline NEET/JEE coaching from top Institutes
Search Colleges, Exams, Schools & more
NCERT Solutions for Class 12 Maths Chapter 13 - Probability
Edited By Komal Miglani | Updated on May 12, 2025 03:09 PM IST | #CBSE Class 12th
Probability is not a certainty, but it is the possibility with a heartbeat. In general terms, probability is how likely something is to happen. It is like a number between 0 and 1. If it is 0, it will not happen, but if it is 1, it will definitely happen. Anything in between 0 and 1 means it might happen. In the Probability Class 12 NCERT solutions, students will learn concepts of probability distributions, random variables, Bayes' theorem, and conditional probability thoroughly. The main goal of these solutions by NCERT is to prepare students for the Class 12 board exam as well as other competitive exams.
This Story also Contains
- NCERT Solution for Class 12 Maths Chapter 13 Solutions: Download PDF
- Important Formulae
- NCERT Solutions for Class 12 Maths Chapter 13: Exercise Questions
- Class 12 Maths NCERT Chapter 13: Extra Question
- Approach to Solve Questions of Probability Class 12
- What Extra Should Students Study Beyond NCERT for JEE?
- NCERT Solutions for Class 12 Maths: Chapter Wise
LiveCBSE Result 2025 (LIVE): Class 10, 12 marksheet likely today at cbse.gov.in, Digilocker; websites to checkMay 12, 2025 | 10:32 PM ISTRead More
No, the Central Board of Secondary Education is yet to declare CBSE Class 10 results 2025. Once declared, the CBSE 10th result link 2025 will be available on the official website, results.cbse.nic.in.
Every day before leaving our houses, we check for weather forecasts. Ever wondered how metrologists predict the weather? Ever thought about how these clothing brands determine what’s going to trend or on what models, and how AI and machine learning work? The solution is in the Probability chapter! Experienced Careers360 teachers abiding by the latest CBSE syllabus have curated these class 12 Maths NCERT solutions of Probability. Students can additionally refer to the NCERT Exemplar Solutions for Class 12 Maths Chapter 13 Probability for better practice and understanding of the topic.
NCERT Solution for Class 12 Maths Chapter 13 Solutions: Download PDF
Students who wish to access the Class 12 Maths Chapter 13 NCERT Solutions can click on the link below to download the complete solution in PDF.
Important Formulae
Conditional Probability: Conditional probability is the likelihood of an event occurring based on the occurrence of a preceding event. For two events A and B with the same sample space, the conditional probability of event A given that B has occurred (P(A|B)) is defined as:
P ( A ∣ B ) = P ( A ∩ B ) P ( B ) (when P(B) ≠ 0)
Other conditional probability relationships:
P ( S ∣ F ) = P ( F ∣ F ) = 1 P ( ( A ∪ B ) ∣ F ) = P ( A ∣ F ) + P ( B ∣ F ) − P ( ( A ∩ B ) ∣ F ) P ( E ′ ∣ F ) = 1 − P ( E ∣ F )
Multiplication Rule: The multiplication rule relates the probability of two events E and F in a sample space S:
P ( E ∩ F ) = P ( E ) ⋅ P ( F ∣ E ) = P ( F ) ⋅ P ( E ∣ F ) (when P(E) ≠ 0 and P(F) ≠ 0)
Independent Events: Two experiments are considered independent if the probability of the events E and F occurring simultaneously is the product of their individual probabilities:
P ( E ∩ F ) = P ( E ) ⋅ P ( F )
Bayes’ Theorem: Bayes’ theorem deals with events E1, E2, …, En that form a partition of the sample space S. It allows the calculation of the probability of event Ei given event A:
P ( E i ∣ A ) = P ( E i ) ⋅ P ( A ∣ E i ) ∑ j = 1 n P ( E j ) ⋅ P ( A ∣ E j ) , for i = 1, 2, …, n
Theorem of Total Probability: Given a partition E1, E2, …, En of the sample space and an event A, the theorem of total probability states:
P ( A ) = P ( E 1 ) ⋅ P ( A ∣ E 1 ) + P ( E 2 ) ⋅ P ( A ∣ E 2 ) + ⋯ + P ( E n ) ⋅ P ( A ∣ E n )
Free download NCERT Class 12 Maths Chapter 13 Question Answer Probability for CBSE Exam.
NCERT Solutions for Class 12 Maths Chapter 13: Exercise Questions
| Class 12 Maths chapter 13 solutions - Exercise: 13.1 Page number: 413-415 Total questions: 17 |
Question 1: Given that E and F are events such that P(E)=0.6,P(F)=0.3 and p(E∩F)=0.2, find P(E∣F) and P(F∣E)
Answer:
It is given that P ( E ) = 0.6 , P ( F ) = 0.3 and p ( E ∩ F ) = 0.2 ,
P ( E | F ) = p ( E ∩ F ) P ( F ) = 0.2 0.3 = 2 3
P ( F | E ) = p ( E ∩ F ) P ( E ) = 0.2 0.6 = 1 3
Question 2: Compute P(A∣B), if P(B)=0.5 and P(A∩B)=0.32
Answer:
It is given that P ( B ) = 0.5 and P ( A ∩ B ) = 0.32
P ( A | B ) = p ( A ∩ B ) P ( B ) = 0.32 0.5 = 0.64
Question 3: If P(A)=0.8,P(B)=0.5 and P(B∣A)=0.4, find
(i) P ( A ∩ B )
(ii) P ( A ∣ B )
(iii) P ( A ∪ B )
Answer:
(i) It is given that P(A)=0.8, P(B)=0.5 and P(B|A)=0.4
P ( B | A ) = p ( A ∩ B ) P ( A )
⇒ 0.4 = p ( A ∩ B ) 0.8
⇒ p ( A ∩ B ) = 0.4 × 0.8
⇒ p ( A ∩ B ) = 0.32
(ii) It is given that P ( A ) = 0.8 , P ( B ) = 0.5 and P ( B ∣ A ) = 0.4 ,
P ( A ∩ B ) = 0.32
P ( A | B ) = p ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 0.32 0.5
⇒ P ( A | B ) = 32 50 = 0.64
(iii) It is given that P ( A ) = 0.8 , P ( B ) = 0.5
P ( A ∩ B ) = 0.32
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
⇒ P ( A ∪ B ) = 0.8 + 0.5 − 0.32
⇒ P ( A ∪ B ) = 1.3 − 0.32
⇒ P ( A ∪ B ) = 0.98
Question 4: Evaluate P(A∪B), if 2P(A)=P(B)=513 and P(A∣B)=25
Answer:
Given in the question 2 P ( A ) = P ( B ) = 5 13 and P ( A ∣ B ) = 2 5
We know that:
P ( A | B ) = p ( A ∩ B ) P ( B )
⇒ 2 5 = p ( A ∩ B ) 5 13
⇒ 2 × 5 5 × 13 = p ( A ∩ B )
⇒ p ( A ∩ B ) = 2 13
Use, p ( A ∪ B ) = p ( A ) + p ( B ) − p ( A ∩ B )
⇒ p ( A ∪ B ) = 5 26 + 5 13 − 2 13
⇒ p ( A ∪ B ) = 11 26
Question 5: If P(A)=611,P(B)=511 and P(A∪B)=711. , find
(i) P ( A ∩ B )
(ii) P ( A ∣ B )
(iii) P ( B ∣ A )
Answer:
(i) Given in the question
P ( A ) = 6 11 , P ( B ) = 5 11 and P ( A ∪ B ) = 7 11 .
By using formula:
p ( A ∪ B ) = p ( A ) + p ( B ) − p ( A ∩ B )
⇒ 7 11 = 6 11 + 5 11 − p ( A ∩ B )
⇒ p ( A ∩ B ) = 11 11 − 7 11
⇒ p ( A ∩ B ) = 4 11
(ii) It is given that - P ( A ) = 6 11 , P ( B ) = 5 11
p ( A ∩ B ) = 4 11
We know that:
P ( A | B ) = p ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 4 11 5 11
⇒ P ( A | B ) = 4 5
(iii) Given in the question-
P ( A ) = 6 11 , P ( B ) = 5 11 and p ( A ∩ B ) = 4 11
Use formula
P ( B | A ) = p ( A ∩ B ) P ( A )
⇒ P ( B | A ) = 4 11 6 11
⇒ P ( B | A ) = 4 6 = 2 3
Question 6: A coin is tossed three times, where
(i) E: head on third toss, F: heads on first two tosses
(ii) E: at least two heads ,F: at most two heads
(iii) E: at most two tails, F: at least one tail
Answer:
(i) The sample space S when a coin is tossed three times is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
It can be seen that the sample space (S) has 8 elements.
Total number of outcomes = 2 3 = 8
According to question
E: head on third toss, F: heads on first two tosses
E = { H H H , T T H , H T H , T H H }
F = { H H H , H H T }
E ∩ F = H H H
P ( F ) = 2 8 = 1 4
P ( E ∩ F ) = 1 8
P ( E | F ) = P ( E ∩ F ) P ( F )
⇒ P ( E | F ) = 1 8 1 4
⇒ P ( E | F ) = 4 8 = 1 2
(ii) The sample space S when a coin is tossed three times is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
It can be seen that the sample space (S) has 8 elements.
Total number of outcomes = 2 3 = 8
According to question
E : at least two heads , F : at most two heads
E = { H H H , H T H , T H H , H H T } = 4
F = { H T H , H H T , T H H , T T T , H T T , T T H , T H T } = 7
E ∩ F = { H T H , T H H , H H T } = 3
P ( F ) = 7 8
P ( E ∩ F ) = 3 8
⇒ P ( E | F ) = P ( E ∩ F ) P ( F )
⇒ P ( E | F ) = 3 8 7 8
P ( E | F ) = 3 7
(iii) The sample space S when a coin is tossed three times is
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
It can be seen that the sample space (S) has 8 elements.
Total number of outcomes = 2 3 = 8
According to the question,
E: at most two tails, F: at least one tail
E = { H H H , T T H , H T H , T H H , T H T , H T T , H H T } = 7
F = { T T T , T T H , H T H , T H H , T H T , H T T , H H T } = 7
E ∩ F = { T T H , H T H , T H H , T H T , H T T , H H T } = 6
P ( F ) = 7 8
P ( E ∩ F ) = 6 8 = 3 4
P ( E | F ) = P ( E ∩ F ) P ( F )
⇒ P ( E | F ) = 3 4 7 8
⇒ P ( E | F ) = 6 7
Question 7: Two coins are tossed once, where
(i) E : tail appears on one coin, F : one coin shows head
(ii) E : no tail appears,F : no head appears
Answer:
(i) E : tail appears on one coin, F : one coin shows head
Total outcomes =4
E = { H T , T H } = 2
F = { H T , T H } = 2
E ∩ F = { H T , T H } = 2
P ( F ) = 2 4 = 1 2
P ( E ∩ F ) = 2 4 = 1 2
P ( E | F ) = P ( E ∩ F ) P ( F )
⇒ P ( E | F ) = 1 2 1 2
⇒ P ( E | F ) = 1
(ii) E : no tail appears, F : no head appears
Total outcomes =4
E = H H F = T T
E ∩ F = ϕ
n ( E ∩ F ) = 0
P ( F ) = 1
P ( E ∩ F ) = 0 4 = 0
P ( E | F ) = P ( E ∩ F ) P ( F )
P ( E | F ) = 0 1 = 0
Question 8: A die is thrown three times,
E : 4 appears on the third toss, F : 6 and 5 appears respectively on first two tosses
Answer:
E: 4 appears on the third toss, F: 6 and 5 appear respectively on the first two tosses
Total outcomes = 6 3 = 216
n ( E ) = 36 as 4 is fixed at third place.
F = { 651 , 652 , 653 , 654 , 655 , 656 }
n ( F ) = 6
E ∩ F = { 654 }
n ( E ∩ F ) = 1
P ( E ∩ F ) = 1 216
P ( F ) = 6 216 = 1 36
P ( E | F ) = P ( E ∩ F ) P ( F )
⇒ P ( E | F ) = 1 216 1 36
⇒ P ( E | F ) = 1 6
Question 9: Mother, father and son line up at random for a family picture
E : son on one end, F : father in middle
Answer:
E: son on one end, F: father in middle
Total outcomes = 3 ! = 3 × 2 = 6
Let S be son, M be mother and F be father.
Then we have,
E = { S M F , S F M , F M S , M F S }
n ( E ) = 4
F = { S F M , M F S }
n ( F ) = 2
E ∩ F = { S F M , M F S }
n ( E ∩ F ) = 2
P ( F ) = 2 6 = 1 3
P ( E ∩ F ) = 2 6 = 1 3
P ( E | F ) = P ( E ∩ F ) P ( F )
⇒ P ( E | F ) = 1 3 1 3
⇒ P ( E | F ) = 1
Question 10: A black and a red dice are rolled.
Answer:
(i) A black and a red dice are rolled.
Total outcomes = 6 2 = 36
Let the A be an event obtaining a sum greater than 9 and B be an event that the black die resulted in a 5.
A = { 46 , 55 , 56 , 64 , 65 , 66 }
n ( A ) = 6
B = { 51 , 52 , 53 , 54 , 55 , 56 }
n ( B ) = 6
A ∩ B = { 55 , 56 }
n ( A ∩ B ) = 2
P ( A ∩ B ) = 2 36
P ( B ) = 6 36
P ( A | B ) = P ( A ∩ B ) P ( B )
P ( A | B ) = 2 36 6 36 = 2 6 = 1 3
(ii) A black and a red dice are rolled.
Total outcomes = 6 2 = 36
Let the A be event obtaining a sum 8 and B be a event thatthat the red die resulted in a number less than 4 .
A = { 26 , 35 , 53 , 44 , 62 , }
n ( A ) = 5
Red dice is rolled after black dice.
B = { 11 , 12 , 13 , 21 , 22 , 23 , 31 , 32 , 33 , 41 , 42 , 43 , 51 , 52 , 53 , 61 , 62 , 63 }
n ( B ) = 18
A ∩ B = { 53 , 62 }
n ( A ∩ B ) = 2
P ( A ∩ B ) = 2 36
P ( B ) = 18 36
P ( A | B ) = P ( A ∩ B ) P ( B )
P ( A | B ) = 2 36 18 36 = 2 18 = 1 9
Question 11: A fair die is rolled. Consider events E={1,3,5},F{2,3} and G={2,3,4,5} Find
(i) P ( E ∣ F ) and P ( F ∣ E )
(ii) P ( E ∣ G ) and P ( G ∣ E )
(iii) P ( ( E ∪ F ) ∣ G ) and P ( ( E ∩ F ) ∣ G )
Answer:
(i) A fair die is rolled.
Total oucomes = { 1 , 2 , 3 , 4 , 5 , 6 } = 6
E = { 1 , 3 , 5 } , F { 2 , 3 }
E ∩ F = { 3 }
n ( E ∩ F ) = 1
n ( F ) = 2
n ( E ) = 3
P ( E ) = 3 6 P ( F ) = 2 6 and P ( E ∩ F ) = 1 6
P ( E | F ) = P ( E ∩ F ) P ( F )
⇒ P ( E | F ) = 1 6 2 6
⇒ P ( E | F ) = 1 2
P ( F | E ) = P ( F ∩ E ) P ( E )
⇒ P ( F | E ) = 1 6 3 6
⇒ P ( F | E ) = 1 3
(ii) A fair die is rolled.
Total oucomes = { 1 , 2 , 3 , 4 , 5 , 6 } = 6
E = { 1 , 3 , 5 } , G = { 2 , 3 , 4 , 5 }
E ∩ G = { 3 , 5 }
n ( E ∩ G ) = 2
n ( G ) = 4
n ( E ) = 3
P ( E ) = 3 6 P ( G ) = 4 6 P ( E ∩ F ) = 2 6
P ( E | G ) = P ( E ∩ G ) P ( G )
⇒ P ( E | G ) = 2 6 4 6
⇒ P ( E | G ) = 2 4 = 1 2
P ( G | E ) = P ( G ∩ E ) P ( E )
⇒ P ( G | E ) = 2 6 3 6
⇒ P ( G | E ) = 2 3
(iii) A fair die is rolled.
Total oucomes = { 1 , 2 , 3 , 4 , 5 , 6 } = 6
E = { 1 , 3 , 5 } , F { 2 , 3 } and G = { 2 , 3 , 4 , 5 }
E ∩ G = { 3 , 5 } , F ∩ G = { 2 , 3 }
( E ∩ G ) ∩ G = { 3 }
P [ ( E ∩ G ) ∩ G ] = 1 6 P ( E ∩ G ) = 2 6 P ( F ∩ G ) = 2 6
P ( ( E ∪ F ) | G ) = P ( E | G ) + P ( F | G ) − P [ ( E ∩ F ) | G ]
⇒ = P ( E ∩ G ) P ( G ) + P ( F ∩ G ) P ( G ) − P ( ( E ∩ F ) ∩ G ) P ( G )
⇒ = 2 6 4 6 + 2 6 4 6 − 1 6 4 6
⇒ = 2 4 + 2 4 − 1 4
⇒ = 3 4
P ( ( E ∩ F ) | G ) = P ( ( E ∩ F ) ∩ G ) P ( G )
⇒ P ( ( E ∩ F ) | G ) = 1 6 4 6
⇒ P ( ( E ∩ F ) | G ) = 1 4
Answer:
(i) Assume that each born child is equally likely to be a boy or a girl.
Let first and second girl are denoted by G 1 a n d G 2 respectively also first and second boy are denoted by B 1 a n d B 2
If a family has two children, then total outcomes = 2 2 = 4 = { ( B 1 B 2 ) , ( G 1 G 2 ) , ( G 1 B 2 ) , ( G 2 B 1 ) }
Let A= both are girls = { ( G 1 G 2 ) }
and B= the youngest is a girl = = { ( G 1 G 2 ) , ( B 1 G 2 ) }
A ∩ B = { ( G 1 G 2 ) }
P ( A ∩ B ) = 1 4 P ( B ) = 2 4
P ( A | B ) = P ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 1 4 2 4
⇒ P ( A | B ) = 1 2
Therefore, the required probability is 1/2
(ii) Assume that each born child is equally likely to be a boy or a girl.
Let first and second girl are denoted by G 1 a n d G 2 respectively also first and second boy are denoted by B 1 a n d B 2
If a family has two children, then total outcomes = 2 2 = 4 = { ( B 1 B 2 ) , ( G 1 G 2 ) , ( G 1 B 2 ) , ( G 2 B 1 ) }
Let A= both are girls = { ( G 1 G 2 ) }
and C= at least one is a girl = = { ( G 1 G 2 ) , ( B 1 G 2 ) , ( G 1 B 2 ) }
A ∩ B = { ( G 1 G 2 ) }
P ( A ∩ B ) = 1 4 P ( C ) = 3 4
P ( A | C ) = P ( A ∩ C ) P ( C )
⇒ P ( A | C ) = 1 4 3 4
⇒ P ( A | C ) = 1 3
Answer:
An instructor has a question bank consisting of 300 easy True / False questions, 200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions.
Total number of questions = 300 + 200 + 500 + 400 = 1400
Let A = question be easy.
n ( A ) = 300 + 500 = 800
P ( A ) = 800 1400 = 8 14
Let B = multiple choice question
n ( B ) = 500 + 400 = 900
P ( B ) = 900 1400 = 9 14
A ∩ B = easy multiple questions
n ( A ∩ B ) = 500
P ( A ∩ B ) = 500 1400 = 5 14
P ( A | B ) = P ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 5 14 9 14
⇒ P ( A | B ) = 5 9
Therefore, the required probability is 5/9
Answer:
Two dice are thrown.
Total outcomes = 6 2 = 36
Let A be the event ‘the sum of numbers on the dice is 4.
A = { ( 13 ) , ( 22 ) , ( 31 ) }
Let B be the event that two numbers appearing on throwing two dice are different.
B = { ( 12 ) , ( 13 ) , ( 14 ) , ( 15 ) , ( 16 ) , ( 21 ) ( 23 ) , ( 24 ) , ( 25 ) , ( 26 , ) ( 31 ) , ( 32 ) , ( 34 ) , ( 35 ) , ( 36 ) , ( 41 ) , ( 42 ) , ( 43 ) , ( 45 ) , ( 46 ) , ( 51 ) , ( 52 ) , ( 53 ) , ( 54 ) , ( 56 ) , ( 61 ) , ( 62 ) , ( 63 ) , ( 64 ) , ( 65 ) } n ( B ) = 30
P ( B ) = 30 36
A ∩ B = { ( 13 ) , ( 31 ) }
n ( A ∩ B ) = 2
P ( A ∩ B ) = 2 36
P ( A | B ) = P ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 2 36 30 36
⇒ P ( A | B ) = 2 30 = 1 15
Therefore, the required probability is 1/15
Answer:
Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin.
Total outcomes = { ( 1 H ) , ( 1 T ) , ( 2 H ) , ( 2 T ) , ( 31 ) , ( 32 ) , ( 33 ) , ( 34 ) , ( 35 ) , ( 36 ) , ( 4 H ) , ( 4 T ) , ( 5 H ) , ( 5 T ) , ( 61 ) , ( 62 ) , ( 63 ) , ( 64 ) , ( 65 ) , ( 66 ) }
Total number of outcomes =20
Let A be a event when coin shows a tail.
A = { ( ( 1 T ) , ( 2 T ) , ( 4 T ) , ( 5 T ) }
Let B be a event that ‘at least one die shows a 3’.
B = { ( 31 ) , ( 32 ) , ( 33 ) , ( 34 ) , ( 35 ) , ( 36 ) , ( 63 ) }
n ( B ) = 7
P ( B ) = 7 20
A ∩ B = ϕ
n ( A ∩ B ) = 0
P ( A ∩ B ) = 0 20 = 0
P ( A | B ) = P ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 0 7 20
⇒ P ( A | B ) = 0
Question 16: In the following Exercise 16 choose the correct answer:
If P(A)=12,P(B)=0, then P(A∣B) is
Answer:
It is given that
P ( A ) = 1 2 , P ( B ) = 0 ,
P ( A | B ) = P ( A ∩ B ) P ( B )
⇒ P ( A | B ) = P ( A ∩ B ) 0
Hence, P (A|B) is not defined.
Thus, the correct option is C.
Question 17: In the following Exercise 17 choose the correct answer:
If A and B are events such that P(A∣B)=P(B∣A), then
Answer:
It is given that P ( A ∣ B ) = P ( B ∣ A ) ,
⇒ P ( A ∩ B ) P ( B ) = P ( A ∩ B ) P ( A )
⇒ P ( A ) = P ( B )
Hence, option D is correct.
| Class 12 Maths chapter 13 solutions - Exercise: 13.2 Page number: 421-423 Total questions: 18 |
Question 1: If P(A)=35 and P(B)=15, find P(A∩B) if A and B are independent events.
Answer:
P ( A ) = 3 5 and P ( B ) = 1 5 ,
Given : A and B are independent events.
So we have, P ( A ∩ B ) = P ( A ) . P ( B )
⇒ P ( A ∩ B ) = 3 5 × 1 5
⇒ P ( A ∩ B ) = 3 25
Answer:
Two cards are drawn at random and without replacement from a pack of 52 playing cards.
There are 26 black cards in a pack of 52.
Let P ( A ) be the probability that first cards is black.
Then, we have
P ( A ) = 26 52 = 1 2
Let P ( B ) be the probability that second cards is black.
Then, we have
P ( B ) = 25 51
The probability that both the cards are black = P ( A ) . P ( B )
⇒ = 1 2 × 25 51
⇒ = 25 102
Answer:
Total oranges = 15
Good oranges = 12
Bad oranges = 3
Let P ( A ) be the probability that first orange is good.
The, we have
P ( A ) = 12 15 = 4 5
Let P ( B ) be the probability that second orange is good.
P ( B ) = 11 14
Let P ( C ) be the probability that third orange is good.
P ( C ) = 10 13
The probability that a box will be approved for sale = P ( A ) . P ( B ) . P ( C )
⇒ 4 5 . 11 14 . 10 13
⇒ 44 91
Answer:
A fair coin and an unbiased die are tossed,then total outputs are:
= { ( H 1 ) , ( H 2 ) , ( H 3 ) , ( H 4 ) , ( H 5 ) , ( H 6 ) , ( T 1 ) , ( T 2 ) , ( T 3 ) , ( T 4 ) , ( T 5 ) , ( T 6 ) }
= 12
A is the event ‘head appears on the coin’ .
Total outcomes of A are : = { ( H 1 ) , ( H 2 ) , ( H 3 ) , ( H 4 ) , ( H 5 ) , ( H 6 ) }
P ( A ) = 6 12 = 1 2
B is the event ‘3 on the die’.
Total outcomes of B are : = { ( T 3 ) , ( H 3 ) }
P ( B ) = 2 12 = 1 6
∴ A ∩ B = ( H 3 )
P ( A ∩ B ) = 1 12
Also, P ( A ∩ B ) = P ( A ) . P ( B )
P ( A ∩ B ) = 1 2 × 1 6 = 1 12
Hence, A and B are independent events.
Answer:
Total outcomes = { 1 , 2 , 3 , 4 , 5 , 6 } = 6 .
A is the event, ‘the number is even,’
Outcomes of A = { 2 , 4 , 6 }
n ( A ) = 3.
P ( A ) = 3 6 = 1 2
B is the event, ‘the number is red’.
Outcomes of B = { 1 , 2 , 3 }
n ( B ) = 3.
P ( B ) = 3 6 = 1 2
∴ ( A ∩ B ) = { 2 }
n ( A ∩ B ) = 1
P ( A ∩ B ) = 1 6
Also,
P ( A ∩ B ) = P ( A ) . P ( B )
P ( A ∩ B ) = 1 2 × 1 2 = 1 4 ≠ 1 6
Thus, both the events A and B are not independent.
Question 6: Let E and F be events with P(E)=35,P(F)=310 and P(E∩F)=15. Are E and F independent?
Answer:
Given :
P ( E ) = 3 5 , P ( F ) = 3 10 and P ( E ∩ F ) = 1 5 .
For events E and F to be independent, we need
P ( E ∩ F ) = P ( E ) . P ( F )
P ( E ∩ F ) = 3 5 × 3 10 = 9 50 ≠ 1 5
Hence, E and F are not independent events.
Question 7: Given that the events A and B are such that P(A)=12,P(A∪B)=35 and P(B)=p. Find p if they are
(ii) independent
Answer:
(i) Given,
P ( A ) = 1 2 , P ( A ∪ B ) = 3 5
Also, A and B are mutually exclusive means A ∩ B = ϕ .
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
⇒ 3 5 = 1 2 + P ( B ) − 0
⇒ P ( B ) = 3 5 − 1 2 = 1 10
(ii) Given,
P ( A ) = 1 2 , P ( A ∪ B ) = 3 5
Also, A and B are independent events means
P ( A ∩ B ) = P ( A ) . P ( B ) . Also P ( B ) = p .
P ( A ∩ B ) = P ( A ) . P ( B ) = p 2
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
⇒ 3 5 = 1 2 + p − p 2
⇒ p 2 = 3 5 − 1 2 = 1 10
⇒ p = 2 10 = 1 5
Question 8: Let A and B be independent events with P(A)=0.3 and P(B)=0.4 Find
(i) P ( A ∩ B )
(ii) P ( A ∪ B )
(iii) P ( A ∣ B )
(iv) P ( B ∣ A )
Answer:
(i) P ( A ) = 0.3 and P ( B ) = 0.4
Given : A and B be independent events
So, we have
P ( A ∩ B ) = P ( A ) . P ( B )
⇒ P ( A ∩ B ) = 0.3 × 0.4 = 0.12
(ii) P ( A ) = 0.3 and P ( B ) = 0.4
Given : A and B be independent events
So, we have
P ( A ∩ B ) = P ( A ) . P ( B )
P ( A ∩ B ) = 0.3 × 0.4 = 0.12
We have, P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
⇒ P ( A ∪ B ) = 0.3 + 0.4 − 0.12 = 0.58
(iii) P ( A ) = 0.3 and P ( B ) = 0.4
Given : A and B be independent events
So, we have P ( A ∩ B ) = 0.12
P ( A | B ) = P ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 0.12 0.4 = 0.3
(iv) P ( A ) = 0.3 and P ( B ) = 0.4
Given : A and B be independent events
So, we have P ( A ∩ B ) = 0.12
P ( B | A ) = P ( A ∩ B ) P ( A )
⇒ P ( B | A ) = 0.12 0.3 = 0.4
Question 9: If A and B are two events such that P(A)=14,P(B)=12 and P(A∩B)=18, find P(notAandnotB).
Answer:
If A and B are two events such that P ( A ) = 1 4 , P ( B ) = 1 2 and P ( A ∩ B ) = 1 8 ,
P ( n o t A a n d n o t B ) = P ( A ′ ∩ B ′ )
P ( n o t A a n d n o t B ) = P ( A ∪ B ) ′ use, ( P ( A ′ ∩ B ′ ) = P ( A ∪ B ) ′ )
⇒ 1 − ( P ( A ) + P ( B ) − P ( A ∩ B ) )
⇒ 1 − ( 1 4 + 1 2 − 1 8 )
⇒ 1 − ( 6 8 − 1 8 )
⇒ 1 − 5 8
⇒ 3 8
Question 10: Events A and B are such that P(A)=12,P(B)=712 and P(notAornotB)=14. State whether A and B are independent ?
Answer:
If A and B are two events such that P ( A ) = 1 2 , P ( B ) = 7 12 and P ( n o t A o r n o t B ) = 1 4 .
P ( A ′ ∪ B ′ ) = 1 4
P ( A ∩ B ) ′ = 1 4 ( A ′ ∪ B ′ = ( A ∩ B ) ′ )
⇒ 1 − P ( A ∩ B ) = 1 4
⇒ P ( A ∩ B ) = 1 − 1 4 = 3 4
A l s o P ( A ∩ B ) = P ( A ) . P ( B )
P ( A ∩ B ) = 1 2 × 7 12 = 7 24
As we can see 3 4 ≠ 7 24
Hence, A and B are not independent.
Question 11: Given two independent events A and B such that P(A)=0.3,P(B)=0.6, Find
(i) P ( A a n d B )
(iii) P ( A o r B )
(iv) P ( n e i t h e r A n o r B )
Answer:
(i) P ( A ) = 0.3 , P ( B ) = 0.6 ,
Given two independent events A and B .
P ( A ∩ B ) = P ( A ) . P ( B )
⇒ P ( A ∩ B ) = 0.3 × 0.6 = 0.18
Also , we know P ( A and B ) = P ( A ∩ B ) = 0.18
(ii) P ( A ) = 0.3 , P ( B ) = 0.6 ,
Given two independent events A and B.
P ( A a n d n o t B ) = P ( A ) − P ( A ∩ B )
0.3 − 0.18 = 0.12
(iii) P ( A ) = 0.3 , P ( B ) = 0.6 ,
P ( A ∩ B ) = 0.18
P ( A o r B ) = P ( A ∪ B )
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
⇒ 0.3 + 0.6 − 0.18
⇒ 0.9 − 0.18
⇒ 0.72
(iv) P ( A ) = 0.3 , P ( B ) = 0.6 ,
P ( A ∩ B ) = 0.18
P ( A o r B ) = P ( A ∪ B )
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
⇒ 0.3 + 0.6 − 0.18
⇒ 0.9 − 0.18
⇒ 0.72
P ( n e i t h e r A n o r B ) = P ( A ′ ∩ B ′ )
= P ( ( A ∪ B ) ′ )
= 1 − P ( A ∪ B )
1 − 0.72
0.28
Question 12: A die is tossed thrice. Find the probability of getting an odd number at least once.
Answer:
A die is tossed thrice.
Outcomes = { 1 , 2 , 3 , 4 , 5 , 6 }
Odd numbers = { 1 , 3 , 5 }
The probability of getting an odd number at first throw
= 3 6 = 1 2
The probability of getting an even number
= 3 6 = 1 2
Probability of getting even number three times
= 1 2 × 1 2 × 1 2 = 1 8
The probability of getting an odd number at least once = 1 - the probability of getting an odd number in none of throw
= 1 - probability of getting even number three times
⇒ 1 − 1 8
⇒ 7 8
(ii) first ball is black and second is red.
(iii) one of them is black and other is red.
Answer:
(i) Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls.
Total balls =18
Black balls = 10
Red balls = 8
The probability of getting a red ball in first draw
= 8 18 = 4 9
The ball is repleced after drawing first ball.
The probability of getting a red ball in second draw
= 8 18 = 4 9
the probability that both balls are red
= 4 9 × 4 9 = 16 81
(ii) Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls.
Total balls =18
Black balls = 10
Red balls = 8
The probability of getting a black ball in the first draw
= 10 18 = 5 9
The ball is replaced after drawing the first ball.
The probability of getting a red ball in the second draw
= 8 18 = 4 9
the probability that the first ball is black and the second is red
= 5 9 × 4 9 = 20 81
(iii) Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls.
Total balls =18
Black balls = 10
Red balls = 8
Let the first ball is black and the second ball is red.
The probability of getting a black ball in the first draw
= 10 18 = 5 9
The ball is replaced after drawing the first ball.
The probability of getting a red ball in the second draw
= 8 18 = 4 9
the probability that the first ball is black and the second is red
= 5 9 × 4 9 = 20 81 . . . . . . . . . . . . . . . . . . . . . . . . . . .1
Let the first ball is red and the second ball is black.
The probability of getting a red ball in the first draw
= 8 18 = 4 9
The probability of getting a black ball in the second draw
= 10 18 = 5 9
the probability that the first ball is red and the second is black
= 4 9 × 5 9 = 20 81 . . . . . . . . . . . . . . . . . . . . . . . . . . .2
Thus,
The probability that one of them is black and the other is red = the probability that the first ball is black and the second is red + the probability that the first ball is red and the second is black = 20 81 + 20 81 = 40 81
(ii) exactly one of them solves the problem
Answer:
(i) P ( A ) = 1 2 and P ( B ) = 1 3
Since, problem is solved independently by A and B,
∴ P ( A ∩ B ) = P ( A ) . P ( B )
⇒ P ( A ∩ B ) = 1 2 × 1 3
⇒ P ( A ∩ B ) = 1 6
probability that the problem is solved = P ( A ∪ B )
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
⇒ P ( A ∪ B ) = 1 2 + 1 3 − 1 6
⇒ P ( A ∪ B ) = 5 6 − 1 6
⇒ P ( A ∪ B ) = 4 6 = 2 3
(ii) P ( A ) = 1 2 and P ( B ) = 1 3
P ( A ′ ) = 1 − P ( A ) , P ( B ′ ) = 1 − P ( B )
P ( A ′ ) = 1 − 1 2 = 1 2 , P ( B ′ ) = 1 − 1 3 = 2 3
probability that exactly one of them solves the problem = P ( A ∩ B ′ ) + P ( A ′ ∩ B )
probability that exactly one of them solves the problem = P ( A ) . P ( B ′ ) + P ( A ′ ) P ( B )
⇒ 1 2 × 2 3 + 1 2 × 1 3
⇒ 2 6 + 1 6
⇒ 3 6 = 1 2
(i) E : ‘the card drawn is a spade’
F : ‘the card drawn is an ace’
F : ‘the card drawn is a king’
(iii) E : ‘the card drawn is a king or queen’
F : ‘the card drawn is a queen or jack’.
Answer:
(i) One card is drawn at random from a well shuffled deck of 52 cards
Total ace = 4
total spades =13
E : ‘the card drawn is a spade
F : ‘the card drawn is an ace’
P ( E ) = 13 52 = 1 4
P ( F ) = 4 52 = 1 13
E ∩ F : a card which is spade and ace = 1
P ( E ∩ F ) = 1 52
P ( E ) . P ( F ) = 1 4 × 1 13 = 1 52
⇒ P ( E ∩ F ) = P ( E ) . P ( F ) = 1 52
Hence, E and F are independent events.
(ii) One card is drawn at random from a well shuffled deck of 52 cards
Total black card = 26
total king =4
E : ‘the card drawn is black’
F : ‘the card drawn is a king’
P ( E ) = 26 52 = 1 2
P ( F ) = 4 52 = 1 13
E ∩ F : a card which is black and king = 2
P ( E ∩ F ) = 2 52 = 1 26
P ( E ) . P ( F ) = 1 2 × 1 13 = 1 26
⇒ P ( E ∩ F ) = P ( E ) . P ( F ) = 1 26
Hence, E and F are independent events .
(iii) One card is drawn at random from a well shuffled deck of 52 cards
Total king or queen = 8
total queen or jack = 8
E : ‘the card drawn is a king or queen’
F : ‘the card drawn is a queen or jack’.
P ( E ) = 8 52 = 2 13
P ( F ) = 8 52 = 2 13
E ∩ F : a card which is queen = 4
P ( E ∩ F ) = 4 52 = 1 13
P ( E ) . P ( F ) = 2 13 × 2 13 = 4 169
⇒ P ( E ∩ F ) ≠ P ( E ) . P ( F )
Hence, E and F are not independent events
(a) Find the probability that she reads neither Hindi nor English newspapers
(b) If she reads Hindi newspaper, find the probability that she reads English newspaper.
(c) If she reads English newspaper, find the probability that she reads Hindi newspaper.
Answer:
(a) H : 60 o / o of the students read Hindi newspaper,
E : 40 o / o read English newspaper and
H ∩ E : 20 o / o read both Hindi and English newspapers.
P ( H ) = 60 100 = 6 10 = 3 5
P ( E ) = 40 100 = 4 10 = 2 5
P ( H ∩ E ) = 20 100 = 2 10 = 1 5
the probability that she reads neither Hindi nor English newspapers = 1 − P ( H ∪ E )
= 1 − ( P ( H ) + P ( E ) − P ( H ∩ E ) )
⇒ 1 − ( 3 5 + 2 5 − 1 5 )
⇒ 1 − 4 5
⇒ 1 5
(b) H : 60 o / o of the students read Hindi newspaper,
E : 40 o / o read English newspaper and
H ∩ E : 20 o / o read both Hindi and English newspapers.
P ( H ) = 60 100 = 6 10 = 3 5
P ( E ) = 40 100 = 4 10 = 2 5
P ( H ∩ E ) = 20 100 = 2 10 = 1 5
The probability that she reads English newspaper if she reads Hindi newspaper = P ( E | H )
P ( E | H ) = P ( E ∩ H ) P ( H )
P ( E | H ) = 1 5 3 5
P ( E | H ) = 1 3
(c) H : 60 o / o of the students read Hindi newspaper,
E : 40 o / o read English newspaper and
H ∩ E : 20 o / o read both Hindi and English newspapers.
P ( H ) = 60 100 = 6 10 = 3 5
P ( E ) = 40 100 = 4 10 = 2 5
P ( H ∩ E ) = 20 100 = 2 10 = 1 5
the probability that she reads Hindi newspaper if she reads English newspaper = P ( H | E )
P ( H | E ) = P ( H ∩ E ) P ( E )
P ( H | E ) = 1 5 2 5
P ( H | E ) = 1 2
Question 17: The probability of obtaining an even prime number on each die, when a pair of dice is rolled is
Answer:
when a pair of dice is rolled, total outcomes = 6 2 = 36
Even prime number = { 2 }
n ( e v e n p r i m e n u m b e r ) = 1
The probability of obtaining an even prime number on each die = P ( E )
P ( E ) = 1 36
Option D is correct.
Question 18: Two events A and B will be independent, if
(A) A and B are mutually exclusive
Answer:
Two events A and B will be independent if
P ( A ∩ B ) = P ( A ) . P ( B )
Or P ( A ′ ∩ B ′ ) = P ( A ′ B ′ ) = P ( A ′ ) . P ( B ′ ) = ( 1 − P ( A ) ) . ( 1 − P ( B ) )
Option B is correct.
| Class 12 Maths chapter 13 solutions - Exercise: 13.3 Page number: 431-433 Total questions: 14 |
Answer:
Black balls = 5
Red balls = 5
Total balls = 10
CASE 1 Let red ball be drawn in first attempt.
P ( d r a w i n g r e d b a l l ) = 5 10 = 1 2
Now two red balls are added in urn .
Now red balls = 7, black balls = 5
Total balls = 12
P ( d r a w i n g r e d b a l l ) = 7 12
CASE 2
Let black ball be drawn in first attempt.
P ( d r a w i n g b l a c k b a l l ) = 5 10 = 1 2
Now two black balls are added in urn .
Now red balls = 5, black balls = 7
Total balls = 12
P ( d r a w i n g r e d b a l l ) = 5 12
the probability that the second ball is red =
⇒ 1 2 × 7 12 + 1 2 × 5 12
⇒ 7 24 + 5 24
⇒ 12 24 = 1 2
Answer:
BAG 1 : Red balls =4 Black balls=4 Total balls = 8
BAG 2 : Red balls = 2 Black balls = 6 Total balls = 8
B1 : selecting bag 1
B2 : selecting bag 2
P ( B 1 ) = P ( B 2 ) = 1 2
Let R be a event of getting red ball
P ( R | B 1 ) = P ( d r a w i n g r e d b a l l f r o m f i r s t b a g ) = 4 8 = 1 2
P ( R | B 2 ) = P ( d r a w i n g r e d b a l l f r o m s e c o n d b a g ) = 2 8 = 1 4
probability that the ball is drawn from the first bag,
given that it is red is P ( B 1 | R ) .
Using Bayes' theorem, we have
P ( B 1 | R ) = P ( B 1 ) . P ( R | B 1 ) P ( B 1 ) . P ( R | B 1 ) + P ( B 2 ) . P ( R | B 2 )
⇒ P ( B 1 | R ) = 1 2 × 1 2 1 2 × 1 2 + 1 2 × 1 4
⇒ P ( B 1 | R ) = 1 4 1 4 + 1 8
⇒ P ( B 1 | R ) = 1 4 3 8
⇒ P ( B 1 | R ) = 2 3
Answer:
H : reside in hostel
D : day scholars
A : students who attain grade A
P ( H ) = 60 100 = 6 10 = 3 5
P ( D ) = 40 100 = 4 10 = 2 5
P ( A | H ) = 30 100 = 3 10
P ( A | D ) = 20 100 = 2 10 = 1 5
By Bayes' theorem :
P ( H | A ) = P ( H ) . P ( A | H ) P ( H ) . P ( A | H ) + P ( D ) . P ( A | D )
⇒ P ( H | A ) = 3 5 × 3 10 3 5 × 3 10 + 2 5 × 1 5
⇒ P ( H | A ) = 9 50 9 50 + 2 25
⇒ P ( H | A ) = 9 50 13 50
⇒ P ( H | A ) = 9 13
Answer:
A : Student knows answer.
B : Student guess the answer
C : Answer is correct
P ( A ) = 3 4 P ( B ) = 1 4
P ( C | A ) = 1
P ( C | B ) = 1 4
By Bayes' theorem :
P ( A | C ) = P ( A ) . P ( C | A ) P ( A ) . P ( C | A ) + P ( B ) . P ( C | B )
⇒ P ( A | C ) = 3 4 × 1 3 4 × 1 + 1 4 × 1 4
⇒ 3 4 3 4 + 1 16 = 3 4 13 16
⇒ P ( A | C ) = 12 13
Answer:
A : Person selected is having the disease
B : Person selected is not having the disease.
C :Blood result is positive.
P ( A ) = 0.1 % = 1 1000 = 0.001
P ( B ) = 1 − P ( A ) = 1 − 0.001 = 0.999
P ( C | A ) = 99 % = 0.99
P ( C | B ) = 0.5 % = 0.005
By Bayes' theorem :
P ( A | C ) = P ( A ) . P ( C | A ) P ( A ) . P ( C | A ) + P ( B ) . P ( C | B )
⇒ 0.001 × 0.99 0.001 × 0.99 + 0.999 × 0.005
⇒ 0.00099 0.00099 + 0.004995
⇒ 0.00099 0.005985 = 990 5985
⇒ 22 133
Answer:
Given : A : chossing a two headed coin
B : chossing a biased coin
C : chossing a unbiased coin
P ( A ) = P ( B ) = P ( C ) = 1 3
D : event that coin tossed show head.
P ( D | A ) = 1
Biased coin that comes up heads 75 o / o of the time.
P ( D | B ) = 75 100 = 3 4
P ( D | C ) = 1 2
P ( B | D ) = P ( B ) . P ( D | B ) P ( B ) . P ( D | B ) + P ( A ) . P ( D | A ) + P ( C ) . P ( D | C )
⇒ P ( B | D ) = 1 3 × 1 1 3 × 1 + 1 3 × 3 4 + 1 3 × 1 2
⇒ P ( B | D ) = 1 3 1 3 + 1 4 + 1 6
⇒ P ( B | D ) = 1 3 9 12
⇒ P ( B | D ) = 1 × 12 3 × 9
⇒ P ( B | D ) = 4 9
Answer:
Let A : scooter drivers = 2000
B : car drivers = 4000
C : truck drivers = 6000
Total drivers = 12000
P ( A ) = 2000 12000 = 1 6 = 0.16
P ( B ) = 4000 12000 = 1 3 = 0.33
P ( C ) = 6000 12000 = 1 2 = 0.5
D : the event that person meets with an accident.
P ( D | A ) = 0.01
P ( D | B ) = 0.03
P ( D | C ) = 0.15
P ( A | D ) = P ( A ) . P ( D | A ) P ( B ) . P ( D | B ) + P ( A ) . P ( D | A ) + P ( C ) . P ( D | C )
⇒ P ( A | D ) = 0.16 × 0.01 0.16 × 0.01 + 0.33 × 0.03 + 0.5 × 0.15
⇒ P ( A | D ) = 0.0016 0.0016 + 0.0099 + 0.075
⇒ P ( A | D ) = 0.0016 0.0865
⇒ P ( A | D ) = 0.019
Answer:
A : Items produced by machine A = 60 %
B : Items produced by machine B = 40 %
P ( A ) = 60 100 = 3 5
P ( B ) = 40 100 = 2 5
X : Produced item found to be defective.
P ( X | A ) = 2 100 = 1 50
P ( X | B ) = 1 100
P ( B | X ) = P ( B ) . P ( X | B ) P ( B ) . P ( X | B ) + P ( A ) . P ( X | A )
⇒ P ( B | X ) = 2 5 × 1 100 2 5 × 1 100 + 3 5 × 1 50
⇒ P ( B | X ) = 1 250 1 250 + 3 250
⇒ P ( B | X ) = 1 250 4 250
⇒ P ( B | X ) = 1 4
Hence, the probability that defective item was produced by machine B =
P ( B | X ) = 1 4 .
Answer:
A: the first groups will win
B: the second groups will win
P ( A ) = 0.6
P ( B ) = 0.4
X: Event of introducing a new product.
Probability of introducing a new product if the first group wins : P ( X | A ) = 0.7
Probability of introducing a new product if the second group wins : P ( X | B ) = 0.3
P ( B | X ) = P ( B ) . P ( X | B ) P ( B ) . P ( X | B ) + P ( A ) . P ( X | A )
⇒ p ( B | X ) = 0.4 × 0.3 0.4 × 0.3 + 0.6 × 0.7
⇒ p ( B | X ) = 0.12 0.12 + 0.42
⇒ p ( B | X ) = 0.12 0.54
⇒ p ( B | X ) = 12 54
⇒ p ( B | X ) = 2 9
Hence, the probability that the new product introduced was by the second group :
p ( B | X ) = 2 9
Answer:
Let, A: Outcome on die is 5 or 6.
B: Outcome on die is 1,2,3,4
P ( A ) = 2 6 = 1 3
P ( B ) = 4 6 = 2 3
X: Event of getting exactly one head.
Probability of getting exactly one head when she tosses a coin three times : P ( X | A ) = 3 8
Probability of getting exactly one head when she tosses a coin one time : P ( X | B ) = 1 2
P ( B | X ) = P ( B ) . P ( X | B ) P ( B ) . P ( X | B ) + P ( A ) . P ( X | A )
⇒ P ( B | X ) = 2 3 × 1 2 2 3 × 1 2 + 1 3 × 3 8
⇒ P ( B | X ) = 1 3 1 3 + 1 8
⇒ P ( B | X ) = 1 3 11 24
⇒ P ( B | X ) = 1 × 24 3 × 11 = 8 11
Hence, the probability that she threw 1 , 2 , 3 or 4 with the die =
P ( B | X ) = 8 11
Answer:
Let A: time consumed by machine A = 50 %
B: time consumed by machine B = 30 %
C: time consumed by machine C = 20 %
Total drivers = 12000
P ( A ) = 50 100 = 1 2
P ( B ) = 30 100 = 3 10
P ( C ) = 20 100 = 1 5
D: Event of producing defective items
P ( D | A ) = 1 100
P ( D | B ) = 5 100
P ( D | C ) = 7 100
P ( A | D ) = P ( A ) . P ( D | A ) P ( B ) . P ( D | B ) + P ( A ) . P ( D | A ) + P ( C ) . P ( D | C )
⇒ P ( A | D ) = 1 2 × 1 100 1 2 × 1 100 + 3 10 × 5 100 + 1 5 × 7 100
⇒ P ( A | D ) = 1 2 × 1 100 1 100 ( 1 2 + 3 2 + 7 5 )
⇒ P ( A | D ) = 1 2 ( 17 5 )
⇒ P ( A | D ) = 5 34
Hence, the probability that defective item was produced by A =
P ( A | D ) = 5 34
Answer:
Let A : Event of choosing a diamond card.
B : Event of not choosing a diamond card.
P ( A ) = 13 52 = 1 4
P ( B ) = 39 52 = 3 4
X : The lost card.
If lost card is diamond then 12 diamond cards are left out of 51 cards.
Two diamond cards are drawn out of 12 diamond cards in 12 C 2 ways.
Similarly, two cards are drawn out of 51 cards in 51 C 2 ways.
Probability of getting two diamond cards when one diamond is lost : P ( X | A ) = 12 C 2 51 C 2
P ( X | A ) = 12 ! 10 ! × 2 ! × 49 ! × 2 ! 51 !
⇒ P ( X | A ) = 11 × 12 50 × 51
⇒ P ( X | A ) = 22 425
If lost card is not diamond then 13 diamond cards are left out of 51 cards.
Two diamond cards are drawn out of 13 diamond cards in 13 C 2 ways.
Similarly, two cards are drawn out of 51 cards in 51 C 2 ways.
Probability of getting two diamond cards when one diamond is not lost : P ( X | B ) = 13 C 2 51 C 2
⇒ P ( X | B ) = 13 ! 11 ! × 2 ! × 49 ! × 2 ! 51 !
⇒ P ( X | B ) = 13 × 12 50 × 51
⇒ P ( X | B ) = 26 425
The probability of the lost card being a diamond : P ( B | X )
P ( B | X ) = P ( B ) . P ( X | B ) P ( B ) . P ( X | B ) + P ( A ) . P ( X | A )
⇒ P ( B | X ) = 1 4 × 22 425 1 4 × 22 425 + 3 4 × 26 425
⇒ P ( B | X ) = 11 2 25
⇒ P ( B | X ) = 11 50
Hence, the probability of the lost card being a diamond :
P ( B | X ) = 11 50
Answer:
Let A : A speaks truth
B : A speaks false
P ( A ) = 4 5
P ( B ) = 1 − 4 5 = 1 5
X : Event that head appears.
A coin is tossed , outcomes are head or tail.
Probability of getting head whether A speaks thruth or not is 1 2
P ( X | A ) = P ( X | B ) = 1 2
P ( A | X ) = P ( A ) . P ( X | A ) P ( B ) . P ( X | B ) + P ( A ) . P ( X | A )
⇒ P ( A | X ) = 4 5 × 1 2 4 5 × 1 2 + 1 5 × 1 2
⇒ P ( A | X ) = 4 5 4 5 + 1 5
⇒ P ( A | X ) = 4 5 1 1
⇒ P ( A | X ) = 4 5
The probability that actually there was head is P ( A | X ) = 4 5
Hence, option A is correct.
Question 14: If A and B are two events such that A⊂B and P(B)≠0, then which of the following is correct?
Answer:
If A ⊂ B and P ( B ) ≠ 0 , then
⇒ ( A ∩ B ) = A
Also, P ( A ) < P ( B )
P ( A | B ) = P ( A ∩ B ) P ( B ) = P ( A ) P ( B )
We know that P ( B ) ≤ 1
⇒ 1 ≤ 1 P ( B )
⇒ P ( A ) ≤ P ( A ) P ( B )
⇒ P ( A ) ≤ P ( A | B )
Hence, we can see option C is correct.
| Class 12 Maths chapter 13 solutions - Miscellaneous Exercise Page number: 435-437 Total questions: 13 |
Question 1: A and B are two events such that P(A)≠0. Find P(B∣A), if
(ii) A ∩ B = ϕ
Answer:
(i) A and B are two events such that P ( A ) ≠ 0.
A ⊂ B
⇒ A ∩ B = A
P ( A ∩ B ) = P ( B ∩ A ) = P ( A )
P ( B | A ) = P ( B ∩ A ) P ( A )
⇒ P ( B | A ) = P ( A ) P ( A )
⇒ P ( B | A ) = 1
(ii) A and B are two events such that P ( A ) ≠ 0.
P ( A ∩ B ) = P ( B ∩ A ) = 0
P ( B | A ) = P ( B ∩ A ) P ( A )
⇒ P ( B | A ) = 0 P ( A )
⇒ P ( B | A ) = 0
Question 2: A couple has two children,
Answer:
(i) A couple has two children,
sample space = { ( b , b ) , ( g , g ) , ( b , g ) , ( g , b ) }
Let A be both children are males and B is at least one of the children is male.
( A ∩ B ) = { ( b , b ) }
P ( A ∩ B ) = 1 4
P ( A ) = 1 4
P ( B ) = 3 4
P ( A | B ) = P ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 1 4 3 4 = 1 3
(ii) A couple has two children,
sample space = { ( b , b ) , ( g , g ) , ( b , g ) , ( g , b ) }
Let A be both children are females and B be the elder child is a female.
( A ∩ B ) = { ( g , g ) }
P ( A ∩ B ) = 1 4
P ( A ) = 1 4
P ( B ) = 2 4
P ( A | B ) = P ( A ∩ B ) P ( B )
⇒ P ( A | B ) = 1 4 2 4 = 1 2
Answer:
We have 5 o / o of men and 0.25 o / o of women have grey hair.
Percentage of people with grey hairs = ( 5 + 0.25 ) % = 5.25 %
The probability that the selected haired person is male :
= 5 5.25 = 20 21
Answer:
90 o / o of people are right-handed.
P ( r i g h t − h a n d e d ) = 9 10
P ( l e f t − h a n d e d ) = q = 1 − 9 10 = 1 10
at most 6 of a random sample of 10 people are right-handed.
the probability that more than 6 of a random sample of 10 people are right-handed is given by,
9 10 r . ( 1 10 ) 10 − r
the probability that at most 6 of a random sample of 10 people are right-handed is given by
. 9 10 r . ( 1 10 ) 10 − r
Question 5: If a leap year is selected at random, what is the chance that it will contain 53 tuesdays?
Answer:
In a leap year, there are 366 days.
In 52 weeks, there are 52 Tuesdays.
The probability that a leap year will have 53 Tuesday is equal to the probability that the remaining 2 days are Tuesday.
The remaining 2 days can be :
1. Monday and Tuesday
2. Tuesday and Wednesday
3. Wednesday and Thursday
4. Thursday and Friday
5.friday and Saturday
6.saturday and Sunday
7.sunday and Monday
Total cases = 7.
Favorable cases = 2
Probability of having 53 Tuesday in a leap year = P.
P = 2 7
Question 6: Suppose we have four boxes A,B,C and D containing coloured marbles as given below:
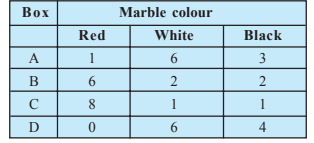
(i) from box A?
(ii) from box B?
(iii) from box C?
Answer:
'
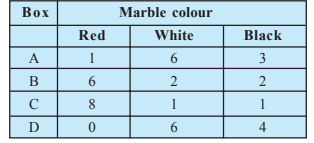(i) Let R be the event of drawing red marble.
Let E A , E B , E C respectively denote the event of selecting box A, B, C.
Total marbles = 40
Red marbles =15
P ( R ) = 15 40 = 3 8
Probability of drawing red marble from box A is P ( E A | R )
P ( E A | R ) = P ( E A ∩ R ) P ( R )
= 1 40 3 8
= 1 15
(ii) Let R be event of drawing red marble.
Let E A , E B , E C respectivly denote event of selecting box A,B,C.
Total marbles = 40
Red marbles =15
P ( R ) = 15 40 = 3 8
Probability of drawing red marble from box B is P ( E B | R )
P ( E B | R ) = P ( E B ∩ R ) P ( R )
= 6 40 3 8
= 2 5
(iii) Let R be event of drawing red marble.
Let E A , E B , E C respectivly denote event of selecting box A,B,C.
Total marbles = 40
Red marbles =15
P ( R ) = 15 40 = 3 8
Probability of drawing red marble from box C is P ( E C | R )
P ( E C | R ) = P ( E C ∩ R ) P ( R )
= 8 40 3 8
= 8 15
Answer:
Let A,E1, E2 respectively denote the event that a person has a heart break, selected person followed the course of yoga and meditation , and the person adopted
the drug prescription.
∴ P ( A ) = 0.40
∴ P ( E 1 ) = P ( E 2 ) = 1 2
P ( A | E 1 ) = 0.40 × 0.70 = 0.28
P ( A | E 2 ) = 0.40 × 0.75 = 0.30
the probability that the patient followed a course of meditation and yoga is P ( E 1 , A )
P ( E 1 , A ) = P ( E 1 ) . P ( E 1 | A ) P ( E 1 ) . P ( E 1 | A ) + P ( E 2 ) . P ( E 2 | A )
P ( E 1 , A ) = 0.5 × 0.28 0.5 × 0.28 + 0.5 × 0.30
= 14 29
Answer:
Total number of determinant of second order with each element being 0 or 1 is 2 4 = 16
The values of determinant is positive in the following cases [ 1 0 0 1 ] , [ 1 1 0 1 ] , [ 1 0 1 1 ]
Probability is
= 3 16
Evaluate the following probabilities
(i) P ( A f a i l s ∣ B h a s f a i l e d )
(ii) P ( A f a i l s a l o n e )
Answer:
(i) Let event in which A fails and B fails be E A , E B
P ( E A ) = 0.2
P ( E A a n d E B ) = 0.15
P ( B f a i l s a l o n e ) = P ( E B ) − P ( E A a n d E B )
⇒ 0.15 = P ( E B ) − 0.15
⇒ P ( E B ) = 0.3
P ( E A | E B ) = P ( E A ∩ E B ) P ( E B )
= 0.15 0.3 = 0.5
(ii) Let the 30622event in which A fails and B fails be E A , E B
P ( E A ) = 0.2
P ( E A a n d E B ) = 0.15
P ( B f a i l s a l o n e ) = P ( E B ) − P ( E A a n d E B )
⇒ 0.15 = P ( E B ) − 0.15
⇒ P ( E B ) = 0.3
P ( A f a i l s a l o n e ) = P ( E A ) − P ( E A a n d E B )
= 0.2 − 0.15 = 0.05
Answer:
Let E1 and E2 respectively denote the event that red ball is transfered from bag 1 to bag 2 and a black ball is transfered from bag 1 to bag2.
P ( E 1 ) = 3 7 and P ( E 2 ) = 4 7
Let A be the event that ball drawn is red.
When a red ball is transfered from bag 1 to bag 2.
P ( A | E 1 ) = 5 10 = 1 2
When a black ball is transfered from bag 1 to bag 2.
P ( A | E 2 ) = 4 10 = 2 5
P ( E 2 | A ) = P ( E 2 ) . P ( A | E 2 ) P ( E 2 ) . P ( A | E 2 ) + P ( E 1 ) . P ( A | E 1 )
= 4 7 × 2 5 4 7 × 2 5 + 3 7 × 1 2
= 16 31
Question 11: If A and B are two events such that P(A≠0) and P(B∣A)=1, then
Choose the correct answer of the following:
Answer:
A and B are two events such that P ( A ≠ 0 ) and P ( B ∣ A ) = 1 ,
P ( B | A ) = P ( B ∩ A ) P ( A )
1 = P ( B ∩ A ) P ( A )
P ( B ∩ A ) = P ( A )
⇒ A ⊂ B
Option A is correct.
Question 12: If P(A∣B)>P(A) , then which of the following is correct :
Answer:
P ( A ∣ B ) > P ( A )
⇒ P ( A ∩ B ) P ( B ) > P ( A )
⇒ P ( A ∩ B ) > P ( A ) . P ( B )
⇒ P ( A ∩ B ) P ( A ) > P ( B )
⇒ P ( B | A ) > P ( B )
Option C is correct.
Question 13: If A and B are any two events such that P(A)+P(B)−P(AandB)=P(A), then
Answer:
P ( A ) + P ( B ) − P ( A a n d B ) = P ( A ) ,
P ( A ) + P ( B ) − P ( A ∩ B ) = P ( A )
⇒ P ( B ) − P ( A ∩ B ) = 0
⇒ P ( B ) = P ( A ∩ B )
P ( A | B ) = P ( A ∩ B ) P ( B ) = P ( B ) P ( B ) = 1
Option B is correct.
Also, read,
- Probability Class 12 Exercise 13.1
- Probability Class 12 Exercise 13.2
- Probability Class 12 Exercise 13.3
- Probability Class 12 Miscellaneous Exercise
Class 12 Maths NCERT Chapter 13: Extra Question
Question: Eight coins are tossed together. The probability of getting exactly 3 heads is:
Solution:
Given:
probability distribution
The total number of coins is tossed,
The probability of getting head,
The probability of getting tail,
The Required probability
Hence, the correct answer is
Approach to Solve Questions of Probability Class 12
- Master the conditional probability formula.
- Understand the types of events, such as simple, compound, mutually exclusive, exhaustive, independent or complementary.
- In case of reverse probability, use Bayes’ theorem. The formula looks a bit complicated, but with adequate practice, it will become simpler.
- In case of a partition of a sample case (when an event depends on several other events), use the total probability theorem.
- Focus on the keywords like “At least”, “only if”, “given”, and “either”.
- Use a Venn diagram for conditional probability when the numbers are small.
What Extra Should Students Study Beyond NCERT for JEE?
Concept Name | JEE | NCERT |
✅ | ||
✅ | ||
✅ | ||
✅ | ||
✅ | ||
✅ | ||
✅ | ✅ | |
✅ | ✅ | |
✅ | ✅ | |
✅ | ✅ | |
✅ | ✅ | |
✅ | ✅ | |
✅ | ✅ | |
✅ | ✅ | |
✅ | ✅ | |
✅ | ✅ | |
✅ |
NCERT Solutions for Class 12 Maths: Chapter Wise
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBookAlso, read,
JEE Main Important Mathematics Formulas
As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
NCERT solutions for class 12 subject-wise
Here are the subject-wise links for the NCERT solutions of class 12:
- NCERT solutions for class 12 mathematics
- NCERT solutions class 12 chemistry
- NCERT solutions for class 12 physics
- NCERT solutions for class 12 biology
NCERT Solutions class-wise
Given below are the class-wise solutions of class 12 NCERT:
- NCERT solutions for class 12
- NCERT solutions for class 11
- NCERT solutions for class 10
- NCERT solutions for class 9
NCERT Books and NCERT Syllabus
Here are some useful links for the NCERT books and the NCERT syllabus for class 12
Frequently Asked Questions (FAQs)
1. How to solve Bayes' Theorem questions in Class 12 Probability?
To solve Bayes' Theorem questions, apply the formula:
P(A | B) = (P(B | A) x P(A)) / P(B)
Here, P(A | B) is the probability of event A given event B, P(B | A) is the probability of event B given A, and P(A) and P(B) are the probabilities of A and B.
2. What is the formula for Conditional Probability in NCERT Class 12 Maths?
The formula for Conditional Probability is:
P(A | B) = P(A ∩ B) / P(B)
where P(A | B) is the probability of A occurring given that B has occurred.
3. What are the basic concepts of Probability in NCERT Class 12 Maths?
The basic concepts include understanding random experiments, sample spaces, events (simple and compound), probability rules (addition and multiplication rules), and probability distributions.
4. How to solve Bernoulli Trials and Binomial Distribution questions?
To solve these questions, use the Binomial Distribution formula:
P(X = k) = (n choose k) x p^k x (1 - p)^(n - k)
where n is the number of trials, k is the number of successes, and p is the probability of success in each trial.
5. What is the difference between Classical and Conditional Probability in NCERT?
Classical Probability is based on equally likely outcomes (i.e., all outcomes are equally probable), while Conditional Probability is the probability of an event occurring given that another event has already occurred. The key difference is that Classical looks at all possible outcomes equally, while Conditional focuses on a subset of outcomes based on additional information.
Also Read
Articles
Upcoming School Exams
Admit Card Date:17 April,2025 - 17 May,2025
Admit Card Date:06 May,2025 - 20 May,2025
Certifications By Top Providers
Digital Banking Business Model
Via State Bank of India Full-Stack Web Development
Via Masai School Banking 101 A Guide for Beginners in the Banking Sector
Via EduBridge Artificial Intelligence Projects
Via Great Learning Business Analytics Foundations
Via PW Skills Edx
1115 coursesCoursera
816 coursesUdemy
394 coursesFuturelearn
295 coursesHarvard University, Cambridge
98 coursesUniversity of Michigan, Ann Arbor
83 coursesExplore Top Universities Across Globe
University of Essex, Colchester
Wivenhoe Park Colchester CO4 3SQUniversity College London, London
Gower Street, London, WC1E 6BTThe University of Edinburgh, Edinburgh
Old College, South Bridge, Edinburgh, Post Code EH8 9YLUniversity of Bristol, Bristol
Beacon House, Queens Road, Bristol, BS8 1QUUniversity of Delaware, Newark
Newark, DE 19716University of Nottingham, Nottingham
University Park, Nottingham NG7 2RDACT Vocabulary Words You Must Know in 2025
21 min ⋆ May 09, 2025 06:05 AM ISTTips 5 ACT Preparation Tips 2025 - Section wise Strategies to Score High
7 min ⋆ May 09, 2025 05:05 AM ISTACT Practice Test 2025 - Download PDF with Answers and Explanations
5 min ⋆ May 09, 2025 05:05 AM ISTMBBS Fees in Bangladesh for Indian Students 2025: Medical Colleges
5 min ⋆ Apr 15, 2025 05:04 AM ISTNew German Student Visa Process: Online Portal at digital.diplo.de for Applications
5 min ⋆ May 09, 2025 03:05 AM ISTLSAT Abroad Sample Papers 2025, Question Paper - Download PDF Here!
4 min ⋆ May 09, 2025 02:05 AM ISTQuestions related to CBSE Class 12th
Have a question related to CBSE Class 12th ?
Changing from the CBSE board to the Odisha CHSE in Class 12 is generally difficult and often not ideal due to differences in syllabi and examination structures. Most boards, including Odisha CHSE , do not recommend switching in the final year of schooling. It is crucial to consult both CBSE and Odisha CHSE authorities for specific policies, but making such a change earlier is advisable to prevent academic complications.
Manasvini Gupta 30 January,2025
Hello there! Thanks for reaching out to us at Careers360.
Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.
Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!
Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.
If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.
Let me know if you need any other tips for your math prep. Good luck with your studies!
Jefferson 25 September,2024
It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.
Possible steps:
-
Re-evaluate Your Study Strategies:
- Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
- Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
- Practice Regularly: Consistent practice is key to mastering chemistry.
-
Consider Professional Help:
- Tutoring: A tutor can provide personalized guidance and support.
- Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.
-
Explore Alternative Options:
- Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
- Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.
-
Focus on NEET 2025 Preparation:
- Stay Dedicated: Continue your NEET preparation with renewed determination.
- Utilize Resources: Make use of study materials, online courses, and mock tests.
-
Seek Support:
- Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
- Join Study Groups: Collaborating with peers can create a supportive learning environment.
Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.
I hope this information helps you.
Kanishka kaushikii 17 September,2024
Hi,
Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.
Scholarship Details:
Type A: For candidates scoring 60% or above in the exam.
Type B: For candidates scoring between 50% and 60%.
Type C: For candidates scoring between 40% and 50%.
Cash Scholarship:
Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).
Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.
Hope you find this useful!
Yuvan 30 August,2024
hello mahima,
If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.
hope this helps.
Ashvadha 12 July,2024
Popular CBSE Class 12th Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Study Resources, Applications and Opportunities
ALLEN Coaching
ApplyRegister for ALLEN Scholarship Test & get up to 90% Scholarship
NEET/JEE Coaching Scholarship
ApplyGet up to 90% Scholarship on Offline NEET/JEE coaching from top Institutes
NEET Most scoring concepts
Get nowThis ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
News and Notifications
16 hours ago :
16 hours ago :
May 12, 2025 - 10:32 PM IST
May 12, 2025 - 08:28 AM IST
CBSE Board Result 2025 LIVE: Class 10th, 12th results by next week; DigiLocker codes, latest updates
May 10, 2025 - 10:27 PM IST
May 10, 2025 - 11:38 AM IST
May 08, 2025 - 05:59 PM IST
May 07, 2025 - 10:54 PM IST
April 18, 2025 - 10:17 AM IST
Stay up-to date with CBSE Class 12th News
Ask
Question
Student Community: Where Questions Find Answers
Back to top