• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Miscellaneous Exercise Chapter 13 Class 12 - Probability

NCERT Solutions for Miscellaneous Exercise Chapter 13 Class 12 - Probability

Edited By Ramraj Saini | Updated on Dec 04, 2023 01:59 PM IST | #CBSE Class 12th
Upcoming Event
CBSE Class 12th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 12 Chapter 13 Miscellaneous Exercise

NCERT Solutions for miscellaneous exercise chapter 13 class 12 Probability are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. NCERT solutions for Class 12 Maths chapter 13 miscellaneous exercise consist of different types of questions covering all the concepts of probability Class 12 Maths NCERT syllabus. These questions can be practised, if you have solved all the previous NCERT book chapter 13 exercises. Miscellaneous exercise chapter 13 Class 13 questions are a bit difficult than all the previous exercises questions. You are advised to solve all exercise questions by yourself. If you find difficulties while solving them, you can go through NCERT solutions for Class 12 Maths chapter 13 miscellaneous exercise.

There are very few questions asked in the board exams from miscellaneous exercises, it is not considered to be very important for board exams. You can solve these exercises to be on the safer side in the board exams. Miscellaneous exercise class 12 chapter 13 are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise enumerated in NCERT Book together using the link provided below.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Probability Class 12 Chapter 13-Miscellaneous Exercise

Question:1(i) A and B are two events such thatP(A)\neq 0. Find P(B\mid A), if

A is a subset of B

Answer:

A and B are two events such thatP(A)\neq 0.

A\subset B

\Rightarrow \, \, \, \, A\cap B=A

P(A\cap B)=P(B\cap A)=P(A)

P(B|A)=\frac{P(B\cap A)}{P(A)}

P(B|A)=\frac{P( A)}{P(A)}

P(B|A)=1

Question:1(ii) A and B are two events such that P(A)\neq 0. Find P(B\mid A), if

A\cap B=\phi

Answer:

A and B are two events such thatP(A)\neq 0.

P(A\cap B)=P(B\cap A)=0

P(B|A)=\frac{P(B\cap A)}{P(A)}

P(B|A)=\frac{0}{P(A)}

P(B|A)=0

Question:2(i) A couple has two children,

Find the probability that both children are males, if it is known that at least one of the children is male.

Answer:

A couple has two children,

sample space =\left \{ (b,b),(g,g),(b,g),(g,b) \right \}

Let A be both children are males and B is at least one of the children is male.

(A\cap B)=\left \{ (b,b) \right \}

P(A\cap B)=\frac{1}{4}

P(A)=\frac{1}{4}

P(B)=\frac{3}{4}

P(A|B)=\frac{P(A\cap B)}{P(B)}

P(A|B)=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}

Question:2(ii) A couple has two children,

Find the probability that both children are females, if it is known that the elder child is a female.

Answer:

A couple has two children,

sample space =\left \{ (b,b),(g,g),(b,g),(g,b) \right \}

Let A be both children are females and B be the elder child is a female.

(A\cap B)=\left \{ (g,g) \right \}

P(A\cap B)=\frac{1}{4}

P(A)=\frac{1}{4}

P(B)=\frac{2}{4}

P(A|B)=\frac{P(A\cap B)}{P(B)}

P(A|B)=\frac{\frac{1}{4}}{\frac{2}{4}}=\frac{1}{2}

Question:3 Suppose that 5^{o}/_{o} of men and 0.25^{o}/_{o} of women have grey hair. A grey haired person is selected at random. What is the probability of this person being male? Assume that there are equal number of males and females.

Answer:

We have 5^{o}/_{o} of men and 0.25^{o}/_{o} of women have grey hair.

Percentage of people with grey hairs =(5+0.25)\%=5.25\%

The probability that the selected haired person is male :

=\frac{5}{5.25}=\frac{20}{21}

Question:4 Suppose that 90^{o}/_{o} of people are right-handed. What is the probability that at most 6 of a random sample of 10 people are right-handed?

Answer:

90^{o}/_{o} of people are right-handed.

P(right-handed)=\frac{9}{10}

P(left-handed)=q=1-\frac{9}{10}=\frac{1}{10}

at most 6 of a random sample of 10 people are right-handed.

the probability that more than 6 of a random sample of 10 people are right-handed is given by,

^{10}C_rP^{r}q^{10-r}

=\sum_{T}^{10}^{10} C_r\frac{9}{10}^r .(\frac{1}{10})^{10-r}

the probability that at most 6 of a random sample of 10 people are right-handed is given by

=1-\sum_{T}^{10}^{10}C_r .\frac{9}{10}^r .(\frac{1}{10})^{10-r}

Question:5(i) An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y' A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that

all will bear 'X' mark.

Answer:

Total balls in urn = 25

Balls bearing mark 'X' =10

Balls bearing mark 'Y' =15

P(ball\, \, bearing\, mark\, 'X')=\frac{10}{25}=\frac{2}{5}

P(ball\, \, bearing\, mark\, 'Y')=\frac{15}{25}=\frac{3}{5}

6 balls are drawn with replacement.

Let Z be a random variable that represents a number of balls with Y mark on them in the trial.

Z has a binomial distribution with n=6.

P(Z=z)=^nC_Z P^{n-Z}q^Z

P(Z=0)=^6C_0 (\frac{2}{5})^{6} \frac{3}{5}^0

P(Z=0)=^6C_0 (\frac{2}{5})^{6}

Question:5(ii) An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that

not more than 2 will bear 'Y' mark.

Answer:

Total balls in urn = 25

Balls bearing mark 'X' =10

Balls bearing mark 'Y' =15

P(ball\, \, bearing\, mark\, 'X')=\frac{10}{25}=\frac{2}{5}

P(ball\, \, bearing\, mark\, 'Y')=\frac{15}{25}=\frac{3}{5}

6 balls are drawn with replacement.

Let Z be random variable that represents number of balls with Y mark on them in trial.

Z has binomail distribution with n=6.

P(Z=z)=^nC_Z P^{n-Z}q^Z

P(not\, more\, than\, 2\, bear\, Y) =P(Z\leq 2)

=P(Z=0)+P(Z=1)+P(Z=2)

=^6C_0 (\frac{2}{5})^{6} (\frac{3}{5})^0+^6C_1 (\frac{2}{5})^{5} (\frac{3}{5})^1+^6C_2 (\frac{2}{5})^{4} (\frac{3}{5})^2

= (\frac{2}{5})^{6} +6 (\frac{2}{5})^{5} (\frac{3}{5})^1+15 (\frac{2}{5})^{4} (\frac{3}{5})^2

= (\frac{2}{5})^{4} [(\frac{2}{5})^{2}+6 (\frac{2}{5}) (\frac{3}{5})+15(\frac{3}{5})^2]

= (\frac{2}{5})^{4} [\frac{4}{25}+\frac{36}{25}+\frac{135}{25}]

= (\frac{2}{5})^{4} [\frac{175}{25}]

= (\frac{2}{5})^{4} [7]

Question:5(iii) An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that

at least one ball will bear 'Y' mark.

Answer:

P(atleast\, one\, bear\, \, Y\, mark) =P(Z\geq 1)=1-P(Z=0)

=1-(\frac{2}{5})^6

Question:5(iv) An urn contains 25 balls of which 10 balls bear a mark 'X' and the remaining 15 bear a mark 'Y'. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that

the number of balls with 'X' mark and 'Y' mark will be equal.

Answer:

P(equal\, to\, the \, number\, of\, balls \, with \, X \, mark \, and\, Y \, mark )=P(Z=3)

P(Z=3)=^6C_3.(\frac{2}{5})^2.(\frac{3}{5})^3

P(Z=3)=\frac{20\times 8\times 27}{15625}

P(Z=3)=\frac{864}{3125}

Question:6 In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is \frac{5}{6} . What is the probability that he will knock down fewer than 2 hurdles?

Answer:

Let p and q respectively be probability that the player will clear and knock down the hurdle.

p=\frac{5}{6}

q=1-p=1-\frac{5}{6}=\frac{1}{6}

Let X represent random variable that represent number of times the player will knock down the hurdle.

P(Z=z)=^nC_Z P^{n-Z}q^Z

P(Z< 2)=P(Z=0)+P(Z=1)

=^{10}C_0 .( \frac{5}{6})^{10}.( \frac{1}{6})^{0}+^{10}C_1 .( \frac{5}{6})^{9}.( \frac{1}{6})^{1}

=( \frac{5}{6})^{10}+10.( \frac{5}{6})^{9}.( \frac{1}{6})

=( \frac{5}{6})^{9}( \frac{5}{6}+10\times . \frac{1}{6})

=( \frac{5}{6})^{9} \times \frac{5}{2}

=\frac{5^1^0}{2\times 6^9}

Question:7 A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.

Answer:

Probability of 6 in a throw of die =P

P=\frac{1}{6}

q=1-P=1-\frac{1}{6}=\frac{5}{6}

Probability that 2 sixes come in first five throw of die :

=^5C_2 (\frac{5}{6})^3 (\frac{1}{6})^2

=\frac{10\times 5^3}{6^5}

Probability that third six comes in sixth throw :

=\frac{10\times 5^3}{6^5}\times \frac{1}{6}

=\frac{10\times 125}{6^6}

=\frac{1250}{23328}

Question:8 If a leap year is selected at random, what is the chance that it will contain 53 tuesdays?

Answer:

In a leap year, there are 366 days.

In 52 weeks, there are 52 Tuesdays.

The probability that a leap year will have 53 Tuesday is equal to the probability that the remaining 2 days are Tuesday.

The remaining 2 days can be :

1. Monday and Tuesday

2. Tuesday and Wednesday

3. Wednesday and Thursday

4. Thursday and Friday

5.friday and Saturday

6.saturday and Sunday

7.sunday and Monday

Total cases = 7.

Favorable cases = 2

Probability of having 53 Tuesday in a leap year = P.

P=\frac{2}{7}

Question:9 An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be atleast 4 successes.

Answer:

Probability of success is twice the probability of failure.

Let probability of failure be X

then Probability of success = 2X

Sum of probabilities is 1.

\therefore \, \, \, X+2X=1

\Rightarrow \, \, \, 3X=1

\Rightarrow \, \, \, X=\frac{1}{3}

Let P=\frac{1}{3} and q=\frac{2}{3}

Let X be random variable that represent the number of success in six trials.

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

P(X\geq 4)=P(X=4)+P(X=5)+P(X=6)

=^6C_4 \left [ \frac{2}{3} \right ]^4\left [ \frac{1}{3} \right ]^2+^6C_5 \left [ \frac{2}{3} \right ]^5\left [ \frac{1}{3} \right ]^1+^6C_6 \left [ \frac{2}{3} \right ]^6\left [ \frac{1}{3} \right ]^0

=\frac{15\times 2^4}{3^6}+\frac{6\times 2^5}{3^6}+\frac{2^6}{3^6}

=\frac{ 2^6}{3^6}(15+12+4)

=\frac{ 2^6}{3^6}(31)

=\frac{31}{9}\left [ \frac{2}{3} \right ]^4

Question:10 How many times must a man toss a fair coin so that the probability of having at least one head is more than 90^{o}/_{o} ?

Answer:

Let the man toss coin n times.

Probability of getting head in first toss = P

P=\frac{1}{2}

q=\frac{1}{2}

\therefore \, \, \, \, P(X=x)=^nC_x.q^{n-x}.p^x

=^nC_x.\left ( \frac{1}{2} \right )^{n-x}.\left ( \frac{1}{2} \right )^x

P(getting\, atleast\, one\, head)> \frac{90}{100}

P(X\geq 1)> 0.9

1-P(X=0)> 0.9

1-^nC_0 \frac{1}{2^n}> 0.9

^nC_0 \frac{1}{2^n}< 0.1

\frac{1}{2^n}< 0.1

\frac{1}{0.1}< 2^n

10< 2^n

The minimum value to satisfy the equation is 4.

The man should toss a coin 4 or more times.

Question:11 In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins / loses.

Answer:

In a throw of die,

probability of getting six = P

P=\frac{1}{6}

probability of not getting six = q

q=1-P=1-\frac{1}{6}=\frac{5}{6}

There are three cases :

1. Gets six in the first throw, required probability is \frac{1}{6}

The amount he will receive is Re. 1

2.. Does not gets six in the first throw and gets six in the second throw, then the probability

=\frac{5}{6}\times \frac{1}{6}=\frac{5}{36}

The amount he will receive is - Re.1+ Re.1=0

3. Does not gets six in first 2 throws and gets six in the third throw, then the probability

=\frac{5}{6}\times\frac{5}{6}\times \frac{1}{6}=\frac{25}{216}

Amount he will receive is -Re.1 - Re.1+ Re.1= -1

Expected value he can win :

=1\times \frac{1}{6}+0\times \frac{5}{36}+(-1)\times \frac{25}{216}

= \frac{1}{6}-\frac{25}{216}

= \frac{11}{216}

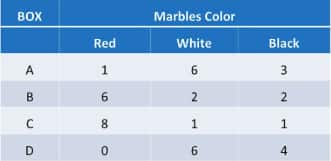
Question:12(i) Suppose we have four boxes A,B,C and D containing coloured marbles as given below:

One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A ?

Answer:

'

Let R be the event of drawing red marble.

Let E_A,E_B,E_C respectively denote the event of selecting box A, B, C.

Total marbles = 40

Red marbles =15

P(R)=\frac{15}{40}=\frac{3}{8}

Probability of drawing red marble from box A is P(E_A|R)

P(E_A|R)=\frac{P(E_A\cap R)}{P(R)}

=\frac{\frac{1}{40}}{\frac{3}{8}}

=\frac{1}{15}

Question:12(ii) Suppose we have four boxes A,B,C and D containing coloured marbles as given below:

One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box B?

Answer:

Let R be event of drawing red marble.

Let E_A,E_B,E_C respectivly denote event of selecting box A,B,C.

Total marbles = 40

Red marbles =15

P(R)=\frac{15}{40}=\frac{3}{8}

Probability of drawing red marble from box B is P(E_B|R)

P(E_B|R)=\frac{P(E_B\cap R)}{P(R)}

=\frac{\frac{6}{40}}{\frac{3}{8}}

=\frac{2}{5}

Question:12(iii) Suppose we have four boxes A,B,C and D containing coloured marbles as given below:

One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box C?

Answer:

Let R be event of drawing red marble.

Let E_A,E_B,E_C respectivly denote event of selecting box A,B,C.

Total marbles = 40

Red marbles =15

P(R)=\frac{15}{40}=\frac{3}{8}

Probability of drawing red marble from box C is P(E_C|R)

P(E_C|R)=\frac{P(E_C\cap R)}{P(R)}

=\frac{\frac{8}{40}}{\frac{3}{8}}

=\frac{8}{15}

Question:13 Assume that the chances of a patient having a heart attack is 40^{o}/_{o}. It is also assumed that a meditation and yoga course reduce the risk of heart attack by 30^{o}/_{o} and prescription of certain drug reduces its chances by 25^{o}/_{o}.At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?

Answer:

Let A,E1, E2 respectively denote the event that a person has a heart break, selected person followed the course of yoga and meditation , and the person adopted

the drug prescription.

\therefore \, \, \, \, P(A)=0.40

\therefore \, \, \, \, P(E1)=P(E2)=\frac{1}{2}

P(A|E1)=0.40\times 0.70=0.28

P(A|E2)=0.40\times 0.75=0.30

the probability that the patient followed a course of meditation and yoga is P(E1,A)

P(E1,A)=\frac{P(E1).P(E1|A)}{P(E1).P(E1|A)+P(E2).P(E2|A)}

P(E1,A)=\frac{0.5\times 0.28}{0.5\times 0.28 + 0.5\times 0.30}

=\frac{14}{29}

Question:14 If each element of a second order determinant is either zero or one, what is the probability that the value of the determinant is positive? (Assume that the individual entries of the determinant are chosen independently, each value being assumed with probability \frac{1}{2} ).

Answer:

Total number of determinant of second order with each element being 0 or 1 is 2^4=16

The values of determinant is positive in the following cases \begin{bmatrix} 1 & 0\\ 0 & 1\end{bmatrix}, \begin{bmatrix} 1 & 1\\ 0 & 1\end{bmatrix}, \begin{bmatrix} 1 & 0\\ 1 & 1\end{bmatrix}

Probability is

=\frac{3}{16}

Question:15(i) An electronic assembly consists of two subsystems, say, A and B. From previous testing procedures, the following probabilities are assumed to be known:

P(A fails) =0.2

P(B fails alone) = 0.15

P(A and B fail) = 0.15

Evaluate the following probabilities

P(A \; fails\mid B\; has\; failed)

Answer:

Let event in which A fails and B fails be E_A,E_B

P(E_A)=0.2

P(E_A\, and \, E_B)=0.15

P(B\, fails\, alone)=P(E_B)-P(E_A\, and\, E_B)

\Rightarrow \, \, \, 0.15=P(E_B)-0.15

\Rightarrow \, \, \, P(E_B)=0.3

P(E_A|E_B)=\frac{P(E_A\cap E_B)}{P(E_B)}

=\frac{0.15}{0.3}=0.5

Question:15(ii) An electronic assembly consists of two subsystems, say, A and B. From previous testing procedures, the following probabilities are assumed to be known:

P(A fails) = 0.2

P(B fails alone) = 0.15

P(A and B fail) = 0.15

Evaluate the following probabilities

P(A\; fails \; alone)

Answer:

Let event in which A fails and B fails be E_A,E_B

P(E_A)=0.2

P(E_A\, and \, E_B)=0.15

P(B\, fails\, alone)=P(E_B)-P(E_A\, and\, E_B)

\Rightarrow \, \, \, 0.15=P(E_B)-0.15

\Rightarrow \, \, \, P(E_B)=0.3

P(A\, fails\, \, alone)=P(E_A)-P(E_A\, and\, E_B)

=0.2-0.15=0.05

Question:16 Bag I contains 3 red and 4 black balls and Bag II contains 4 red and 5 black balls. One ball is transferred from Bag I to Bag II and then a ball is drawn from Bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred ball is black.

Answer:

Let E1 and E2 respectively denote the event that red ball is transfered from bag 1 to bag 2 and a black ball is transfered from bag 1 to bag2.

P(E1)=\frac{3}{7} and P(E2)=\frac{4}{7}

Let A be the event that ball drawn is red.

When a red ball is transfered from bag 1 to bag 2.

P(A|E1)=\frac{5}{10}=\frac{1}{2}

When a black ball is transfered from bag 1 to bag 2.

P(A|E2)=\frac{4}{10}=\frac{2}{5}

P(E2|A)=\frac{P(E2).P(A|E2)}{P(E2).P(A|E2)+P(E1).P(A|E1)}

=\frac{\frac{4}{7}\times \frac{2}{5}}{\frac{4}{7}\times \frac{2}{5}+\frac{3}{7}\times \frac{1}{2}}

=\frac{16}{31}

Question:17 If A and B are two events such that P(A\neq 0) andP(B\mid A)=1, then

Choose the correct answer of the following:

(A) A\subset B

(B) B\subset A

(C) B=\phi

(D) A=\phi

Answer:

A and B are two events such that P(A\neq 0) andP(B\mid A)=1,

P(B|A)=\frac{P(B\cap A)}{P(A)}

1=\frac{P(B\cap A)}{P(A)}

P(B\cap A)=P(A)

\Rightarrow \, \, \, A\subset B

Option A is correct.

Question:18 If P(A\mid B)> P(A), then which of the following is correct :

(A) P(B\mid A)< P(B)

(B) P(A\cap B)< P(A).P(B)

(C) P(B\mid A)> P(B)

(D)P(B\mid A)= P(B)

Answer:

P(A\mid B)> P(A)

\Rightarrow \, \, \frac{P(A\cap B)}{P(B)}> P(A)

\Rightarrow \, \, P(A\cap B)> P(A).P(B)

\Rightarrow \, \, \frac{P(A\cap B)}{P(A)}> P(B)

\Rightarrow \, \, P(B|A)> P(B)

Option C is correct.

Question:19 If A and B are any two events such that P(A)+P(B)-P(A \; and\; B)=P(A), then

(A) P(B\mid A)=1

(B) P(A\mid B)=1

(C) P(B\mid A)=0

(D) P(A\mid B)=0

Answer:

P(A)+P(B)-P(A \; and\; B)=P(A),

P(A)+P(B)-P(A\cap B)=P(A)

\Rightarrow \, \, \, P(B)-P(A\cap B)=0

\Rightarrow \, \, \, P(B)=P(A\cap B)

P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{P(B)}{P(B)}=1

Option B is correct.

More About NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise:-

As the name suggests NCERT solutions for Class 12 Maths chapter 13 miscellaneous exercise consist of different types of questions from all the previous exercises of the probability. This exercise is considered to be tough as compared to the previous exercises but it is not as important as previous exercises of this chapter for board exams. There are very few questions in board exams that are asked from miscellaneous exercises but it is very important for competitive exams. Students are advised to solve this exercise also to get command on the concept.

Benefits of NCERT Solutions for Class 12 Maths Chapter 13 Miscellaneous Exercise:-

  • NCERT solutions for Class 12 Maths chapter 13 miscellaneous exercise are explained in a very detailed manner, so you can understand them very easily.
  • There are 19 questions and 5 examples given in the miscellaneous exercise which you can solve to get a command on the probability theory.
  • NCERT solutions for Class 12 Maths chapter 13 miscellaneous exercise are very helpful for the students who are preparing for the competitive exams.
  • Miscellaneous exercise chapter 13 Class 12 is a mixture of the questions from probability theory which will check your understanding of the concept.
  • NCERT solutions for Class 12 Maths chapter 13 miscellaneous Exercise can be used for reference.
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Key Features Of NCERT Solutions For Class 12 Chapter 13 Miscellaneous Exercise

  • Comprehensive Coverage: The solutions encompass all the topics covered in miscellaneous exercise class 12 chapter 13, ensuring a thorough understanding of the concepts.
  • Step-by-Step Solutions: In this class 12 chapter 13 maths miscellaneous solutions, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
  • Accuracy and Clarity: Solutions for class 12 maths miscellaneous exercise chapter 13 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
  • Conceptual Clarity: In this class 12 maths ch 13 miscellaneous exercise solutions, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
  • Inclusive Approach: Solutions for class 12 chapter 13 miscellaneous exercise cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
  • Relevance to Curriculum: The solutions for miscellaneous exercise class 12 chapter 13 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions of Class 12 Subject Wise

Subject Wise NCERT Exampler Solutions

Happy learning!!!

Frequently Asked Questions (FAQs)

1. Do questions from the miscellaneous exercises comes in 12th board exams?

More than 95% of questions in the board's exam are not asked from miscellaneous exercises but it is very important for competitive exams.

2. What are the topics in miscellaneous exercise probability Class 12 ?

Miscellaneous exercise is consists of different questions from all the topics of probability Class 12 Maths.

3. What is the probability of an impossible event ?

The probability of an impossible event is 0.

4. What is the probability of getting 0 when we roll a die ?

The probability of getting 0 when we roll a die is zero.

5. What is the probability of getting number less than 7 when we roll a die ?

The probability of a number less than 7 when we roll a die is one.

6. Give an example of certain event .

The event of getting a number less than 7 when we roll a die is an example of a certain event.

7. Give an example of impossible event ?

The event of getting number 0 we roll a die is an example of an impossible event.

8. Where can I get NCERT solutions ?

Here you can get NCERT Solutions.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Gujarat Board Secondary School Certificate Examination

Late Fee Application Date:11 December,2024 - 20 December,2024

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Business Analytics Foundations
 Via PW Skills
Digital Banking Business Model
 Via State Bank of India
Full-Stack Android Development
 Via Masai School
Data Science for Beginners
 Via Board Infinity
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer
Jefferson 25 September,2024
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

  1. Re-evaluate Your Study Strategies:

    • Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
    • Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
    • Practice Regularly: Consistent practice is key to mastering chemistry.

  2. Consider Professional Help:

    • Tutoring: A tutor can provide personalized guidance and support.
    • Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.

  3. Explore Alternative Options:

    • Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
    • Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.

  4. Focus on NEET 2025 Preparation:

    • Stay Dedicated: Continue your NEET preparation with renewed determination.
    • Utilize Resources: Make use of study materials, online courses, and mock tests.

  5. Seek Support:

    • Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
    • Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.







Read Complete Answer
Kanishka kaushikii 17 September,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer
Yuvan 30 August,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
November 20, 2024 - 11:17 PM IST :
Board Exams: States agree to equivalence; no question paper ‘jumbling’ from next year, says PARAKH CEO
December 12, 2024 - 12:44 PM IST
Board Exam Date 2025 Live: CBSE, ICSE, BSEB, MPBSE Class 10, 12 timetable out; Punjab, Rajasthan schedule soon
December 08, 2024 - 10:34 PM IST
CBSE Board Exams 2025: Guidelines issued for Class 10, 12 practicals
December 03, 2024 - 01:11 PM IST
Board Exam Date Sheet 2025 Live: ICSE, ISC, CBSE, MP time table out; BSEB routine soon
November 26, 2024 - 10:18 PM IST
Board exam dates 2025: CBSE, CISCE, UP, MP, Maharashtra, TN time table out; state-wise updates
November 25, 2024 - 08:42 PM IST
Board Exam Date Sheet 2025: CBSE, UPMSP, MPBSE, Class 10, 12 board exam dates out; BSEB, CGBSE schedules soon
November 22, 2024 - 10:04 PM IST
CBSE Date Sheet 2025 (Out) Live: Class 10, 12 board exam time table at cbse.gov.in; syllabus, sample papers
November 21, 2024 - 09:30 PM IST

Stay up-to date with CBSE Class 12th News

Back to top