NCERT Application Of Integrals Class 12 Questions And Answers (Exercise)
|
Class 12 Maths Chapter 8 Solutions Exercise: 8.1
Page number: 296
Total questions: 4
|
Question 1: Find the area of the region bounded by the ellipse $\frac{x^2}{16}+\frac{y^2}{9}=1.$
Answer:
The area bounded by the ellipse : $\frac{x^2}{16}+\frac{y^2}{9}=1$
The area will be 4 times the area of EAB.
Therefore, $Area\ of\ EAB= \int^4_{0} y dx$
$= \int^4_{0}3\sqrt{1-\frac{x^2}{16}} dx$
$= \frac{3}{4}\int^4_{0}\sqrt{16-x^2} dx$
$= \frac{3}{4}\left [ \frac{x}{2}\sqrt{16-x^2}+\frac{16}{2}\sin^{-1}\frac{x}{4} \right ]^4_{0}$
$= \frac{3}{4}\left [ 2\sqrt{16-16} +8\sin^{-1}(1)-0-8\sin^{-1}(0)\right ]$
$= \frac{3}{4}\left [ \frac{8\pi}{2} \right ]$
$= \frac{3}{4}\left [ 4\pi \right ] =3\pi$
Therefore, the area bounded by the ellipse will be $= 4\times {3\pi} = 12\pi\ units.$
Question 2: Find the area of the region bounded by the ellipse $\small \frac{x^2}{4}+\frac{y^2}{9}=1$
Answer:
The area bounded by the ellipse : $\small \frac{x^2}{4}+\frac{y^2}{9}=1$
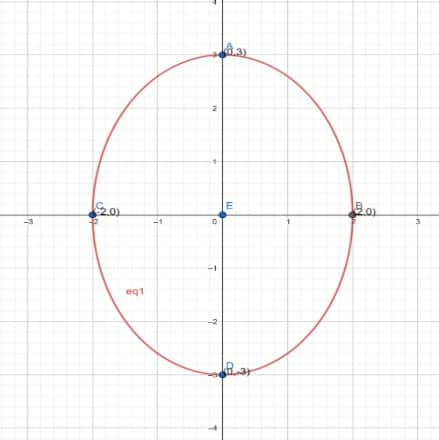
The area will be 4 times the area of EAB.
Therefore, $Area\ of\ EAB= \int^2_{0} y dx$
$= \int^2_{0}3\sqrt{1-\frac{x^2}{4}} dx$
$= \frac{3}{2}\int^2_{0}\sqrt{4-x^2} dx$
$= \frac{3}{2}\left [ \frac{x}{2}\sqrt4-x^2 +\frac{4}{2}\sin^{-1}\frac{x}{2} \right ]^2_{0}$
$= \frac{3}{2}\left [ \frac{2\pi}{2} \right ]$
$= \frac{3\pi}{2}$
Therefore, the area bounded by the ellipse will be $= 4\times \frac{3\pi}{2} = 6\pi\ units.$
Question 3: Choose the correct answer in the following
The area lying in the first quadrant and bounded by the circle $\small x^2+y^2=4$ and the lines $\small x=0$ and $\small x=2$ is
$\small(A)\hspace{1mm}\pi$ $\small(B)\hspace{1mm}\frac{\pi}{2}$ $\small (C)\hspace{1mm}\frac{\pi }{3}$ $\small (D)\hspace{1mm}\frac{\pi }{4}$
Answer:
The correct answer is A
The area bounded by circle C(0,0,4) and the line x=2 is
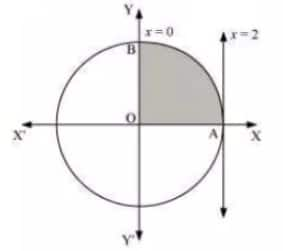
The required area = area of OAB
$\int^2_0ydx = \int^2_0\sqrt{4-x^2}dx$
$\\=[\frac{x}{2}\sqrt{4-x^2}+\frac{4}{2}\sin^{-1}\frac{x}{2}]^2_0\\ =2(\pi/2)\\ =\pi$
Question 4: Choose the correct answer in the following.
Area of the region bounded by the curve $\small y^2=4x$ , $\small y$ -axis and the line $\small y=3$ is
(A) $\small 2$ (B) $\small \frac{9}{4}$ (C) $\small \frac{9}{3}$ (D) $\small \frac{9}{2}$
Answer:
The area bounded by the curve $y^2=4x$ and y =3
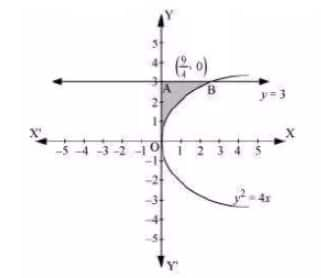
The required area = OAB =
$\\\int ^3_0xdy\\ =\int ^3_0\frac{y^2}{4}dy\\ =\frac{1}{4}.[\frac{y^3}{3}]^3_0\\ =\frac{9}{4}$
|
NCERT Application of Integrals Class 12 Solutions: Exercise: Miscellaneous Exercise
Page Number: 298
Total Questions: 5
|
Question 1: Find the area under the given curves and given lines:
(i) $\small y=x^2,x=1,x=2$ and $\small x$ -axis
Answer:
The area bounded by the curve $\small y=x^2,x=1,x=2$ and $\small x$ -axis
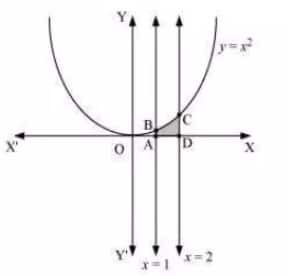
The area of the required region = area of ABCD
$\\=\int_{1}^{2}ydx\\ =\int_{1}^{2}x^2dx\\ =[\frac{x^3}{3}]_1^2\\ =\frac{7}{3}$
Hence, the area of the shaded region is 7/3 units.
Question 1: Find the area under the given curves and given lines:
(ii) $\small y=x^4,x=1,x=5$ and $\small x$ -axis
Answer:
The area bounded by the curev $\small y=x^4,x=1,x=5$ and $\small x$ -axis
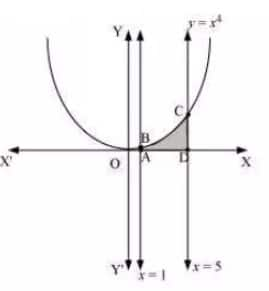
The area of the required region = area of ABCD
$\\=\int_{1}^{5}ydx\\ =\int_{1}^{2}x^4dx\\ =[\frac{x^5}{5}]_1^2\\ =625-\frac{1}{5}\\ =624.8$
Hence, the area of the shaded region is 624.8 units.
Question 2: Sketch the graph of $\small y=|x+3|$ and evaluate $\small \int_{-6}^{0}|x+3|dx.$
Answer:
y=|x+3|
The given modulus function can be written as
x+3>0
x>-3
for x>-3
y=|x+3|=x+3
x+3<0
x<-3
For x<-3
y=|x+3|=-(x+3)
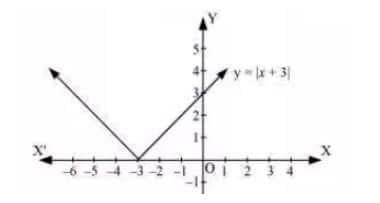
The integral to be evaluated is
$\\\int_{-6}^{0}|x+3|dx$
$=\int_{-6}^{-3}(-x-3)dx+\int_{-3}^{0}(x+3)dx$
$ =[-\frac{x^{2}}{2}-3x]_{-6}^{-3}+[\frac{x^{2}}{2}+3x]_{-3}^{0}$
$=(-\frac{9}{2}+9)-(-18+18)+0-(\frac{9}{2}-9)\\ =9$
Question 3: Find the area bounded by the curve $\small y=\sin x$ between $\small x=0$ and $\small x=2\pi$.
Answer:
The graph of y=sinx is as follows
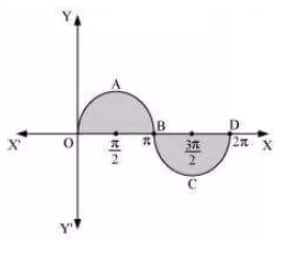
We need to find the area of the shaded region.
ar(OAB)+ar(BCD)
=2ar(OAB)
$\\=2\times \int_{0}^{\pi }sinxdx\\ =2\times [-cosx]_{0}^{\pi }\\ =2\times [-(-1)-(-1)]\\ =4$
The bounded area is 4 units.
Question 4: Choose the correct answer.
Area bounded by the curve $\small y=x^3$ , the $\small x$ -axis and the ordinates $\small x=-2$ and $\small x=1$ is
(A) $\small -9$ (B) $\small \frac{-15}{4}$ (C) $\small \frac{15}{4}$ (D) $\small \frac{17}{4}$
Answer:
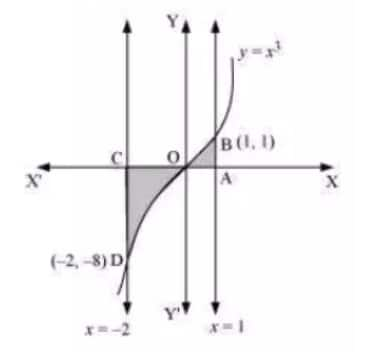
Hence, the required area
$=\int_{-2}^1 ydx$
$=\int_{-2}^1 x^3dx = \left [ \frac{x^4}{4} \right ]_{-2}^1$
$= \left [ \frac{x^4}{4} \right ]^0_{-2} + \left [ \frac{x^4}{4} \right ]^1_{0}$
$= \left [ 0-\frac{(-2)^4}{4} \right ] + \left [ \frac{1}{4} - 0 \right ]$
$= -4+\frac{1}{4} = \frac{-15}{4}$
Therefore, the correct answer is B.
Question 5: Choose the correct answer.
The area bounded by the curve $\small y=x|x|$ , $\small x$ -axis and the ordinates $\small x=-1$ and $\small x=1$ is given by
(A) $\small 0$ (B) $\small \frac{1}{3}$ (C) $\small \frac{2}{3}$ (D) $\small \frac{4}{3}$
[ Hint : $y=x^2$ if $x> 0$ and $y=-x^2$ if $x<0$ . ]
Answer:
The required area is
$\\2\int_{0}^{1}x^{2}dx\\ =2\left [ \frac{x^{3}}{3} \right ]_{0}^{1}\\ =\frac{2}{3}\ units$
Also, read,
