NCERT Solutions for Class 12 Maths Chapter 8 Exercise 8.1 - Application of Integrals
Application of Integrals is like your favourite colouring brush that can fill any shape under every curve, no matter how abstract the shape is. It is a fundamental part of calculus that can help us calculate the area of a certain region, even with no straight sides. In exercise 8.1 of the chapter Application of Integrals, we go beyond the basics of integration and learn about how it's used in our real-life situations, like finding the area of a region or calculating the total distance travelled between two specific points. This article about the NCERT Solutions for Exercise 8.1 of Class 12 Maths, Chapter 8 - Application of Integrals, offers detailed and easy-to-understand solutions for the exercise problems, so that students can clear their doubts and understand the logic behind the solutions. For syllabus, notes, exemplar solutions and PDF, refer to this link: NCERT.
This Story also Contains
- Class 12 Maths Chapter 8 Exercise 8.1 Solutions: Download PDF
- Application of Integrals Class 12 Chapter 8 Exercise: 8.1
- Topics covered in Chapter 8, Application of Integrals: Exercise 8.1
- NCERT Solutions Subject Wise
- NCERT Exemplar Solutions Subject Wise
Class 12 Maths Chapter 8 Exercise 8.1 Solutions: Download PDF
Application of Integrals Class 12 Chapter 8 Exercise: 8.1
Question:1 Find the area of the region bounded by the ellipse $\frac{x^2}{16}+\frac{y^2}{9}=1.$
Answer:
The area bounded by the ellipse : $\frac{x^2}{16}+\frac{y^2}{9}=1.$
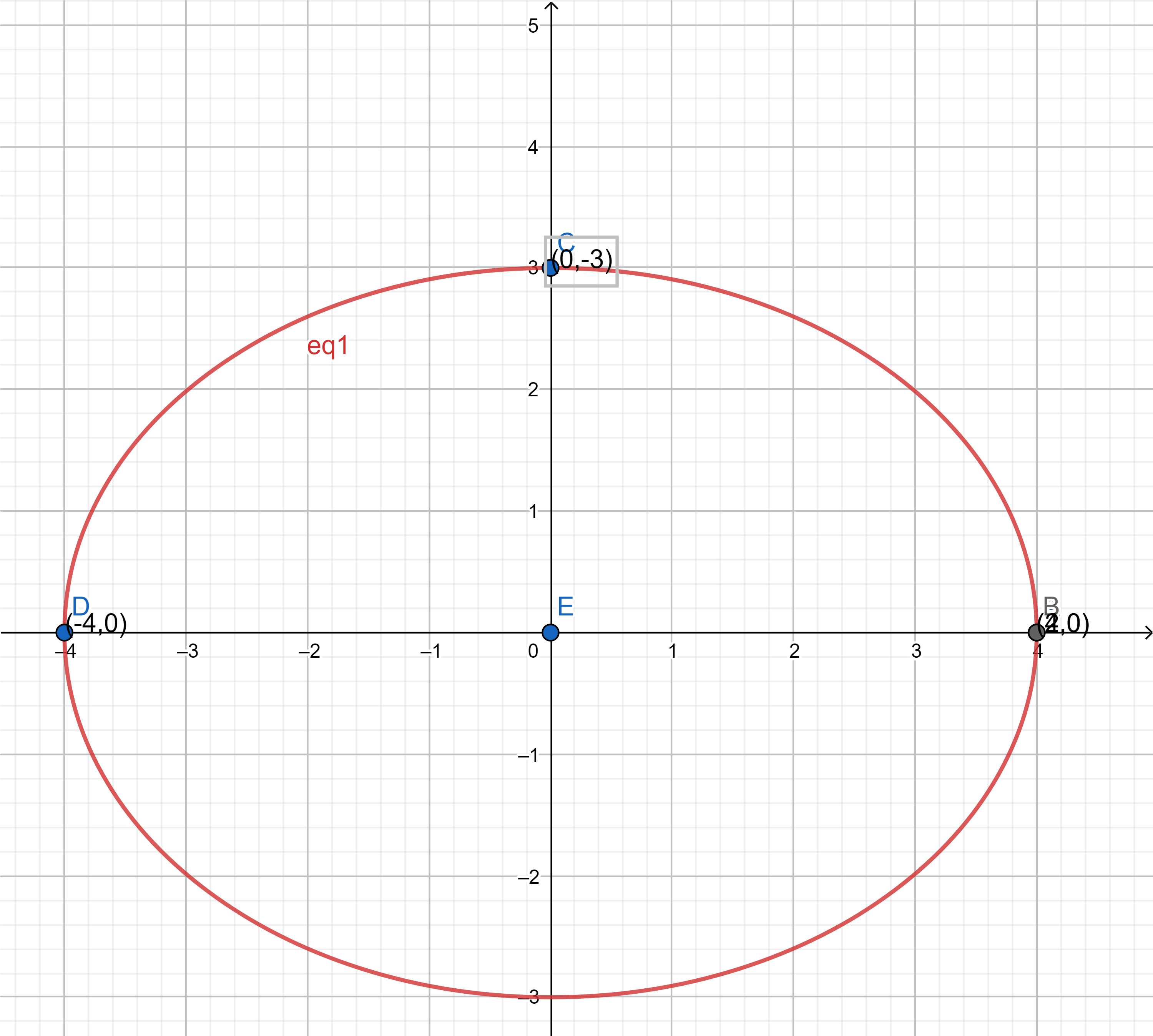
Area will be 4 times the area of EAB.
Therefore, Area of EAB = $\int_0^4 y\,dx$
$= \int^4_{0}3\sqrt{1-\frac{x^2}{16}} dx$
$= \frac{3}{4}\int^4_{0}\sqrt{16-x^2} dx$
$= \frac{3}{4}\left [ \frac{x}{2}\sqrt{16-x^2}+\frac{16}{2}\sin^{-1}\frac{x}{4} \right ]^4_{0}$
$= \frac{3}{4}\left [ 2\sqrt{16-16} +8\sin^{-1}(1)-0-8\sin^{-1}(0)\right ]$
$= \frac{3}{4}\left [ \frac{8\pi}{2} \right ]$
$= \frac{3}{4}\left [ 4\pi \right ] =3\pi$
Therefore, the area bounded by the ellipse will be $= 4 \times 3\pi = 12\pi$ units.
Question 2: Find the area of the region bounded by the ellipse $\small \frac{x^2}{4}+\frac{y^2}{9}=1$
Answer:
The area bounded by the ellipse : $\small \frac{x^2}{4}+\frac{y^2}{9}=1$
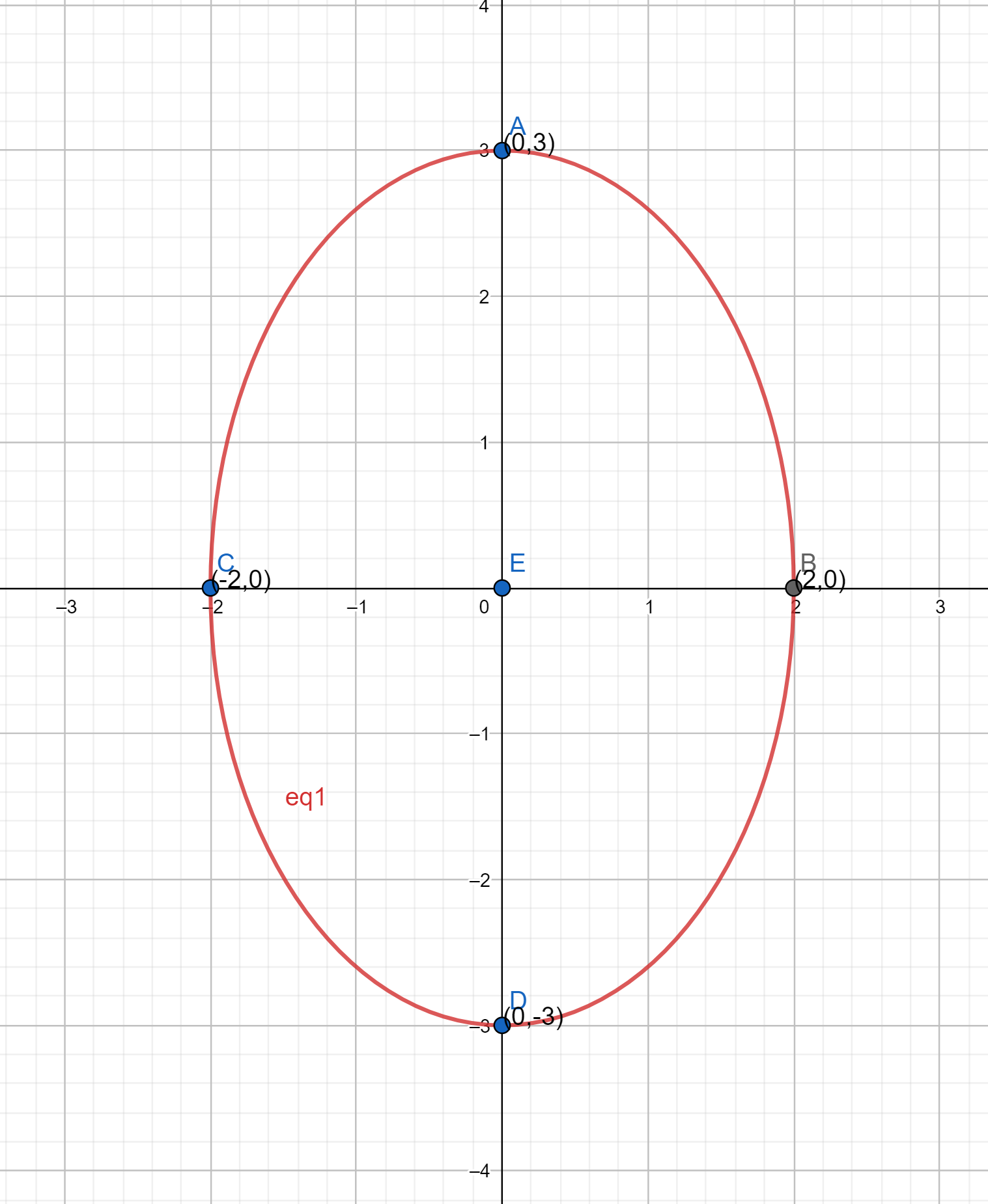
The area will be 4 times the area of EAB.
Therefore, Area of EAB $= \int_0^2 y\ dx$
$= \int^2_{0}3\sqrt{1-\frac{x^2}{4}} dx$
$= \frac{3}{2}\int^2_{0}\sqrt{4-x^2} dx$
$= \frac{3}{2}\left [ \frac{x}{2}\sqrt4-x^2 +\frac{4}{2}\sin^{-1}\frac{x}{2} \right ]^2_{0}$
$= \frac{3}{2}\left [ \frac{2\pi}{2} \right ]$
$= \frac{3\pi}{2}$
Therefore the area bounded by the ellipse will be $= 4\times \frac{3\pi}{2} = 6\pi$ units.
Question 3: Choose the correct answer in the following
$\small (A)\hspace{1mm}\pi$
$\small (B)\hspace{1mm}\frac{\pi}{2}$
$\small (C)\hspace{1mm}\frac{\pi}{3}$
$\small (D)\hspace{1mm}\frac{\pi}{4}$
Answer:
The area bounded by circle C(0,0,4) and the line x=2 is
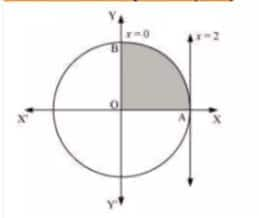
The required area = area of OAB
$\int_0^2 y\,dx = \int_0^2 \sqrt{4 - x^2}\,dx$
$= \left[ \frac{x}{2} \sqrt{4 - x^2} + \frac{4}{2} \sin^{-1} \frac{x}{2} \right]_0^2$
$= 2 \cdot \frac{\pi}{2}$
$= \pi$
Hence, The correct answer is $\pi$
Question 4: Choose the correct answer in the following.
(A) $\small 2$
(B) $\small \frac{9}{4}$
(C) $\small \frac{9}{3}$
(D) $\small \frac{9}{2}$
Answer:
The area bounded by the curve $y^2=4x$ and y =3
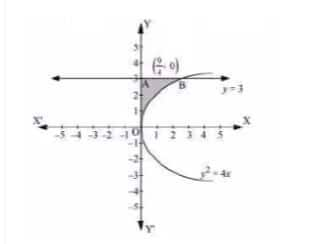
The required area = OAB
$= \int_0^3 x\,dy$
$= \int_0^3 \frac{y^2}{4}\,dy$
$= \frac{1}{4} \left[ \frac{y^3}{3} \right]_0^3$
$= \frac{9}{4}$
Hence, The correct answer is $\small \frac{9}{4}$
Also Read,
Topics covered in Chapter 8, Application of Integrals: Exercise 8.1
The main topic covered in class 12 maths chapter 8 of Application of Integrals, exercise 8.1 is:
Area under a curve: The exercise starts with calculating the area under the curve $y=f(x)$, between two points on the X axis, as $x=a$ and $x=b$. The area can be found using definite integrals as: $A=\int_a^b f(x) d x$.
Also Read,
NCERT Solutions Subject Wise
Below are some useful links for subject-wise NCERT solutions for class 12.
- NCERT solutions class 12 chemistry
- NCERT solutions for class 12 physics
- NCERT solutions for class 12 biology
- NCERT solutions for class 12 mathematics
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBookCBSE Class 12th Syllabus: Subjects & Chapters
Select your preferred subject to view the chapters
NCERT Exemplar Solutions Subject Wise
Here are some links to subject-wise solutions for the NCERT exemplar class 12.
Frequently Asked Questions (FAQs)
Q: How many questions are there in exercise 8.1 Class 12 Maths ?
A:
13 questions are in total in exercise 8.1 Class 12 Maths.
Q: Which applications are mentioned in this exercise ?
A:
Mainly area under the curve is discussed in this exercise.
Q: Is this chapter very important for Board exams ?
A:
This is very important for boards as well as other subjects like Physics also.
Q: Is it more difficult than the previous chapter ?
A:
No, it is less difficult than Chapter 7 Integrals.
Q: What are some other topics discussed in this Chapter ?
A:
Maily area and at higher level volume etc. are discussed in this.
Q: How many exercises are there in this Chapter ?
A:
Total 3 exercises are there including miscellaneous exercise.
Articles
Related Stories
|
Upcoming School Exams
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 12th
On Question asked by student community
Have a question related to CBSE Class 12th ?
Yes, you can switch from Science in Karnataka State Board to Commerce in CBSE for 12th. You will need a Transfer Certificate from your current school and meet the CBSE school’s admission requirements. Since you haven’t studied Commerce subjects like Accountancy, Economics, and Business Studies, you may need to catch up before or during 12th. Not all CBSE schools accept direct admission to 12th from another board, so some may ask you to join Class 11 first. Make sure to check the school’s rules and plan your subject preparation.
Hello
For the 12th CBSE Hindi Medium board exam, important questions usually come from core chapters like “Madhushala”, “Jhansi ki Rani”, and “Bharat ki Khoj”.
Questions often include essay writing, letter writing, and comprehension passages. Grammar topics like Tenses, Voice Change, and Direct-Indirect Speech are frequently asked.
Students should practice poetry questions on themes and meanings. Important questions also cover summary writing and translation from Hindi to English or vice versa.
Previous years’ question papers help identify commonly asked questions.
Focus on writing practice to improve handwriting and presentation. Time management during exams is key to answering all questions effectively.
Hello,
If you want to improve the Class 12 PCM results, you can appear in the improvement exam. This exam will help you to retake one or more subjects to achieve a better score. You should check the official website for details and the deadline of this exam.
I hope it will clear your query!!
For the 2025-2026 academic session, the CBSE plans to conduct board exams from 17 February 2026 to 20 May 2026.
You can download it in pdf form from below link
all the best for your exam!!
Hii neeraj!
You can check CBSE class 12th registration number in:
- Your class 12th board exam admit card. Please do check admit card for registration number, it must be there.
- You can also check the registration number in your class 12th marksheet in case you have got it.
- Alternatively you can also visit your school and ask for the same in the administration office they may tell you the registration number.
Hope it helps!
Popular CBSE Class 12th Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
CBSE Class 12th Notifications
Never miss an CBSE Class 12th update
Get timely CBSE Class 12th updates directly to your inbox. Stay informed!