Three Dimensional Geometry Class 12th Notes - Free NCERT Class 12 Maths Chapter 11 Notes - Download PDF

NCERT Notes for Class 12 Chapter 11 Three-Dimensional Geometry: Free PDF Download

Use the link below to download the PDF version of Three-Dimensional Geometry NCERT Notes for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Notes for Class 12 Chapter 11 Three-Dimensional Geometry

Three-dimensional geometry deals with the study of points, lines, and planes in space, helping us understand the position and orientation of objects in the real world.

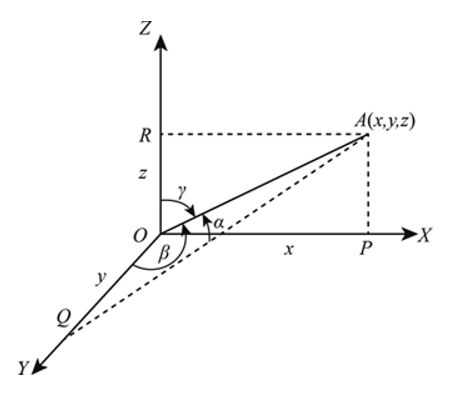
A line OA makes angles α,β,γ with the x,y, and z axes, respectively. Then cosα, cosβ, and cosγ are called direction cosines.

l = cosα, m = cosβ, n = cosγ

$\begin{aligned} & l^2+m^2+n^2=1 \\ & \cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1\end{aligned}$

Note: Direction cosines are always unique.

Direction ratios:

The values that are proportional to directional cosines are called direction ratios.
$\mathrm{a}, \mathrm{b}, \mathrm{c}$ are ratios, then $\frac{l}{a}=\frac{m}{b}=\frac{n}{c}$
Direction cosines of ratios a,b,c :
$\begin{aligned} & l= \pm \frac{a}{\sqrt{a^2+b^2+c^2}} \\ & m= \pm \frac{b}{\sqrt{a^2+b^2+c^2}} \\ & n= \pm \frac{c}{\sqrt{a^2+b^2+c^2}}\end{aligned}$

Direction cosines pass through two points:

$P\left(x_1, y_1, z_1\right)$ and $\mathrm{Q}\left(x_2, y_2, z_2\right)$

$\cos \alpha=\frac{x_2-x_1}{O A}, \cos \beta=\frac{y_2-y_1}{O A}, \cos \gamma=\frac{z_2-z_1}{O A}$

Direction cosines: $\frac{x_2-x_1}{O A}, \frac{y_2-y_1}{O A}, \frac{z_2-z_1}{O A}$

Direction ratios: $x_2-x_1, y_2-y_1, z_2-z_1$

NOTE: Directions ratios need not be unique

Equation of a Straight Line:

Equation of a Line passing through the Point and parallel to vector b

$\vec{r}=\vec{a}+\lambda \vec{b}$

where, $\vec{a}$ is a position vector. $\vec{b}$ is a vector that is parallel to the line

Cartesian form:

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}$

Where, $\left(x_1, y_1, z_1\right)$ be the point that line passes through and $\mathrm{a}, \mathrm{b}, \mathrm{c}$ are the direction ratios.

l,m,n are the direction cosines, then the equation is:

$\frac{x-x_1}{l}=\frac{y-y_1}{m}=\frac{z-z_1}{n}$

Equation of a line that passes through 2 points:

Points are : $\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)$

$\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})$

$\vec{a}, \vec{b}$ are a position vectors.

Cartesian form of two points:

Points are : $\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)$

$\frac{x-x_1}{x_1-x_2}=\frac{y-y_1}{y_1-y_2}=\frac{z-z_1}{z_1-z_2}$

Vector equations of 2 lines:

$\overrightarrow{r_1}=\overrightarrow{a_1}+\lambda\left(\overrightarrow{b_1}-\overrightarrow{a_1}\right)$ and $\overrightarrow{r_2}=\overrightarrow{a_2}+\lambda\left(\overrightarrow{b_2}-\overrightarrow{a_2}\right)$

The angle between 2 lines:

$\cos \theta=\frac{b_1 \cdot b_2}{\left|b_1\right| \cdot\left|b_2\right|}$

Cartesian form: Let be an angle between the lines below:

$\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}$ and $\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}$

Then,

$\begin{aligned} & \cos \theta=\left|\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2{ }^2+b_2{ }^2+c_2^2}}\right| \\ & \sin \theta=\sqrt{1-\cos ^2 \theta} \\ & \sin \theta=\frac{\sqrt{\left(a_1 b_2-a_2 b_1\right)^2+\left(b_1 c_2-b_2 c_1\right)^2+\left(c_1 a_2-c_2 a_1\right)^2}}{\sqrt{a_1^2+b_1^2+c_1^2} \sqrt{a_2^2+b_2^2+c_2^2}}\end{aligned}$

Direction cosines with angles are:

$\begin{aligned} & \cos \theta=l_1 l_2+m_1 m_2+n_1 n_2 \\ & \sin \theta=\sqrt{\left(m_1 n_2-m_2 n_1\right)^2+\left(n_1 l_2-n_2 l_1\right)^2+\left(l_1 m_2-l_2 m_1\right)^2}\end{aligned}$

Few conditions:

When lines are perpendicular,$\theta=90^{\circ}$

Then Cartesian form:

$\begin{aligned} & a_1 a_2+b_1 b_2+c_1 c_2=0 \\ & l_1 l_2+m_1 m_2+n_1 n_2=0\end{aligned}$

When lines are parallel $\theta=0^{\circ}$.

Then Cartesian form:

$\begin{aligned} & \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2} \\ & \frac{l_1}{l_2}=\frac{m_1}{m_2}=\frac{n_1}{n_2}\end{aligned}$

Shortest path:

Vector equations of 2 lines:

$\overrightarrow{r_1}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1}$ and $\overrightarrow{r_2}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}$

Shortest distance

$d=\left|\frac{\left(b_1 \times b_2\right) \cdot\left(a_2 \times a_1\right)}{\left(b_1 \times b_2\right)}\right|$

where $\overrightarrow{a_1}, \overrightarrow{a_2}$ are position vectors and $\overrightarrow{b_1}, \overrightarrow{b_2}$ are vectors in the direction of a line.

Cartesian form for two lines:

$\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}$ and $\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}$

Cartesian form :

Shortest distance between the lines:

$\begin{aligned} & l_1: \frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1} \\ & l_2: \frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}\end{aligned}$

$\left|\frac{\left|\begin{array}{ccc}x_2-x_1 & y_2-y_1 & z_2-z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2\end{array}\right|}{\sqrt{\left(b_1 c_2-b_2 c_1\right)^2+\left(c_1 a_2-c_2 a_1\right)^2+\left(a_1 b_2-a_2 b_1\right)^2} \mid}\right|$

Distance between two Parallel Lines:

Lines are said to be coplanar when they are parallel.

Vector equations of 2 lines:

$\overrightarrow{r_1}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1}$ and $\overrightarrow{r_2}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}$

Distance between two Parallel Lines:

$\left|\frac{\left(b_1\right) \times\left(a_2-a_1\right)}{\left|b_2\right|}\right|$

Note: If lines are parallel, they always have the same direction ratios.

Distance between two points:$P\left(x_1, y_1, z_1\right)$ and $\mathrm{Q}\left(x_2, y_2, z_2\right)$

$|P Q|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}$

The midpoint of two points: $P\left(x_1, y_1, z_1\right)$ and $\mathrm{Q}\left(x_2, y_2, z_2\right)$

$P Q=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)$

PLANE:

The plane is found unique, only if it satisfies any one of the following:

• If the normal form and distance from the origin are given
• pass-through point and perpendicular
• passes through non-collinear points

Equation of a plane in normal form:

$\vec{r} \cdot \vec{n}=d$

Cartesian form: one equation of the plane is ax + by + cz = d, and another equation of the plane is lx + my + nz = p

Formula: Foot of perpendicular (ld, md, nd).

Equation of a plane perpendicular to a vector and passing through a point:

Vector equation: $(\vec{r}-\vec{a}) \cdot \vec{n}=0$

Cartesian form: Equation of a plane that passes through the point $\left(x_1, y_1, z_1\right)$

$a\left(x-x_1\right)+b\left(y-y_1\right)+c\left(z-z_1\right)=0$

Equation of a plane passing through non-collinear points:

Vector form: $(\overrightarrow{r-a}) \cdot\{(\overrightarrow{b-a}) \times(\overrightarrow{c-} \vec{a})\}=0$

Cartesian form: $\left(x_1, y_1, z_1\right),\left(x_2, y_2, z_2\right)$ and $\left(x_3, y_3, z_3\right)$ are non-collinear points

Equation: $\left|\begin{array}{ccc}x-x_1 & y-y_1 & z-z_1 \\ x_2-x_1 & y_2-y_1 & z_2-z_1 \\ x_3-x_1 & y_3-y_1 & z_3-z_1\end{array}\right|=0$

If they are collinear: $\left|\begin{array}{lll}x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3\end{array}\right|=0$

Intercept Form:

Let a, b, and c be the x-intercept, y-intercept, and z-intercept, respectively, then

Equation of intercept: xa + by + zc = 1

Equation of Plane Passing through the intersection of two Planes: The equation of the planes is

$\overrightarrow{r_1} \cdot \overrightarrow{n_1}=d_1$ and $\overrightarrow{r_2} \cdot \overrightarrow{n_2}=d_2$

Equation of the plane passing through the intersection :

$r\left(n_1+\lambda n_2\right)=d_1+\lambda d_2$

Cartesian form: equation of planes are $a_1 x+b_1 y+c_1 z=d_1$ and $a_2 x+b_2 y+c_2 z=d_2$

Equation of the plane passing through the intersection :

$a_1 x+b_1 y+c_1 z-d_1+\lambda\left(a_2 x+b_2 y+c_2 z-d_2\right)=0$

Coplanarity:

Lines $: \overrightarrow{r_1}=\overrightarrow{a_1}+\lambda \overrightarrow{b_1}$ and $\overrightarrow{r_2}=\overrightarrow{a_2}+\mu \overrightarrow{b_2}$ are coplanar then Vectorform : $\left(\overrightarrow{a_1}-\overrightarrow{a_2}\right) \cdot\left(\overrightarrow{b_1} \times \overrightarrow{b_2}\right)=0$

Cartesian form:

For Two lines

$\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}$ and $\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}$ are coplanar then

$\left|\begin{array}{ccc}x_2-x_1 & y_2-y_1 & z_2-z_1 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2\end{array}\right|=0$

The angle between Two Planes:

θ is the angle between two planes.

$n_1, n_2$ are normals, the angle between $\overrightarrow{r_1} \cdot \overrightarrow{n_1}=d_1$ and $\overrightarrow{r_2} \cdot \overrightarrow{n_2}=d_2$

$\cos \theta=\left|\frac{n_1 \cdot n_2}{\left|n_1\right| \cdot\left|n_2\right|}\right|$

Cartesian form: planes are $a_1 x+b_1 y+c_1 z=d_1$ and $a_2 x+b_2 y+c_2 z=d_2$,

$\cos \theta=\frac{a_1 a_2+b_1 b_2+c_1 c_2}{\sqrt{a_1{ }^2+b_1^2+c_1{ }^2} \sqrt{a_2{ }^2+b_2{ }^2+c_2{ }^2}}$

Angle Between Line and Plane:

Vector form: The equation of a line is $\vec{r}=(\vec{a}+\lambda \vec{b})$

angle θ between the line and the normal to the plane is

$\cos \theta=\frac{\overrightarrow{b \cdot n}}{|\vec{b} \cdot| \vec{n} \mid}$

Cartesian form: a, b, and c are direction ratios, and lx + my + nz + d = 0 is the equation of the plane.

$\sin \theta=\frac{a l+b m+c n}{\sqrt{a^2+b^2+c^2} \sqrt{l^2+m^2+n^2}}$

Three-Dimensional Geometry: Previous Year Questions and Answers

Given below are some previous year question answers of various examinations from the NCERT class 12 chapter 11, Three Dimensional Geometry:

Question 1: The plane 2x - 3y + 6z - 11 = 0 makes an angle $\sin^{-1}(\alpha)$ with the x-axis. The value of α is:

Solution:
Given the equation of the plane is 2x - 3y + 6z - 11 = 0.

$\vec{n}=2 \hat{i}-3 \hat{j}+6 \hat{k}$
Also, the x -axis has the direction vector $\vec{b}=\hat{i}$
Also, we know that the angle $\varphi$ between the line with direction vector b and the plane having the normal vector n is:

$
\begin{aligned}
& \sin \varphi=\left|\frac{\vec{b} \cdot \vec{n}}{|\vec{b}| \cdot|\vec{n}|}\right| \\
& \Rightarrow \sin \varphi=\left|\frac{1(2)+0(-3)+0(6)}{\sqrt{2^2+3^2+6^2} \sqrt{1^2+0^2+0^2}}\right| \\
& \Rightarrow \sin \varphi=\left|\frac{2}{\sqrt{49}}\right|=\frac{2}{7} \\
& \Rightarrow \varphi=\sin ^{-1}\left(\frac{2}{7}\right) \\
& \text { On comparing, we find } \alpha=\frac{2}{7} \text { }
\end{aligned}
$

Hence, the correct answer is $\frac{2}{7}$.

Question 2: The locus represented by xy + yz = 0 is:

Solution:
Given, xy + yz = 0

⇒ x (y + z) = 0

⇒ x = 0 and y + z = 0

Clearly, the above equations are the equations of planes [of the form ax + by + cz + d = 0]

Also, $x=0$ has the normal vector $\hat{i}$
And $\mathrm{y}+\mathrm{z}=0$ has the normal vector $\hat{j}+\hat{k}$
And the dot product of these two is

$\begin{aligned}
& \hat{i}(\hat{j}+\hat{k})=\hat{i} \cdot \hat{j}+\hat{i} \cdot \hat{k} =0
\end{aligned}$

Hence, the correct answer is 'A pair of perpendicular planes'.

Question 3: The reflection of the point (α, β, γ) in the xy-plane is:

Solution:
The equation of the XY plane is $\mathrm{Z}=0$
Given point ( $a, \beta$, $y$ ); if we draw a perpendicular from this point in the $X Y$ plane, the coordinates of the plane will be
$(\alpha, \beta, 0)$.
Let the reflection be ( $x, y, z$ )
So, $\alpha=\frac{\alpha+x}{2}$

$\begin{aligned}
& \Rightarrow x=a \\
& \beta=\frac{\beta+y}{2} \\
& \Rightarrow y=\beta \\
& 0=\frac{\gamma+z}{2} \\
& \Rightarrow z=-\gamma
\end{aligned}$

Hence, the correct answer is $(α, β, -γ)$.

NCERT Class 12 Notes Chapter Wise

All the links of chapter-wise notes for NCERT class 12 maths are given below

Subject Wise NCERT Exemplar Solutions

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better clarity of the concepts.

• NCERT Exemplar Class 12 Solutions

• NCERT Exemplar Class 12 Maths

• NCERT Exemplar Class 12 Physics

• NCERT Exemplar Class 12 Chemistry

• NCERT Exemplar Class 12 Biology

Subject Wise NCERT Solutions

Students can also check these well-structured subject-wise solutions.

• NCERT Solutions for Class 12 Mathematics

• NCERT Solutions for Class 12 Chemistry

• NCERT Solutions for Class 12 Physics

• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus

Students should always analyse the latest CBSE syllabus before making a study routine. The following links will help them check the syllabus. Also, give them access to more reference books.

• NCERT Book for Class 12
• NCERT Syllabus for Class 12