Application of Integrals 12th Notes - Free NCERT Class 12 Maths Chapter 8 Notes - Download PDF

NCERT Notes for Class 12 Chapter 8 Application of Integrals: Free PDF Download

Students who wish to access the NCERT Notes for class 12, chapter 8, Application of Integrals, can click on the link below to download the entire solution in PDF.

Download PDF

NCERT Notes for Class 12 Chapter 8: Application of Integrals

Application of integrals is about integrating and finding areas under curves. Integrating is the addition or summation of all the points.

General equation of area under curves:

$y=f(x)$

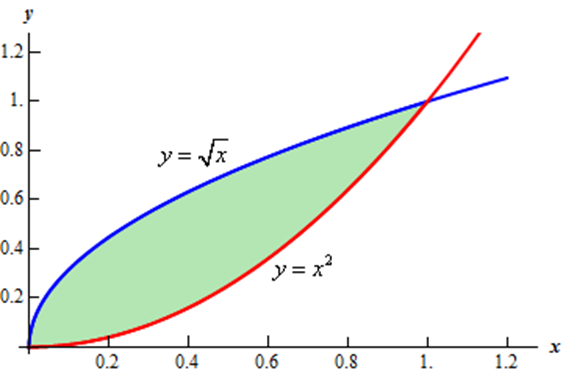
Area under simple curves:
The area under the curve is $y=f(x)$ with coordinates $x=a$ and $ x=b$.

Graph for Area Under Curves:

According to the class 12 Applications of Integrals notes, the graph for the area under the curve is:

Now, these are steps to find the integral of the function:

Step 1: Write down the equation

A = y = f(x)

Here, A denotes area

Step 2: Take the integration on both sides.

$\int_a^b A=\int_a^b y d x=\int_a^b f(x) d x$

Step 3: Find the integration

Step 4: Apply the limits and solve the equation.

Similarly, if it is for x terms, then the equation is:

$x=g(y)$ with coordinates $y=a$ and $y=b$.

Area of the above equation:

$\int_a^b A=\int_a^b x d y=\int_a^b g(y) d y$

Meanwhile, when we get an area as positive after solving the equation, then we have no issues.

But if we get an area negative, then as the area doesn’t exist in negative value so we take its absolute value, which is nothing but,
$\left|\int_a^b f(x) d x\right|$

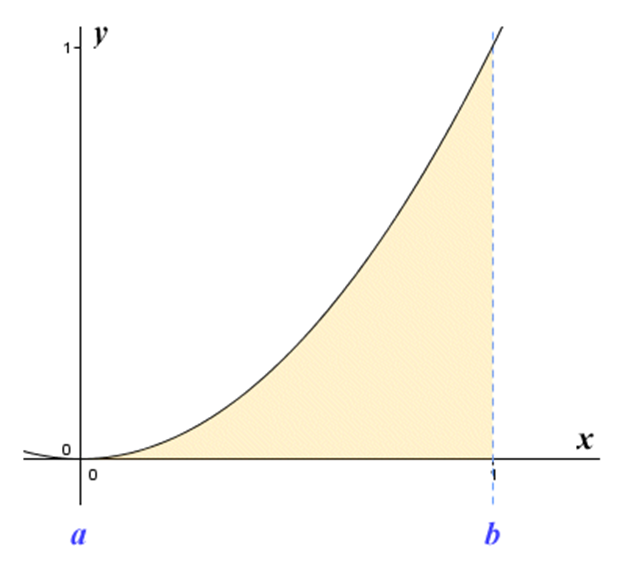
Finding the area of the region bounded by a curve and a line:

It is the same as finding an area under the curves.

The only difference is that we find the area of the region that is only enclosed by a line and a circle.

Graph for Curve Bounded by Line:

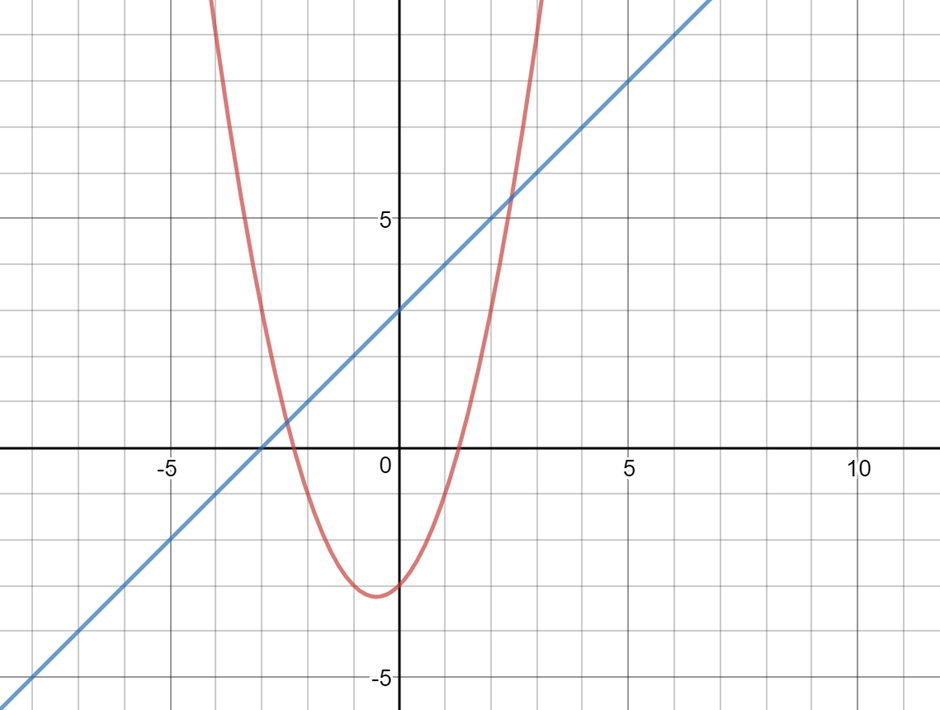
Area between two curves:

Here, we have two curves:

(a) $y=f(x)$

(b) $y=g(x)$, where $f(x)>g(x)$ in the interval [a, b].

Formulae for Area Under Two Curves:

if $y=f(x)$ and $y=g(x)$

(a) when $f(x)>g(x)$ in interval [a, b],

$A=\int_a^b(f(x)-g(x)) d x$

(b) when $f(x) > g(x)$ in [a, c] and $f(x) < g(x)$ in [c, b],

$A=\int_a^c(f(x)-g(x)) d x+\int_c^b(g(x)-f(x)) d x$

Graph Between Two Curves:

In the NCERT notes for Class 12 Maths chapter 8, the graph between two curves is given as:

Application of Integrals: Previous Year Question and Answer

Question 1:
The area (in sq. units) of the part of the circle $x^2+y^2=36$, which is outside the parabola $y^2=9 x$, is:

Solution:
The curves intersect at points $(3, \pm 3 \sqrt{3})$

Required area
$
\begin{aligned}
& =\pi r^2-2\left[\int_0^3 \sqrt{9 x} d x+\int_3^6 \sqrt{36-x^2} d x\right] \\
& =36 \pi-12 \sqrt{3}-2\left|\frac{x}{2} \sqrt{36-x^2}+18 \sin ^{-1}\left(\frac{x}{6}\right)\right|_3^6 \\
& =36 p-12 \sqrt{3}-2\left(9 \pi-\left(\frac{9 \sqrt{3}}{2}+3 \pi\right)\right)\\&=24 \pi-3 \sqrt{3}
\end{aligned}
$

Hence, the correct answer is $24 \pi-3 \sqrt{3}$.

Question 2:
The area bounded by $y=2-|2-x|$ and $y=\frac{3}{|x|} y=\frac{3}{|x|}$ is:

Solution:

As we have learned

Area between two curves:
If we have two functions that intersect each other. First, find the point of intersection.
Then integrate to find the area.
$\int_o^a[f(x)-9(x)] d x$

- wherein

$\begin{aligned} & \text { Required area }\\&=\text { area of } A B D C E A-\int_{\sqrt{3}}^3\left(\frac{3}{x}\right) d x \\ & =\frac{4-3 \log 3}{2}\end{aligned}$

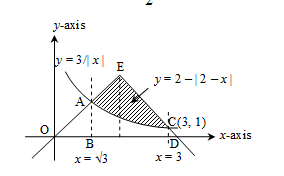
Hence, the correct answer is $\frac{4-3 \log 3}{2}$.

Question 3:
Area lying in the first quadrant and bounded by the circle $\mathrm{x}^2+\mathrm{y}^2=4$, the line $x=\sqrt{3} y$ and x -axis is:

Solution:

As we know,

Area along the y-axis:

Let $y_1=f_1(x)$ and $y_2=f_2(x)$ be two curve, then area bounded by the curves and the lines $y=a$ and $y=b$ is

$A=\int_a^b\left(x_2-x_1\right) d y$

- wherein

Required Area $=\int_0^1\left(x_2-x_1\right) d y$

$\begin{aligned} & =\int_0^1\left(\sqrt{4-y^2}-\sqrt{3} y\right) d y \\ & =\left[\frac{1}{2} y \sqrt{4-y^2}+\frac{1}{2}(4) \sin ^{-1} \frac{y}{2}-\frac{\sqrt{3} y^2}{2}\right]_0^1 \\ & =\frac{\sqrt{3}}{2}+2 \sin ^{-1}\left(\frac{1}{2}\right)-\frac{\sqrt{3}}{2}-2 \sin ^{-1} 0\\ &=\frac{\sqrt{3}}{2}+2\left(\frac{\pi}{6}\right)-\frac{\sqrt{3}}{2}\\&=\frac{\pi}{3}\end{aligned}$

Hence, the correct answer is $\frac{\pi}{3}$.

NCERT Class 12 Notes Chapter Wise

We at Careers360 compiled all the NCERT class 12 Maths Notes in one place for easy student reference. The following links will allow you to access them.

NCERT Exemplar Solutions Subject Wise

After completing the textbook exercises, students can practice the NCERT exemplars for further reference.

• NCERT Exemplar Class 12 Solutions

• NCERT Exemplar Class 12 Maths

• NCERT Exemplar Class 12 Physics

• NCERT Exemplar Class 12 Chemistry

• NCERT Exemplar Class 12 Biology

NCERT Solutions Subject Wise

These are the links to the solutions of the NCERT textbooks, subject-wise.

• NCERT Solutions for Class 12 Mathematics

• NCERT Solutions for Class 12 Chemistry

• NCERT Solutions for Class 12 Physics

• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus

It is always recommended for students to check the latest syllabus before making a study routine. Here are three links to the 2025-26 CBSE syllabus and a reference book.