Vector Algebra Class 12th Notes - Free NCERT Class 12 Maths Chapter 10 Notes - Download PDF

NCERT Notes for Class 12 Chapter 10 Vector algebra: Free PDF Download

Students who wish to access the NCERT solutions for class 12, chapter 10, Vector algebra, can click on the link below to download the entire solution in PDF.

Download PDF

NCERT Notes for Class 12 Chapter 10: Vector algebra

Vectors: Quantities that have both magnitude and direction and follow vector addition laws are called vectors.

Denoted by: $\overrightarrow{A B}$

Scalars: Quantities that have only magnitude but no direction are called scalars.

Example for Vectors and Scalars:

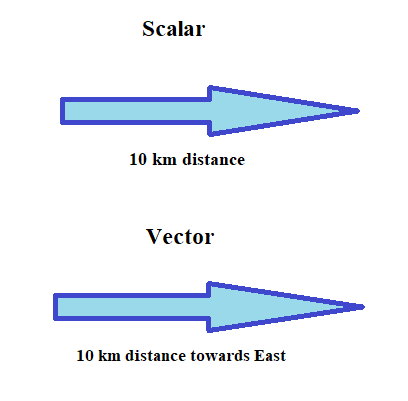
The magnitude of the vector: This shows the value of the vector and is denoted by: $|\overrightarrow{A B}|$

Representation of a Vector

A vector is represented by a directed line segment (an arrow). The endpoints of the segment are called the initial point and the terminal point of the vector. An arrow from the initial point to the terminal point indicates the direction of the vector.

Position Vector: Let $\mathrm{O}(0,0,0)$ be the origin and $\mathrm{P}(\mathrm{x}, \mathrm{y}, \mathrm{z})$ be the position vector.
Then the magnitude of a vector is denoted by: $|\overrightarrow{O P}|$
Formula: $|\overrightarrow{O P}|=\sqrt{x^2+y^2+z^2}$

Direction Cosines

Let $r$ be the position vector of a point $P(x, y, z)$. Then, the direction cosines of vector $r$ are the cosines of angles $\alpha, \beta$, and $y$ (i.e. $\cos \alpha$, $\cos \beta$, and $\cos \gamma$ ) that the vector $r$ makes with the positive direction of $X, Y$, and $Z$-axes respectively. Direction cosines are usually denoted by $I, m$, and $n$, respectively.

From the figure, note that ΔOAP is a right-angled triangle, and thus, we have

$
\cos \alpha=\frac{x}{r}(r \text { stands for }|r|)
$

Similarly, from the right angled triangles $O B P$ and $O C P$, We have,
$
\cos \beta=\frac{y}{r} \text { and } \cos \gamma=\frac{z}{r}
$

So we have the following results,
$
\begin{aligned}
& \cos \alpha=l=\frac{x}{\sqrt{x^2+y^2+z^2}}=\frac{x}{|\mathbf{r}|}=\frac{x}{r} \\
& \cos \beta=m=\frac{y}{\sqrt{x^2+y^2+z^2}}=\frac{y}{|\mathbf{r}|}=\frac{y}{r} \\
& \cos \gamma=n=\frac{z}{\sqrt{x^2+y^2+z^2}}=\frac{z}{|\mathbf{r}|}=\frac{z}{r}
\end{aligned}
$

Also,
$
\begin{aligned}
& l^2=\frac{x^2}{x^2+y^2+z^2} \\
& m^2=\frac{y^2}{x^2+y^2+z^2} \\
& n^2=\frac{z^2}{x^2+y^2+z^2}
\end{aligned}
$

Add (i), (ii) and (iii)
$
\begin{aligned}
& l^2+m^2+n^2=\frac{x^2}{x^2+y^2+z^2}+\frac{y^2}{x^2+y^2+z^2}+\frac{z^2}{x^2+y^2+z^2} \\
& \Rightarrow l^2+m^2+n^2=1 \\
& \Rightarrow \cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1
\end{aligned}
$

The coordinates of the point P may also be expressed as (lr, mr, nr).

Types of vectors

• Zero vector: A vector whose magnitude is zero is called a Zero vector. It is denoted by $|\overrightarrow{0}|$.
• Unit Vector: A vector whose magnitude is equal to one is called a Unit vector.
  $a=\frac{\vec{a}}{|\vec{a}|}$
• Coinitial Vectors: Two or more vectors are called coinitial if they have the same initial point.
  
• Collinear Vectors: If two vectors are parallel to a given line, then the vectors are called collinear.
  
• Equal Vectors: The vectors that have the same magnitude and equal direction such vectors are called Equal vectors.
  $|\vec{a}|=|\vec{b}|$
• Negative of a Vector: Vectors whose magnitude is the same but opposite in direction are called negative vectors.
  $|\overrightarrow{A B}|=|-\overrightarrow{B A}|$

Addition of vectors

Triangle law of addition

If two vectors are represented in the same direction and the resultant is represented in the opposite direction, that is called the Triangle Law of addition.

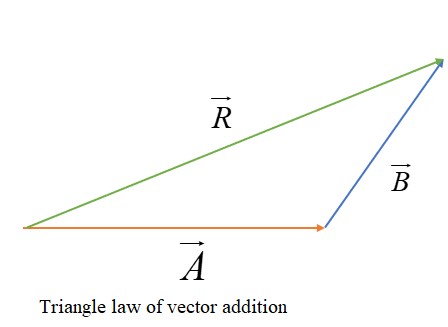
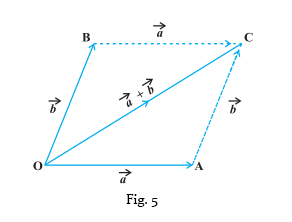
Parallelogram law of vector addition:

If two vectors are adjacent sides of the parallelogram, then the resultant vector is the diagonal of the parallelogram.
$|\overrightarrow{O A}|+|\overrightarrow{O C}|=|\overrightarrow{O B}|$

Properties of vector addition

Commutative: $\vec{a}+\vec{b}=\vec{b}+\vec{a}$
Associative: $(\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+\vec{c})$
Additive identity: $\vec{a}+\overrightarrow{0}=\vec{a}$
Additive inverse: $\vec{a}+(-\vec{a})=\overrightarrow{0}$

Multiplication of a Vector by a Scalar

Where $\vec{a}$ denotes a vector and $\lambda$ denotes a scalar.
The magnitude of $|\lambda \cdot \vec{a}|=|\lambda| \cdot|\vec{a}|$

Properties of Multiplication of Vectors

(a) $\alpha(\vec{a}+\vec{b})=\alpha \vec{a}+\alpha \vec{b}$
(b) $(\alpha+\beta) \vec{a}=\alpha \vec{a}+\beta \vec{a}$
(c) $\alpha(\beta \vec{a})=(\alpha \beta) \vec{a}$

Components of Vectors

Let the position vector be $|\overrightarrow{O P}|=\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ is a component of the vector.

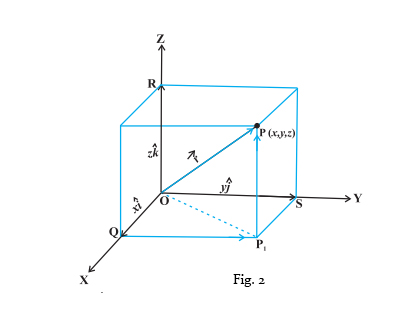
Two Dimensions:
$
\begin{aligned}
& \overrightarrow{O P}=x \hat{i}+y \hat{j} \\
& ⇒|\overrightarrow{O P}|=\sqrt{x^2+y^2}
\end{aligned}
$

Three Dimension:
$\overrightarrow{OP}= x\hat{i}+y\hat{j}+z\hat{k}$
$⇒ \overrightarrow{OP}=\sqrt{x^2+y^2+z^2}$

Vectors joining two Points

$P_1\left(x_1, y_1, z_1\right)$ and $\mathrm{P}_2\left(x_2, y_2, z_2\right)$ are any points on the axis.
Vector joining $P_1$ and $\mathrm{P}_2$ is given below:
$
\begin{aligned}
& \overrightarrow{P_1 P_2}=\left(x_2-x_1\right) \hat{i}+\left(y_2-y_1\right) \hat{j}+\left(z_2-z_1\right) \hat{k} \\
&⇒ \left|\overrightarrow{P_1 P_2}\right|=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}
\end{aligned}
$

Section Formula: $\overrightarrow{O P}$ be a position vector and line segment $A B$
- Divided internally in m:n ratio, then the formula is $\overrightarrow{O P}=\frac{m \vec{b}+n \vec{a}}{m+n}$
- Divided externally in the m:n ratio, the formula is $\overrightarrow{O P}=\frac{m \vec{b}-n \vec{a}}{m-n}$

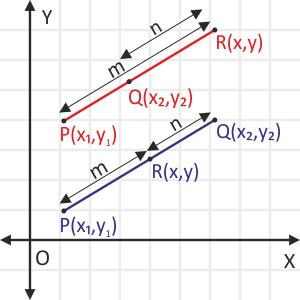
Midpoints of vectors: $\overrightarrow{O P}=\frac{\vec{a}+\vec{b}}{2}$

Dot (scalar) Product

If $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$ are two non-zero vectors, then their scalar product (or dot product) is denoted by $\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}$ and is defined as

Observations:

1. $\quad \vec{a} \cdot \vec{b}$ is a real number.
2. $\quad \vec{a} \cdot \vec{b}$ is positive if $\theta$ is acute.
3. $\quad \vec{a} \cdot \vec{b}$ is negative if $\theta$ is obtuse.
4. $\vec{a} \cdot \vec{b}$ is zero if $\theta$ is $90^{\circ}$.
5. $\quad \vec{a} \cdot \vec{b} \leq|\vec{a}||\vec{b}|$

For any two non-zero vectors $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$, then $\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}=0$ if and only if $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$ perpendicular to each other. i.e.
$
\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}=0 \Leftrightarrow \overrightarrow{\mathbf{a}} \perp \overrightarrow{\mathbf{b}}
$

As $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ are mutually perpendicular unit vectors along the coordinate axes, therefore,
$
\hat{\mathbf{i}} \cdot \hat{\mathbf{j}}=\hat{\mathbf{j}} \cdot \hat{\mathbf{i}}=0, \hat{\mathbf{j}} \cdot \hat{\mathbf{k}}=\hat{\mathbf{k}} \cdot \hat{\mathbf{j}}=0 ; \hat{\mathbf{k}} \cdot \hat{\mathbf{i}}=\hat{\mathbf{i}} \cdot \hat{\mathbf{k}}=0
$

If $\theta=0$, then $\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}=|\vec{a}||\vec{b}|$
In particular, $\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{a}}=|\overrightarrow{\mathbf{a}}|^2$
As $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ are unit vectors along the coordinate axes, therefore
$
\hat{\mathbf{i}} \cdot \hat{\mathbf{i}}=|\hat{\mathbf{i}}|^2=1, \hat{\mathbf{j}} \cdot \hat{\mathbf{j}}=|\hat{\mathbf{j}}|^2=1 \text { and } \hat{\mathbf{k}} \cdot \hat{\mathbf{k}}=|\hat{\mathbf{k}}|^2=1
$

Properties of Dot (Scalar) Product

1. $\quad \overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}}=\overrightarrow{\mathbf{b}} \cdot \overrightarrow{\mathbf{a}} \quad$ ( commutative )
2. $\overrightarrow{\mathbf{a}} \cdot(\overrightarrow{\mathbf{b}}+\overrightarrow{\mathbf{c}})=\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{c}}+\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{c}} \quad$ (distributive)
3. $\quad(m \overrightarrow{\mathbf{a}}) \cdot \overrightarrow{\mathbf{b}}=m(\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}})=\overrightarrow{\mathbf{a}} \cdot(m \overrightarrow{\mathbf{b}}) ;$ where $m$ is a scalar and $\vec{a}, \vec{b}$ are any two vectors
4. $\quad(l \overrightarrow{\mathbf{a}}) \cdot(m \overrightarrow{\mathbf{b}})=\operatorname{lm}(\overrightarrow{\mathbf{a}} \cdot \overrightarrow{\mathbf{b}})$; where $l$ and $m$ are scalars

For any two vectors $\overrightarrow{\mathbf{a}}$ and $\overrightarrow{\mathbf{b}}$, we have
(i)
$
\begin{aligned}
|\vec{a} \pm \vec{b}|^2 & =|\vec{a} \pm \vec{b}| \cdot|\vec{a} \pm \vec{b}| \\
& =|\vec{a}|^2+|\vec{b}|^2 \pm 2 \vec{a} \cdot \vec{b} \\
& =|\vec{a}|^2+|\vec{b}|^2 \pm 2|\vec{a}||\vec{b}| \cos \theta
\end{aligned}
$
(ii) $|\vec{a}+\vec{b}| \cdot|\vec{a}-\vec{b}|=|\vec{a}|^2-|\vec{b}|^2$
(iii) $|\vec{a}+\vec{b}|=|\vec{a}|+|\vec{b}| \Rightarrow \vec{a}$ and $\vec{b}$ are like vectors
(iv) $|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}| \Rightarrow \vec{a} \perp \vec{b}$

• If $\vec{a}=a_1 \hat{i}+a_2 \hat{j}+a_3 \hat{k}$ and $\vec{b}=b_1 \hat{i}+b_2 \hat{j}+b_3 \hat{k}$,
  then $\vec{a} \cdot \vec{b}=a_1 b_1+a_2 b_2+a_3 b_3$.
• If $\vec{a}, \vec{b}$ are non-zero, the angle between them can be given by:
  $\cos \theta=\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot|\vec{b}|}=\frac{a_1 b_1+a_2 b_2+a_3 b_3}{\sqrt{a_1^2+a_2^2+a_3^2} \cdot \sqrt{b_1^2+b_2^2+b_3^2}}$

Projection of a vector along another vector

Projection of $\vec{a}$ on $\vec{b}$ is given by: $\frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}$
Projection of $\vec{b}$ on $\vec{a}$ is given by: $\frac{\vec{a} \cdot \vec{b}}{|\vec{a}|}$
If $\theta=0,$ projection of $\overrightarrow{A B}$ will be $\overrightarrow{A B}$ only.
If $\theta=\pi,$ projection of $\overrightarrow{A B}$ will be $\overrightarrow{B A}$.
If $\theta=\frac{\pi}{2}$ or $\frac{3 \pi}{2},$ projection of $\overrightarrow{A B}$ will be zero.

Cross Product

$\theta$ is the angle between two non-parallel vectors $\vec{a}$ and $\vec{b}$, then the cross product is given by $\vec{a} \times \vec{b}$.
Formula : $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \theta$

Property of Cross Product

The cross product is defined as

$
\vec{a} \times \vec{b}=(|\vec{a}||\vec{b}| \sin \theta) \hat{n}
$
where $\hat{n}$ is the unit vector orthogonal to both $\hat{a}$ and $\hat{b}$ following the right-hand rule for direction, and $\theta$ is angle between the vectors.
$
\begin{aligned}
& \text {If } \vec{a}=\left[a_1, a_2, a_3\right] \text { and } \vec{b}=\left[b_1, b_2, b_3\right] \text { then } \\
& \vec{a} \times \vec{b}=\left[a_2 b_3-a_3 b_2, a_3 b_1-a_1 b_3, a_1 b_2-a_2 b_1\right]
\end{aligned}
$

The magnitude of the cross product vector is:
$
|\vec{a} \times \vec{b}|=|\vec{a}||\vec{b}| \sin \theta
$
which also calculates the area of the parallelogram defined by $\vec{a}$ and $\vec{b}$
The angle $\theta$, between two vectors, $\vec{a}$ and $\vec{b}$ is given by:
$
\theta=\sin ^{-1}\left(\frac{|\vec{a}| \times|\vec{b}|}{|\vec{a}| \cdot|\vec{b}|}\right)
$

For any vectors $\vec{a}, \vec{v}$ and $\vec{w}$ and scalar $\mathrm{k} \in \mathbb{R}$
$
\begin{aligned}
& \vec{u} \times \vec{v}=-(\vec{v} \times \vec{u}) \\
& \vec{u} \times(\vec{v}+\vec{w})=\vec{u} \times \vec{v}+\vec{u} \times \vec{w} \\
& (\vec{u}+\vec{v}) \times \vec{w}=\vec{u} \times \vec{w}+\vec{v} \times \vec{w}
\end{aligned}
$

If $\vec{u}$ and $\vec{v}$ are non zero, $\vec{u} \times \vec{v}=0$
if and only there is a scalar $\mathrm{m} \in \mathbb{R}$ such that $\vec{u}=m \vec{v}$
$
k(\vec{u} \times \vec{v})=(k \vec{u}) \times \vec{v}=\vec{u} \times(k \vec{v})
$

Vector algebra: Previous Year Question and Answer

Question 1:
Let $\overrightarrow{\mathrm{a}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+\hat{\mathrm{k}}$ and $\overrightarrow{\mathrm{b}}=2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}$. Let $\hat{\mathrm{c}}$ be a unit vector in the plane of the vectors $\vec{a}$ and $\vec{b}$ and be perpendicular to $\vec{a}$. Then such a vector $\hat{\mathbf{c}}$ is:

Solution:
$\begin{aligned} & \vec{c}=x \vec{a}+y \vec{b} \\ & \vec{c}=x(\hat{i}+2 \hat{j}+\hat{k})+y(2 \hat{i}+\hat{j}-\hat{k}) \\ & \vec{a} \cdot \vec{c}=(\hat{i}+2 \hat{j}+\hat{k}) \cdot(x(\hat{i}+2 \hat{j}+\hat{k})+y(2 \hat{i}+\hat{j}-\hat{k})) \\ & (\hat{i}+2 \hat{j}+\hat{k}) \cdot(x \hat{i}+2 x \hat{j}+x \hat{k})+2 y \hat{i}+y \hat{j}-y \hat{k}=0 \\ & \Rightarrow \quad(x+2 y)+2(x+9)+(x-y)=0 \\ & \Rightarrow \quad y=-2 x \\ & \therefore \quad \vec{c}=x(-3 \hat{i}+3 \hat{k}) \\ & |\vec{c}|=|x| \sqrt{9+9}=3|x| \sqrt{2} \\ & \therefore|\vec{c}|=1 \\ & 3|x| \sqrt{2}=1 \\ & |x|=\frac{1}{3 \sqrt{2}} \\ & \text { Let } x=\frac{1}{3 \sqrt{2}} \\ & \vec{c}=\frac{1}{3 \sqrt{2}}(-3 \hat{i}+3 \hat{k}) \\ & ⇒ \vec{c}=\frac{1}{\sqrt{2}}(-\hat{i}+\hat{k})\end{aligned}$

Hence, the correct answer is $\frac{1}{\sqrt{2}}(-\hat{\mathrm{i}}+\hat{\mathrm{k}})$.

Question 2:
Let $\vec{a}$ and $\vec{b}$ be the vectors of the same magnitude such that $\frac{|\vec{a}+\vec{b}|+|\vec{a}-\vec{b}|}{|\vec{a}+\vec{b}|-|\vec{a}-\vec{b}|}=\sqrt{2}+1$. Then $\frac{|\vec{a}+\vec{b}|^2}{|\vec{a}|^2}$ is:

Solution:
$
\frac{|\overline{\mathrm{a}}+\overline{\mathrm{b}}|+|\overline{\mathrm{a}}-\overline{\mathrm{b}}|}{|\overline{\mathrm{a}}+\overline{\mathrm{b}}|-|\overline{\mathrm{a}}-\overline{\mathrm{b}}|}=\sqrt{2}+1
$
Apply componendo and dividendo

$
\begin{aligned}
& \Rightarrow \frac{2|\bar{a}+\bar{b}|}{2|\bar{a}-\bar{b}|}=\frac{\sqrt{2}+2}{\sqrt{2}} \\
& \Rightarrow|\bar{a}+\bar{b}|=(1+\sqrt{2})|\bar{a}-\bar{b}| \\
& \Rightarrow|\bar{a}+\bar{b}|^2=(3+2 \sqrt{2})|\bar{a}-\bar{b}|^2 \\
& \Rightarrow 2|\bar{a}|^2+2 \bar{a} \cdot \bar{b}=(3+2 \sqrt{2})\left(2|\bar{a}|^2-2 \bar{a} \cdot \bar{b}\right) \\
& \Rightarrow 2|\bar{a}|^2(2+2 \sqrt{2})=2 \bar{a} \cdot \bar{b}(4+2 \sqrt{2}) \\
& \Rightarrow \frac{\bar{a} \cdot \bar{b}}{|\bar{a}|^2}=\frac{2+2 \sqrt{2}}{4+2 \sqrt{2}}=\frac{1}{\sqrt{2}}
\end{aligned}
$
Now

$
\begin{aligned}
& \frac{|\bar{a}+\bar{b}|^2}{|\bar{a}|^2}=1+\frac{|\bar{b}|^2}{|\bar{a}|^2}+\frac{2 \bar{a} \cdot \bar{b}}{|\bar{a}|^2} \\
& =1+1+2\left(\frac{1}{\sqrt{2}}\right)\\&=2+\sqrt{2}
\end{aligned}
$

Hence, the correct answer is $2+\sqrt{2}$.

Question 3:

Let in a $\triangle A B C$, the length of the side $A C$ be 6 , the vertex $B$ be $(1,2,3)$ and the vertices $A, C$ lie on the line $\frac{x-6}{3}=\frac{y-7}{2}=\frac{z-7}{-2}$. Then the area (in sq. units) of $\triangle A B C$ is:

Solution:

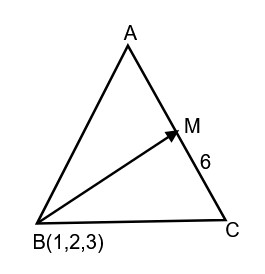
Compare the given equation with,

$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$

We get, $x_0=6,y_0=7,z_0=7,a=3,b=2,c=-2$

And write the point in parametrized form $(a\lambda+x_0,b \lambda+y_0, c \lambda+z_0)$

Let $\mathrm{M}(3 \lambda+6,2 \lambda+7,-2 \lambda+7)$
$\overrightarrow{\mathrm{BM}}=(3 \lambda+5) \hat{i}+(2 \lambda+5) \hat{j}+(-2 \lambda+4) \hat{k}$
$\overrightarrow{\mathrm{AC}} \cdot \overrightarrow{\mathrm{BM}}=0$

Since, the dot product is zero, we can calculate the value of $\lambda$,

$0=3(3 \lambda+5)+2(2 \lambda+5)-2(-2 \lambda+4)$

$9\lambda+15+4\lambda+10+4\lambda-8=0$

$17\lambda=-17$

$\lambda=-1$

Now, put the value in the $\overrightarrow{BM}$,

$\overrightarrow{\mathrm{BM}}=(3 \times (-1)+5) \hat{i}+(2 \times(- 1)+5) \hat{j}+(-2 \times (-1)+4) \hat{k}$
$\overrightarrow{\mathrm{BM}}=2 \hat{i}+3 \hat{j}+6 \hat{k}$

Let us calculate the magnitude of this vector,

$|\overrightarrow{\mathrm{BM}}|=\sqrt{(2)^2+(3)^2+(6^2)}$

$|\overrightarrow{\mathrm{BM}}|=\sqrt{4+9+36}$

$|\overrightarrow{\mathrm{BM}}|=\sqrt{49}$
$|\overrightarrow{\mathrm{BM}}|=7$

We can calculate the area by using the formula:

Area $=\frac{1}{2} \times 6 \times 7=21 \text{ sq. units}$

Hence, the correct answer is 21.

NCERT Class 12 Notes Chapter Wise

For students' preparation, Careers360 has gathered all Class 8 Maths NCERT Notes here for quick and convenient access.

NCERT Exemplar Solutions Subject-Wise

After completing the NCERT textbooks, students should practice exemplar exercises for a better understanding of the chapters and clarity. The following links will help students find exemplar exercises.

• NCERT Exemplar Class 12 Solutions

• NCERT Exemplar Class 12 Maths

• NCERT Exemplar Class 12 Physics

• NCERT Exemplar Class 12 Chemistry

• NCERT Exemplar Class 12 Biology

NCERT Solutions Subject-Wise

These are links to the solutions of other subjects, which students can check to revise and strengthen those concepts.

• NCERT Solutions for Class 12 Mathematics

• NCERT Solutions for Class 12 Chemistry

• NCERT Solutions for Class 12 Physics

• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus

Students should always check the latest NCERT syllabus before planning their study routine. Also, some reference books should be read after completing the textbook exercises. The following links will be very helpful for students for these purposes.