NCERT Class 12 Maths Chapter 1 Notes, Relations and Functions Class 12 Chapter 1 Notes

NCERT Notes for Class 12 Chapter 1 Relations and Functions: Free PDF Download

Use the link below to download the PDF version of Relations and Functions NCERT Notes for free. After that, you can view the PDF anytime you desire without internet access. It is very useful for revision and last-minute studies.

Download PDF

NCERT Notes for Class 12 Chapter 1 Relations and Functions:

Two sets, A and B, are related if there is a recognisable connection or link between the elements of sets A and B. Let ‘a’ be an element of set A and ‘b’ be an element of set B. If $(a,b)\in R$, we can say that a is related to b under the relation R. We can write as "aRb" to describe the relation.
Let a relation R be defined as $R: A → B$.
Example: If A = {1, 2, 3} and B = {a, b, c}, then R = {(1, b), (2, c), (1, a), (3, a)} being a subset of A × B, is a relation from A to B.
Here, (1, b), (2, c), (1, a), and (3, a) belong to R, so we write 1 Rb, 2Rc, 1Ra, and 3Ra.

Total Number of Relations: Let A and B be two non-empty finite sets consisting of m and n elements, respectively. Then A x B consists of mn ordered pairs. So, the total number of subsets of A x B is 2mn.

Domain: The set of all first elements of the ordered pairs in a relation R from a set A to a set B is called the domain of the relation R.
Domain of $\mathrm{R}\{\mathrm{a}:(\mathrm{a}, \mathrm{b}) \in \mathrm{R}\}$

Range: The set of all second elements in a relation R from a set A to a set B is called the range of the relation R.
Range of $R\{b:(a, b) \in R\}$

Co-domain: The whole set B is called the co-domain of the relation R.

Note: Range subset of co-domain.

Types of Relation:

Empty Relation: No element of $A$ is related to any element of $A$, i.e.,
$
\mathrm{R}=\phi \subset \mathrm{A} \times \mathrm{A}
$
Universal relation: Each element of $\operatorname{set} \mathrm{A}$ is related to every element of $\operatorname{set} \mathrm{A}$ i.e.

$
\mathrm{R}=\mathrm{A} \times \mathrm{A}
$

Note: Both empty relation and universal relation are called trivial relation.

Identity Relation: A relation R on A is called the identity relation if every element of A is related to itself only. Let A be a set. Then the relation R = {(a, a) : a belongs to A} on A is called the identity relation on A.

Reflexive Relation: A relation R on a set A is said to be reflexive if every element of A is related to itself. If $(a,a) \in R$ for every $a\in A$.

Note: Every Identity relation is reflexive, but every reflexive relation is not identity.

Symmetric Relation: if $\left(a_1, a_2\right) \in \mathrm{R} \Rightarrow\left(a_2, a_1\right) \in \mathrm{R}\ {\text {for all }} a_1, a_2 \in \mathrm{~A}$

Transitive Relation: if $\left(a_1, a_2\right) \in \mathrm{R}$ and $\left(a_2, a_3\right) \in \mathrm{R} \Rightarrow\left(a_1, a_3\right) \in \mathrm{R}$ for all $a_1, a_2, a_3 \in \mathrm{~A}$

Equivalence Relation: If a relation R is reflexive, symmetric, and transitive, then it is said to be an equivalence relation.

Types of Function:

The function is a binary relation between two sets A and B that associates each element of set A to exactly one element of set B. So, if a vertical line cuts a given graph at more than one point, then it can not be the graph of a function.

Note: Every function is a relation, but every relation is not necessarily a function.

Let a function 'f' be defined as $f: A→B$.

Set A is called the domain of the function.

Set B is called the co-domain of the function.

The set of 'f' images of all the elements of set A is known as the range of the function 'f'.

There are many types of functions we need to learn about, some of the important ones are:

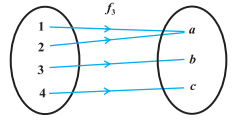
Injective function: A function $f$ is called injective if the images of distinct elements of $A$ under $f$ are distinct.
If function $f: \mathrm{A} \rightarrow \mathrm{B}$ is defined for every $a_1, a_2 \in \mathrm{~A}, f\left(a_1\right)=f\left(a_2\right)$ $\Rightarrow a_1=a_2$. Then this is one-one function.

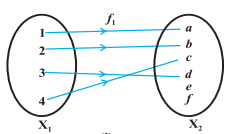
Many-one function: A function f is called many-one if the images of distinct elements of A under f can be the same.

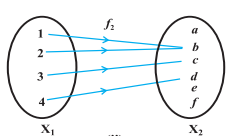
Surjective function: A function $f: X→Y$ is called Surjective if every element of Y is the image of some element of X.

Composition of Functions and Invertible Functions:

If function $f: A \rightarrow B$ and $g: B \rightarrow C$ are two functions then the composite function of two functions 'f' and 'g' is $g \circ f: A \rightarrow C$ is defined as $g \circ f(x)=g(f(x)) \forall x \in A$.

Example: If $f(x)=8 x^3$ and $g(x)=x^{\frac{1}{3}}$ than find $\mathrm{f}(\mathrm{g}(\mathrm{x}))$ and $\mathrm{g}(\mathrm{f}(\mathrm{x}))$
Solution:
The solution is as follows
$
\begin{aligned}
& \text { (ii) } f(x)=8 x^3 \text { and } g(x)=x^{\frac{1}{3}} \\
& \text { g o f }=g(f(x)) \\
& =g\left(8 x^3\right) \\
& =\left(8 x^3\right)^{\frac{1}{3}} \\
& =2 x
\end{aligned}
$

$\begin{aligned} & \text{f o g}=f(g(x)) \\ & =f\left(x^{\frac{1}{3}}\right) \\ & =8\left(\left(x^{\frac{1}{3}}\right)^3\right) \\ & =8 x\end{aligned}$

Inverse function:
If function $f: \mathrm{A} \rightarrow \mathrm{B}$ be a one-one and onto function, then there exists a unique function $g: \mathrm{B} \rightarrow \mathrm{A}$ such that
$f(x)=y \Leftrightarrow g(y)=x$ $\forall x \in A \quad \& \quad y \in B$.
The function g is the inverse of f.
$g=\mathrm{f}^{-1}: \mathrm{B} \rightarrow \mathrm{~A} .$

Example:
If the function $f(x)=4 x+3$ is defined $f: R \rightarrow R,$ then find the inverse of $f$.
Solution:

$
\begin{aligned}
& f(x)=4 x+3 \\
& y=4 x+3, y \in R \\
& \Rightarrow x=f^{-1}(y)=\frac{y-3}{4} \in R
\end{aligned}
$

Algebraic Operations on Functions:

Let two real-valued functions f & g be given with domain set A, B respectively.

(i) (f + g ) ( x) = f(x) + g(x) (domain is $A \cap B$ )

(ii) (f - g ) ( x) = f(x) - g(x) (domain is $A \cap B$ )

(iii) (f . g ) ( x) = f(x) g(x) (domain is $A \cap B$ )

(iv) $(\frac fg ) ( x) =\frac{ f(x)}{g(x)}$ (domain is $A \cap B$ - { x | g(x) = 0 } )

Binary Operations:
Binary operation * on a set A is a function $*: A \times A \rightarrow A$. Binary operation * is denoted $*(a, b)$ as $a * b$.

• Commutative property: If $a * \mathrm{~b}=\mathrm{b} * \mathrm{a}$ for every $\mathrm{a}, \mathrm{b} \in \mathrm{A},{\text {than * }}$ is commutative on A.
• Associative property: If $(a * \mathrm{~b}) * c=a *(\mathrm{~b} * \mathrm{c})$ for every $\mathrm{a}, \mathrm{b}, c \in \mathrm{~A},{\text {than }}$ * is associative on $A$.
• Identity: If an element e in set A exists such that $a * \mathrm{e}=\mathrm{a}=\mathrm{e} * \mathrm{a}, \forall \mathrm{a} \in \mathrm{A}$ then ' e ' is an identity element for * on set A.

Note: Zero is the identity for the addition operation on R but not on N, as 0 doesn't belong to N.

Relations and Functions: Previous Year Question and Answer

Given below are some previous year question answers of various examinations from the NCERT class 12 chapter 1, Relations and Functions:

Question 1: Assertion (A): Let $Z$ be the set of integers. A function $f: Z \rightarrow Z$ defined as $\mathrm{f}(x)=3 x-5, \forall x \in \mathrm{Z}$ is a bijective.
Reason (R): A function is bijective if it is both surjective and injective.
Choose the correct option from below:
(1.) Both Assertion (A) and Reason (R) are true, and the Reason (R) is the correct explanation of the Assertion (A).
(2.) Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
(3.) Assertion (A) is true, but Reason (R) is false.
(4.) Assertion (A) is false, but Reason (R) is true.

Solution:
Assertion (A):
Let $\mathbb{Z}$ be the set of integers.
A function $f: \mathbb{Z} \rightarrow \mathbb{Z}$, defined as
$f(x)=3x-5, \forall x \in \mathbb{Z}$ is a bijection.

Injectivity (One-one)
Let $f\left(x_1\right)=f\left(x_2\right)$
$\Rightarrow 3 x_1-5=3 x_2-5$
$\Rightarrow x_1=x_2$
So, $f$ is injective.

Surjectivity (Onto)
We want to see if every integer $y \in \mathbb{Z}$ has some $x \in \mathbb{Z}$ such that $f(x)=y$
Let $y=3 x-5 \Rightarrow x=\frac{y+5}{3}$
Now, for arbitrary $y \in \mathbb{Z}, \frac{y+5}{3}$ is not always an integer (e.g., if $y=1 \Rightarrow x=\frac{6}{3}=2$
but if $y=0 \Rightarrow x=\frac{5}{3} \notin \mathbb{Z}$)
So, not every integer $y$ has a pre-image $\rightarrow f$ that is not onto.
Hence, $f$ is not bijective.

Reason (R):
"A function is bijective if it is both surjective and injective."
$\rightarrow$ This is true by definition.
Therefore, Assertion (A) is false, but Reason (R) is true.

Hence, the correct answer is option (4).

Question 2: If $f: R \rightarrow R$ be given by $f(x)=\tan x$, then $f^{-1}(1)$ is:

Solution:
Here, $f(x)=\tan x$
Assume, $f(x)=y=\tan x$
Then, $\quad x=\tan ^{-1}(y)$
or, $f^{-1}(x)=\tan ^{-1}(x)$
or, $f^{-1}(1)=\tan ^{-1}(1)$
or, $f^{-1}(1)=\tan ^{-1} \tan (\frac{\pi}{4})=\frac{\pi}{4}$

Hence, the correct answer is $\frac{\pi}{4}$.

Question 3:
Let $\mathrm{f}: R \rightarrow R$ be defined by

$
f(x)= \begin{cases}2 x & \text { when } x>3 \\ x^2 & \text { when } 1<x \leq 3 \\ 3 x & \text { when } x \leq 1\end{cases}
$
The expression $(f(-1)+f(2)+f(4))$ is :

Solution:

Here, $f(-1)+f(2)+f(4)$
$=3(-1)+(2)^2+2(4)$
$=-3+4+8=9$

Hence, the correct answer is $9$.

NCERT Class 12 Notes Chapter Wise

All the links of chapter-wise notes for NCERT class 12 maths are given below:

Subject Wise NCERT Exemplar Solutions

After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better clarity of the concepts.

• NCERT Exemplar Class 12 Solutions

• NCERT Exemplar Class 12 Maths

• NCERT Exemplar Class 12 Physics

• NCERT Exemplar Class 12 Chemistry

• NCERT Exemplar Class 12 Biology

Subject Wise NCERT Solutions

Students can also check these well-structured subject-wise solutions.

• NCERT Solutions for Class 12 Mathematics

• NCERT Solutions for Class 12 Chemistry

• NCERT Solutions for Class 12 Physics

• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus

Students should always analyse the latest CBSE syllabus before making a study routine. The following links will help them check the syllabus. Also, give them access to more reference books.

• NCERT Book for Class 12
• NCERT Syllabus for Class 12