NCERT Solutions for Class 12 Maths Chapter 12 Linear Programming

Question 1: Solve the following Linear Programming Problems graphically: Maximise $Z = 3x + 4y$ Subject to the constraints $x+y\leq 4,x\geq 0,y\geq 0.$

Answer:

The region determined by constraints, $x+y\leq 4,x\geq 0,y\geq 0.$ is as follows,

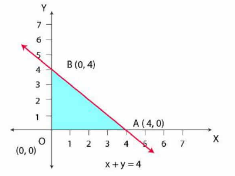
The region A0B represents the feasible region

The corner points of the feasible region are $B(4,0),C(0,0),D(0,4)$

Maximize $Z = 3x + 4y$

The value of these points at these corner points are :

The maximum value of Z is 16 at $D(0,4)$

Question 2: Solve the following Linear Programming Problems graphically: Minimise $z=-3x+4y$ Subject to . $x+2y\leq 8,3x+2y\leq 12,x\geq 0,y\geq 0.$

Answer:

The region determined by constraints, $x+2y\leq 8,3x+2y\leq 12,x\geq 0,y\geq 0.$ is as follows,

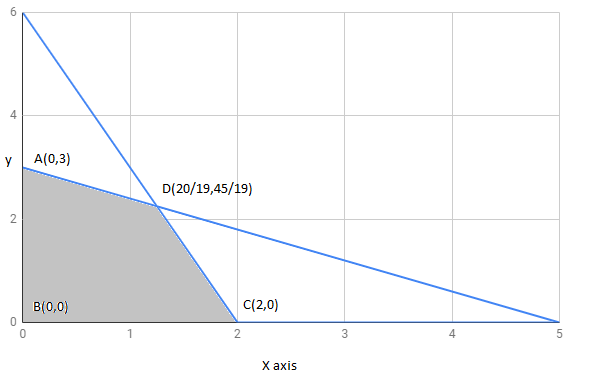
The corner points of feasible region are $A(2,3),B(4,0),C(0,0),D(0,4)$

The value of these points at these corner points are :

The minimum value of Z is -12 at $B(4,0)$

Question 3: Solve the following Linear Programming Problems graphically: Maximise $Z = 5x + 3y$ Subject to $3x + 5y \leq 15$ , $5x+2y\leq 10$ , $x\geq 0,y\geq 0$

Answer:

The region determined by constraints, $3x + 5y \leq 15$ , $5x+2y\leq 10$ , $x\geq 0,y\geq 0$ is as follows :

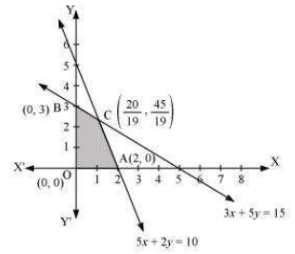
The corner points of feasible region are $A(0,3),B(0,0),C(2,0),D(\frac{20}{19},\frac{45}{19})$

The value of these points at these corner points are :

The maximum value of Z is $\frac{235}{19}$ at $D(\frac{20}{19},\frac{45}{19})$

Question 4: Solve the following Linear Programming Problems graphically: Minimise $Z = 3x + 5y$ Such that $x+3y\geq 3,x+y\geq 2,x,y\geq 0.$

Answer:

The region determined by constraints $x+3y\geq 3,x+y\geq 2,x,y\geq 0.$ is as follows,

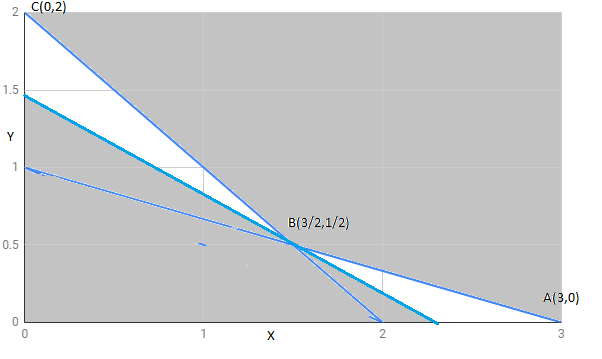
The feasible region is unbounded as shown.

The corner points of the feasible region are $A(3,0),B(\frac{3}{2},\frac{1}{2}),C(0,2)$

The value of these points at these corner points is:

The feasible region is unbounded, therefore, 7 may or may not be the minimum value of Z.

For this, we draw $3x + 5y< 7$ and check whether the resulting half plane has a point in common with the feasible region or not.

We can see that a feasible region has no common point with. $Z = 3x + 5y$

Hence, Z has a minimum value of 7 at $B(\frac{3}{2},\frac{1}{2})$

Question 5: Solve the following Linear Programming Problems graphically: Maximise $Z = 3x + 2y$ Subject to $x+2y\leq 10,3x+y\leq 15,x,y\geq 0$

Answer:

The region determined by constraints, $x+2y\leq 10,3x+y\leq 15,x,y\geq 0$ is as follows,

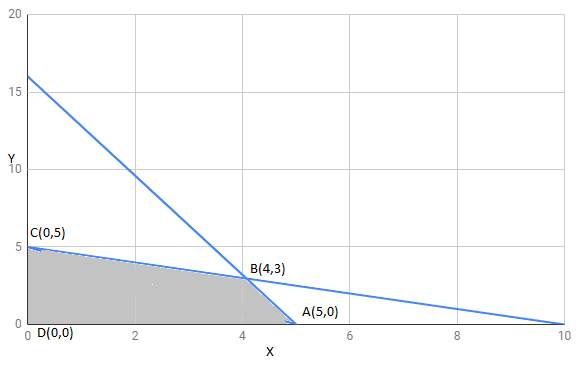
The corner points of feasible region are $A(5,0),B(4,3),C(0,5)$

The value of these points at these corner points are :

The maximum value of Z is 18 at $B(4,3)$

Question 6: Solve the following Linear Programming Problems graphically: Minimise $Z = x + 2y$ Subject to $2x+y\geq 3,x+2y\geq 6,x,y\geq 0.$

Answer:

The region determined by constraints $2x+y\geq 3,x+2y\geq 6,x,y\geq 0.$ is as follows,

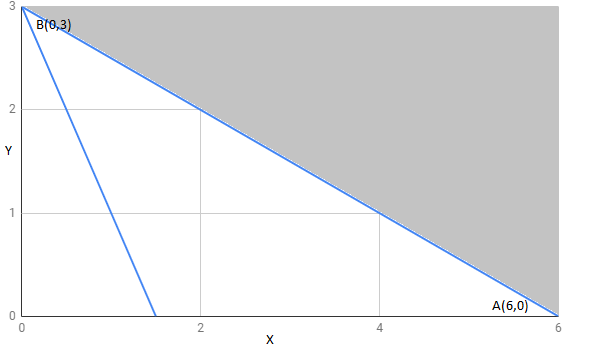
The corner points of the feasible region are $A(6,0),B(0,3)$

The value of these points at these corner points are :

The value of Z is the same at both points. $A(6,0),B(0,3)$

If we take any other point like $(2,2)$ on line $Z = x + 2y$, then Z=6.

Thus, the minimum value of Z occurs at more than 2 points.

Therefore, the value of Z is minimum at every point on the line $Z = x + 2y$.

Question 7: Solve the following Linear Programming Problems graphically: Minimise and Maximise $z=5x+10y$ Subject to $x+2y\leq 120,x+y\geq 60,x-2y\geq 0,x,y\geq 0$ Show that the minimum of Z occurs at more than two points.

Answer:

The region determined by constraints, $x+2y\leq 120,x+y\geq 60,x-2y\geq 0,x,y\geq 0$ is as follows,

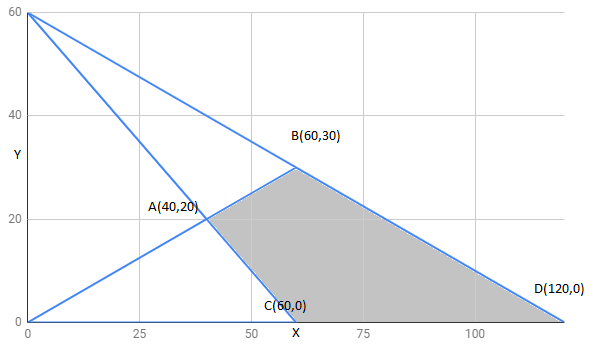
The corner points of feasible region are $A(40,20),B(60,30),C(60,0),D(120,0)$

The value of these points at these corner points are:

The minimum value of Z is 300 at $C(60,0)$ and the maximum value is 600 at all points joining line segment $B(60,30)$ and $D(120,0)$

Question 8: Solve the following Linear Programming Problems graphically: Minimise and Maximise $z=x+2y$ Subject to $x+2y\geq 100,2x-y\leq 0,2x+y\leq 200,x,y,\geq 0$ Show that the minimum of Z occurs at more than two points.

Answer:

The region determined by constraints $x+2y\geq 100,2x-y\leq 0,2x+y\leq 200,x,y,\geq 0$ is as follows,

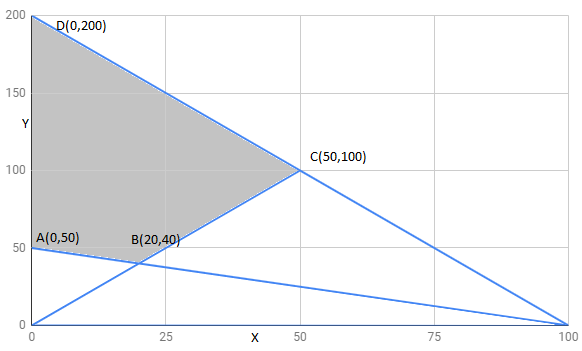
The corner points of the feasible region are $A(0,50),B(20,40),C(50,100),D(0,200)$

The value of these points at these corner points are :

The minimum value of Z is 100 at all points on the line segment joining points $A(0,50)$ and $B(20,40)$.

The maximum value of Z is 400 at $D(0,200)$.

Question 9: Solve the following Linear Programming Problems graphically: Maximise $Z = -x+2y$ Subject to the constraints: $x\geq 3,x+y\geq 5,x+2y\geq 6,y\geq 0.$ Show that the minimum of Z occurs at more than two points.

Answer:

The region determined by constraints $x\geq 3,x+y\geq 5,x+2y\geq 6,y\geq 0.$ is as follows,

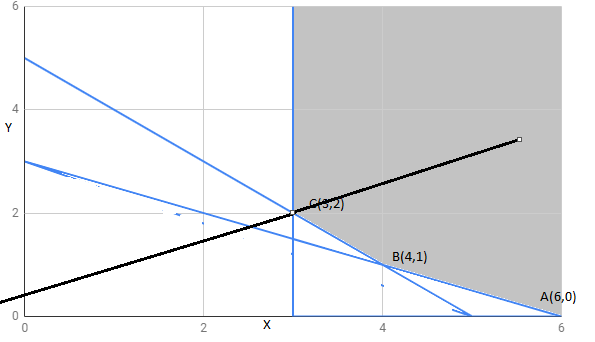
The corner points of the feasible region are $A(6,0),B(4,1),C(3,2)$

The value of these points at these corner points are :

The feasible region is unbounded, therefore, 1 may or may not be the maximum value of Z.

For this, we draw $-x+2y> 1$ and check whetherthe resulting half-plane has a point in common with a feasible region or not.

We can see the resulting feasible region has a common point with the feasible region.

Hence, Z =1 is not the maximum value; Z has no maximum value.

Question 10: Solve the following Linear Programming Problems graphically: Maximise $Z = x + y,$ Subject to $x-y\leq -1,-x+ y\leq 0,x,y,\geq 0.$. Show that the minimum of Z occurs at more than two points.

Answer:

The region determined by constraints $x-y\leq -1,-x+ y\leq 0,x,y,\geq 0.$ is as follows,

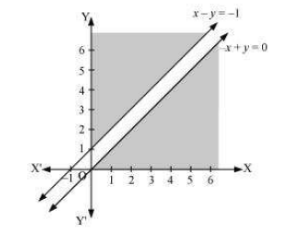
There is no feasible region, and thus, Z has no maximum value.

• Linear Programming Class 12 Exercise 12.1

Class 12 Maths NCERT Chapter 12: Extra Question

Question: In an LPP, if the objective function $z=a x+b y$ has the same maximum value on two corner points of the feasible region, then the number of points at which $z_{\max }$ occurs is:

Solution:
In an LPP, if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points gives the same maximum value. Hence, the number of points at which Zmax occurs is infinite.

Hence, the correct answer is "infinite".

Approach to Solve Questions of Linear Programming Class 12

• Determine whether the problem requires maximisation or minimisation.
• Check if variables are negative or non-negative. If they are non-negative, then they will satisfy a set of linear constraints.
• Plot all the constraints carefully on the graph paper based on their inequalities. Find and shade the feasible region—bounded or unbounded—that satisfies all constraints simultaneously.
• Shortcut tricks:

- Label all the axes and lines clearly in the graph paper to understand the representation.

- Be aware of the mistakes made during the plotting or solving of intersections.

- If the region is unbounded, the optimal value may not exist.