Linear Programming Class 12th Notes - Free NCERT Class 12 Maths Chapter 12 Notes - Download PDF
In a world of constraints, linear programming is your path to the best possible outcome. If you own a bakery and are aware that you are limited in supplies of flour and sugar, but you want to bake as many cakes and cookies as possible to maximise your profit, how do you determine what to bake? Well, this is where Linear programming comes in and examines the best possible choice under your constraints. These NCERT Notes on Linear Programming cover the following concepts: Objective Function, Decision Variables, Constraints, Feasible Region and Optimal Solution. By studying the concepts in this chapter, students will understand Linear Programming better and be able to apply the techniques for problem-solving in real-life applications. The primary objective of the Linear Programming Class 12 notes in Maths is to help students achieve optimal results when they are constrained by specific factors and limitations.
This Story also Contains
- Linear Programming Class 12 Notes Free PDF Download
- Linear Programming Class 12 Notes
- How to Use the Linear Programming Class 12 Notes Effectively?
- Linear Programming Class 12 Notes: Previous Year Question and Answer
- NCERT Class 12 Maths Notes Chapter-Wise Links

Linear Programming is not just a topic; it is a big part of our problem-solving skills in the real world, by learning how to operate under limitations. This article on NCERT Class 12 Maths Chapter 12 Notes on Linear Programming provides structured study notes for students to help them master the concepts of Linear Programming easily. Students who want to revise the key topics of Linear Programming quickly will find this article very useful. It will also boost the exam preparation of the students by many folds. Experienced Careers360 Subject Matter Experts prepared these NCERT class 12 linear programming notes to align with the latest CBSE syllabus, so students can effectively grasp the basic concepts. Check this NCERT article for complete syllabus coverage along with NCERT Books, Solutions, Syllabus, and Exemplar Problems with Solutions.
Also, read,
Linear Programming Class 12 Notes Free PDF Download
Students who wish to access these NCERT Class 12 Maths Chapter 12 Notes can click on the link below to download the entire solutions in PDF.
Linear Programming Class 12 Notes
Careers360 has prepared these NCERT Class 12 Maths Chapter 12 Notes to make your revision smoother and faster.
Linear programming is generally defined as the technique for maximising or minimising a linear function of several variables, like input or output cost.
Linear Programming Problem And Its Mathematical Formula
A Mountaineering equipment dealer deals in only two items–tents and rucksacks. He has Rs 50,000 for investment and has storage for compiling a maximum of 60 pieces. A tent is priced at Rs 2500 and a rucksack at Rs 500. He estimates that by selling one tent he can get a profit of Rs 250 and that from the. The sale of one rucksack earns a profit of Rs 75. So, how many tents and rucksacks should he buy with the money to maximise his total profit, assuming he can sell all the products he buys?
Here we can observe,
- The dealer can invest his money in buying a tent or rucksacks, or a combination thereof. Later, he would earn different ways of profits by following different investment strategies.
- There are a lot of conditions, i.e., His investment is a maximum of Rs 50,000, and he has a storage of a maximum of 60 pieces.
Let us assume that he decides to buy a tent only and no rucksacks, so he can buy 50000 ÷ 2500, i.e., 20 tents. Thus, his profit can be written as: Rs (250 × 20), i.e., Rs 5000.
Suppose he chooses to buy rucksacks only and no tent. With the capital of Rs 50,000, he can buy 50000 ÷ 500, i.e., 100 rucksacks. But he can only store 60 pieces. Therefore, he can only buy 60 rucksacks, which will give a profit of Rs (60 × 75), i.e., Rs 4500.
There are other possibilities too, like he may choose to buy 10 tents and 50 rucksacks, as his storage is limited to only 60 pieces. The total profit would be calculated as Rs (10 × 250 + 50 × 75), i.e., Rs 6250, and so on.
Thus, we find that the dealer can invest his money in many different ways so that he would earn different profits by the given different investment strategies.
Now the question arises, how should he invest to get the maximum profit? For this, let us see the process mathematically.
Mathematical Formulation of the Problem
Let x be the number of tents and y be the number of rucksacks that the dealer buys. Here, x and y must be non-negative, i.e.,
$\begin{aligned} & x \geqslant 0 \ldots \ldots \ldots \ldots .1 \\ & y \geqslant 0 \ldots \ldots \ldots \ldots .2 \text { (Non-negative constraints) }\end{aligned}$
Mathematically,
2500x + 500y ≤ 50000 (investment)
or 5x + y ≤ 100 ... (3)
and x + y ≤ 60 (storage) ... (4)
Z = 250x + 75y ( objective function) ... (5)
Now, the given problems reduce to:
Maximize Z = 250x + 75y
5x + y ≤ 100
x + y ≤ 60
x ≥ 0, y ≥ 0
Such a problem is called linear programming.
Some Basic Terminology
Objective function
Let Z = ax + by be a linear function, where a, b are the constants.
The linear objective function goes by the computation of the maximum or the minimum of X
Let Z = ax + by be a linear objective function.
Then the variables x and y are called decision variables.
Constraints
Constraints are the limitations or restrictions imposed on the decision variables.
Optimisation problem
A problem that asks to maximise or minimise a linear function limited to certain constraints.
Graphical Method Of Solving Linear Programming Problems
Let us see a graph.
5x + y ≤ 100 ... (1)
x + y ≤ 60 ... (2)
x ≥ 0 ... (3)
y ≥ 0 ... (4)
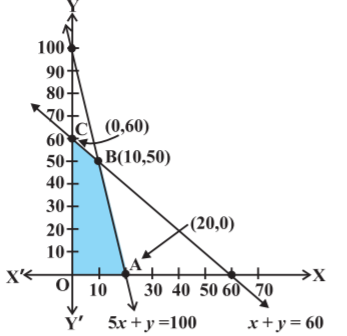
Each point in the shaded region represents a feasible choice; therefore, it is called the feasible region.
Any points outside feasible points are called infeasible points.
Optimal (feasible) solution
Any point in the feasible region that gives the maximum or minimum value of the objective function is called an optimal solution.
Methods Of Solving A Linear Problem
-
Find the feasible region of the problem and find the vertices.
-
Find the objective function Z = ax + by. Let M and m be the largest and the smallest points of the problem
-
i) When the area is bounded. "M" and "m" are maximum and minimum values.
If a feasible area is unbounded, then
-
ax + by > M, no common points with the feasible region.
- ax + by < m, no common points with the feasible region.
Different Types of Linear Programming Problems
-
Manufacturing Problem: Here, we describe the different types of units that should be produced in a firm
-
Diet Problems: Here, we discuss the requirements of essential nutrients for our bodies.
-
Transportation Problem: Here, we discuss the cheapest way of transporting materials from factories to different locations
How to Use the Linear Programming Class 12 Notes Effectively?
Linear Programming is an important chapter of Class 12 Maths that teaches us how to find the best possible solution under given conditions. It helps us learn how to maximise or minimise quantities in real-life situations. This chapter is also useful for JEE basics, and using Class 12 Maths chapter 12 notes properly can make these problems easy to solve. Here are some more points on how these notes are important.
- First, understand what a linear programming problem is and learn how to form the correct mathematical model.
- Practice drawing graphs for constraints and identifying feasible regions, as this is the key to solving LPP questions.
- This chapter is helpful in higher studies and practical fields, so revising with these NCERT Class 12 Maths chapter 12 notes will build a strong base.
- Solve NCERT examples and exercises to improve accuracy and learn how to handle different types of LPP problems.
Linear Programming Class 12 Notes: Previous Year Question and Answer
Given below are selected previous year question answers for NCERT Class 12 Maths Chapter 12 Linear Programming, collected from various examinations.
Question 1:
Given the following two constraints, which solution is a feasible solution for a maximisation problem?
Constraint 1: $4 x_1+3 x_2 \leq 18$
Constraint 2: $x_1-x_2 \leq 3$
Different Types of Linear Programming Problems:
We know that the Corner Point Method is used to solve an LPP graphically, which is based on the principle of the extreme points theorem.
$4 x_1+3 x_2 \leq 18$
$x_1-x_2 \leq 3$
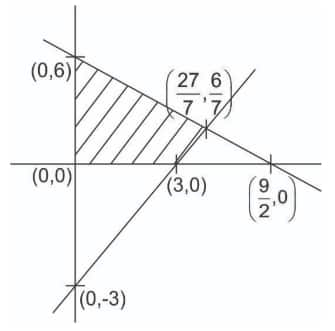
From the figure, only (2, 1) lies in the region.
Hence, the correct answer is $x_1, x_2=(2,1)$
Question 2:
Solve the following linear programming problem graphically :
Maximise $Z =20 x+30 y$
Subject to the constraints :
$
\begin{aligned}
& x+y \leq 80 \\
& 2 x+3 y \geq 100 \\
& x \geq 14 \\
& y \geq 14
\end{aligned}
$
Solution:
The objective is to Maximize $Z = 20x + 30y$
Subject to constraints:
$x + y \leq 80 $
$2x + 3y \geq 100$
$x \geq 14 $
$y \geq 14$
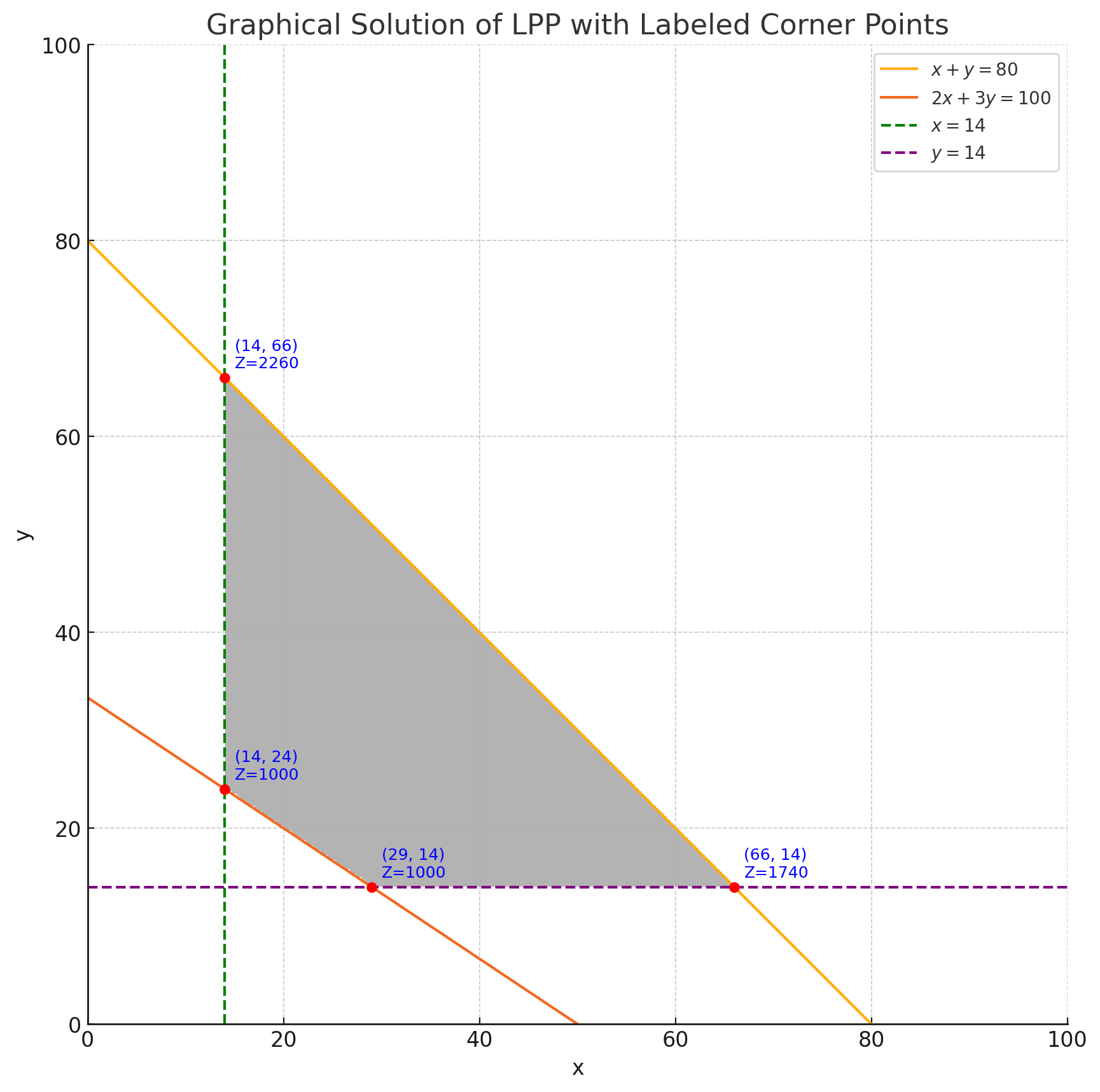
Here are the feasible corner points and the corresponding values of the objective function $Z=20x+30y$ :
At $(14,66), Z=2260$
At $(66,14), Z=1740$
At $(14,24), Z=1000$
At $(29,14), Z=1000$
Maximum value of $Z = 2260$ at $(14, 66)$.
Hence, the correct answer is ($Z = 2260$ at $(14, 66)$).
Question 3:
The corner points of the feasible region in graphical representation of an L.P.P. are $(2,72),(15,20)$, and $(40,15)$. If $Z=18 x+9 y$ be the objective function, then
Solution:
We are given the objective function
$Z=18 x+9 y$
Corner points (vertices) of the feasible region
$A(2,72)$
$B(15,20)$
$C(40,15)$
At $A(2,72)$
$Z=18(2)+9(72)=36+648=684$
At $B(15,20)$
$Z=18(15)+9(20)=270+180=450$
At $C(40,15)$
$Z=18(40)+9(15)=720+135=855$
Minimum value of $Z=450$ at point $(15,20)$
Maximum value of $Z=855$ at point $(40,15)$
Hence, the correct answer is "Z is maximum at $(40,15)$, minimum at $(15,20)$".
NCERT Class 12 Maths Notes Chapter-Wise Links
Access all NCERT Class 12 Maths notes from one place using the links below.
NCERT Exemplar Solutions Subject-Wise
After finishing the textbook exercises, students can use the following links to check the NCERT exemplar solutions for a better understanding of the concepts.
- NCERT Exemplar Class 12 Solutions
- NCERT Exemplar Class 12 Maths
- NCERT Exemplar Class 12 Physics
- NCERT Exemplar Class 12 Chemistry
- NCERT Exemplar Class 12 Biology
NCERT Solutions Subject-Wise
Students can also check these well-structured, subject-wise solutions from the following links.
- NCERT Solutions for Class 12 Mathematics
- NCERT Solutions for Class 12 Chemistry
- NCERT Solutions for Class 12 Physics
- NCERT Solutions for Class 12 Biology
NCERT Books and Syllabus
Students should always analyse the latest syllabus before making a study routine. The following links will help them check the syllabus. Also, students can check some reference books from the following links.
Frequently Asked Questions (FAQs)
Linear Programming is a mathematical technique used for optimisation problems where a linear objective function is maximised or minimised, subject to a set of linear constraints.
It is widely used in economics, business, and engineering for decision-making.
Linear Programming in Class 12th is a very important chapter. The weightage for this chapter can vary slightly from year to year, but it is usually 4 to 6 marks out of the total 80 marks.
The different types are:
Solving linear programming by the Simplex method
Solving linear programming using R
Solving linear programming by the graphical method
Solving linear programming with the use of an open solver.
The objective function in an LPP is a linear equation that defines the goal of the problem. It could be a profit function to maximise profit or a cost function to minimise cost.
The objective function is typically written in the form Z = ax + by, where a and b are constants.
These are the types of questions you will find created for linear programming. These are discussed in length in the linear programming class 12 notes of Careers360.
Graphical Method: Drawing graphs and finding the feasible region to solve the problem.
Formulation of LPP: Translating real-world problems into Linear Programming Formulations.
Maximisation/Minimisation: Solving problems related to maximising profit or minimising cost, given a set of constraints.
Verification of Optimal Solution: Identifying and verifying the optimal solution using corner points.
Popular Questions
Courses After 12th
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
