NCERT Solutions for Class 12 Physics Chapter 7 - Alternating Current

Q7.1 (a) A $100\Omega$ resistor is connected to a $220\: V$ , $50\: Hz$ ac supply.

a)What is the RMS value of current?

Answer:

Given,

RMS voltage in the circuit $V_{rms}=220V$

Resistance in the circuit $R=100\Omega$

Now,

RMS current in the circuit:

$I_{rms}=\frac{V_{rms}}{R}=\frac{220}{100}=2.2A$

Hence, the RMS value of the current is 2.2A.

Q7.1 (b) A $100\Omega$ resistor is connected to a $220\: V$ , $50\: Hz$ ac supply.

What is the net power consumed over a full cycle?

Answer:

Given,

Supplied RMS Voltage $V_{rms}=220V$

Supplied RMS Current $I_{rms}=2.2A$

The net power consumed over a full cycle:

$P=V_{rms}I_{rms}=220*2.2=484W$

Hence net power consumed is 484W.

Q7.2 (a) The peak voltage of an ac supply is $300 V$ . What is the RMS voltage?

Answer:

Given

Peak Value of ac supply:

$V_{peak}=300V$

Now as we know in any sinusoidal function

$RMSvalue=\frac{peakvalue}{\sqrt{2}}$

Since our ac voltage supply is also sinusoidal

$V_{rms}=\frac{V_{peak}}{\sqrt{2}}=\frac{300}{\sqrt{2}}=212.13V$

Hence RMS value of voltage os 212.13V.

Q7.2 (b) The RMS value of current in an ac circuit is $10\: A$ . What is the peak current?

Answer:

Given,

RMS value of current $I_{rms}=10A$

Since Current is also sinusoidal (because only resistance is present in the circuit, not the capacitor and inductor)

$I_{rms}=\frac{I_{peak}}{\sqrt{2}}$

$I_{peak}=\sqrt{2}I_{rms}=\sqrt{2}*10=14.1A$

Hence the peak value of current is 14.1A.

Q7.3 A $44\: mH$ inductor is connected to $220\: V$ , $50\: Hz$ ac supply. Determine the RMS value of the current in the circuit.

Answer:

Given

Supply Voltage $V=220V$

Supply Frequency $f=50Hz$

The inductance of the inductor connected $L=44mH=44*10^{-3}H$

Now

Inductive Reactance

$X_L=\omega L=2\pi fL=2\pi *50*44*10^{-3}$

RMS Value of the current :

$I_{rms}=\frac{V_{rms}}{X_L}= \frac{220}{2\pi *50*44*10^{-3}}=15.92A$

Hence the RMS Value of current is 15.92A.

Q7.4 A $60\mu F$ capacitor is connected to a $100\: V$ , $60\; Hz$ ac supply. Determine the rms value of the current in the circuit.

Answer:

Given,

Supply Voltage $V = 110V$

Supply Frequency $f=60Hz$

The capacitance of the connected capacitor $C=60\mu F=60*10^{-6}F$

Now,

Capacitive Reactance

$X_C=\frac{1}{\omega C}=\frac{1}{2\pi fC}=\frac{1}{2\pi *60*60*10^{-6}}$

RMS Value of current

$I_{rms}=\frac{V_{rms}}{X_C}=V\omega C=V2\pi fC=110*2\pi *60*60*10^{-6}=2.49A$

Hence the RMS Value of current is 2.49A.

Q7.5 In Exercises 7.3 and 7.4, what is the net power absorbed by each circuit over a complete cycle. Explain your answer.

Answer:

As we know,

Power absorbed $P=VIcos\phi$

Where $\phi$ is the phase difference between voltage and current.

$\phi$ for the inductive circuit is -90 degree and $\phi$ for the capacitive circuit is +90 degree.

In both cases (inductive and capacitive), the power absorbed by the circuit is zero because in both cases the phase difference between current and voltage is 90 degree.

This can be seen as The elements(Inductor and Capacitor) are not absorbing the power, rather storing it. The capacitor is storing energy in electrostatic form and Inductor is storing the energy in magnetic form.

Q7.6 A charged $30\mu F$ capacitor is connected to a $27mH$ inductor. What is the angular frequency of free oscillations of the circuit?

Answer:

Given

Capacitance $C=30\mu F=30*10^{-6}$

Inductance $L = 27mH = 27*10^{-3}H$

Now,

Angular Frequency

$\omega _r=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{30*10^{-6}*27*10^{-3}}}=1.11*10^{3}rad/sec$

Hence Angular Frequency is $1.11*10^{3}rad/sec$

Q7.7 A series LCR circuit with $R=20\Omega$ , $L=1.5H$ and $c=35\mu F$ is connected to a variable-frequency $200\; V$ ac supply. When the frequency of the supply equals the natural frequency of the circuit, what is the average power transferred to the circuit in one complete cycle?

Answer:

Given,

Resistance $R=20\Omega$

Inductance $L=1.5H$

Capacitance $C=35\mu F=35*10^{-6}F$

Voltage supply $V = 200V$

At resonance, the supply frequency is equal to the natural frequency, and at the natural frequency, the total impedance of the circuit is equal to the resistance of the circuit

as inductive and capacitive reactance cancel each other. in other words,

$Z = \sqrt{\left ( \omega L-\frac{1}{\omega C} \right )^2+R^2}=\sqrt{0^2+R^2}=R=20\Omega$

As

$\omega L=\frac{1}{\omega C}$

Now,

Current in the circuit

$I=\frac{V}{Z}=\frac{200}{20}=10A$

Average Power transferred in the circuit :

$P=VI=200*10=2000W$

Hence average power transferred is 2000W.

Q7.8 (a) Figure shows a series LCR circuit connected to a variable frequency $230\: V$ source. $L=5.0H$ , $C=80\mu F$ , $R=40\Omega$ .

(a) Determine the source frequency which drives the circuit in resonance.

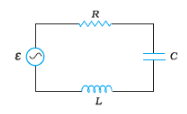
Answer:

Given,

Variable frequency supply voltage $V$ = 230V

Inductance $L=5.0H$

Capacitance $C=80\mu F=80*10^{-6}F$

Resistance $R=40\Omega$

a) Resonance angular frequency in this circuit is given by :

$w_{resonance}=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{5*80*10^{-6}}}=\frac{1000}{20}=50rad/sec$

Hence this circuit will be in resonance when the supply frequency is 50 rad/sec.

Q7.8 (b) Figure shows a series LCR circuit connected to a variable frequency $230\: V$ source.

$L=5.0H$ , $C=80\mu F$ , $R=40\Omega$ .

(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.

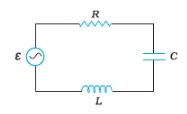
Answer:

Given,

Variable frequency supply voltage $V$ = 230V

Inductance $L=5.0H$

Capacitance $C=80\mu F=80*10^{-6}F$

Resistance $R=40\Omega$

Now,

The impedance of the circuit is

$Z=\sqrt{(wL-\frac{1}{wC})^2+R^2}$

At Resonance Condition

$wL=\frac{1}{wC}$

$Z=R=40\Omega$

Hence, the Impedance at resonance is 40 $\Omega$ .

Now, at resonance condition, impedance is minimum which means the current is maximum which will happen when we have a peak voltage, so

Current in the Resonance circuit is Given by

$I_{resonance}=\frac{V_{peak}}{Z}=\frac{\sqrt{2}* 230}{40}=8.13A$

Hence amplitude of the current at resonance is 8.13A.

Q7.8 (c)Figure shows a series LCR circuit connected to a variable frequency $230\: V$ source.

$L=5.0H$ , $C=80\mu F$ , $R=40\Omega$ .

Determine the rms potential drops across the three elements of the circuit. Show that the potential drop across the LC combination is zero at the resonating frequency.

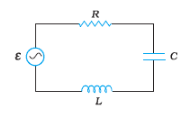
Answer:

Potential difference across any element = $I_{rms}*(impedance)$

$I_{rms}=\frac{I_{peak}}{\sqrt{2}}=\frac{8.13}{\sqrt{2}}=5.85A$

Now

The potential difference across the capacitor:

$V_{capacitor}=I_{rms}*\left (\frac{1}{w_{resonance}C} \right ) =5.85*\left ( \frac{1}{50*80*10^{-6}} \right )=1437.5V$

The potential difference across the inductor

$V_{inductor}=I_{rms}*(w_{resonance}L) =5.85* 50*5=1437.5V$

The potential difference across Resistor

=40 Irms=230V

The potential difference across LC combination

$V_{LC}=I_{rms}*\left ( wL-\frac{1}{wC} \right )=5.85*0=0$

Hence at resonating, the frequency potential difference across LC combination is zero.

Additional Questions

Q1. (a) An $LC$ circuit contains a $20mH$ inductor and a $50\mu F$ capacitor with an initial charge of $10mC$ . The resistance of the circuit is negligible. Let the instant the circuit is closed be $t=0$ .

What is the total energy stored initially? Is it conserved during $LC$ oscillations?

Answer :

Given,

The inductance of the inductor:

$L=20mH=20*10^{-3}H$

The capacitance of the capacitor :

$C=50\mu F=50*10^{-6}F$

The initial charge on the capacitor:

$Q=10mC=10*10^{-3}C$

Total energy present at the initial moment:

$E_{initial}=\frac{Q^2}{2C}=\frac{(10*10^{-3})^2}{2*50*10^{-6}}=1J$

Hence initial energy in the circuit is 1J. Since we don't have any power-consuming elements like resistance in the circuit, the energy will be conserved

Q1. (b) An $LC$ circuit contains a $20mH$ inductor and a $50\mu F$ capacitor with an initial charge of $10mC$ . The resistance of the circuit is negligible. Let the instant the circuit is closed be $t=0$ .

What is the natural frequency of the circuit?

Answer:

Given,

The inductance of the inductor:

$L=20mH=20*10^{-3}H$

The capacitance of the capacitor :

$C=50\mu F=50*10^{-6}F$

The initial charge on the capacitor:

$Q=10mC=10*10^{-3}C$

The natural angular frequency of the circuit:

$w_{natural}=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{(20*10^{-3}*50*10^{-6})}}=10^3rad/sec$

Hence the natural angular frequency of the circuit is $10^3rad/sec$ .

The natural frequency of the circuit:

$f_{natural}=\frac{w_{natural}}{2\pi}=\frac{10^3}{2\pi}=159Hz$

Hence the natural frequency of the circuit is 159Hz.

Q1. (c-i) An $LC$ circuit contains a $20mH$ inductor and a $50\mu F$ capacitor with an initial charge of $10mC$ . The resistance of the circuit is negligible. Let the instant the circuit is closed be $t=0$ . At what time is the energy stored completely electrical (i.e., stored in the capacitor)?

Answer:

at any instant, the charge on the capacitor is:

$Q=Q_0cos(w_{natural}t)=Q_0cos(2\pi f_{natural}t)=Q_0cos\left ( \frac{2\pi t}{T} \right )$

Where time period :

$T=\frac{1}{f_{natural}}=\frac{1}{159}=6.28ms$

Now, when the total energy is purely electrical, we can say that

$Q=Q_0$

$Q_0=Q_0cos(\frac{2\pi}{T})$

$cos(\frac{2\pi t}{T})=1$

this is possible when

$t=0,\frac{T}{2},T,\frac{3T}{2}....$

Hence Total energy will be purely electrical(stored in a capacitor) at

$t=0,\frac{T}{2},T,\frac{3T}{2}....$ .

Q1.(c-ii)An $LC$ circuit contains a $20mH$ inductor and a $50\mu F$ capacitor with an initial charge of $10mC$ . The resistance of the circuit is negligible.
Let the instant the circuit is closed be $t=0$ . At what time is the energy stored completely magnetic (i.e., stored in the inductor)?

Answer:

The stored energy will be purely magnetic when the pure electrical stored is zero. i.e. when the charge on the capacitor is zero, all energy will be stored in the inductor.

So, t for which charge on the capacitor is zero is

$t=\frac{T}{4},\frac{3T}{4},\frac{5T}{4}..$

Hence at these times, the total energy will be purely magnetic.

Q1. (d) An $LC$ circuit contains a $20mH$ inductor and a $50\mu F$ capacitor with an initial charge of $10mC$ . The resistance of the circuit is negligible. Let the instant the circuit is closed be $t=0$ . At what times is the total energy shared equally between the inductor and the capacitor?

Answer:

The energy will be shared equally when the energy in the capacitor is half of the maximum energy it can store. i.e.

$\frac{Q^2}{2C}=\frac{1}{2}\frac{Q_0^2}{2C}$

From here, we got

$Q=\frac{Q_0}{\sqrt{2}}$

So now, we know the charge on the capacitor, we can calculate the time for which

$\frac{Q_0}{\sqrt{2}}=Q_0cos\left ( \frac{2\pi t}{T} \right )$

$\frac{1}{\sqrt{2}}=cos\left ( \frac{2\pi t}{T} \right )$

From here,

$t=\frac{T}{8},\frac{3T}{8},\frac{5T}{8}..$

Hence for these times, the total energy will be shared equally between capacitor and inductor.

Q1. (e) An $LC$ circuit contains a $20mH$ inductor and a $50\mu F$ capacitor with an initial charge of $10mC$ . The resistance of the circuit is negligible. Let the instant the circuit is closed be $t=0$ . If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat?

Answer:

If the resistance is added to the circuit, the whole energy will dissipate as heat eventually. energy will keep moving between the capacitor and inductor with reducing in magnitude in each cycle and eventually all energy will be dissipated.

Q2. (a) A coil of inductance $0.50H$ and resistance $100\Omega$ is connected to a $240V$ , $50Hz$ ac supply. What is the maximum current in the coil?

Answer:

Given,

The inductance of the coil $L=0.50H$

The resistance of the coil $R=100\Omega$

Supply voltage $V=240V$

Supply voltage frequency $f=50Hz$

Now, as we know peak voltage = $\sqrt2$ (RMS Voltage)

Peak voltage

$V_{peak}=\sqrt2*240=339.4V$

The impedance of the circuit :

$Z=\sqrt{R^2+(wL)^2}=\sqrt{100^2+(2\pi (.5) *50)^2}$

Now peak current in the circuit :

$I_{peak}=\frac{V_{peak}}{Z}=\frac{339}{\sqrt{100^2+(2\pi (.5) *50)^2}}=1.82A$

Hence peak current is 1.82A in the circuit.

Q2. (b) A coil of inductance $0.50H$ and resistance $100\Omega$ is connected to a $200V$ , $50Hz$ ac supply. What is the time lag between the voltage maximum and the current maximum?

Answer:

Let the voltage in the circuit be

$V = V_0coswt$ and

Current in the circuit be

$I = I_0cos(wt-\phi )$

Where $\phi$ is the phase difference between voltage and current.

V is maximum At

t = 0

$I$ is maximum At

$t=\frac{w}{\phi }$

Hence, the time lag between voltage maximum and the current maximum is

$\frac{w}{\phi }$ .

For phase difference $\phi$ we have

$tan\phi =\frac{wL}{R}=\frac{2\pi *50*0.5}{100}=1.57$

$\phi =57.5^0$

$t=\frac{\phi}{w}=\frac{57.5*\pi}{180*2\pi *50}=3.2ms$

Hence time lag between the maximum voltage and the maximum current is $3.2ms$

Q3 Obtain the answers (a) to (b) ,if the circuit is connected to a high-frequency supply $(240 V\: ,10 kHz)$ . Hence, explain the statement that at very high frequency, an inductor in a circuit nearly amounts to an open circuit. How does an inductor behave in a dc circuit after the steady state?

Answer:

Given,

The inductance of the coil $L=50H$

The resistance of the coil $R=100\Omega$

Supply voltage $V=240V$

Supply voltage frequency $f=10kHz$

a)

Now, as we know peak voltage = $\sqrt2$ (RMS Voltage)

Peak voltage $V_{peak}=\sqrt2*240=339.4V$

Now,

The impedance of the circuit :

$Z=\sqrt{R^2+(wL)^2}=\sqrt{100^2+(2\pi 10*10^3 *50)^2}$

Now peak current in the circuit :

$I_{peak}=\frac{V_{peak}}{Z}=\frac{339}{\sqrt{100^2+(2\pi 10*10^3 *50)^2}}=1.1*10^{-2}A$

Hence peak current is $1.1*10^{-2}A$ in the circuit.

The current in the circuit is very small, which is one of the indications of inductor working as a nearly open circuit in the case of high frequency.

b)

For phase difference $\phi$ we have

$tan\phi =\frac{wL}{R}=\frac{2\pi *10*10^3*0.5}{100}=100\pi$

$\phi =89.82^0$

Now

$t=\frac{\phi}{w}=\frac{89.82*\pi}{180*2\pi *10^3}=25\mu s$

Hence time lag between the maximum voltage and the maximum current is $25\mu s$.

In the DC circuit, after attaining the steady state, inductor behaves line short circuit as $w$ is Zero.

Q4. (a) A $100\mu F$ capacitor in series with a $40\Omega$ resistance is connected to a $110\: V$ , $60\: Hz$ supply.
What is the maximum current in the circuit?

Answer:

Given,

The capacitance of the capacitor $C=100\mu F$

The resistance of the circuit $R=40\Omega$

Voltage supply $V = 100V$

Frequency of voltage supply $f=60Hz$

The maximum current in the circuit

$I_{max}=\frac{V_{max}}{Z}=\frac{\sqrt{2}V}{\sqrt{R^2+\left ( \frac{1}{wC} \right )^2}}=\frac{\sqrt{2}*110}{\sqrt{40^2+\left ( \frac{1}{2\pi *60*100*10^{-6}} \right )^2}}=3.24A$

Hence maximum current in the circuit is 3.24A.

Q4. (b) A $100\mu F$ capacitor in series with a $40\Omega$ resistance is connected to a $110\; V$ , $60\: Hz$ supply. What is the time lag between the current maximum and the voltage maximum?

Answer:

In the case of a capacitor, we have

$tan\phi=\frac{\frac{1}{wC}}{R}=\frac{1}{wCR}$

So,

$tan\phi=\frac{1}{wCR}=\frac{1}{2\pi 60 *100*10^{-6}*40}=0.6635$

$\phi=33.56^0$

So the time lag between max voltage and the max current is :

$t=\frac{\phi }{w}=\frac{33.56\pi}{180*2\pi*60}=1.55ms$

Q5. Obtain the answers to (a) and (b) in Exercise 7.15 if the circuit is connected to a $110\: V$ , $10kHz$ supply? Hence, explain the statement that a capacitor is a conductor at very high frequencies. Compare this behaviour with that of a capacitor in a dc circuit after the steady state.

Answer:

Given,

The capacitance of the capacitor $C=100\mu F$

The resistance of the circuit $R=40\Omega$

Voltage supply $V = 100V$

Frequency of voltage supply $f=12kHz$

The maximum current in the circuit

$I_{max}=\frac{V_{max}}{Z}=\frac{\sqrt{2}V}{\sqrt{R^2+\left ( \frac{1}{wC} \right )^2}}=\frac{\sqrt{2}*110}{\sqrt{40^2+\left ( \frac{1}{2\pi *12*10^3*100*10^{-6}} \right )^2}}=3.9A$

Hence maximum current in the circuit is 3.9A.

b)

In the case of capacitor, we have

$tan\phi=\frac{\frac{1}{wC}}{R}=\frac{1}{wCR}$

So,

$tan\phi=\frac{1}{wCR}=\frac{1}{2\pi 10*10^3 *100*10^{-6}*40}=\frac{1}{96\pi}$

$\phi=0.2^0$

So the time lag between max voltage and max current is :

$t=\frac{\phi }{w}=\frac{0.2\pi}{180*2\pi*60}=0.04\mu s$

At high frequencies, $\phi$ tends to zero. which indicates capacitor acts as a conductor at high frequencies.

In the DC circuit, after a steady state is achieved, Capacitor acts like an open circuit.

Q6. Keeping the source frequency equal to the resonating frequency of the series $LCR$ circuit, if the three elements, $L$ , $C$ and $R$ are arranged in parallel, show that the total current in the parallel $LCR$ circuit is minimum at this frequency. Obtain the current rms value in each branch of the circuit for the elements and source specified in Exercise 7.11 for this frequency.

Answer:

As we know, in the case of a parallel RLC circuit:

$\frac{1}{Z}=\sqrt{\frac{1}{R^2}+(wC-\frac{1}{wL})^2}$

$I=\frac{V}{Z}={V}{\sqrt{\frac{1}{R^2}+\left (wC- \frac{1}{wL} \right )^2}}$

The current will be minimal when

$wC=\frac{1}{wL}$

Which is also the condition of natural frequency. Hence the total current is minimum when source frequency is equal to the natural frequency.

RMS value of current in R

$I_{rms}=\frac{V_{rms}}{R}=\frac{230}{40}=5.75A$

RMS value in Inductor

$I_{inductor}=\frac{V_{rms}}{wL}=\frac{230}{5*50}=0.92A$

RMS value in capacitor

$I_{capacitor}=\frac{V_{rms}}{1/wL}={230*50*80*10^{-6}}=0.92A$

Capacitor current and inductor current will cancel out each other so the current flowing in the circuit is 5.75A.

Q7. (a) A circuit containing a $80mH$ inductor and a $60\mu F$ capacitor in series is connected to a $230\: V$ , $50\: Hz$ supply. The resistance of the circuit is negligible. Obtain the current amplitude and rms values.

Answer:

The inductance of the inductor $L=80mH=80*10^3H$

The capacitance of the capacitor $C=60\mu F$

Voltage supply $V = 230V$

Frequency of voltage supply $f=50Hz$ .

Here, we have

$V=V_{max}sinwt=V_{max}sin2\pi ft$

Impedance

$Z=\sqrt{R^2+\left ( wL-\frac{1}{wC} \right )^2}$

$Z=\sqrt{0^2+\left ( 2\pi*50*80*10^{-3}-\frac{1}{2\pi 50*60*10^{-6}} \right )^2}=8\pi-\frac{1000}{6\pi }$

Now,

Current in the circuit will be

$I=\frac{V}{Z}=\frac{V_{max}sinwt}{Z\angle \phi }=I_{max}sin(wt-\phi )$

where,

$I_{max}=\frac{V_{max}}{Z}=\frac{\sqrt{2}*230}{8\pi-\frac{1000}{6\pi}}=-11.63A$

The negative sign is just a matter of the direction of current.so,

$I=11.63sin(wt-\phi )$

here

$tan\phi=\frac{wL-\frac{1}{wC}}{R}$

But, since the value of R is zero(since our circuit have only L and C)

$\phi=90^0$

Hence

$I=11.63sin(wt-\frac{\pi}{2} )$

Now,

RMS value of this current:

$I_{rms}=\frac{I_{max}}{\sqrt{2}}=\frac{11.63}{\sqrt{2}}=8.22A$ .

Q7. (b) A circuit containing a $80mH$ inductor and a $60\mu F$ capacitor in series is connected to a $230\: V$ , $50\: Hz$ supply. The resistance of the circuit is negligible. Obtain the rms values of potential drops across each element.

Answer:

As we know,

RMS potential drop across an element with impedance Z:

$V_{element}=I_{rms}Z_{element}$

SO,

RMS potential difference across inductor:

$V_{inductor}=I_{rms}*wL=8.22*2\pi *60*80*10^{-3}=206.61V$

RMS potential drop across capacitor

$V_{capacitor}=I_{rms}*\frac{1}{wC}=8.22*\frac{1}{2\pi*60*60*10^{-6}}=436.3V$

Q7. (c) A circuit containing a $80mH$ inductor and a $60\mu F$ capacitor in series is connected to a $230\: V$ , $50\: Hz$ supply. The resistance of the circuit is negligible

(c) What is the average power transferred to the inductor?

Answer:

Since

$I=I_{max}sin(wt-\phi )$

Current flowing in the circuit is sinusoidal and hence average power will be zero as the average of sin function is zero.in other words, the inductor will store energy in the positive half cycle of the sin (0 degrees to 180 degrees) and will release that energy in the negative half cycle(180 degrees to 360 degrees), and hence average power is zero.

Q7. (d) A circuit containing a $80mH$ inductor and a $60\mu F$ capacitor in series is connected to a $230\: V$ , $50\: Hz$ supply. The resistance of the circuit is negligible . What is the average power transferred to the capacitor?

Answer:

As we know,

Average power $P=VIcos\theta$ where $\theta$ is the phase difference between voltage and current.

Since in the circuit, phase difference $\theta$ is $\pi/2$ , the average power is zero.

Q7. (e) A circuit containing a $80mH$ inductor and a $60\mu F$ capacitor in series is connected to a $230\: V$ , $50\: Hz$ supply. The resistance of the circuit is negligible . What is the total average power absorbed by the circuit? [‘Average’ implies ‘averaged over one cycle’.]

Answer:

Since the phase difference between voltage and current is 90 degree, even the total power absorbed by the circuit is zero. This is an ideal circuit, we can not have any circuit in practical that consumes no power, that is because practically resistance of any circuit is never zero. Here only inductor and capacitor are present and none of them consumes energy, they just store it and transfer it like they are doing it in this case.

Q8. Suppose the circuit in Exercise 7.18 has a resistance of $15\Omega$ . Obtain the average power transferred to each element of the circuit, and the total power absorbed.

Answer:

The inductance of the inductor $L=80mH=80*10^3H$

The capacitance of the capacitor $C=60\mu F$

The resistance of a $15\Omega$ resistor

Voltage supply $V = 230V$

Frequency of voltage supply $f=50Hz$

As we know,

Impedance

$Z=\sqrt{R^2+\left ( wL-\frac{1}{wC} \right )^2}$

$Z=\sqrt{15^2+\left ( 2\pi*50*80*10^{-3}-\frac{1}{2\pi 50*60*10^{-6}} \right )^2}=31.728$

Current flowing in the circuit :

$I=\frac{V}{Z}=\frac{230}{31.72}=7.25A$

Now,

Average power transferred to the resistor:

$P_{resistor}=I^2R=(7.25)^2*15=788.44W$

Average power transferred to the inductor = 0

Average power transferred to the capacitor = 0:

Total power absorbed by circuit :

$P_{resistor}+p_{inductor}+P_{capacitor}=788.44+0+0=788.44W$

Hence circuit absorbs 788.44W.

Q9. (a) A series LCR circuit with $L=0.12H$ , $C=480nF$ , $R=23\Omega$ is connected to a $230V$ variable frequency supply.

What is the source frequency for which current amplitude is maximum. Obtain this maximum value.

Answer:

The inductance of the inductor $L=0.12H$

The capacitance of the capacitor $C=480n F$

The resistance of the resistor $R=23\Omega$

Voltage supply $V = 230V$

Frequency of voltage supply $f=50Hz$

As we know,

the current amplitude is maximum at the natural frequency of oscillation, which is

$w_{natural}=\sqrt\frac{1}{LC}=\frac{1}{\sqrt{0.12*480*10^{-9}})}=4166.67rad/sec$

Also, at this frequency,

$Z=R=23$

SO,

The maximum current in the circuit :

$I_{max}=\frac{V_{max}}{Z}=\frac{V_{max}}{R}=\frac{\sqrt{2*}230}{23}=14.14A$

Hence maximum current is 14.14A.

Q9. (b) A series LCR circuit with $L=0.12H$ , $C=480nF$ , $R=23\Omega$ is connected to a $230V$ variable frequency supply.

What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.

Answer:

Since the resistor is the only element in the circuit which consumes the power, the maximum absorbed power by circuit will be maximum when power absorbed by the resistor will be maximum. power absorbed by the resistor will be maximum at when current is maximum which is the natural frequency case,

Hence when source frequency will be equal to the natural frequency, the power absorbed will be maximum.

Hence frequency

$f=\frac{w_r}{2\pi}=\frac{4166.67}{2\pi}=663.48Hz$

Maximum Power Absorbed

$P=I^2R=(14.14)^2*23=2299.3W$ .

Q9. (c) A series LCR circuit with $L=0.12H$ , $C=480nF$ , $R=23\Omega$ is connected to a $230V$ variable frequency supply . What is the $Q$ factor of the given circuit?

Answer:

The value of maximum angular frequency is calculated in the first part of the question and whose magnitude is 4166.67

Q-factor of any circuit is given by

$Q=\frac{w_rL}{R}=\frac{4166.67*0.12}{23}=21.74$

Hence Q-factor for the circuit is 21.74.

Q9. (d) A series LCR circuit with $L=0.12H$ , $C=480nF$ , $R=23\Omega$ is connected to a $230V$ variable frequency supply. For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?

Answer:

As

Power $P=I^2R$

Power $P$ will be half when the current $I$ is $1/\sqrt{2}$ times the maximum current.

As,

$I =I_{max}Sin(wt-\phi)$

At half powerpoint :

$\frac{i_{max}}{\sqrt{2}} =I_{max}Sin(wt-\phi)$

$\frac{1}{\sqrt{2}} =Sin(wt-\phi)$

$wt=\phi+\frac{\pi}{4}$

here,

$\phi=tan^{-1}(\frac{wL-\frac{1}{wC}}{R})$

On putting values, we get, two values of $w$ for which

$wt=\phi+\frac{\pi}{4}$

And they are:

$w_1=678.75Hz$

$w_2=648.22Hz$

Also,

The current amplitude at these frequencies

$I_{halfpowerpoint}=\frac{I_{max}}{\sqrt{2}}=\frac{14.14}{1.414}=10A$

Q10. Obtain the resonant frequency and $\varrho$ -factor of a series $LCR$ circuit with $L=0.3H$ , $C=27\mu F$ , and $R=7.4\Omega$ . It is desired to improve the sharpness of the resonance of the circuit by reducing its ‘full width at half maximum’ by a factor of 2. Suggest a suitable way.

Answer:

The inductance of the inductor $L=0.3H$

The capacitance of the capacitor $C=27\mu F$

The resistance of the resistor $R=7.4\Omega$

Now,

Resonant frequency

$w_r=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{0.3*27*10^{-6}}}=111.11rad/sec$

Q-Factor of the circuit

$Q=\frac{w_rL}{R}=\frac{111.11*0.3}{7.4}=45.0446$

Now, to improve the sharpness of resonance by reducing its full width at half maximum, by a factor of 2 without changing $w_r$ ,

we have to change the resistance of the resistor to half of its value, that is

$R_{new}=\frac{R}{2}=\frac{7.4}{2}=3.7\Omega$

Q11. (a) In any ac circuit, is the applied instantaneous voltage equal to the algebraic sum of the instantaneous voltages across the series elements of the circuit? Is the same true for rms voltage?

Answer:

Yes, at any instant the applied voltage will be distributed among all element and the sum of the instantaneous voltage of all elements will be equal to the applied. But this is not the case in RMS because all elements are varying differently and they may not be in the phase.

Q11.(b) Answer the following questions: A capacitor is used in the primary circuit of an induction coil.

Answer:

Yes, we use capacitors in the primary circuit of an induction coil to avoid sparking. when the circuit breaks, a large emf is induced and the capacitor gets charged from this avoiding the case of sparking and short circuit.

Q11. (c) Answer the following questions:

An applied voltage signal consists of a superposition of a $dc$ voltage and an ac voltage of high frequency. The circuit consists of an inductor and a capacitor in series. Show that the dc signal will appear across $C$ and the ac signal across $L$ .

Answer:

For a high frequency, the inductive reactance and capacitive reactance:

$X_L=wL=Large \:value\: And \:X_C = \frac{1}{wC}=Very\:small$

Hence the capacitor does not offer resistance to a higher frequency, so the ac voltage appears across L.

Similarly

For DC, the inductive reactance and capacitive reactance:

$X_L=wL=Very\:small\: And \:X_C = \frac{1}{wC}=Large \:value$

Hence DC signal appears across Capacitor only.

Q11.(d) Answer the following questions:

A choke coil in series with a lamp is connected to a dc line. The lamp is seen to shine brightly. Insertion of an iron core in the choke causes no change in the lamp’s brightness. Predict the corresponding observations if the connection is to an ac line.

Answer:

For a steady state DC, the increasing inductance value by inserting iron core in the choke, has no effect on the brightness of the connected lamp, whereas, for ac when the iron core is inserted, the light of the lamp will shine less brightly because of increase in inductive impedance.

Q11. (e) Answer the following questions:

Why is a choke coil needed in the use of fluorescent tubes with AC mains? Why can we not use an ordinary resistor instead of the choke coil?

Answer:

We need choke coil in the use of fluorescent tubes with ac mains to reduce the voltage across the tube without wasting much power. If we use simply resistor for this purpose, there will be more power loss, hence we do not prefer it.

Q12. A power transmission line feeds input power at $2300 V$ to a stepdown transformer with its primary windings having $40000$ turns. What should be the number of turns in the secondary in order to get output power at $230 V$ ?

Answer:

Given,

Input voltage:

$V_{input}=2300V$

Number of turns in the primary coil

$N_{primary}= 4000$

Output voltage:

$V_{output}=230V$

Now,

Let the number of turns in secondary be

$N=N_{secondary}$

Now as we know, in a transformer,

$\frac{V_{primary}}{V_{secondary}}=\frac{N_{primary}}{N_{secondary}}$

${N_{secondary}} =\frac{V_{secondary}}{V_{primary}}*N_{primary}=\frac{230}{2300}*4000=400$

Hence the number of turns in secondary winding is 400.

Q13. At a hydroelectric power plant, the water pressure head is at a height of $300m$ and the water flow available is $100m^{3}s^{-1}$ . If the turbine generator efficiency is $60^{0}/_{0}$ , estimate the electric power availablefrom the plant $(g=9.8ms^{-2})$ .

Answer:

Given,

Height of the water pressure head

$h=300m$

The volume of the water flow per second

$V=100m^3s^{-1}$

Turbine generator efficiency

$\eta =0.6$

Mass of water flowing per second

$M=100*10^3=10^5kg$

The potential energy stored in the fall for 1 second

$P=Mgh=10^5*9.8*300=294*10^6J$

Hence input power

$P_{input}=294*10^6J/s$

Now as we know,

$\eta =\frac{P_{output}}{P_{input}}$

$P_{output}=\eta *P_{input}=0.6*294*10^6=176.4*10^6W$

Hence output power is 176.4 MW.

Q14. (a) A small town with a demand of $800 kW$ of electric power at $220V$ is situated $15km$ away from an electric plant generating power at $440V$ . The resistance of the two wire line carrying power is $0.5\Omega$ per km. The town gets power from the line through a $4000-220V$ step-down transformer at a sub-station in the town. Estimate the line power loss in the form of heat.

Answer:

Power required

$P=800kW=800*10^3kW$

The total resistance of the two-wire line

$R=2*15*0.5=15\Omega$

Input Voltage

$V_{input}=4000V$

Output Voltage:

$V_{output}=220V$

RMS Current in the wireline

$I=\frac{P}{V_{input}}=\frac{800*10^3}{4000}=200A$

Now,

Power loss in the line

$P_{loss}=I^2R=200^2*15=600*10^3=600kW$

Hence, power loss in line is 600kW.

Q14. (b) A small town with a demand of $800 kW$ of electric power at $220V$ is situated $15km$ away from an electric plant generating power at $440V$ . The resistance of the two wire line carrying power is $0.5\Omega$ per km. The town gets power from the line through a $4000-220V$ step-down transformer at a sub-station in the town.

How much power must the plant supply, assuming there is negligible power loss due to leakage?

Answer:

Power required

$P=800kW=800*10^3kW$

The total resistance of the two-wire line

$R=2*15*0.5=15\Omega$

Input voltage

$V_{input}=4000V$

Output voltage:

$V_{output}=220V$

RMS current in the wireline

$I=\frac{P}{V_{input}}=\frac{800*10^3}{4000}=200A$

Now,

Total power delivered by plant = line power loss + required electric power = 800 + 600 = 1400kW.

Q14.(c) A small town with a demand of $800 kW$ of electric power at $220V$ is situated $15km$ away from an electric plant generating power at $440V$ . The resistance of the two wire line carrying power is $0.5\Omega$ per km. The town gets power from the line through a $4000-220V$ step-down transformer at a sub-station in the town. Characterise the step up transformer at the plant.

Answer:

Power required

$P=800kW=800*10^3kW$

The total resistance of the two-wire line

$R=2*15*0.5=15\Omega$

Input Voltage

$V_{input}=4000V$

Output Voltage:

$V_{output}=220V$

RMS Current in the wireline

$I=\frac{P}{V_{input}}=\frac{800*10^3}{4000}=200A$

Now,

Voltage drop in the power line = $IR=200*15=3000V$

Total voltage transmitted from the plant = 3000+4000=7000

as power is generated at 440V, The rating of the power plant is 440V-7000V.

Q15. Do the same exercise as above with the replacement of the earlier transformer by a $40,000-220V$ step-down transformer (Neglect, as before, leakage losses though this may not be a good assumption any longer because of the very high voltage transmission involved). Hence, explain why high voltage transmission is preferred.

Answer:

Power required

$P=800kW=800*10^3kW$

The total resistance of the two-wire line

$R=2*15*0.5=15\Omega$

Input Voltage

$V_{input}=40000V$

Output Voltage:

$V_{output}=220V$

RMS current in the wireline

$I=\frac{P}{V_{input}}=\frac{800*10^3}{40000}=20A$

Now,

a) power loss in the line

$P_{loss}=I^2R=20^2*15=6kW$

b)

Power supplied by plant = 800 kW + 6 kW = 806 kW.

c)

Voltage drop in the power line = $IR=20*15=300V$

Total voltage transmitted from the plant = 300+40000=40300

as power is generated at 440V, The rating of the power plant is 440V-40300V.

We prefer high voltage transmission because power loss is a lot less than low voltage transmission.