The NCERT Solutions for Class 12 Chemistry Chapter 1 Solutions cover all the important topics included in the syllabus in a well structured manner. They help students understand each concept clearly and practise questions topic-wise for better exam preparation. Topics covered in this chapter are given below:
NCERT Solutions for Class 12 Chemistry Chapter 1 - Solutions
Upcoming Event
CBSE Class 12th Exam Date:17 Feb' 26 - 17 Feb' 26
Have you ever stirred salt or sugar in water and watched it disappear? This is more than just mixing it is the formation of a solution. A solution is a homogeneous mixture of two or more compounds. It helps answer several interesting questions, such as: What makes a solute dissolve in a solvent? Why does adding salt to water raise its temperature? How does antifreeze protect cars in winter? You will also explore fascinating concepts like colligative properties and learn how solutions can alter boiling and freezing points.
This Story also Contains
- NCERT Solutions for Class 12 Chemistry Chapter 1: Download PDF
- NCERT Solution for Class 12 Chapter 1 (Intext Questions)
- NCERT Solutions for Class 12 Chemistry Chapter 1 (Exercise Questions)
- Class 12 Chemistry NCERT Chapter 1: Higher Order Thinking Skills (HOTS) Questions
- Approaches to Solve Problems of Chapter 1 Chemistry Class 12
- Topics of NCERT Syllabus Class 12 Chemistry Solutions
- What Extra Should Students Study Beyond the NCERT for JEE/NEET?
- What Students Learn from NCERT Solutions for Class 12 Chemistry Chapter 1 Solutions
- Importance of Class 12 Chemistry Chapter 1 – Solutions
- NCERT solutions for class 12 chemistry
- NCERT Exemplar Class 12 Solutions
- NCERT Solutions for Class 12: Other Subjects
- NCERT Books and NCERT Syllabus
These NCERT Solutions for Class 12 Chemistry provide simple explanations for every question in the textbook. They are designed to help students develop analytical and critical thinking skills. To further enhance logical reasoning and problem-solving ability, carefully selected HOTS questions are also included. Step by step solutions for all exercises are provided below, students can scroll down to access them.
NCERT Solutions for Class 12 Chemistry Chapter 1: Download PDF
Students can download the class 12 chemistry chapter 1 solutions question answer pdf for free. These solutions of NCERT are designed to help you understand the fundamental concepts and solve textbook questions with ease. They give simple, easy answers that help you understand tough topics.
Download PDFAlso read:
NCERT Solution for Class 12 Chapter 1 (Intext Questions)
Here are detailed and accurate solutions class 12 question answer for Intext Questions.They help students understand the concepts and make it easier to revise important topics for exams. These NCERT Solutions for Class 12 will help in better concept clarity and exam preparation.
Answer:
We know that solute and solvent forms solution.
So mass percentage of benzene (solute) :-
$=\frac{22}{22+122} \times 100$
=$\frac{22}{144} \times 100$
$=15.28 \%$
Similarly mass percentage of CCl4 :-
$=\frac{122}{22+122} \times 100$
$=\frac{122}{144} \times 100$
$=84.72 \%$
Question 1.2 Calculate the mole fraction of benzene in solution containing $30\%$ by mass in carbon tetrachloride.
Answer :
For calculating mole fraction, we need moles of both the compounds.
It is given that benzene is $30\%$ in the solution by mass.
So if we consider 100g of solution then 30g is benzene and 70g is CCl4 .
Moles of CCl $_4=\frac{\text { Given mass }}{\text { Molar mass }}$
$=\frac{70}{154}=0.4545 \mathrm{~mol}$
$\left ( Molar\ mass\ of\ CCl_4 = 12 + 4(35.5) \right )$
Similarly moles of benzene :
$=\frac{30}{78}$
$=0.3846$
(Molar mass of benzene $=6(12)+6(1))$
So mole fraction of benzene is given :
$=\frac{0.3846}{0.3846+0.4545}$
$= 0.458$
Question 1.3(a) Calculate the molarity of each of the following solutions:
$30\; g$ of $Co(NO_{3})_{2}.\; 6H_{2}O$ in $4.3\: L$ of solution
Answer :
For finding molarity we need the moles of solute and volume of solution.
So moles of solute :
$=\frac{\text { Given mass }}{\text { Molar mass }}$
$=\frac{30}{291}=0.103$
Since molar mass of $\mathrm{Co}\left(\mathrm{NO}_3\right)_2 \cdot 6 \mathrm{H}_2 \mathrm{O}=59+2(14+316)+6(16+12)$
$=291 \mathrm{~g} \mathrm{~mol}^{-1}$
Now, $Molarity = \frac{No.\ of\ moles\ of\ solute}{Volume\ of\ solution\ (l)}$
$= \frac{0.103}{4.3} = 0.023\ M$
Question 1.3(b) Calculate the molarity of each of the following solutions:
$30\; mL$ of $0.5\; M$ $H_{2}SO_{4}$ diluted to $500 \; mL$ .
Answer :
By conservation of moles we can write :
M1V1 = M2V2
Given that M1= 0.5 M and V1 = 30 ml ; V2 = 500 ml
$M_2 = \frac{M_1V_1}{V_2} = 0.03\ M$
Question 1.4 Calculate the mass of urea $(NH_{2}CONH_{2})$ required in making $2.5 \; kg$ of $0.25\; molal$ aqueous solution.
Answer :
Let us assume that the mass of urea required be x g.
So moles of urea will be :
$Moles = \frac{Given\ mass}{Molar\ mass} = \frac{x}{60}\ moles$
Molality $=\frac{\text { Moles }}{\text { Mass of solvent in } \mathrm{Kg}}$
$=\frac{\frac{x}{60}}{2.5-0.001 x}=0.25$
we get x = 37
Thus mass of urea required = 37 g.
Question 1.5 Calculate
(a) molality
(b) molarity and
(c) mole fraction
of KI if the density of $20\%$ (mass/mass) aqueous KI is $1.202\; g\; mL^{-1}$ .
Answer :
If we assume our solution is 100 g. Then according to question, 20 g KI is present and 80 g is water.
So moles of KI :
$=\frac{20}{166}$ $\left ( Molar\ mass = 39+127 = 166\ g\ mol^{-1} \right )$
(a) Molality :-
Molality $=\frac{\text { Moles }}{\text { Mass of solvent in Kg }}$
$=\frac{\frac{20}{166}}{0.08}=1.506 \mathrm{~m}$.
(b) Molarity :-
$Density = \frac{Mass}{Volume}$
Volume $=\frac{\text { Mass }}{\text { Density }}$
$=\frac{100}{1.202}=83.19 \mathrm{~mL}$
Molarity $=\frac{\text { Moles }}{\text { Volume }(l)}$
$=\frac{\frac{20}{166}}{83.19 \times 10^{-3}}=1.45 \mathrm{M}$
(c) Mol fraction = Moles of water :-
$= \frac{80}{18} = 4.44$
So, mol fraction of KI :-
$= \frac{0.12}{0.12+4.44} = 0.0263$
Page- 9
Answer :
For finding Henry's constant we need to know about the mole fraction of H2S.
Solubility of H2S in water is given to be 0.195 m .
i.e., 0.195 moles in 1 Kg of water.
$Moles\: of\: water :=\frac{1000}{18} = 55.55\ moles$
So $x_{H_2S} = Mole\ fraction\ of\ H_2S$
$= \frac{0.195}{0.195+55.55} = 0.0035$
At STP conditions, pressure = 1 atm or 0.987 bar
Equation is : $p_{H_2S} = K_h\times x_{H_2S}$
So we get :
$K_h =\frac{0.987}{0.0035} = 282\ bar$
Answer :
We know that ,
$p = k_h\times x$
Pressure of CO2= 2.5 atm
We know that : $1\ atm = 1.01\times10^5\ Pa$
So, Pressure of CO2 = $2.53\times10^5$ Pa
By Henry Law we get,
$x=\frac{p}{k_h}$
$=\frac{2.53 \times 10^5}{1.67 \times 10^8}$
$=1.52 \times 10^{-3}$
Taking density of soda water = 1 g/ml
We get mass of water = 500 g.
So, Moles of water :
$= \frac{500}{18} = 27.78$
Also, $x_{H_2O} = \frac{n_{CO_2}}{n_{H_2O}+n_{CO_2}} \approx \frac{n_{CO_2}}{n_{H_2O}}$
So, moles of CO2= 0.042 mol
Using relation of mole and given mass, we get
Mass of CO2 = 1.848 g.
Page-15
Answer :
Let the composition of liquid A (mole fraction) be x A .
So mole fraction of B will be x B = 1 - x A .
Given that, $P^{\circ}_A = 450\ mm\ of\ Hg\ ;\ P^{\circ}_B = 700\ mm\ of\ Hg$
Using Raoult’s law ,
$p_{total} = p^{\circ}_A\ x_A\ +\ p^{\circ} _B\ (1-x_A)$
Putting values of p total and vapour pressure of pure liquids in the above equation, we get :
600 = 450.x A + 700.(1 - x A )
or 600 - 700 = 450x A - 700x A
or x A = 0.4
and x B = 0.6
Now pressure in vapour phase :
$P_A = p^{\circ}_A\ x_A$
= 450(0.4) = 180 mm of Hg
$P_B = p^{\circ}_B\ x_B$
= 700(0.6) = 420 mm of Hg
$Mole\ fraction\ of\ liquid\ A = \frac{P_A}{P_A\ + P_B }$
$= \frac{180}{180\ + 420 } = 0.30$
And mole fraction of liquid B = 0.70
Page - 23
Question 1.9 Vapour pressure of pure water at $298 \; K$ is $23.8\; mm \; Hg.$ $50\; g$ of urea $(NH_{2}CONH_{2})$ is dissolved in $850 \; g$ of water. Calculate the vapour pressure of water for this solution and its relative lowering.
Answer :
Given that vapour pressure of pure water, $p^{\circ}_w = 23.8\ mm\ of\ Hg$
Moles of water :
$= \frac{850}{18} = 47.22$
Moles of urea :
$= \frac{50}{60} = 0.83$
Let the vapour pressure of water be Pw.
By Raoult's law, we get :
$\frac{p^{\circ}_w - p_w}{p^{\circ}_w} = \frac{n_2}{n_1\ + n_2}$
or $\frac{23.8 - p_w}{23.8} = \frac{0.83}{47.22\ + 0.83}=0.0173$
or p w = 23.4 mm of Hg.
Relative lowering :- Hence, the vapour pressure(v.P) of water in the solution = 23.4 mm of Hg
and its relative lowering = 0.0173.
Answer :
Here we will use the formula :
$\Delta T_b = \frac{K_b\times1000\times w_2}{M_2\times w_1}$
Elevation in temperature = 100 - 99.63 = 0.37
K b = 0.52 ; $Molar\ mass\ of\ sucrose = 11(12) + 22(1) + 11(16) = 342\ g\ mol^{-1}$
Putting all values in above formula, we get :
$w_2 = \frac{0.37\times342\times500}{0.52\times1000}= 121.67\ g$
Thus 121.67 g of sucrose needs to be added.
Answer :
Elevation in melting point = 1.5 degree celsius.
Here we will use the following equation :
$\Delta T_b = \frac{K_b\times 1000\times w_2}{M_2\times w_1}$
Putting given values in the above equation :
$w_2 = \frac{1.5\times176\times75}{3.9\times1000} = 5.08\ g$
Thus 5.08 ascorbic acid is needed for required condition.
Answer :
We know that :
$Osmotic\ Pressure = \Pi = \frac{n}{v}RT$
We are given with :-
$Moles\ of\ polymer = \frac{1}{185000}$
Volume, V = 0.45 L
Thus osmotic pressure :
$= \frac{\frac{1}{185000}\times8.314\times10^3\times310}{0.45} = 30.98\ Pa$
NCERT Solutions for Class 12 Chemistry Chapter 1 (Exercise Questions)
Here are detailed and accurate NCERT solutions for Exercise Questions of Class 12 Chemistry Chapter 1. These solutions will help in better concept clarity and exam preparation.
Question.1.1 Define the term solution. How many types of solutions are formed? Write briefly about each type with an example.
Answer :
A solution is a homogeneous mixture of two or more non-reacting substances. It has two components :- solute and solvent.
Types of solutions are given below :-
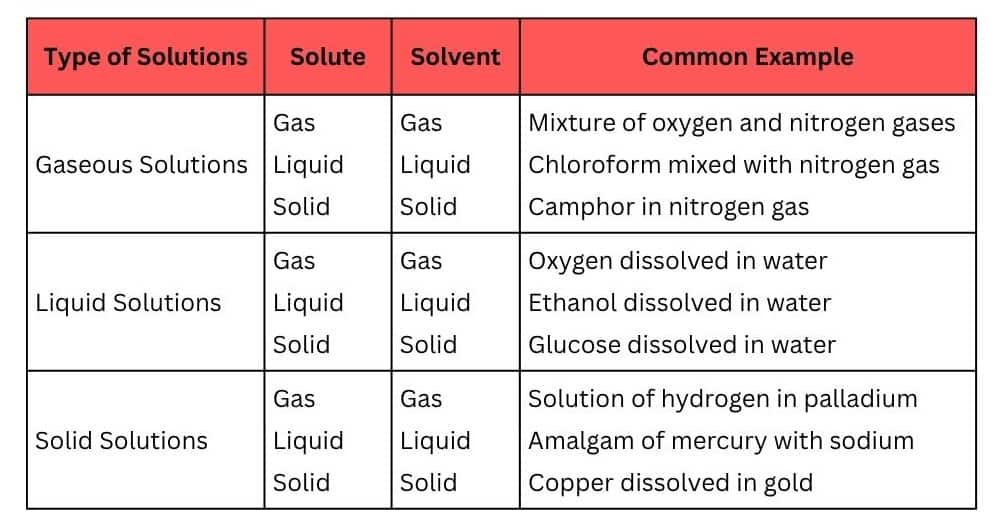
Question 1.2 Give an example of a solid solution in which the solute is a gas.
Answer:
Solution of hydrogen in palladium is such an example in which the solute is a gas and the solvent is a solid.
Question 1.3(i) Define the following terms:
Mole fraction
Answer :
Mole fraction is defined as the ratio of a number of moles of a component to and total number of moles in all components.
i.e., $Mole\ fraction = \frac{Number\ of\ moles\ in\ a\ component }{Total\ number\ of\ moles\ in\ all\ components}$
Question 1.3(ii) Define the following terms:
Molality
Answer :
It is defined as the number of moles of solute dissolved per kg (1000g) of solvent
i.e., $Molality = \frac{Number\ of\ moles\ of\ solute}{Mass\ of\ solvent\ in\ Kg}$
It is independent of temperature.
Question 1.3(iii) Define the following terms:
Molarity
Answer :
Molarity is defined as a number of moles of solute dissolved per litre(or 1000 mL) of solution.
i.e., $Molarity = \frac{No.\ of\ moles\ of\ solute}{Volume\ of\ solution\ in\ litre}$
It depends on temperature because volume is dependent on temperature.
Question 1.3(iv) Define the following terms:
Mass percentage.
Answer :
Mass percentage is defined as the percentage ratio of mass of one component to the total mass of all the components.
i.e., $Mass\ percentage = \frac{Mass\ of\ a\ component}{Total\ mass\ of\ solution}\times100$
Answer :
According to given question, in 100 g of solution 68 g is nitric acid and rest is water.
So moles of 68 g HNO3:-
$=\frac{68}{63}$
= 1.08
Density of solution is given to be 1.504.
So volume of 100 g solution becomes :-
$=\frac{100}{1.504}$
= 66.49\ mL
Thus, molarity of nitric acid is :
Molarity $=\frac{1.08}{\frac{66.49}{1000}}$
= 16.24 M
Answer :
According to question, $10\%$ mass percentage means in 100 g of solution 10 g glucose is dissolved in 90 g water.
Molar mass of glucose (C6H12O6) = $180\ g\ mol^{-1}$
So moles of glucose are :
$\frac{10}{180} = 0.056 mol$
$Moles\: of\: water = \frac{90}{18} = 5 mol$
$Molality = \frac{0.056}{0.09} = 0.62\ m$
Mole fraction :-
$\frac{0.056}{0.056+5} = 0.011$
Molarity :- Volume of 100 g solution :
$=\frac{100}{1.2} =83.3\ mL$
$Molarity = \frac{0.056}{83.33\times10^{-3}} =0.67\ M$
Answer :
Total amount of mixture of Na2CO3 and NaHCO3= 1 g.
Let the amount of Na2CO3 be x g.
So the amount of NaHCO3 will be equal to (1 - x) g.
$Molar\ mass\ of\ Na_2CO_3 = 106\ ;\ molar\ mass\ of\ NaHCO_3 = 84$
Now it is given that it is an equimolar mixture.
So, Moles of Na2CO3= Moles of NaHCO3
or $\frac{x}{106} = \frac{1-x}{84}$
or x = 0.558 g
So $Moles\ of \ Na_2CO_3 = \frac{0.558}{106} = 0.00526$
and $Moles\ of \ NaHCO_3 = \frac{1 - 0.558}{84} = 0.0053$
$\begin{gathered}2 \mathrm{HCl}(a q)+\mathrm{Na}_2 \mathrm{CO}_3(a q) \longrightarrow \mathrm{H}_2 \mathrm{O}(t)+\mathrm{CO}_2(g)+2 \mathrm{NaCl}(a q) \\ \mathrm{NaHCO}_3+\mathrm{HCl} \longrightarrow \mathrm{NaCl}+\mathrm{H}_2 \mathrm{CO}_3\end{gathered}$
It is clear that for 1 mol of Na2CO3 2 mol of HCl is required, similarly for 1 mol of NaHCO3 1 mol of HCl is required.
So number of moles required of HCl = 2(0.00526) + 0.0053 = 0.01578 mol
It is given that molarity of HCl is 0.1 which means 0.1 mol of HCl in 1 L of solution.
Thus required volume :
$= \frac{0.01578}{0.1} = 0.1578\ l = 157.8\ mL$
Answer :
According to question we have 2 solute,
Solute 1. : $25\%$ of 300 g gives :
$\frac{25}{100}\times300 = 75\ g$
Solute 2. : $40\%$ of 400 g gives :
$\frac{40}{100}\times400 = 160\ g$
So total amount of solute = 75 + 160 = 235 g.
Thus mass percentage of solute is :
$= \frac{235}{700}\times100 = 33.5\%$
and mass percentage of water $= 100 - 33.5 = 66.5\%$
Answer :
For finding molality we need to find the moles of ethylene glycol.
Moles of ethylene glycol :
$= \frac{222.6}{62}= 3.59\ mol$
We know that :
$Molality = \frac{Moles\ of\ ethylene\ glycol}{Mass\ of\ water}\times100$
$= \frac{3.59}{200}\times100 = 17.95\ m$
Now for molarity :-
Total mass of solution = 200 + 222.6 = 422.6 g
Volume of solution
$= \frac{422.6}{1.072}= 394.22\ mL$
So molarity :-
$= \frac{3.59}{394.22}\times1000= 9.11\ M$
express this in percent by mass
Answer :
We know that 15 ppm means 15 parts per million.
Required percent by mass :
$= \frac{Mass\ of\ chlorofoam}{Total\ mass}\times100$
$= \frac{15}{10^6}\times100 = 1.5\times10^{-3}\%$
determine the molality of chloroform in the water sample.
Answer :
Moles of chloroform :
$=\frac{15}{119.5} = 0.1255\ mol$
Mass of water is $10^6$ . (Since contamination is 15 ppm)
So molality will be :
$=\frac{0.1255}{10^6}\times1000 = 1.255\times10^{-4}\ m$
Question 1.10 What role does the molecular interaction play in a solution of alcohol and water?
Answer :
Both alcohol and water individually have strong hydrogen bonds as their force of attraction. When we mix alcohol with water they form solution due to the formation of hydrogen bonds but they are weaker as compared to hydrogen bonds of pure water or pure alcohol.
Thus this solution shows a positive deviation from the ideal behaviour.
Question 1.11 Why do gases always tend to be less soluble in liquids as the temperature is raised?
Answer:
It is known that dissolution of gas in a liquid is an exothermic process. So, by Le Chatelier principle we know that equilibrium shifts backwards as we increase temperature in case of exothermic process. Thus gases always tend to be less soluble in liquids as the temperature is raised.
Question 1.12 State Henry’s law and mention some important applications.
Answer :
According to Henry's law at a constant temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas present above the surface of the solution or liquid.
i.e., p = kh.x, Here kh is Henry’s law constant.
Some of its applications are as follows:-
(a) We can increase the solubility of CO2 in soft drinks, the bottle is sealed under high pressure.
(b) To avoid bends (due to blockage of capillaries) and the toxic effects of high concentrations of nitrogen in the blood, the tanks used by scuba divers are filled with air diluted with helium (11.7% helium, 56.2% nitrogen and 32.1% oxygen).
(c) The partial pressure of oxygen is less at high altitudes than at ground level. This leads to low concentrations of oxygen in the blood and tissues, climbers. Due to low blood oxygen, climbers become weak and unable to think clearly, which are symptoms of a condition known as anoxia.
Answer :
Using Henry's Law we can write,
$m = k.P$
Putting value in this equation, we get :
$6.56\times10^{-3} = k\times 1$
So, the magnitude of k is $6.56\times10^{-3}$ .
Now, we will again use the above equation for $m = 5.0\times10^{-2}\ g$ .
So the required partial pressure is :-
$p = \frac{m}{k} = \frac{5.0\times10^{-2}}{6.56\times10^{-3}}$
or $p = 7.62\ bar$
Answer :
Positive and negative deviation: - A non-ideal solution is defined as a solution which does not obey Raoult’s law over the entire range of concentration i.e., $\Delta _{Mix}H \neq 0$ and $\Delta _{Mix}V \neq 0$ . The vapour pressure of these solutions is either higher or lower than that expected by Raoult’s law. If vapour pressure is higher, the solution shows a positive deviation and if it is lower, it shows a negative deviation from Raoult’s law.
Enthalpy relation to positive and negative deviation can be understood from the following example:-
Consider a solution made up of two components - A and B. In the pure state the intermolecular force of attraction between them are A-A and B-B. But when we mix the two, we get a binary solution with molecular interaction A-B.
If A-B interaction is weak than A-A and B-B then enthalpy of reaction will be positive thus reaction will tend to move in a backward direction. Hence molecules in binary solution will have a higher tendency to escape. Thus vapour pressure increases and shows positive deviation from the ideal behaviour.
Similarly, for negative deviation, A-B interaction is stronger than that of A-A and B-B.
Answer :
It is given that $2\%$ of aq. solution. This means 2 g of non-volatile solute in 98 g of H 2 O.
Also the vapour of water at normal boiling point = 1.013 bar.
Using Raoult's law :
$\frac{p_w^{\circ} - p}{p_w^{\circ}} = \frac{w_2.M_1}{w_1.M_2}$
So we get :
$M_2 = \frac{2\times18\times1.013}{0.009\times98} = 41.35\ g\ mol^{-1}$
Thus, the molar mass of non-volatile solute is 41.35 units.
Answer :
Vapour pressure of heptane = $p_h^{\circ} = 105.2\ KPa$
and vapour pressure of octane = $p_o^{\circ} = 46.8\ KPa$
Firstly, we will find moles of heptane and octane so that we can find the vapour pressure of each.
Molar mass of heptane = 7(12) + 16(1) = 100 unit.
and molar mass of octane = 8(12) + 18(1) = 114 unit.
So moles of heptane :
$\frac{26}{100} = 0.26$
and moles of octane :
$\frac{35}{114} = 0.31$
Mole fraction of heptane = 0.456 and mole fraction of octane = 0.544
Now we will find the partial vapour pressure:-
(i) of heptane :- $p_h = 0.456\times105.2 = 47.97\ KPa$
(ii) of octane :- $p_o = 0.544\times46.8 = 25.46\ KPa$
So total pressure of solution = $p_h+p_o$
= 47.97 + 25.46 = 73.43 KPa
Answer :
It is asked the vapour pressure of a 1 molal solution, which means 1 mol of solute in 1000 g H 2 O.
Moles in 1000g of water = 55.55 mol. (Since the molecular weight of H 2 O is 18)
Mole fraction of solute :
$\frac{1}{1+55.55} = 0.0177$
Applying the equation :
$\frac{p_w^{\circ} - p}{p_w^{\circ}} = x_2$
or $\frac{12.3 - p}{12.3} = 0.0177$
or $p = 12.083\ KPa$
Thus the vapour pressure of the solution is 12.083 KPa
Answer :
Let the initial vapour pressure of octane = $p_o^{\circ}$.
After adding solute to octane, the vapour pressure becomes :
$=\frac{80}{100}\times p_o^{\circ} = 0.8p_o^{\circ}$
Moles of octane :
$= \frac{114}{114} = 1$ $\left ( Molar\ mass\ of\ octane = 8(12) + 18(1) = 114\ g\ mol^{-1} \right )$
Using Raoult's law we get :
$\frac{p_o^{\circ} - p}{p_o^{\circ}} = x_2$
or $\frac{p_o^{\circ} -0.8p_o^{\circ} }{p_o^{\circ}} = \frac{\frac{W}{40}}{\frac{W}{40}+1}$
or $w = 10\ g$
Thus required mass of non-volatile solute = 10g.
the molar mass of the solute
Answer :
In this question, we will find the molar mass of the solute by using Raoult's law.
Let the molar mass of the solute be M.
Initially, we had 30 g of solute and 90 g of water.
Moles of water :
$\frac{90}{18} = 5\ mol$
By Raoult's law we have:-
$\frac{p_w^{\circ} - p}{p_w^{\circ}} = \frac{n_2}{n_1+n_2}$
or $\frac{p_w^{\circ} - 2.8}{p_w^{\circ}} = \frac{\frac{30}{M}}{5+\frac{30}{M}} = \frac{30}{5M+30}$
or $\frac{p_w^{\circ} }{2.8} = \frac{5M+30}{5M}$ ------------------------------ (i)
Now we have added 18 g of water more, so the equation becomes:
Moles of H2O :
$\frac{90+18}{18} = 6\ mol$
Putting this in above equation we obtain:-
$\frac{p_w^{\circ} - 2.9}{p_w^{\circ}} = \frac{\frac{30}{M}}{6+\frac{30}{M}} = \frac{30}{6M+30}$
or $\frac{p_w^{\circ} }{2.9} = \frac{6M +30}{6M}$ -----------------------------------(ii)
From equation (i) and (ii) we get
M = 23 u
So the molar mass of solute is 23 units.
vapour pressure of water at 298 K.
Answer :
In the previous part we have calculated the value of molar mass the Raoul's law equation.
We had :-
$\frac{p_w^{\circ} }{2.8} = \frac{5M+30}{5M}$
Putting M = 23 u in the above equation we get,
$\frac{p_w^{\circ} }{2.8} = \frac{5(23)+30}{5(23) } =\frac{145}{115}$
or $p_w^{\circ} =3.53$
Thus vapour pressure of water = 3.53 kPa.
Answer :
It is given that the freezing point of pure water is 273.15 K.
So, elevation of freezing point = 273.15 - 271 = 2.15 K
$5\%$ solution means 5 g solute in 95 g of water.
Moles of cane sugar :
$= \frac{5}{342} = 0.0146$
Molality :
$= \frac{0.0146}{0.095} = 0.1537$
We also know that - $\Delta T_f = k_f \times m$
or $k_f = \frac{\Delta T_f}{m} = 13.99\ K\ Kg\ mol^{-1}$
Now we will use the above procedure for glucose.
$5\%$ of glucose means 5 g of gluocse in 95 g of H 2 O.
Moles of glucose :
$\frac{5}{180} = 0.0278$
Thus molality :
$= \frac{.0278}{0.095} = 0.2926\ mol\ kg^{-1}$
So, we can find the elevation in freezing point:
$\Delta T_f = k_f \times m$
$= 13.99 \times 0.2926 = 4.09\ K$
Thus freezing point of glucose solution is 273.15 - 4.09 = 269.06 K.
Answer :
In this question we will use the formula :
$\Delta T_f = k_f \times m$
Firstly for compound AB2 :-
$M_B = \frac{K_f\times W_b \times 1000}{w_A\times \Delta T_f}$
or $= \frac{5.1\times 1 \times 1000}{20\times 2.3} = 110.87\ g/mol$
Similarly for compound AB4 :-
$M_B= \frac{5.1\times 1 \times 1000}{20\times 1.3} = 196\ g/mol$
If we assume atomic weight of element A to be x and of element B to be y, then we have :-
x + 2y = 110.87 ----------------- (i)
x + 4y = 196 ----------------- (ii)
Solving both the equations, we get :-
x = 25.59 ; y = 42.6
Hence atomic mass of element A is 25.59u and atomic mass of element B is 42.6u.
Answer :
According to given conditions we have same solution under same temperature. So we can write :
$\frac{\Pi _1}{C_1} = \frac{\Pi _2}{C_2}$ $\left ( \Pi = C.R.T\ ; RT = \frac{\Pi }{C} \right )$
So, if we put all the given values in above equation, we get
$\frac{4.98}{\frac{36}{180}} = \frac{1.52}{C_2}$
or $C_2 = \frac{1.52\times36}{4.98\times180} = 0.061 M$
Hence the required concentration is 0.061 M.
Question 1.23(i) Suggest the most important type of intermolecular attractive interaction in the following pairs.
n-hexane and n-octane
Answer :
Since both the compounds are alkanes so their mixture has van der Waal force of attraction between compounds.
Question 1.23(ii) Suggest the most important type of intermolecular attractive interaction in the following pairs.
Answer :
The binary mixture of these compounds has van der Waal force of attraction between them.
Question 1.23(iii) Suggest the most important type of intermolecular attractive interaction in the following pairs.
Answer :
The given compounds will have ion-dipole interaction between them.
Question 1.23(iv) Suggest the most important type of intermolecular attractive interaction in the following pairs.
Answer :
Methanol has -OH group and acetone has ketone group. So there will be hydrogen bonding between them.
Question 1.23(v) Suggest the most important type of intermolecular attractive interaction in the following pairs.
acetonitrile $(CH_{3}CN)$ and acetone $(C_{3}H_{6}O).$
Answer :
They will have dipole-dipole interaction since both are polar compounds.
Question 1.24 Based on solute-solvent interactions, arrange the following in order of increasing solubility in n-octane and explain.
Cyclohexane, KCl, CH3OH, CH3CN.
Answer :
The order will be : Cyclohexane > CH3CN > CH3OH > KCl
In this, we have used the fact that like dissolves like.
Since cyclohexane is an alkane so its solubility will be maximum.
Question 1.25(i) Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
phenol
Answer :
We know the fact that like dissolves in like.
Since phenol is had both polar and non-polar group so it is partially soluble in water.
Question 1.25(ii) Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
toluene
Answer :
Since toluene is a non-polar compound i.e., it doesn't have any polar group so it is insoluble in water. (because water is a polar compound)
Question 1.25(iii) Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
formic acid
Answer :
Since the -OH group in formic acid (polar) can form H-bonds with water thus it is highly soluble in water.
Question 1.25(iv) Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
ethylene glycol
Answer :
Ethylene glycol is an organic compound but is polar in nature. Also, it can form H-bonds with water molecules, thus it is highly soluble in water.
Question 1.25(v) Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
chloroform
Answer :
Chloroform is a non-polar compound so it is insoluble in water.
Question 1.25(vi) Amongst the following compounds, identify which are insoluble, partially soluble and highly soluble in water?
pentanol
Answer :
Pentanol has both polar and non-polar groups so it is partially soluble in water.
Answer :
We know that, Molality :
$Molality = \frac{Moles\ of\ solute}{Mass\ of\ solvent\ in\ Kg}$
So, for moles of solute we have :
$Moles\ of\ Na^+ = \frac{92}{23} = 4$
Thus, molality :
$= \frac{4}{1} = 4$
Molality of Na + ions is 4m.
Question 1.27 If the solubility product of $CuS$ is $6\times10^{-16}$ , calculate the maximum molarity of $CuS$ in aqueous solution.
Answer :
We are given, $K_{sp} = 6\times10^{-16}$
The dissociation equation of CuS is given by :-
$\mathrm{CuS} \rightleftharpoons \mathrm{Cu}^{2+}+\mathrm{S}^{2-}$
So, the equation becomes :- $K_{sp} = Cu^{2+}\times {S^{2-}}$
or $K_{sp} = s\times s = s^2$
or $s = 2.45\times 10^{-8}\ M$
Thus maximum molarity of solution is $2.45\times 10^{-8}\ M$ .
Answer :
Total mass of solution = Mass of aspirin + Mass of acetonitrile = 6.5 + 450 = 456.5 g.
We know that :
$Mass\ percentage = \frac{Mass\ of\ solute }{Mass\ of\ solution}\times100$
So, $Mass\ percentage = \frac{6.5 }{456.5}\times100 = 1.42\%$
Thus the mass percentage of aspirin is $1.42\%$
Answer :
We are given with molality of the solution, so we need to find the moles of Nalorphene.
Molar mass of nalorphene = 19(12) + 21(1) + 1(14) + 3(16) = 311u.
So moles of nalorphene :
$\frac{1.5\times10^{-3}}{311} = 4.82\times 10^{-6}\ moles$
Molality :
$= \frac{No.\ of\ moles\ of\ solute}{Mass\ of\ solvent\ in\ kg}$
or $1.5\times 10^{-3} = \frac{4.82\times 10^{-6}}{w}$
or $w = 3.2\times 10^{-3}\ Kg$
So the required weight of water is 3.2 g.
Question 1.30 Calculate the amount of benzoic acid $(C_{6}H_{5}COOH)$ required for preparing $250\; mL$ of $0.15 \; M$ solution in methanol.
Answer :
Molar mass of benzoic acid = 7(12) + 6(1) + 2(16) = 122u.
We are given with the molarity of a solution.
$Molarity = \frac{Moles\ of\ solute}{Volume\ of\ solution\ in\ litre}$
or $0.15 = \frac{Moles\ of\ solute}{\frac{250}{1000}}$
or $Moles\ of\ solute= \frac{0.15\times 250}{1000} = 0.0375\ mol$
So mass of benzoic acid :
$= Moles\ of\ benzoic\ acid \times Molar\ mass$
$=0.0375\times 122 = 4.575\ g$
Hence the required amount of benzoic acid is 4.575 g.
Answer :
We know that depression in the freezing point of water will depend upon the degree of ionisation.
The degree of ionisation will be highest in the case of trifluoroacetic acid as it is most acidic among all three.
The order of degree of ionisation on the basis if acidic nature will be:- Trifluoroacetic acid > Trichloroacetic acid > Acetic acid.
So the depression in freezing point will be reverse of the above order.
$K_{a}=1.4\times 10^{-3}$ , $K_{f}=1.86\; K\; kg\; mol^{-1}$
Answer :
Firstly we will find the Vant's Hoff factor the dissociation of given compound.
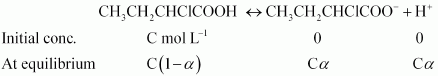
So we can write, $K_a = \frac{(Ca\times Ca)}{C(1-a)}$
or $K_a = Ca^2$ $(\because a << 1)$
or $a = \sqrt{\frac{K_a}{C}}$
Putting values of K a and C in the last result, we get :
$a = 0.0655$
At equilibrium i = 1 - a + a + a = 1 + a = 1.0655
Now we need to find the moles of the given compound CH3 CH2CHClCOOH.
So, moles =
$\frac{10}{122.5} = 0.0816\ mol$
Thus, molality of the solution :
$= \frac{0.0816\times1000}{250} = 0.3265\ m$
Now we will use :
$\Delta T_f = i\ K_f\ m$
or $= 1.065 \times 1.86 \times 0.3265 = 0.6467\ K$
Answer :
Firstly we need to calculate molality in order to get vant's hoff factor.
So moles of CH2FCOOH :
$\frac{19.5}{78} = 0.25$
We need to assume volume of solution to be nearly equal to 500 mL. (as 500 g water is present)
Now, we know that : $\Delta T_f = i\ K_f\ m$
or $i = \frac{1}{0.93} = 1.0753$
Now for dissociation constant :-
$a = i - 1 = 1.0753 - 1 = 0.0753$
and, $K_a = \frac{Ca^2}{1-a}$
Put values of C and a in the above equation, we get :
$K_a = 3\times10^{-3}$
Answer :
Firstly we will find number of moles of both water and glucose.
Moles of glucose :
$= \frac{25}{180} = 0.139\ mol$ $(Molar\ mass\ of\ glucose = 6(12)+12(1)+6(16) = 180\ g\ mol^{-1})$
and moles of water :
$= \frac{450}{18} = 25\ mol$ $(Molar\ mass\ of\ water = 18\ g\ mol^{-1})$
Now,
$\frac{p_w^{\circ} - p}{p_w^{\circ}} = \frac{n_g}{n_g + n_w}$
or $\frac{17.535 - p}{17.535} = \frac{0.139}{0.139+ 25}$
or $p = 17.44\ mm\ of\ Hg$
Thus vapour pressure of water after glucose addition = 17.44 mm of Hg
Answer :
We know that : $P = k\times C$
We are given value of P and k, so C can be found.
$C = \frac{760}{4.27\times10^5} = 178\times 10^{-5}$
Hence solubility of methane in benzene is $178\times 10^{-5}$ .
Answer :
For calculating partial vapour pressure we need to calculate mole fractions of components.
So number of moles of liquid A :
$= \frac{100}{140} = 0.714$
and moles of liquid B :
$= \frac{1000}{180} = 5.556$
Mole fraction of A (x A ) :
$= \frac{0.714}{0.714+5.556} = 0.114$
and mole fraction of B (x B ) :
$= \frac{5.556}{0.714+5.556} = 0.866$
Now, P total = P A + P B
or $P_{total} = P_A^{\circ}x_A\ + P_B^{\circ}x_B$
or $475 = P_A^{\circ}\times0.114\ + 500\times0.886$
or $P_A^{\circ} = 280.7\ torr$
Thus vapour pressure in solution due to A = $P_A^{\circ}x_A$
$= 280.7 \times0.114 = 32\ torr$
Plot this data also on the same graph paper. Indicate whether it has positive deviation or negative deviation from the ideal solution.
Answer :
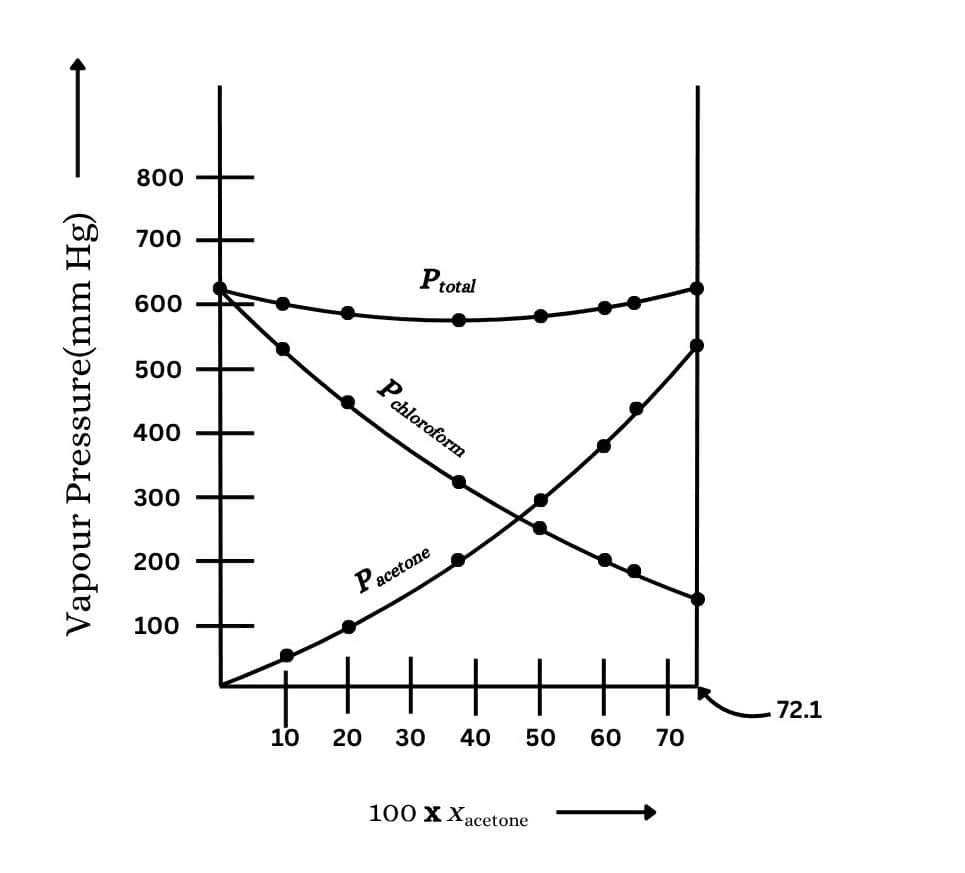
it has negative deviation from the ideal solution.
Answer :
Firstly, we will find the no. of moles of the given compounds.
No. of moles of benzene :
$=\frac{80}{78} = 1.026\ mol$
and the no. of moles of toluene :
$=\frac{100}{92} = 1.087\ mol$ .
Now we will find mol fraction of both:-
Mole fraction of benzene :-
$=\frac{1.026}{1.026+1.087} = 0.486$
and mole fraction of toluene :
$=1 - 0.486 = 0.514$
Now,
P total = Pb + Pt
or $= 50.71\times0.486\ + 32.06\times0.514\ = 24.65 +16.48$
or $= 41.13\ mm\ of\ Hg$
Hence mole fraction of benzene in vapour phase is given by :
$= \frac{24.65}{41.13} = 0.60$
Answer :
We have been given that the water is in equilibrium with air at a pressure of 10 atm or 7600 mm of Hg.
So the partial pressure of oxygen :
$\frac{20}{100}\times7600 = 1520\ mm\ of\ Hg$
and partial pressure of nitrogen :
$\frac{79}{100}\times7600 = 6004\ mm\ of\ Hg$
Now, by Henry's Law :
$P = K_h.x$
For oxygen :
$x = \frac{1520}{3.30\times10^{7}} = 4.61\times 10^{-5}$
For nitrogen :
$x = \frac{6004}{6.51\times10^{7}} = 9.22\times 10^{-5}$
Hence the mole fraction of nitrogen and oxygen in water is $9.22\times 10^{-5}$ and $4.61\times 10^{-5}$ respectively.
Answer :
We know that osmotic pressure :
$\Pi = i\ (\frac{n}{v})\ R\ T$
or $\Pi = i\ (\frac{w}{M\ v})\ R\ T$
We have been given the values of osmotic pressure, V, i and T.
So the value of w can be found.
$w = \frac{0.75\times111\times2.5}{2.47\times0.0821\times300}$ $(M = 1\times40 + 2\times 35.5 = 111\ g\ mol^{-1})$
$= 3.42\ g$
Hence 3.42 g CaCl2 is required.
Answer :
Dissociation of K 2 SO 4 is as follows :-
$\mathrm{K}_2 \mathrm{SO}_{4(\mathrm{~s})} \rightarrow 2 \mathrm{~K}_{(\mathrm{aq})}^{+}+\mathrm{SO}_4{ }^{2-}{ }_{(\mathrm{aq})}$ It is clear that 3 ions are produced, so the value of i will be 3.
Molecular weight of K 2 SO 4 = 2(39) + 1(32) + 4(16) = 174u.
$\Pi = i\ C\ R\ T$
Putting all the values :-
$\Pi =\frac{3 \times 25 \times 10-3 \times 0.082 \times 298}{174\times2}$
$= 5.27\times10^{-3}\ atm$
Class 12 Chemistry NCERT Chapter 1: Higher Order Thinking Skills (HOTS) Questions
These HOTS class 12 chemistry chapter 1 solutions question answer are designed to test students understanding and application of concepts. These NCERT Solutions help in developing critical thinking skills and prepare students for complex questions in competitive exams.
Question 1. $\mathrm{HA}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{A}^{-}(\mathrm{aq})$
The freezing point depression of a 0.1 m aqueous solution of a monobasic weak acid HA is $0.20^{\circ} \mathrm{C}$. The dissociation constant for the acid is
Given :
$\mathrm{K}_{\mathrm{f}}\left(\mathrm{H}_2 \mathrm{O}\right)=1.8 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$, molality $\equiv$ molarity
(1). $1.38 \times 10^{-3}$
(2). $1.1 \times 10^{-2}$
(3). $1.90 \times 10^{-3}$
(4). $1.89 \times 10^{-1}$
Answer:
$\begin{aligned} & \Delta \mathrm{T}_{\mathrm{f}}=\mathrm{i} \mathrm{K}_{\mathrm{f}} \mathrm{m} \\ & \mathrm{i}=\frac{\Delta \mathrm{T}_f}{\mathrm{~K}_{\mathrm{f}} \cdot \mathrm{m}} \\ & \mathrm{i}=\frac{0.20}{1.8 \times 0.1}=1.11 \\ & \mathrm{i}=1.11 \\ & \alpha=\frac{i-1}{\mathrm{n}-1}(\text { for } \mathrm{HA}, \mathrm{n}=2) \\ & \alpha=\frac{1.11-1}{1}=0.11 \\ & \mathrm{~K}_{\mathrm{a}}=\frac{c \alpha^2}{1-\alpha}=\frac{0.1 \times(0.11)^2}{1-0.11}=1.38 \times 10^{-3}\end{aligned}$
Hence, the correct answer is option (1).
Question 2. Which of the following binary mixture does not show the behaviour of minimum boiling azeotropes ?
(1) $\mathrm{H}_2 \mathrm{O}+\mathrm{CH}_3 \mathrm{COC}_2 \mathrm{H}_5$
(2) $\mathrm{C}_6 \mathrm{H}_5 \mathrm{OH}+\mathrm{C}_6 \mathrm{H}_5 \mathrm{NH}_2$
(3) $\mathrm{CS}_2+\mathrm{CH}_3 \mathrm{COCH}_3$
(4) $\mathrm{CH}_3 \mathrm{OH}+\mathrm{CHCl}_3$
Answer:
The solution showing positive deviation from Raoult's law will form a minimum boiling azeotrope. Phenol + Aniline shows negative deviation, so they will not form a minimum boiling azeotrope.
A binary mixture of $\mathrm{C}_6 \mathrm{H}_5 \mathrm{OH}$ and $\mathrm{C}_6 \mathrm{H}_5 \mathrm{NH}_2$ exhibits negative deviation from Raoult's law. This means that the vapor pressure of the solution is lower than the vapor pressures of the pure components, $\mathrm{C}_6 \mathrm{H}_5 \mathrm{OH}$ and $\mathrm{C}_6 \mathrm{H}_5 \mathrm{NH}_2$. Consequently, the boiling point of the solution is higher than the boiling points of the pure substances. Therefore, this mixture forms a maximum boiling azeotrope.
Hence, the correct answer is option (2).
Question 3. Given below are two statements :
Statement (I) : Molal depression constant $\mathrm{K}_{\mathrm{f}}$ is given by $\frac{M_1 R T_f}{\Delta S_{f u s}}$, where symbols have their usual meaning.
Statement (II) : $\mathrm{K}_{\mathrm{f}}$ for benzene is less than the $\mathrm{K}_f$ for water.
In the light of the above statements, choose the most appropriate answer from the options given below :
(1) Statement I is incorrect but Statement II is correct
(2) Both Statement I and Statement II are incorrect
(3) Both Statement I and Statement II are correct
(4) Statement I is correct but Statement II is incorrect
Answer:
Statement-I
Molar depression constant $\mathrm{k}_f=\frac{\mathrm{M}_{\mathrm{i}} \mathrm{RT}_{\mathrm{f}}^2}{\Delta \mathrm{H}_{\text {fius }}}$
$\begin{aligned}
& \mathrm{k}_f=\frac{\mathrm{M}_1 \mathrm{RT}_{\mathrm{f}}}{\left[\frac{\Delta \mathrm{H}_{\text {fis }}}{\mathrm{T}_{\mathrm{f}}}\right]} \\
& \mathrm{k}_f=\frac{\mathrm{M}_1 \mathrm{RT}_f}{\Delta \mathrm{~S}_{\text {fus }}}
\end{aligned}$
Hence statement-I is correct
but $\mathrm{k}_{\mathrm{f}}$ for benzene $=5.12 \frac{{ }^{\circ} \mathrm{C}}{\text { molal }}$
$\mathrm{k}_{\mathrm{f}}$ for water $=1.86 \frac{{ }^{\circ} \mathrm{C}}{\text { molal }}$ Hence statement- II is incorrect
Hence, the correct answer is option (4).
Question 4. 20 mL of sodium iodide solution gave 4.74 g silver iodide when treated with excess of silver nitrate solution. The molarity of the sodium iodide solution is ________ M. (Nearest Integer value)
(Given : $\mathrm{Na}=23, \mathrm{I}=127, \mathrm{Ag}=108, \mathrm{~N}=14$, $\left.\mathrm{O}=16 \mathrm{~g} \mathrm{~mol}^{-1}\right)$
Answer:
Let molarity of Nal solution be $\times \mathrm{M}$
$\mathrm{NaI}+\mathrm{AgNO}_3 \rightarrow \mathrm{AgI}+\mathrm{NaNO}_3$
This is a 1:1 molar reaction — 1 mole of NaI gives 1 mole of AgI.
Moles of AgI $=\frac{4.74}{235} \approx 0.02017 \mathrm{~mol}$
So, moles of Nal = moles of Agl = $\mathbf{0 . 0 2 0 1 7 ~ m o l}$
Step 3: Use molarity formula
$$
\text { Molarity }=\frac{\text { moles }}{\text { volume in } \mathrm{L}}=\frac{0.02017}{0.020} \approx 1.0085 \mathrm{M}
$$
Hence, the answer is 1.
Question 5. Liquid A and B form an ideal solution. The vapour pressure of pure liquids A and B are 350 and 750 mm Hg respectively at the same temperature. If $\mathrm{x}_{\mathrm{A}}$ and $x_B$ are the mole fraction of $A$ and $B$ in solution while $y_A$ and $y_B$ are the mole fraction of $A$ and $B$ in vapour phase then :
(1) $\frac{x_A}{x_B}<\frac{y_A}{y_B}$
(2) $\frac{x_A}{x_B}=\frac{y_A}{y_B}$
(3) $\frac{x_A}{x_B}>\frac{y_A}{y_B}$
(4) $\left(\mathrm{x}_{\mathrm{A}}-\mathrm{y}_{\mathrm{A}}\right)<\left(\mathrm{x}_{\mathrm{B}}-\mathrm{y}_{\mathrm{B}}\right)$
Answer:
$\begin{array}{ll}P_A^0=350 \mathrm{~mm} \mathrm{Hg} & \mathrm{P}_B^0=750 \mathrm{~mm} \mathrm{Hg} \\ \mathrm{y}_A=\frac{350 \mathrm{x}_A}{\mathrm{P}_{\mathrm{T}}} & \mathrm{y}_B=\frac{350 \mathrm{x}_B}{\mathrm{P}_{\mathrm{T}}}\end{array}$
$\begin{aligned} & \frac{y_A}{y_B}=\frac{350 x_A}{750 x_B} \\ & \Rightarrow \frac{y_A}{y_B}<\frac{x_A}{x_B}\end{aligned}$
Hence, the correct answer is option (3).
CBSE Class 12th Syllabus: Subjects & Chapters
Select your preferred subject to view the chapters
Approaches to Solve Problems of Chapter 1 Chemistry Class 12
Sometimes, problems related to class 12 chemistry chapter 1 solutions seem difficult, but once we understand the basic formulas, it becomes very easy to solve all the questions related to Solutions. We can follow the steps given below to solve the questions based on the Solutions:
1. The first step is to identify the solute and solvent and learn to classify the solution based on the states of components like solid in liquid, gas in liquid, etc. Also, learn to apply the concentration formulas
Molarity (M), Molality (m), Mole fraction (χ), Mass %, Volume %
(i). Molarity
$M=\frac{\text { moles of solute }}{\text { volume of solution in liters }}$
(ii). Molality
$m=\frac{\text { moles of solute }}{\text { mass of solvent in } \mathrm{kg}}$
(iii). Mole Fraction
$X_A=\frac{\text { moles of component } A}{\text { total moles of solution }}$
2. Important formulas from chapter 1 solutions class 12 chemistry are given below. These formulas help students to solve questions easily.
Henry's Law: $P=k_H \cdot x$ for gas solubility.
Raoult's Law- For ideal solutions, use $p_A=x_A \cdot p_A^0$.
Apply to vapor pressure problems.
3. Identify which property is involved ( $\Delta \mathrm{Tf}, \Delta \mathrm{Tb}, \pi, \Delta \mathrm{P}$ ).
Use-
(i). Elevation in Boiling Point : $\Delta T_b=i \cdot K_b \cdot m$
(ii). Depression in Freezing Point: $\Delta T_f=i \cdot K_f \cdot m$
(iii). Osmotic Pressure: $\pi=i \cdot C \cdot R \cdot T$
4. Learn to determine if solute dissociates or associates. Adjust formulas using ? for non-ideal cases.
5. While solving questions from class 12 chemistry chapter 1 solutions the numericals, keep units consistent and understand what each symbol represents. You can also draw diagrams for clarity also focus on ideal vs non-ideal solutions, positive/negative deviations, and azeotropes. Students can also access the NCERT exemplar solutions for better understanding.
Topics of NCERT Syllabus Class 12 Chemistry Solutions
1.2 Expression Of Concentration Of Solution
1.3 Solubility
- 1.3.1 Solubility of a Solid in a Liquid
- 1.3.2 Solubility of a Gas in a Liquid
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook1.4 Vapour Pressure Of Liquid Solutions
- 1.4.1 Vapour Pressure of Liquid-Liquid Solutions
- 1.4.2 Raoult's Law as a special case of Henry's Law
- 1.4.3 Vapour Pressure of Solutions of Solids in Liquids
1.5 Ideal and Non-ideal Solutions
- 1.5.1 Ideal Solutions
- 1.5.2 Non-ideal Solutions
1.6 Colligative Properties and Determination of Molar Mass
- 1.6.1 Relative Lowering of Vapour Pressure
- 1.6.2 Elevation of Boiling Point
- 1.6.3 Depression of Freezing Point
- 1.6.4 Osmosis and Osmotic Pressure
- 1.6.5 Reverse Osmosis and Water Purification
1.7 Abnormal Molar Masses
What Extra Should Students Study Beyond the NCERT for JEE/NEET?
Here a comparison table highlighting what to study beyond NCERT for JEE. While NCERT books build a strong foundation, students should also refer to advanced reference books and practice materials. Solving class 12 chemistry chapter 1 solutions question answer can help strengthen problem-solving skills and improve exam performance.
What Students Learn from NCERT Solutions for Class 12 Chemistry Chapter 1 Solutions
These class 12 chemistry chapter 1 solutions help students understand the key concepts of the solid state in a simple and structured way. Given below some points on key learning from this chapter
- Using these solutions students can understand the fundamental concepts of the solid state.
- Here they can learn about types of solids and their properties.
- Properties like unit cells, crystal lattices, and packing efficiency are explained very well in these solutions class 12 question answer
- These solutions help students to calculate the density and voids in crystals
- Imperfections in solids, coordination number and geometrical arrangements are explained in these solutions very well.
Importance of Class 12 Chemistry Chapter 1 – Solutions
The class 12 chemistry chapter 1 solutions question answer develops the base for understanding the behaviour of mixtures in both laboratory and industrial applications.
- The chapter develops the basic understanding of homogeneous and heterogeneous mixtures.
- Students will learn about concentration terms and their calculations.
- The class 12 chemistry solutions question answer explains how temperature, pressure, and the nature of solute and solvent affect solubility.
- Colligative Properties like relative lowering of vapour pressure, elevation in boiling point, depression in freezing point, and osmotic pressure are discussed here.
NCERT solutions for class 12 chemistry
Along with NCERT Solutions for Class 12 Chemistry Chapter 1 Solutions also refer to chapter-wise solutions for the entire Class 12 Chemistry syllabus:
NCERT Exemplar Class 12 Solutions
The NCERT Exemplar Class 12 solutions provide questions with detailed answers to enhance conceptual understanding. The hyperlinks of NCERT exemplar of class 12 are given below:
NCERT Solutions for Class 12: Other Subjects
Along with NCERT Solutions for Class 12 Chemistry, students can also check solutions for other subjects that are equally important for board exams and competitive exams like JEE and NEET.
NCERT Books and NCERT Syllabus
The NCERT books and syllabus provide a clear and structured framework for learning all subjects. The hyperlinks of the NCERT Books and NCERT syllabus are given below:
Frequently Asked Questions (FAQs)
Q: How to get NCERT solutions for Class 12 chemistry Ch 1?
A:
You can get NCERT solutions for Class 12 Chemistry Chapter 1 from various educational websites and online learning platforms. They are also available as free downloadable PDFs, which can be accessed anytime for easy study and revision.
Q: What are NCERT Solutions for Class 12 Chemistry Chapter 1?
A:
NCERT Solutions for Class 12 Chemistry Chapter 1 are detailed answers to all questions provided in the textbook. They explain concepts of the solid state, crystal structures, and related numerical problems in a simple, step-by-step manner to help students understand and practise effectively for exams.
Q: What are NCERT Solutions for Class 12 Chemistry Chapter 1?
A:
NCERT Solutions for Class 12 Chemistry Chapter 1 are detailed answers to all questions provided in the textbook. They explain concepts of the solid state, crystal structures, and related numerical problems in a simple, step-by-step manner to help students understand and practise effectively for exams.
Q: What is a solution?
A:
A solution is a homogeneous mixture composed of two or more substances. In a solution, a solute is dissolved in a solvent. The solute is typically present in a smaller amount, while the solvent is present in a larger amount.
Q: What is Raoult's Law?
A:
Raoult's Law states that the vapor pressure of a solvent in a solution is directly proportional to the mole fraction of the solvent in that solution.
Q: What is meant by concentration of a solution?
A:
Concentration of a solution indicates how much solute is present in a given amount of solvent or solution. It can be expressed in various ways, such as molarity, molality, mass percentage, or parts per million.
Q: What is the difference between molarity and molality?
A:
Molarity (M) refers to the number of moles of solute per liter of solution, whereas molality (m) is the number of moles of solute per kilogram of solvent. The key difference is that molarity uses the total volume of the solution, while molality considers only the mass of the solvent, making molality independent of temperature.
Articles
Related Stories
|
Upcoming School Exams
Certifications By Top Providers
Explore Top Universities Across Globe
Questions related to CBSE Class 12th
On Question asked by student community
Have a question related to CBSE Class 12th ?
Hello,
Since you have passed 10th and 12th from Delhi and your residency is Delhi, but your domicile is UP, here’s how NEET counselling works:
1. Counselling Eligibility: For UP NEET counselling, your UP domicile makes you eligible, regardless of where your schooling was. You can participate in UP state counselling according to your NEET rank.
2. Delhi Counselling: For Delhi state quota, usually 10th/12th + residency matters. Since your school and residency are in Delhi, you might also be eligible for Delhi state quota, but it depends on specific state rules.
So, having a Delhi Aadhaar will not automatically reject you in UP counselling as long as you have a UP domicile certificate.
Hope you understand.
Hello,
You can access Free CBSE Mock tests from Careers360 app or website. You can get the mock test from this link : CBSE Class 12th Free Mock Tests
Hope it helps !
Yes, it is possible for a student who has done their 12th grade already to take upto 4 exams of their requirement. This is possible through the NIOS, NATIONAL INSTITUTE OF OPEN SCHOOLING. Get more info about the exam and the board through the following link.
For CBSE the PREVIOUS YEARS PAPERS can be accessed through the following link for the Concerned subjec by careers360.
Consequently Careers360 does also have a chapter wise scheme of PYQs, you can access the STUDY MATERIAL (PYQs.) from the following link -
https://school.careers360.com/boards/cbse/cbse-question-bank
Thankyou.
Hello,
Sorry, but JoSAA does not accept marks from two different boards for the same qualification during counselling. However, you can use your NIOS marks to meet the JEE Main/Advanced eligibility criteria if they are better than your CBSE marks. You can use your NIOS marks for the eligibility check, but when presenting your documents, you may be required to present both marksheets and the one with the higher marks for each subject will be considered.
I hope it will clear your query!!
Popular CBSE Class 12th Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
CBSE Class 12th Notifications
Never miss an CBSE Class 12th update
Get timely CBSE Class 12th updates directly to your inbox. Stay informed!