NCERT Solutions for Class 12 Chemistry Chapter 3 - Chemical Kinetics

Question 3.1(ii) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.

(ii) $H_{2}O_{2}(aq)+3I^{-}(aq)+2H^{+}\rightarrow 2H_{2}O(I)+I_{3}^{-}$ $Rate=k\left [ H_{2}O_{2}\right ]\left [ I^{-} \right ]$

Answer :

Given rate = $k[H_{2}O_{2}][I^{-}]$

Therefore, the order of the reaction is 2

Dimension of k = $rate/[H_{2}O_{2}][I^{-}]$

$\\=mol\ L^{-1}\ s^{-1}/(mol\ L^{-1})(mol\ L^{-1})\\$

$=L\ mol^{-1}\ s^{-1}$

Question 3.1(iii) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.

$CH_{3}CHO(g)\rightarrow CH_{4}(g)+CO(g)\: \: Rate=k\left [ CH_{3} CHO\right ]^{3/2}$

Answer :

Given $Rate = k[CH_{3}CHO]^{3/2}$

Therefore the order of the reaction is 3/2

and the dimension of k $=Rate/[CH_{3}CHO]^{3/2}$

$\\=molL^{-1}s^{-1}/(molL^{-1})^{3/2}\\$

$=molL^{-1}s^{-1}/mol^{3/2}L^{-3/2}\\$

$ =L^{1/2}\ mol^{-1/2}\ s^{-1}$

Question 3.1(iv) From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.

$C_{2}H_{5}Cl(g\rightarrow )C_{2}H_{4}(g)+HCL(g) \: Rate=k\left [ C_{2}H_{5}Cl \right ]$

Answer :

$rate = k[C_{2}H_{5}Cl]$

so the order of the reaction is 1

and the dimension of k = $rate/[C_{2}H_{5}Cl]$

$\\=molL^{-1}s^{-1}/mol L^{-1}\\ =s^{-1}$

Question 3.2 For the reaction:
$2A+B\rightarrow A_{2}B$
the rate = $k\left [ A \right ]\left [ B \right ]^{2}$ with $k=2.0\times 10^{-6}mol^{-2}L^{2}s^{-1}$ . Calculate the initial rate of the reaction when $\left [ A \right ]=0.1 mol L^{-1}\: \: ,\left [ B \right ]=0.2 mol L^{-1}$ . Calculate the rate of reaction after $\left [ A \right ]$ is reduced to $0.06molL ^{-1}$ .

Answer :

The initial rate of reaction =

$rate = k[A][B]^{2}$

Substitute the given values of [A], [B] and k,

rate = $2\times 10^{-6}\times 0.1\times (0.2)^{2}$

=8 $\times 10^{-9}mol^{-2}\ L^{2}\ s^{-1}$

When [A] is reduced from 0.1 mol/L to 0.06 mol/L $[A^{'}=0.06]$

So, conc. of A reacted = 0.1-0.06 = 0.04 mol/L

and conc. of B reacted = 1/2(0.04) = 0.02mol/L

conc. of B left = (0.2-0.02) = 0.18 mol/L $[B^{'}=0.18]$

Now, the rate of the reaction is (R) = $k[A^{'}][B^{'}]$

$=2\times 10^{-6}\times 0.06\times (0.18)^{2}$

= $3.89\times 10^{-6}$ $mol L^{-1}s^{-1}$

Question 3.3 The decomposition of $NH_{3}$ on the platinum surface is a zero-order reaction. What are the rates of production of $N_{2}$ and $H_{2}$ if $k=2.5\times 10^{-4}mol^{-1}L s^{-1}$ ?

Answer :

The decomposition of $NH_{3}$ on the platinum surface reaction

$2NH_{3}(s)\overset{Pt}{\rightarrow}N_{2}(g)+3H_{2}(g)$

therefore,

Rate = $-\frac{1}{2}\frac{d[NH_{3}]}{dt}=\frac{d[N_{2}]}{dt}=\frac{1}{3}\frac{d[H_{2}]}{dt}$

For zero order reaction rate = k

therefore, $-\frac{1}{2}\frac{d[NH_{3}]}{dt}=\frac{d[N_{2}]}{dt}=\frac{1}{3}\frac{d[H_{2}]}{dt}=k$

So $\frac{d[N_{2}]}{dt}= 2.5\times 10^{-4}mol\ L^{-1}\ s^{-1}$

and the rate of production of dihydrogen $(H_{2})$ = 3 $\times$ (2.5 $\times 10^{-4}$ ) $mol\ L^{-1}\ s^{-1}$

= 7.5 $\times 10^{-4}$ $mol\ L^{-1}\ s^{-1}$

Question 3.4 The decomposition of dimethyl ether leads to the formation of CH₄, H_2, and CO and the reaction rate is given by Rate $=k\left[\mathrm{CH}_3 \mathrm{OCH}_3\right]^{3 / 2}$The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e., Rate $=k\left[P_{\mathrm{CH}_3 \mathrm{OCH}_3}\right]^{3 / 2}$ If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?

Answer :

Given that

$rate = k(P_{CH_{3}OCH_{3}})^{3/2}$

So, the unit of rate is bar/min .( $bar\ min^{-1}$ )

And thus the unit of k = unit of rate $/(bar)^{3/2}$

$\\=bar\ min^{-1}/(bar)^{3/2}\\ =bar^{-1/2}min^{-1}$

Question 3.5: Mention the factors that affect the rate of a chemical reaction.

Answer :

The following factors affect the rate of reaction-

• The concentration of reactants
• temperature, and
• presence of a catalyst
• Surface area of reactants
• Pressure

Question 3.6(i) A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is doubled

Answer :

Let us assume the concentration of the reactant is x

So, rate of reaction, $R =k[x]^{2}$

Now, if the concentration of the reactant is doubled, then $x\rightarrow 2x$. So the rate of reaction would be $R = k[2x]^{2} = 4kx^{2}=4R$

Hence, we can say that the rate of reaction increased by 4 times.

Question 3.6(ii) A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is reduced to half?

Answer :

Let us assume the concentration of the reactant is x

So, rate of reaction, R = $k[x]^{2}$

Now, if the concentration of the reactant is doubled, then $x\rightarrow \frac{x}{2}$ . So the rate of reaction would be $R = k[\frac{x}{2}]^{2} = \frac{kx^{2}}{4}=\frac{R}{4}$

Hence, we can say that the rate of reaction is reduced to 1/4 times.

Question 3.7 What is the effect of temperature on the rate constant of a reaction? How can this effect of temperature on the rate constant be represented quantitatively?

Answer :

The rate constant is nearly double when there is a 10-degree rise in temperature in a chemical reaction.The

effect of temperature on the rate constant can be represented quantitatively by the Arrhenius equation.

$K =Ae^{-E_{a}/RT}$ where k is rate constant

A is the Arrhenius factor

R is the gas constant

T is temperature and

$E_{a}$ is the activation energy

Question 3.8 In pseudo-first-order hydrolysis of an ester in water, the following results were obtained:

(i) Calculate the average rate of reaction between the time intervals 30 to 60 seconds.

Answer :

The average rate of reaction between 30 s and 60 s is expressed as

$R = \frac{d[ester]}{dt}$

$\\=(0.31-0.17)/60-30\\ $

$=0.14/30=4.67\times 10^{-3} mol\ L^{-}\ s^{-}$

Question 3.9(i) A reaction is first order in A and second order in B.

(i)Write the differential rate equation.

Answer :

The reaction is first order in A and second order in B. it means the power of A is one and the power of B is 2

The differential rate equation will be

$-\frac{d[R]}{dt}=k[A][B]^{2}$

Question 3.9(ii) A reaction is first order in A and second order in B.

(ii) How is the rate affected by increasing the concentration of B three times?

Answer :

If the concentration of [B] is increased by 3 times, then

$-\frac{d[R]}{dt}=k[A][3B]^{2}$

$=9k[A][B]^{2}$

Therefore, the rate of reaction will increase 9 times.

Question 3.9(iii) A reaction is first order in A and second order in B.

(iii) How is the rate affected when the concentrations of both A and B are doubled?

Answer :

If the concentration of [A] and[B] is increased by 2 times, then

$-\frac{d[R]}{dt}=k[2A][2B]^{2}$

$=8k[A][B]^{2}$

Therefore, the rate of reaction will increase 8 times.

Question 3.10 In a reaction between A and B, the initial rate of reaction (r0) was measured for different initial concentrations of A and B as given below:

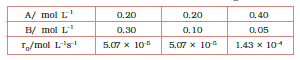
What is the order of the reaction with respect to A and B?

Answer :

we know that
rate law ( $r_{0}$ ) = $k[A]^{x}[B]^{y}$
As per data

$\\5.07\times 10^{-5} =k[0.2]^{x}[0.3]^{y}\\ 5.07\times 10^{-5}$

$=k[0.2]^{x}[0.1]^{y}\\ 1.43\times 10^{-4}$

$=k[0.4]^{x}[0.05]^{y}$

These are equations 1, 2 and 3, respectively

Now, divide eq.1 by equation 2, we get
$1= (0.3/0.1)^{y}$
from here, we calculate that y = 0

Again, dividing Eq. 2 by Eq. 3, we get
Since y =0, also substitute the value of y
So,
= $(\frac{1.43}{0.507})= (\frac{0.4}{0.2})^{x}$
= $2.821=2^{x}$

Taking the log of both sides, we get,

$x = \frac{\log2.821}{\log2}$
= 1.496
= approx 1.5
Hence the order of reaction w.r.t A is 1.5 and w.r.t B is 0(zero)

Question 3.11 The following results have been obtained during the kinetic studies of the reaction:
2A + B $\rightarrow$ C + D

Determine the rate law and the rate constant for the reaction .

Answer :

Let assume the rate of reaction wrt A is $x$ and wrt B is $y$ . So, the rate of reaction is expressed as-
Rate = $k[A]^{x}[B]^{y}$

According to given data,
$\\6\times 10^{-3}=k[0.1]^{x}[0.1]^{y}\\ 7.2\times 10^{-2}$

$=k[0.3]^{x}[0.2]^{y}\\ 2.88\times 10^{-2$}$

$=k[0.3]^{x}[0.4]^{y}\\ 2.4\times 10^{-2}$

$=k[0.4]^{x}[0.1]^{y}$

These are equations 1, 2, 3 and 4, respectively

Now, divide the equation(iv) by (i) we get,
$4 = (0.4/0.1)^{x}$
from here, we calculate that $x =1$

Again, divide equation (iii) by (ii)
$4 =(0.4/0.2)^{y}$
from here, we can calculate that the value of y is 2

Thus, the rate law is now, $Rate = k[A][B]^{2}$
So, $k = rate/[A][B]^{2}$
$\\= 6\times 10^{-3}/(0.1)\times (0.1)^{2}\\$

$ =6\ L^{2}\ mol^{-2}\ min^{-1}$

Hence the rate constant of the reaction is $=6\ L^{2}\ mol^{-2}\ min^{-1}$

Question 3.12 The reaction between A and B is first order with respect to A and zero order
With respect to B. Fill in the blanks in the following table:

Answer :

The given reaction is first order wrt A and zero order in wrt B. So, the rate of reaction can be expressed as;
$Rate = k[A][B]^{0}$
Rate = k[A]

from exp 1,
$2\times 10^{-2}=k(0.1)$
k = 0.2 per min.

from experiment 2nd,
$4\times 10^{-2}=0.2[A] \\$
[A] = $0.2\ mol/L$

from experiment 3rd,
$rate =(0.2\ min^{-1})\times (0.4\ mol/L)$
$= 0.08\ mol\ L^{-1}\ min^{-1}$

from the experiment 4th,

$2\times 10^{-2}=0.2*[A]$
from here [A] = 0.1 mol/L

Question 3.13 (1) Calculate the half-life of a first-order reaction from their rate constants given below:
$200 s^{-1}$

Answer :

We know that,
half-life ( $t_{1/2}$ ) for first-order reaction = $0.693/k$
= $0.693/200$
$\approx 3.4\times 10^{-3}s$

Question 3.13 (2) Calculate the half-life of a first-order reaction from their rate constants given below:
$2\: \: min ^{-1}$

Answer :

The half-life for the first-order reaction is expressed as ;

$t_{1/2}=0.693/k$
= 0.693/2
= 0.35 min (approx)

Question 3.13 (3) Calculate the half-life of a first-order reaction from their rate constants given below:
4 $years ^{-1}$

Answer :

The half-life for the first-order reaction is $t_{1/2}= 0.693/k$
= 0.693/4
= 0.173 year (approximately)

Question 3.14 The half-life for radioactive decay of $^{14} C$ is 5730 years. An archaeological artefact containing wood had only 80% of the 14C found in a living tree. Estimate the age of the sample.

Answer :

Given,
half-life of radioactive decay = 5730 years
So, $t_{1/2}= 0.693/k$
$k = 0.693/5730$ per year

We know that, for a first-order reaction,
$t = \frac{2.303}{k} \log\frac{[R_{0}]}{[R]}$
$t = \frac{2.303}{.693/5730} \log\frac{100}{80}$
= 1845 years (approximately)

Thus, the age of the sample is 1845 years

Question 3.15 (1) The experimental data for the decomposition of

$2 N_2 O_5 \rightarrow 4 NO_2 + O_2$
In the gas phase at 318K are given below:

Plot $[N_2O_5]$ against t.

Answer :

On increasing time, the concentration of $N_{2}O_{5}$ gradually decreasing exponentially.

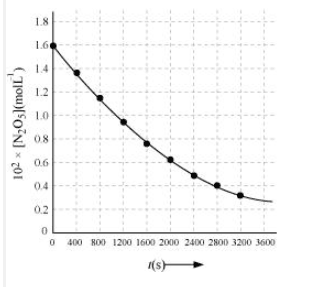
Question 3.15 (2) The experimental data for decomposition of $2 N_2O_5 \rightarrow 4 NO_2 + O_2$ in gas phase at 318K are given below:

Find the half-life period for the reaction.

Answer :

The half-life of the reaction is-
The time corresponding to the $1.63 \times 10^{2}/2$ mol/ L = 81.5 mol /L is the half-life of the reaction. From the graph, the answer should be in the range of 1400 s to 1500 s.

Question 3.15 (3) The experimental data for decomposition of $N_2O_5 [2N_2O_5 \rightarrow 4NO_2 + O_2]$ in the gas phase at 318K are given below:

Draw a graph between $\log [ N_2 O_5 ]$ and t.

Answer :

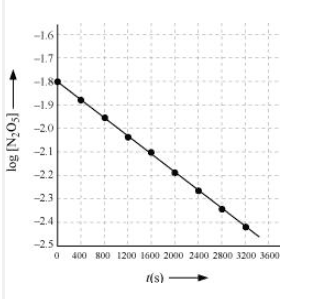
Question 3.15 (4) The experimental data for decomposition of $N_2O_5 [2N_2O_5 \rightarrow 4NO_2 + O_2]$ in the gas phase at 318K are given below:

What is the rate law?

Answer :

Here, the reaction is a first-order reaction because its log graph is linear.
Thus rate law can be expessed as $Rate = k[N_{2}O_{5}]$

Question 3.15 (5) The experimental data for decomposition of $N_2O_5 [2N_2O_5 \rightarrow 4NO_2 + O_2]$ in the gas phase at 318K are given below:

Calculate the rate constant.

Answer :

From the log graph,

the slope of the graph is = $\frac{-2.46-1.79}{3200}$
= -k/2.303 ..(from log equation)

On comparing both the equation, we get,

$-k/2.303 = -0.67/3200$
$k= 3200\times (0.67/3200)$
$k= 4.82 \times 10^{-4}\ s^{-1}$

Question 3.15 (6) The experimental data for decomposition of $N_2O_5 [2N_2O_5 \rightarrow 4NO_2 + O_2]$ in the gas phase at 318K are given below:

Calculate the half-life period from k and compare it with (ii).

Answer :

The half life produce = $0.693/k$
= $=0.693/4.82 \times 10^{-4}$
$1.438\times 10^{3} s$

Question 3.15(7) The rate constant for a first-order reaction is $60 s^{-1}$. How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?

Answer :

We know that,
for a first-order reaction,
$t=\frac{2.303}{k}\log\frac{[R]_{0}}{[R]}$
$\\=\frac{2.303}{60}\log\frac{1}{1/16}\\ $

$=\frac{2.303}{60} \log2^{4}$
$=4.6 \times 10^{-2} s$ (nearly)

Hence the time required is $=4.6 \times 10^{-2} s$

Question 3.17 During a nuclear explosion, one of the products is $^{90} Sr$ with a half-life of 28.1 years. If $1 \mu g$ of $^{90}Sr$ was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically?

Answer :

Given,
half life = 21.8 years
$\therefore\ k=0.693/t_{1/2}$
= 0.693/21.8

and, $t = \frac{2.303}{k}\log\frac{[R]_{0}}{[R]}$

by putting the value we get,

$10= \frac{2.303}{0.693/21.8}\log\frac{1}{[R]}$
$\log[R] = -\frac{10\times 0.693}{2.303\times 21.8}$
Taking antilog on both sides,
[R] = antilog(-0.1071)
= 0.781 $\mu g$

Thus, 0.781 $\mu g$ of ${Sr}^{90}$ will remain after 10 years.

Again,

$\begin{aligned} & t=\frac{2.303}{k} \log \frac{[\mathrm{R}]_0}{[\mathrm{R}]} \\ & \Rightarrow 60=\frac{2.303}{\frac{0.693}{28.1}} \log \frac{1}{[\mathrm{R}]} \\ & \Rightarrow \log [\mathrm{R}]=-\frac{60 \times 0.693}{2.303 \times 28.1} \\ & \begin{aligned} \Rightarrow[\mathrm{R}] & =\operatorname{antilog}(-0.6425) \\ & =\operatorname{antilog}(\overline{1} .3575) \\ & =0.2278 \mu \mathrm{~g}\end{aligned}\end{aligned}$
Thus 0.2278 $\mu g$ of ${Sr}^{90}$ will remain after 60 years.

Question 3.18 For a first-order reaction, show that the time required for 99% completion is twice the time required for the completion of 90% of the reaction.

Answer :

Case 1-

for 99% complition,
$t^{1} = \frac{2.303}{k}\log\frac{100}{100-99}$
$= \frac{2.303}{k}\log100$
$=2\times (\frac{2.303}{k})$

Case- II
for 90% completion,

$t^{2}=\frac{2.303}{k}\log\frac{100}{100-90}$
$=\frac{2.303}{k}\log10$
$=(\frac{t^{1}}{2})$

$t^{1}=2t^{2}$
Hence proved.

Question 3.19 A first-order reaction takes 40 min for 30% decomposition. Calculate $t_{1/2}$

Answer :

For the first-order reaction,

$t =\frac{2.303}{k}\log \frac{[R]_{0}}{[R]}$
$k =\frac{2.303}{40}\log \frac{100}{100-30}$ (30% already decomposed and remaining is 70%)

$=8.918\times 10^{-3} min^{-1}$

therefore half life = 0.693/k
= $0.693/8.918\times 10^{-3}$
= 77.7 (approx)

Question 3.20 For the decomposition of azoisopropane to hexane and nitrogen at 543K, the following data are obtained.

Calculate the rate constant.

Answer :

This decomposition is first-order, and in gas-phase kinetics, pressure can be used in place of concentration if temperature and volume are constant.

For a first-order reaction, the integrated rate law is:

$
k=\frac{1}{t} \ln \left(\frac{P_{\infty}-P_0}{P_{\infty}-P_t}\right)
$
Where:
- $P_0=35.0 \mathrm{mmHg}$ (initial pressure)
- $P_t$ is pressure at time $t$
- $P_{\infty}=2 P_0=70.0 \mathrm{mmHg}$ (since $1 \mathrm{~mol} \rightarrow 2 \mathrm{~mol}$ gases)

Step 2: Calculate rate constant using data at $t=360 \mathrm{~s}$

$
\begin{gathered}
k=\frac{1}{360} \ln \left(\frac{70-35}{70-54}\right)=\frac{1}{360} \ln \left(\frac{35}{16}\right)=\frac{1}{360} \ln (2.1875) \\
\ln (2.1875) \approx 0.7827 \\
k=\frac{0.7827}{360} \approx 2.174 \times 10^{-3} \mathrm{~s}^{-1}
\end{gathered}
$

$
k \approx 2.17 \times 10^{-3} \mathrm{~s}^{-1}
$

Question 3.21 The following data were obtained during the first order thermal decomposition of $SO_2 Cl_2$ at a constant volume.
$( SO_2Cl_2 g) \rightarrow SO_2 (g) + Cl_2 (g)$

Calculate the rate of the reaction when the total pressure is 0.65 atm.

Answer :

The thermal decomposition of $SO_{2}Cl_{2}$ is shown here;

$
\mathrm{SO}_2 \mathrm{Cl}_2 \rightarrow \mathrm{SO}_2+\mathrm{Cl}_2
$

Initial pressure $\quad p_0 \quad 0 \quad 0$
Pressure at time $t \quad p_0-p \quad p \quad p$
Let initial pressure, $P_0 \propto R_0$
Pressure at time t $p_t=p_0-p+p+p=p_0+p$
Pressure of reactants at time t $ p_0-p=2 p_0-p_t \propto R$

After t time, the total pressure $p_{t}$ = $p_{0}-p+(p+p) = p_{0}+p$

So, $p = p_{t}-p_{0}$

thus, $p_{0}-p = 2p_{0}-p_{t}$

for a first-order reaction,

$k= \frac{2.303}{t}\log\frac{p_{0}}{p_{0}-p}$
$= \frac{2.303}{360}\log\frac{p_{0}}{2p_{0}-p_{t}}$
now putting the values of pressures, when t = 100s
$k = \frac{2.303}{100}\log\frac{0.5}{2*0.5-0.6}$
$= 2.231 \times 10^{-3}\ s^{-1}$

when $p_{t} = 0.65\ atm$

$p = p_{t}-p_{0}$
= 0.65 - 0.5
= 0.15 atm

So, $p(_{SO_{2}Cl_{2}}) = p_{0}-p$
= 0.5 - 0.15
= 0.35 atm

Thus, rate of reaction, when the total pressure is 0.65 atm
rate = k( $p(_{SO_{2}Cl_{2}})$ )
= $2.31\times 10^{-3}\times 0.35$
= 7.8 $\times 10^{-4}\ atm\ s^{-1}$

Question 3.22 The rate constant for the decomposition of $N_{2}O_{5}$ at various temperaturesis given below:

Draw a graph between ln k and 1/T and calculate the values of A and
$E_a$ . Predict the rate constant at 30° and 50°C.

Answer :

From the above data,

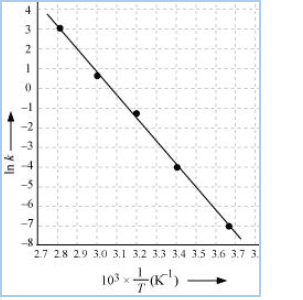
Slope of line = $\frac{y2-y2}{x2-x1} = -12.30\ K$

According to Arrhenius equations,

Slope = $-E_{a}/R$
$E_{a}=$ 12.30 $\times$ 8.314
= 102.27 $KJ mol^{-1}$

Again,

$
\begin{aligned}
& \ln k=\ln A-\frac{E_a}{\mathrm{R} T} \\
& \ln A=\ln k+\frac{E_a}{\mathrm{R} T}
\end{aligned}
$

When $T=273 \mathrm{~K}$,
$\ln k=-7.147$

When $T=273 \mathrm{~K}$,

$\ln k=-7.147$

Then, $\ln A=-7.147+\frac{102.27 \times 10^3}{8.314 \times 273}$

$=37.911$

Therefore, $A=2.91 \times 10^6$
When T = 30 +273 = 303 K and 1/T =0.0033K
$\ln k= -2.8$

$\therefore$ k = $6.08\times 10^{-2}\ s^{-1}$

When T = 50 + 273 = 323 K and 1/T = 3.1 $\times 10^{-3}$ K
$\ln k = -0.5$
$\therefore$ k = 0.607 per sec

Question 3.23 The rate constant for the decomposition of hydrocarbons is $2.418 \times 10 ^{-5} s ^{-1}$ at 546 K. If the energy of activation is 179.9 kJ/mol, what will be the value of the pre-exponential factor?

Answer :

Given that,
k = $2.418 \times 10 ^{-5} s ^{-1}$
$E_{a}$ = 179.9 KJ/mol
T(temp) = 546K

According to Arrhenius equation,

$k=Ae^{-E_{a}/RT}$
taking log on both sides,
$\log k = \log A - \frac{E_{a}}{2.303 RT}$

$\log A =\log k + \frac{E_{a}}{2.303 RT}$

$=\log (2.418\times 10^{-5}) + \frac{179.9\times 10^{3}}{2.303 \times 8.314 \times 546}$

= (0.3835 - 5) + 17.2082
= 12.5917
Thus A = antilog (12.5917)
A = 3.9 $\times 10^{12}$ per sec (approx)

Question 3.24 Consider a certain reaction A $\rightarrow$ Products with $k = 2.0 \times 10 ^{-2 } s ^{-1}$ . Calculate the concentration of A remaining after 100 s if the initial concentration of A is 1.0 mol $L^{-1}$

Answer :

Given that,
k = $=2\times 10^{-2}$
t = 100 s
$[A]_0= 1\ mol\ L^{-1}$
Here, the unit of k is in per sec, it means it is a first-order reaction.
therefore,
$k = \frac{2.303}{t}\log\frac{[A]_o}{[A]}$
$\\2\times 10^{-2} = \frac{2.303}{100}\log\frac{1}{[A]}\\ 2\times 10^{-2} $

$= -\frac{2.303}{100}\log[A]\\ \log[A]=-\frac{2}{2.303}\\$
$\\A = anti\log\frac{-2}{2.303}\\ A= 0.135 mol\ L^{-1}$

Hence, the concentration of the rest test sample is 0.135 mol/L

Question 3.25 Sucrose decomposes in an acid solution into glucose and fructose according to the first-order rate law, with $t _{1/2 } = 3.00$ hours. What fraction of the sample of sucrose remains after 8 hours?

Answer :

For first-order reaction,

$k = \frac{2.303}{t}\log\frac{[R]_{0}}{[R]}$

given that half life = 3 hrs ( $t_{1/2}$ )

Therefore k = 0.693/half-life
= 0.231 per hour

Now,

$\\0.231 = \frac{2.303}{8}\log\frac{[R]_{0}}{[R]}\\ \log\frac{[R]_{0}}{[R]} $

$= 0.231\times \frac{8}{2.203}$
= antilog (0.8024)
= 6.3445

$[R]_{0}/[R] = 6.3445$

$[R]/[R]_{0} = 0.157$ (approx)

Therefore, the fraction of the sample of sucrose remains after 8 hrs is 0.157

Question 3.26 The decomposition of hydrocarbon follows the equation k=(4.51011s^-1)e^-28000K/T . Calculate $E_{a}$

Answer :

The Arrhenius equation is given by
$k=Ae^{-E_{a}/RT}$ .................................(i)
given equation,

A= 4.51011 per sec.............(ii)

by comparing equation (i) & (ii) we get,

A= 4.51011 per sec
$E_{a}/RT =28000/T$
Activation energy = 28000 $\times$ (R = 8.314)
= 232.792 KJ/mol

Question 3.27 The rate constant for the first order decomposition of $H_2O_2$ is given by the following equation:
$\log k = 14.34 - 1.25 \times 10 ^ 4K/T$ .

Calculate $E_a$ for this reaction and at what temperature will its half-period be 256 minutes?

Answer :

The Arrhenius equation is given by
$k=Ae^{-E_{a}/RT}$

Taking the log on both sides,

$\log k = \log A -\frac{E_{a}}{2.303RT}$ ....................(i)
given equation,

$\log k = 14.34 - 1.25 \times 10 ^ 4K/T$ .....................(ii)

On comparing both equation, we get,

$E_{a}/2.303R=1.25 \times 10^{4}$

activation energy
$\\=1.25 \times 10^{4} \times 2.303 \times 8.314\\ $

$=239.34\ KJ/mol$

half life ( $t_{1/2}$ ) = 256 min

k = 0.693/256
$k = 4.51\times 10^{-5} s^{-1}$

With the help of equation (ii),

$\log4.51\times 10^{-5} s^{-1} = 14.34-\frac{1.25\times 10^{4}}{T}$

$\frac{1.25\times 10^{4}}{T} = 18.686$
T = $\frac{1.25\times 10^{4}}{18.686}$

= 669 (approx)

Question 3.28 The decomposition of A into product has value of k as $4.5 \times 10 ^3 s ^{-1}$ at 10°Cand energy of activation 60 kJ $mol^{-1}$. At what temperature would k be $1.5 \times 10 ^4 s ^{-1}$ ?

Answer :

The decomposition of A into a product has a value of k as $4.5 \times 10 ^3 s ^{-1}$ at 10°C and energy of activation 60 kJ mol–1.

K₁ = $4.5 \times 10 ^3 s ^{-1}$
K₂ = $1.5 \times 10 ^4 s ^{-1}$

$E_a$ = 60 kJ mol–1

K₂ = $1.5 \times 10 ^4 s ^{-1}$

$log\frac{K_2}{K_1}=\frac{E_a(T_2-T_1)}{2.303RT_1T_2}$

$log(\frac{1.5\times 10^{4}}{4.5\times 10^{3}})=\frac{60(T_2-283)}{2.303\times R\times 283\times T_2}$

$log(\frac{150}{45})=\frac{60(T_2-283)}{5418.61\times T_2}$

$log150-log45=\frac{60T_2-16980}{5418.61\times T_2}$

$2.176-1.653=\frac{60T_2-16980}{5418.61\times T_2}$

$0.5229=\frac{60T_2-16980}{5418.61\times T_2}$

$T_2=\frac{16980}{2733.4}$

$T_2=6.1K$

Question 3.29 The time required for 10% completion of a first order reaction at 298K is equal to that required for its 25% completion at 308K. If the value of A is $4 \times 10 ^{10} s ^{-1}$ . Calculate k at 318K and E_a.

Answer :

We know that,

for a first order reaction-

$t = \frac{2.303}{k}\log\frac{a}{a-x}$

Case 1
At temp. = 298 K
$t = \frac{2.303}{k}\log\frac{100}{90}$
= 0.1054/k

Case 2
At temp = 308 K

$t' = \frac{2.303}{k}\log\frac{100}{75}$
= 2.2877/k'
As per the question
$t' = t$
K'/K = 2.7296

From the Arrhenius equation,

$\begin{aligned} & \log \frac{k^{\prime}}{k}=\frac{E_a}{2.303 \mathrm{R}}\left(\frac{T^{\prime}-T}{T T^{\prime}}\right) \\ & \log (2.7296)=\frac{E_a}{2.303 \times 8.314}\left(\frac{308-298}{298 \times 308}\right) \\ & E_a=\frac{2.303 \times 8.314 \times 298 \times 308 \times \log (2.7296)}{308-298}\end{aligned}$
= 76640.096 J /mol
=76.64 KJ/mol

k at 318 K
we have , T =318K
A= $4 \times 10^{10}$

Now $\log k = \log A- \frac{E_{a}}{2.303RT}$
After putting the value of the given variable, we get

$\log k = -1.9855$
On taking antilog we get,

k = antilog(-1.9855)

= 1.034 $\times 10^{-2}\ s^{-1}$

Question 3.30 The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction, assuming that it does not change with temperature.

Answer :

From the Arrhenius equation,

$\log\frac{k_{2}}{k_{1}}=\frac{E_{a}}{2.303R}(\frac{T_{2}-T_{1}}{T_{1}T_{2}})$ ...................................(i)
it is given that $k_{2}=4k_{1}$
T1= 293 K

T2 = 313 K
Putting all these values in equation (i) we get,

$\log 4 =\frac{E_{a}}{2.303 \times 8.314}(\frac{313-293}{313 \times 293})$

$\begin{aligned} & \Rightarrow 0.6021=\frac{20 \times E_a}{2.303 \times 8.314 \times 293 \times 313} \\ & \Rightarrow E_a=\frac{0.6021 \times 2.303 \times 8.314 \times 293 \times 313}{20}\end{aligned}$

Activation Energy = 52.86 KJ/mol
This is the required activation energy