NCERT Class 12 Physics Chapter 2 Notes - Electrostatic Potential and Capacitance

NCERT Class 12 Physics Chapter 2 Notes: Download PDF

NCERT Class 12 Physics Chapter 2 Notes Electric Potential and Capacitance are useful as a quick learning and revision resource. All the major concepts, formulas, and derivations have been addressed in these notes in a simplified form, through which students are able to learn tough topics quickly and prepare successfully to pass CBSE board exams and even JEE/NEET. They are a great last minute tool and a concept clarifier.

Download PDF

NCERT Class 12 Physics Chapter 2 Notes

The NCERT Class 12 Physics Chapter 2 Notes Electric Potential and Capacitance are crucial for revision and last-minute study. Using these notes, students can view all the topics and prepare for their exams.

Electric Potential:

The electrostatic potential in a region of the electric field is equal to the amount of work done in bringing a unit-positive test charge from infinity to that point against the electrostatic force.

V=Wqo

Where,

W - work done and qo - unit charge

• Electric potential is a scalar quantity and the SI unit is Volt (V).
• CGS unit is stat-volt.
• Dimension - ML2T−3A−1.
• 1 volt =1300 stat volt.

Potential due to a system of point charges:

V=∑i=1nKQiri

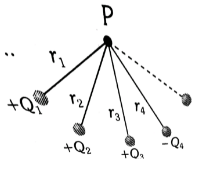
Potential difference:

The potential difference between two points A and B in an electric field is equal to the amount of work done (by an external agent) in moving a unit positive charge from point A to point B.

VA=Electric potential at point A

VB=Electric potential at point B

VB−VA=Wq

rB→ the distance of charge at B
rA→ distance of charge at A
ΔV= The Electric potential difference in bringing charge q from point A to point B in the Electric field produced by Q.

ΔV=VB−VA=WA→BqΔV=KQ[1rB−1rA]

Where,

W is the amount of work done and q is the unit positive charge.

Electric potential due to a point charge:

V=KqrK=14πϵ0

The relation between the electric field and the potential

E→=−dVdr

Where E is the Electric field
And V is the Electric potential
And r is the position vector
A negative sign indicates that in the direction of intensity, the potential decreases.
If r→=xi→+yj→+zk→

Then Ex=δVdx,Ey=δVdy,Ez=δVdz
where

Ex=−∂Vdx (partial derivative of V w.r.t. x) Ey=−∂Vdy (partial derivative of V w.r.t. y) Ez=−∂Vdz (partial derivative of V w.r.t. z)

Potential Due to an Electric Dipole

A. On the Axial Line:

As shown in the above figure, we want to find out the Electric Potential due to an Electric Dipole at a Point M, which is on the axial line and at a distance r from the centre of a dipole.

Where V1 and V2 is the Electric Potential at M due to −q and +q charges respectively.

V1=kq(r+a)V2=kq(r−a)Vnet =V2−V1Vnet =V1+V2=−kq(r+a)+kq(r−a)=kq{1r−a−1r+a}=kq{(r+a)−(r−a)(r−a)(r+a)}

So Vnet =2kqar2−a2
Using P=q(2a)
So Vnet =kPr2−a2
- if r≫a
then Vnet=KPr2=P4πϵ0r2

B. On the Equitorial line:

As shown in the above figure We want to find out Electric potential due to an Electric Dipole at a Point M which is on the Equitorial line and at a distance r from the centre of a dipole.

Where V1 and V2 is the Electric Field Intensity at M due to −q and +q charges respectively.

V1=−14πϵ0∗qr2+a2V2=14πϵ0∗qr2+a2Vnet =V2−V1=0

C. At any general point:

As shown in the above figure, we want to find out the Electric potential due to an Electric Dipole at a Point M, which is at a distance r from the centre of a dipole and making an angle with the axial line.

From the figure, M is at the axial line of the dipole, having a dipole moment as Pcos⁡θ, and M is at the equatorial line of the dipole, having a dipole moment as Psin⁡θ.
So Psin⁡θ has no contribution to the electric potential at point M.
if r>>a
then
Va=14πε0×2Pcos⁡θr2 and V⊥=0
SoVnet =Va=KPcos⁡θr2

Electric Potential Energy:

Consider a system with two charges, q₁ and q₂ fixed at points A and B, respectively, and separated by AB =r₂. If q₂ is moved from B to a new point C along AB and AC =r₂, and the charge is displaced from r to r + dr, then the work done (dW) is as follows:

dW=F.dr =Kq1q2r2⋅dr

• Total work done

W=∫r1r2Kq1q2r2⋅dr=q1q24πϵ0[1r1−1r2]

• Change in potential energy

U(r2)−U(r1)=−W=q1q24πϵ0[1r2−1r1]

• When the system of two charges has infinite separation, thenthe potential energy

U(∞)=0

• The potential energy when separation is r is

U(r)0=U(r)−U(∞)=q1q24πϵ0r

Equipotential Surface

An equipotential surface is a surface where the electric potential remains constant at every point. This means that no work is required to move a charge along this surface because the potential difference between any two points is zero.

• The electric field is always perpendicular to an equipotential surface.
• No work is done when moving a charge along an equipotential surface.
• In a uniform electric field, equipotential surfaces are parallel planes.
• For a point charge, equipotential surfaces are concentric spheres centred around the charge.

Work done in the rotation of a dipole and the equilibrium of a dipole:

W=pE(cos⁡Θ1−cos⁡Θ2)W=pE(cos⁡Θ1−cos⁡Θ2) if θ1=90 and θ2=θW=−pEcos⁡θ=−p→.E→

This work done is stored as potential energy.

Condition for the stable equilibrium of a dipole:

1. Angle (θ): The system is stable when the angle between the dipole moment (p) and the electric field (E) is 0° (aligned).
2. Torque: In this position, the net torque acting on the dipole is zero. Any slight deviation from this position causes a restoring torque, bringing the dipole back into alignment with the field.
3. Potential Energy: When the dipole is aligned with the electric field, its potential energy is at its lowest.

Condition for the unstable equilibrium of a dipole:

1. Angle (θ): The system is in unstable equilibrium when the angle between p and E is 180° (anti-aligned).
2. Torque: In this position, the net torque acting on the dipole is zero. Any small displacement from this position, however, produces a torque that increases the angle between p and E, pushing the dipole out of alignment.
3. Potential Energy: The dipole's potential energy is greatest when it is anti-aligned with the electric field.

Electrostatics of Conductors

• At electrostatic equilibrium, the electric field inside a charged conductor is zero.
• The electric field at every point on the surface of a charged conductor is normal (perpendicular) to the surface.
• In a static situation, the excess charge on a charged conductor exists only on its surface.
• There is no electric field inside the cavity of a conductor, providing electrostatic shielding.
• At electrostatic equilibrium, the electrostatic potential remains constant throughout the conductor.

Dielectrics and Polarisation

• Dielectrics are non-conducting materials, and they do not have free charge carriers that can move easily within the material.

Non-Polar Molecules:

The centres of negative and positive charges coincide in a non-polar molecule. The non-polar molecule lacks a permanent dipole moment.

Example: O₂, H₂

Polar Molecule:

Polar molecules have negative and positive charge centres that are separated and have a permanent dipole moment.

Example: H₂O, HCl

NOTE: Both polar and non-polar dielectrics acquire a net dipole moment in the presence of an external electric field.

Polarization:

It is the dipole moment per unit volume

P=χeE

χe is the electric susceptibility of the dielectric medium

• Polarised dielectrics are similar to two charge surfaces with an induced charge density of opposite polarity.

Capacitor

A capacitor is a system of two conductors, which are separated by an insulator. A capacitor is used to store a large amount of charge.

The charge stored in a capacitor:

Q=CV

where C is capacitance and V is voltage

Capacitance (C):

The capacitance of a capacitor

C=Q/V

Dielectric Strength:

Dielectric strength is the maximum amount of electric field that a dielectric medium can withstand.

Parallel Plate Capacitor:

Two conducting plates of area A are separated by a distance d. If the dielectric medium between the capacitor plate is vacuum or air, then

C=ϵ0Ad

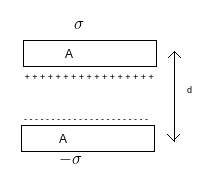
• When a dielectric of dielectric constant k is inserted between the above capacitor, the new capacitance

C′=kϵ0AdC′=kCC

Combination of capacitors:

Series Combination :

In series: 1Ceq=1C1+1C2+1C3+.
Note: In a series combination equivalent capacitance is always less than the smallest capacitor of the combination.

Parallel Combination :

Equivalent capacitance of parallel combination Ceq=C1+C2+C3

Note: Equivalent capacitance is always greater than the largest capacitor of cthe ombination.

• For n capacitors connected in parallel, the net value of capacitance is

C=C1+C2+C3+………Cn

• For n capacitors connected in series, the net value of capacitance is

1C=1C1+1C2+1C3+……………1Cn

Energy Stored in a Capacitor:

The energy U stored in a capacitor of capacitance C, charge Q and voltage V is

U=12CV2

The electric energy density

In a region with an electric field, the electric energy density,

Energy per unit volume =12ϵ0E2

Electric Potential and Capacitance: Previous Year Question and Answer

Q1: A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge

A. remains a constant because the electric field is uniform

B. increases because the charge moves along the electric field

C. decreases because the charge moves along the electric field

D. decreases because the charge moves opposite to the electric field

Answer:

A positively charged particle in a uniform electric field experiences a force in the direction of the electric field.
When the charge moves along the direction of the field, it moves to a region of lower electric potential.
As it moves, the electric potential energy decreases because the work done by the field on the charge reduces the potential energy and converts it into kinetic energy.

Hence, the correct answer is option (C).

Q2: Two point charges 4μC and +1μC are separated by a distance of 2 m in air. Find the point on the line joining charges at which the net electric field of the system is zero.

Answer:

Let the electric field be zero at p at a distance x from a 1μc charge, then
k×4μc(2−x)2=k×1μcx2
22−x=1x
2x=2−x
x=23m
∴2−x=2−23=43m

Q3: Draw the equipotential surfaces corresponding to a uniform electric field in the z-direction.

Answer:

We know that the electric field strength is proportional to the distance between the surfaces, so the surface will be evenly spaced.

The electric field is always perpendicular to the equipotential surface.

Hence, the equipotential surfaces are going to be infinite plane sheets in the z-direction parallel to the x-y plane.

Importance of NCERT Class 12 Physics Chapter 2 Notes Electric Potential and Capacitance

Deepens Basic Understanding of Electrostatics

• Introduces important concepts like electric potential, potential energy, and their relationship to the electric field by focusing on Coulomb's law and electric fields.
• These concepts are essential to understand energy-based solutions for electrostatic problems.

Bridges Theory with Real-Life Applications

• Explains how capacitors are used in devices like filters, cellphones, and camera flashes to effectively store and release energy.
• Highlights attention to the usefulness of capacitors in power and electronics systems.

Clarifies Fundamental Definitions

• The work required per unit charge to move it from infinity to a point without acceleration is known as electrostatic potential, or V.
• Introduces equipotential surfaces, emphasizing their practical and visual importance in visualizing electric fields.

Strengthens Understanding of Energy Storage

• Demonstrates how capacitors store energy in an electric field with formula
• This knowledge is essential for electronics-related topics as well as general and competitive exam problem-solving.

Improves the Ability to Solve Numerical Problems

• Important formulas, derivations, and problem-solving strategies for concepts like potential difference, capacitor energy, and dielectric media behavior are included in the notes.

Perfect for Effective Exam Revision

• Students can review the chapter more quickly and confidently before tests when they have organized notes with labeled diagrams, essential formulas, and clear definitions.

NCERT Class 12 Notes Chapterwise

NCERT Class 12 Physics Notes are a handy resource for students preparing for board exams and competitive exams like JEE and NEET. These chapterwise notes simplify complex concepts with clear explanations, key formulas, and diagrams to make revision quick and effective. With easy-to-understand content, students can strengthen their fundamentals and improve problem-solving skills.

Subject Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 12 Solutions

• NCERT Exemplar Class 12 Maths

• NCERT Exemplar Class 12 Physics

• NCERT Exemplar Class 12 Chemistry

• NCERT Exemplar Class 12 Biology

Subject Wise NCERT Solutions

• NCERT Solutions for Class 12 Mathematics

• NCERT Solutions for Class 12 Chemistry

• NCERT Solutions for Class 12 Physics

• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus