• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Miscellaneous Exercise Chapter 6 Class 12 - Application of Derivatives

NCERT Solutions for Miscellaneous Exercise Chapter 6 Class 12 - Application of Derivatives

Edited By Ramraj Saini | Updated on Dec 04, 2023 01:17 PM IST | #CBSE Class 12th

NCERT Solutions For Class 12 Chapter 6 Miscellaneous Exercise

NCERT Solutions for miscellaneous exercise chapter 6 class 12 Application of Derivatives are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Students can get the NCERT solutions for Class 12 Maths chapter 6 miscellaneous exercise on this page. The Class 12 Maths chapter 6 miscellaneous exercise solutions are designed to make the students understand the applications of concepts studies in the NCERT book. Class 12 Maths chapter 6 miscellaneous solutions covers all the topics discussed in the previous exercises. Miscellaneous exercise chapter 6 Class 12 presents questions to practice the complete chapter.

This Story also Contains
  1. NCERT Solutions For Class 12 Chapter 6 Miscellaneous Exercise
  2. Application of Derivatives Miscellaneous Exercise
  3. More About NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise
  4. Key Features Of NCERT Solutions For Class 12 Chapter 6 Miscellaneous Exercise
  5. NCERT Solutions Subject Wise
  6. Subject Wise NCERT Exemplar Solutions

After completing all the topics of NCERT syllabus Class 12 Maths chapter 6 and solved and unsolved questions of all other exercises the miscellaneous exercise can be attempted. The miscellaneous exercise combines questions from the complete chapter and the level of questions compared to exercises will be a bit higher. Miscellaneous exercise class 12 chapter 5 are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise enumerated in NCERT Book together using the link provided below.

VMC VIQ Scholarship Test

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Apply
Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

Apply

Application of Derivatives Miscellaneous Exercise

Question:1(a) Using differentials, find the approximate value of each of the following:

( 17/81) ^{1/4 }

Answer:

Let y = x^\frac{1}{4} and x = \frac{16}{81} \ and \ \Delta x = \frac{1}{81}
\Delta y = (x+\Delta x)^\frac{1}{4}-x^\frac{1}{4}
= (\frac{16}{81}+\frac{1}{81})^\frac{1}{4}-(\frac{16}{81})^\frac{1}{4}
(\frac{17}{81})^\frac{1}{4} = \Delta y + \frac{2}{3}
Now, we know that \Delta y is approximate equals to dy
So,
dy = \frac{dy}{dx}.\Delta x \\ = \frac{1}{4x^\frac{3}{4}}.\frac{1}{81} \ \ \ \ \ \ \ (\because y = x^\frac{1}{4} \ and \ \Delta x = \frac{1}{81})\\ = \frac{1}{4(\frac{16}{81})^\frac{3}{4}}.\frac{1}{81} = \frac{27}{4\times 8}.\frac{1}{81} = \frac{1}{96}
Now,
(\frac{17}{81})^\frac{1}{4} = \Delta y + \frac{2}{3} = \frac{1}{96}+\frac{2}{3} = \frac{65}{96} = 0.677
Hence, (\frac{17}{81})^\frac{1}{4} is approximately equal to 0.677

Question:1(b) Using differentials, find the approximate value of each of the following:
( 33) ^{-1/5 }

Answer:

Let y = x^\frac{-1}{5} and x = 32 \ and \ \Delta x = 1
\Delta y = (x+\Delta x)^\frac{-1}{5}-x^\frac{-1}{5}
= (32+1)^\frac{-1}{5}-(32)^\frac{-1}{5}
(33)^\frac{-1}{4} = \Delta y + \frac{1}{2}
Now, we know that \Delta y is approximately equals to dy
So,
dy = \frac{dy}{dx}.\Delta x \\ = \frac{-1}{5x^\frac{6}{5}}.1 \ \ \ \ \ \ \ (\because y = x^\frac{-1}{5} \ and \ \Delta x = 1)\\ = \frac{-1}{5(32)^\frac{6}{5}}.1 = \frac{-1}{5\times 64}.1= \frac{-1}{320}
Now,
(33)^\frac{-1}{5} = \Delta y + \frac{1}{2} = \frac{-1}{320}+\frac{1}{2} = \frac{159}{320} = 0.497
Hence, (33)^\frac{-1}{5} is approximately equals to 0.497

Question:2. Show that the function given by f ( x ) = \frac{\log x}{x} has maximum at x = e.

Answer:

Given function is
f ( x ) = \frac{\log x}{x}
f^{'}(x) = \frac{1}{x}.\frac{1}{x} + log x\frac{-1}{x^2} = \frac{1}{x^2}(1-\log x)
f^{'}(x) =0 \\ \frac{1}{x^2}(1-\log x) = 0\\ \frac{1}{x^2} \neq 0 \ So \ log x = 1\Rightarrow x = e
Hence, x =e is the critical point
Now,
f^{''}(x) = \frac{-2x}{x^3}(1-\log x)+\frac{1}{x^2}(-\frac{1}{x}) = \frac{1}{x^3}(-2x+2xlog x-1)\\ f^{''(e)} = \frac{-1}{e^3} < 0
Hence, x = e is the point of maxima

Question:3 . The two equal sides of an isosceles triangle with fixed base b are decreasing at the rate of 3 cm per second. How fast is the area decreasing when the two equal sides are equal to the base ?

Answer:

It is given that the base of the triangle is b
and let the side of the triangle be x cm , \frac{dx}{dt} = -3 cm/s
We know that the area of the triangle(A) = \frac{1}{2}bh
now, h = \sqrt{x^2-(\frac{b}{2})^2}
A= \frac{1}{2}b \sqrt{x^2-(\frac{b}{2})^2}
\frac{dA}{dt}=\frac{dA}{dx}.\frac{dx}{dt}= \frac{1}{2}b\frac{2x}{2\sqrt{x^2-(\frac{b}{2})^2}}.(-3)
Now at x = b
\frac{dA}{dx} = \frac{1}{2}b\frac{2b}{\frac{\sqrt3b}{2}}.(-3)=-\sqrt3b
Hence, the area decreasing when the two equal sides are equal to the base is \sqrt3b cm^2/s

Question:4 Find the equation of the normal to curve x ^2 = 4 y which passes through the point (1, 2).

Answer:

Given the equation of the curve
x^2 = 4 y
We know that the slope of the tangent at a point on the given curve is given by \frac{dy}{dx}
4\frac{dy}{dx} = 2x \\\ \frac{dy}{dx} = \frac{x}{2}
We know that
Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent } = \frac{-1}{\frac{x}{2}} = \frac{-2}{x}
At point (a,b)
Slope = \frac{-2}{a}
Now, the equation of normal with point (a,b) and Slope = \frac{-2}{a}

y-y_1=m(x-x_1)\\ y-b=\frac{-2}{a}(x-a)
It is given that it also passes through the point (1,2)
Therefore,
2-b=\frac{-2}{a}(1-a)\\ 2a -ba = 2a -2\\ ba = 2\\b =\frac{2}{a} -(i)
It also satisfies equation x^2 = 4 y\Rightarrow b = \frac{a^2}{4} -(ii)
By comparing equation (i) and (ii)
\frac{2}{a} = \frac{a^2}{4}\\ a^3 = 8\\ a = 2
b = \frac{2}{a} = \frac{2}{2} = 1
Slope = \frac{-2}{a} = \frac{-2}{2} = -1

Now, equation of normal with point (2,1) and slope = -1

y-y_1=m(x-x_1)\\ y-1=-1(x-2)\\ y+x=3
Hence, equation of normal is x + y - 3 = 0

Question:5 . Show that the normal at any point \theta to the curve x = a \cos \theta + a \theta \sin \theta , y = a \sin \theta - a\theta \cos\theta is at a constant distance from the origin.

Answer:

We know that the slope of tangent at any point is given by \frac{dy}{dx}
Given equations are
x = a \cos \theta + a \theta \sin \theta , y = a \sin \theta - a\theta \cos\theta
\frac{dx}{d\theta} = -a\sin \theta + a\sin \theta -a\theta\cos \theta = -a\theta\cos \theta
\frac{dy}{d\theta} =a\cos \theta -a\cos \theta +a\theta (-\sin \theta) = -a\theta\sin \theta
\frac{dy}{dx} = \frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}} = \frac{-a\theta\sin \theta}{-a\theta \cos \theta} = \tan \theta
We know that
Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent} = \frac{-1}{\tan \theta}
equation of normal with given points and slope
y_2-y_1=m(x_2-x_1)\\ y - a\sin \theta + a\theta\cos\theta = \frac{-1}{\tan \theta}(x-a\cos\theta-a\theta\sin\theta)\\ y\sin\theta - a\sin^2 \theta + a\theta\cos\theta\sin\theta = -x\cos\theta+a\cos^2\theta+a\theta\sin\theta\cos\theta\\ y\sin\theta + x\cos\theta = a
Hence, the equation of normal is y\sin\theta + x\cos\theta = a
Now perpendicular distance of normal from the origin (0,0) is
D = \frac{|(0)\sin\theta+(0)\cos\theta-a|}{\sqrt{\sin^2\theta+\cos^2\theta}} = |-a| = a = \ constant \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\\ (\because \sin^2x+\cos^2x=1)
Hence, by this, we can say that

the normal at any point \theta to the curve x = a \cos \theta + a \theta \sin \theta , y = a \sin \theta - a\theta \cos\theta

is at a constant distance from the origin

Question:6(i) Find the intervals in which the function f given by f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x } is

increasing

Answer:

Given function is
f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }
f^{'}(x) = \frac{(4\cos x - 2-\cos x+x\sin x)(2+\cos x)-(4\sin x - 2x - x\cos x )(-\sin x)}{(2+\cos x)^2}
=\frac{4\cos x - \cos^2x}{2+\cos x}
f^{'}(x)=0\\ \frac{4\cos x - \cos^2x}{2+\cos x} =0\\ \cos x(4-\cos x) = 0\\ \cos x = 0 \ \ \ \ \ \ \ and \ \ \ \ \ \ \ \ \ \ \ \cos x =4
But \cos x \neq 4
So,
\cos x = 0 \\ x = \frac{\pi}{2} \ and \ \frac{3\pi}{2}
Now three ranges are there \left ( 0,\frac{\pi}{2} \right ),\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )
In interval \left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right ) , f^{'}(x) > 0

Hence, the given function f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x } is increasing in the interval \left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )
in interval ,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ), f^{'}(x) < 0 so function is decreasing in this inter

Question:6(ii) Find the intervals in which the function f given by f x is equal to

f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x } is

decreasing

Answer:

Given function is
f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x }
f^{'}(x) = \frac{(4\cos x - 2-\cos x+x\sin x)(2+\cos x)-(4\sin x - 2x - x\cos x )(-\sin x)}{(2+\cos x)^2}
=\frac{4\cos x - \cos^2x}{2+\cos x}
f^{'}(x)=0\\ \frac{4\cos x - \cos^2x}{2+\cos x} =0\\ \cos x(4-\cos x) = 0\\ \cos x = 0 \ \ \ \ \ \ \ and \ \ \ \ \ \ \ \ \ \ \ \cos x =4
But \cos x \neq 4
So,
\cos x = 0 \\ x = \frac{\pi}{2} \ and \ \frac{3\pi}{2}
Now three ranges are there \left ( 0,\frac{\pi}{2} \right ),\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )
In interval \left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right ) , f^{'}(x) > 0

Hence, given function f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x } is increasing in interval \left ( 0,\frac{\pi}{2} \right ) \ and \ \left ( \frac{3\pi}{2},2\pi \right )
in interval ,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right ), f^{'}(x) < 0
Hence, given function f (x) = \frac{4 \sin x - 2x - x \cos x }{2 + \cos x } is decreasing in interval ,\left ( \frac{\pi}{2},\frac{3\pi}{2} \right )

Question:7(i) Find the intervals in which the function f given by f (x) = x ^3 + \frac{1}{x^3}, x \neq 0

Increasing

Answer:

Given function is
f (x) = x ^3 + \frac{1}{x^3}
f^{'} (x) = 3x ^2 + \frac{-3x^2}{x^4}\\ f^{'}(x) = 0\\ 3x ^2 + \frac{-3x^2}{x^4} = 0\\ x^4 = 1\\ x = \pm1
Hence, three intervals are their (-\infty,-1),(-1,1) \ and (1,\infty)
In interval (-\infty,-1) \ and \ (1,\infty) , f^{'})x > 0
Hence, given function f (x) = x ^3 + \frac{1}{x^3} is increasing in interval (-\infty,-1) \ and \ (1,\infty)
In interval (-1,1) , f^{'}(x)< 0
Hence, given function f (x) = x ^3 + \frac{1}{x^3} is decreasing in interval (-1,1)

Question:7(ii) Find the intervals in which the function f given by f ( x) = x ^3 + \frac{1}{x^3} , x \neq 0

decreasing

Answer:

Given function is
f (x) = x ^3 + \frac{1}{x^3}
f^{'} (x) = 3x ^2 + \frac{-3x^2}{x^4}\\ f^{'}(x) = 0\\ 3x ^2 + \frac{-3x^2}{x^4} = 0\\ x^4 = 1\\ x = \pm1
1654666897895 Hence, three intervals are their (-\infty,-1),(-1,1) \ and (1,\infty)
In interval (-\infty,-1) \ and \ (1,\infty) , f^{'})x > 0
Hence, given function f (x) = x ^3 + \frac{1}{x^3} is increasing in interval (-\infty,-1) \ and \ (1,\infty)
In interval (-1,1) , f^{'}(x)< 0
Hence, given function f (x) = x ^3 + \frac{1}{x^3} is decreasing in interval (-1,1)

Question:8 Find the maximum area of an isosceles triangle inscribed in the ellipse \frac{x ^2 }{a^2}+ \frac{y^2}{b^2 } = 1 with its vertex at one end of the major axis.

Answer:

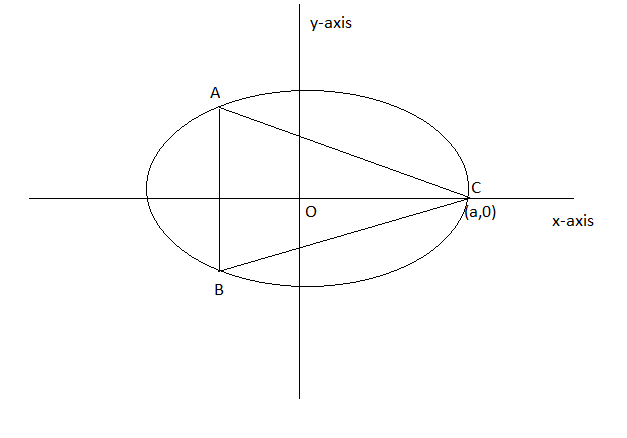
1628072034896 Given the equation of the ellipse
\frac{x ^2 }{a^2}+ \frac{y^2}{b^2 } = 1
Now, we know that ellipse is symmetrical about x and y-axis. Therefore, let's assume coordinates of A = (-n,m) then,
Now,
Put(-n,m) in equation of ellipse
we will get
m = \pm \frac{b}{a}.\sqrt{a^2-n^2}
Therefore, Now
Coordinates of A = \left ( -n,\frac{b}{a}.\sqrt{a^2-n^2} \right )
Coordinates of B = \left ( -n,-\frac{b}{a}.\sqrt{a^2-n^2} \right )
Now,
Length AB(base) = 2\frac{b}{a}.\sqrt{a^2-n^2}
And height of triangle ABC = (a+n)
Now,
Area of triangle = \frac{1}{2}bh
A = \frac{1}{2}.\frac{2b}{a}.\sqrt{a^2-n^2}.(a+n)= ab\sqrt{a^2-n^2}+bn\sqrt{a^2-n^2}
Now,
\frac{dA}{dn} = \frac{-abn}{\sqrt{a^2-n^2}}+n\sqrt{a^2-n^2}-\frac{bn^2}{\sqrt{a^2-n^2}}
Now,
\frac{dA}{dn} =0\\ \frac{-abn}{\sqrt{a^2-n^2}}+n\sqrt{a^2-n^2}-\frac{bn^2}{\sqrt{a^2-n^2}} =0\\ -abn + n(a^2-n^2)-bn^2 = 0\\ \Rightarrow n = -a,\frac{a}{2}
but n cannot be zero
therefore, n = \frac{a}{2}
Now, at n = \frac{a}{2}
\frac{d^2A}{dn^2}< 0
Therefore, n = \frac{a}{2} is the point of maxima
Now,
b = 2\frac{b}{a}.\sqrt{a^2- (\frac{a}{2})^2}= \sqrt3b
h = (a+ n ) = a+ \frac{ a}{2} = \frac{ 3a}{2}
Now,
Therefore, Area (A) = \frac{1}{2}bh = \frac{1}{2}\sqrt3 b \frac{3a}{2} = \frac{3\sqrt3ab}{4}

Question:9 A tank with rectangular base and rectangular sides, open at the top is to be constructed so that its depth is 2 m and volume is 8 m3. If building of tank costs Rs 70 per sq metres for the base and Rs 45 per square metre for sides. What is the cost of least expensive tank?

Answer:

Let l , b and h are length , breath and height of tank
Then, volume of tank = l X b X h = 8 m^3
h = 2m (given)
lb = 4 = l = \frac{4}{b}
Now,
area of base of tank = l X b = 4
area of 4 side walls of tank = hl + hl + hb + hb = 2h(l + b)
Total area of tank (A) = 4 + 2h(l + b)
A(b) = 4 + 2h(\frac{4}{b}+b)
A^{'}(b) = 2h(\frac{-4}{b^2}+1)\\ A^{'}(b)=0\\ 2h(\frac{-4}{b^2}+1) = 0\\ b^2= 4\\ b = 2
Now,
A^{''}(b) = 2h(\frac{-4\times-2b}{b^3})\\ A^{''}(2) = 8 > 0
Hence, b = 2 is the point of minima
l = \frac{4}{b} = \frac{4}{2} = 2
So, l = 2 , b = 2 and h = 2 m
Area of base = l X B = 2 X 2 = 4 \ m^2
building of tank costs Rs 70 per sq metres for the base
Therefore, for 4 \ m^2 Rs = 4 X 70 = 280 Rs
Area of 4 side walls = 2h(l + b)
= 2 X 2(2 + 2) = 16 \ m^2
building of tank costs Rs 45 per square metre for sides
Therefore, for 16 \ m^2 Rs = 16 X 45 = 720 Rs
Therefore, total cost for making the tank is = 720 + 280 = 1000 Rs

Question:10 The sum of the perimeter of a circle and square is k, where k is some constant. Prove that the sum of their areas is least when the side of square is double the radius of the circle.

Answer:

It is given that
the sum of the perimeter of a circle and square is k = 2\pi r + 4a = k\Rightarrow a = \frac{k - 2\pi r}{4}
Let the sum of the area of a circle and square(A) = \pi r^2 + a^2
A = \pi r^2 + (\frac{k-2\pi r}{4})^2
A^{'}(r) = 2\pi r + 2(\frac{k-2\pi r}{16})(- 2\pi)\\ A^{'}(r) = 0\\ 2\pi (\frac{8r-k-2\pi r}{8}) = 0\\ r = \frac{k}{8-2\pi}
Now,
A^{''}(r) = 2\pi (\frac{8-2\pi }{8}) = 0\\ A^{''}(\frac{k}{8-2\pi}) > 0
Hence, r= \frac{k}{8-2\pi} is the point of minima
a = \frac{k-2\pi r}{4} = \frac{k-2\pi \frac{k}{8-2\pi}}{4}=2 \frac{k}{8-2\pi} = 2r
Hence proved that the sum of their areas is least when the side of the square is double the radius of the circle

Question:11 A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.

Answer:

Let l and bare the length and breadth of rectangle respectively and r will be the radius of circle (r = \frac{l}{2})
The total perimeter of window = perimeter of rectangle + perimeter of the semicircle

= l+2b + \pi \frac{l}{2}
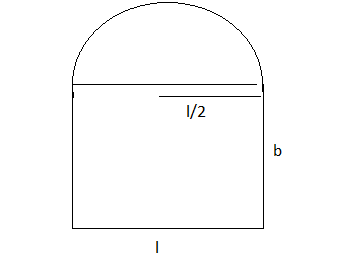
1628072096595
l+2b + \pi \frac{l}{2} = 10\\ l = \frac{2(10-2b)}{2+\pi}
Area of window id given by (A) = lb + \frac{\pi}{2}\left ( \frac{l}{2} \right )^2
= \frac{2(10-2b)}{2+\pi}b + \frac{\pi}{2}\left ( \frac{10-2b}{2+\pi} \right )^2\\
A^{'}(b) = \frac{20-8b}{2+\pi}+\frac{\pi}{2}.2(\frac{10-2b}{2+\pi}).\frac{(-2)}{2+\pi}
= \frac{20-8b}{2+\pi}-2\pi(\frac{10-2b}{(2+\pi)^2})\\ A^{'}(b) = 0\\ \frac{20-8b}{2+\pi}=2\pi(\frac{10-2b}{(2+\pi)^2})\\ 40 + 20\pi -16b -8\pi b = 20\pi - 4\pi b\\ 40 = 4b(\pi+4)\\b = \frac{10}{\pi+4}
Now,
A^{''}(b) = \frac{-8}{2+\pi}+\frac{4\pi}{(2+\pi)^2} = \frac{-16-8\pi+4\pi}{(2+\pi)^2} = \frac{-16-4\pi}{(2+\pi)^2} \\ A^{''}(\frac{10}{\pi+4}) < 0
Hence, b = 5/2 is the point of maxima
l = \frac{2(10-2b)}{2+\pi} = \frac{2(10-2.\frac{10}{4+\pi})}{2+\pi} = \frac{20}{4+\pi}
r= \frac{l}{2}= \frac{20}{2(4+\pi)}=\frac{10}{4+\pi}
Hence, these are the dimensions of the window to admit maximum light through the whole opening

Question:12 A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is ( a ^{\frac{2}{3}}+ b ^\frac{2}{3}) ^ \frac{3}{2}

Answer:

It is given that
A point on the hypotenuse of a triangle is at a distance a and b from the sides of the triangle

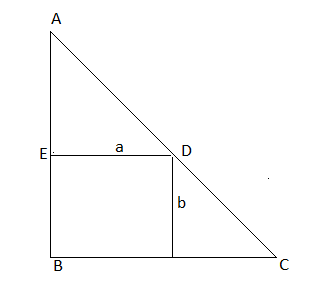1628072130108 Let the angle between AC and BC is \theta
So, the angle between AD and ED is also \theta
Now,
CD = b \ cosec\theta
And
AD = a \sec\theta
AC = H = AD + CD
= a \sec\theta + b \ cosec\theta
\frac{dH}{d\theta} = a \sec\theta\tan\theta - b\cot\theta cosec \theta\\ \frac{dH}{d\theta} = 0\\ a \sec\theta\tan\theta - b\cot\theta cosec \theta =0\\ a \sec\theta\tan\theta = b\cot\theta cosec \theta\\ a\sin^3\theta = b\cos^3\theta\\ \tan^3\theta = \frac{b}{a} \\ \tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3}
Now,
\frac{d^2H}{d\theta^2} > 0
When \tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3}
Hence, \tan\theta = \left ( \frac{b}{a} \right )^\frac{1}{3} is the point of minima
\sec \theta = \frac{a\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{a^\frac{1}{3}} and cosec \theta = \frac{b\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{b^\frac{1}{3}}

AC = \frac{a\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{a^\frac{1}{3}} + \frac{b\sqrt{a^\frac{2}{3}+b^\frac{2}{3}}}{b^\frac{1}{3}} = (a^\frac{2}{3}+b^\frac{2}{3})^\frac{3}{2}
Hence proved

Question:13 Find the points at which the function f given by f(x) = (x-2)^4(x+1)^3 has (i) local maxima (ii) local minima (iii) point of inflexion

Answer:

Given function is
f(x) = (x-2)^4(x+1)^3
f^{'}(x) = 4(x-2)^3(x+1)^3 + 3(x+1)^2(x-2)^4\\ f^{'}(x)= 0\\ 4(x-2)^3(x+1)^3 + 3(x+1)^2(x-2)^4=0\\ (x-2)^3(x+1)^2(4(x+1) + 3(x-2))\\ x = 2 , x = -1 \ and \ x = \frac{2}{7}
Now, for value x close to \frac{2}{7} and to the left of \frac{2}{7} , f^{'}(x) > 0 ,and for value close to \frac{2}{7} and to the right of \frac{2}{7} f^{'}(x) < 0
Thus, point x = \frac{2}{7} is the point of maxima
Now, for value x close to 2 and to the Right of 2 , f^{'}(x) > 0 ,and for value close to 2 and to the left of 2 f^{'}(x) < 0
Thus, point x = 2 is the point of minima
There is no change in the sign when the value of x is -1
Thus x = -1 is the point of inflexion

Question:14 Find the absolute maximum and minimum values of the function f given by
f (x) = \cos ^2 x + \sin x , x \epsilon [ 0 , \pi ]

Answer: Given function is
f (x) = \cos ^2 x + \sin x
f^{'} (x) = 2\cos x(-\sin x) + \cos x \\ f^{'}(x) = 0\\ -2\cos x\sin x + \cos x=0\\ \cos x(1-2\sin x) = 0\\ either\\ \cos x = 0 \ \ \ \ \ \ and \ \ \ \ \ \ \ \sin x = \frac{1}{2} \\ x = \frac{\pi}{2} \ \ \ \ \ \ \ \ \ \ and \ \ \ \ \ \ \ \ \ \ x = \frac{\pi}{6} \ \ \ \ \ as \ x \ \epsilon [0,\pi]
Now,
f^{''} (x) = -2(-\sin x)\sin x - 2\cos x\cos x + (-\sin x) \\ f^{''}(x)= 2\sin^2x - 2\cos^2x - \sin x\\ f^{''}(\frac{\pi}{6}) = \frac{-3}{2} < 0
Hence, the point x = \frac{\pi}{6} is the point of maxima and the maximum value is
f (\frac{\pi}{6}) = \cos ^2 \frac{\pi}{6} + \sin \frac{\pi}{6} = \frac{3}{4}+\frac{1}{2} = \frac{5}{4}
And
f^{''}(\frac{\pi}{2}) = 1 > 0
Hence, the point x = \frac{\pi}{2} is the point of minima and the minimum value is
f (\frac{\pi}{2}) = \cos ^2 \frac{\pi}{2} + \sin \frac{\pi}{2} =0 + 1 = 1

Question:15 Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is 4r/3

Answer:

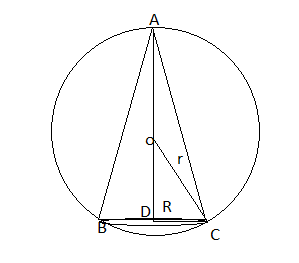1628072169934 The volume of a cone (V) = \frac{1}{3}\pi R^2h
The volume of the sphere with radius r = \frac{4}{3}\pi r^3
By Pythagoras theorem in \Delta ADC we ca say that
OD^2 = r^2 - R^2 \\ OD = \sqrt{r^2 - R^2}\\ h = AD = r + OD = r + \sqrt{r^2 - R^2}
V = \frac{1}{3}\pi R^2 (r + \sqrt{r^2+R^2})\\ = \frac{1}{3}\pi R^2r + \frac{1}{3}\pi R^2 \sqrt{r^2+R^2}
\frac{1}{3}\pi R^2 (r + \sqrt{r^2-R^2})\\ V^{'}(R)= \frac{2}{3}\pi Rr + \frac{2}{3}\pi R \sqrt{r^2-R^2}+\frac{1}{3}\pi R^2.\frac{-2R}{2\sqrt{r^2-R^2}}\\ V^{'}(R) = 0\\ \frac{1}{3}\pi R \left ( 2r + 2\sqrt{r^2-R^2} - \frac{R^2}{\sqrt{r^2-R^2}} \right ) = 0\\ \frac{1}{3}\pi R \left ( \frac{2r\sqrt{r^2-R^2} + 2r^2-2R^2 -R^2}{\sqrt{r^2-R^2}} \right ) = 0\\ R \neq 0 \ So, \\ 2r\sqrt{r^2-R^2} = 3R^2 - 2r^2\\ Square \ both \ sides\\ 4r^4-4r^2R^2 = 9R^4 + 4r^4 - 12R^2r^2\\ 9R^4-8R^2r^2 = 0\\ R^2(9R^2-8r^2) = 0\\ R \neq 0 \ So, 9R^2 = 8r^2\\ R = \frac{2\sqrt2r}{3}
Now,
V^{''}(R)= \frac{2}{3}\pi r + \frac{2}{3}\pi \sqrt{r^2-R^2}+\frac{2}{3}\pi R.\frac{-2R}{2\sqrt{r^2-R^2}}-\frac{3\pi R^2}{\sqrt{r^2-R^2}} - \frac{(-1)(-2R)}{(r^2+R^2)\frac{3}{2}}\\ V^{''}(\frac{2\sqrt2r}{3}) < 0
Hence, the point R = \frac{2\sqrt2r}{3} is the point of maxima
h = r + \sqrt{r^2-R^2} = r + \sqrt{r^2-\frac{8r^2}{9}} = r + \frac{r}{3} = \frac{4r}{3}
Hence, the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is \frac{4r}{3}

Question:16 Let f be a function defined on [a, b] such that f (x) > 0 , for all x \: \: \epsilon \: \: ( a,b) . Then prove that f is an increasing function on (a, b).

Answer:

Let's do this question by taking an example
suppose
f(x)= x^3 > 0 , (a.b)
Now, also
f{'}(x)= 3x^2 > 0 , (a,b)
Hence by this, we can say that f is an increasing function on (a, b)

Question:17 Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is \frac{2 R }{\sqrt 3 } . Also, find the maximum volume.

Answer:

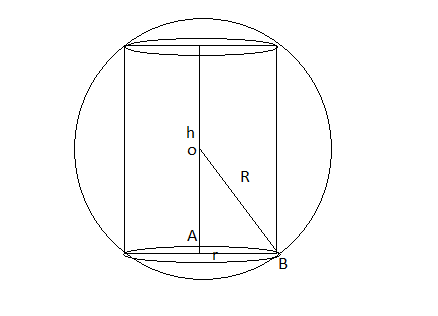1628072213939 The volume of the cylinder (V) = \pi r^2 h
By Pythagoras theorem in \Delta OAB
OA = \sqrt{R^2-r^2}
h = 2OA
h = 2\sqrt{R^2-r^2}
V = 2\pi r^2\sqrt{R^2-r^2}
V^{'}(r) = 4\pi r\sqrt{R^2-r^2}+2\pi r^2 . \frac{-2r}{2\sqrt{R^2-r^2}}\\ V^{'}(r) = 0\\ 4\pi r\sqrt{R^2-r^2}- \frac{2\pi r^3}{\sqrt{R^2-r^2}} = 0\\ 4\pi r (R^2-r^2 ) - 2\pi r^3 = 0\\ 6\pi r^3 = 4\pi rR^2\\ r =\frac{\sqrt6R}{3}
Now,
V^{''}(r) = 4\pi \sqrt{R^2-r^2}+4\pi r.\frac{-2r}{2\sqrt{R^2-r^2}}- \frac{6\pi r^2}{\sqrt{R^2-r^2}}.\frac{(-1)-2r}{2(R^2-r^2)\frac{3}{2}}\\ V^{''}(\frac{\sqrt6R}{3}) < 0
Hence, the point r = \frac{\sqrt6R}{3} is the point of maxima
h = 2\sqrt{R^2-r^2} = = 2\sqrt{R^2 - \frac{2R^2}{3}} =\frac{2R}{\sqrt3}
Hence, the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is \frac{2 R }{\sqrt 3 }
and maximum volume is
V = \pi r^2 h = \pi \frac{2R^2}{3}.\frac{2R}{\sqrt3} = \frac{4\pi R^3}{3\sqrt3}

Question:18 Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle a is one-third that of the cone and the greatest volume of cylinder is

\frac{4}{27}\pi h ^3 \tan ^2 \alpha

Answer:

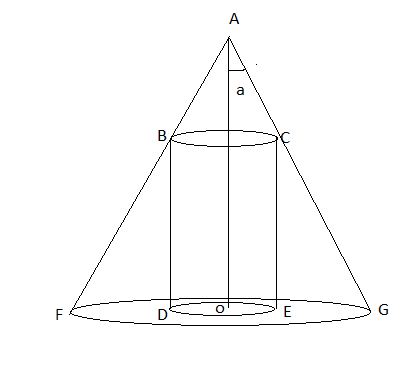1628072251851 Let's take radius and height of cylinder = r and h ' respectively
Let's take radius and height of cone = R and h respectively

Volume of cylinder = \pi r^2 h'
Volume of cone = \frac{1}{3}\pi R^2 h
Now, we have
R = h\tan a
Now, since \Delta AOG \and \Delta CEG are similar
\frac{OA}{OG} = \frac{CE}{EG}
\frac{h}{R} = \frac{h'}{R-r}
h'=\frac{h(R-r)}{R}
h'=\frac{h(h\tan a-r)}{h\tan a} = \frac{h\tan a- r}{\tan a}
Now,
V = \pi r^ 2 h' = \pi r^2 .\frac{h\tan a-r}{\tan a} = \pi r^2 h - \frac{\pi r^3}{\tan a}
Now,
\frac{dV}{dr}= 2\pi rh- \frac{3\pi r^2}{\tan a} \\ \frac{dV}{dr}=0\\ 2\pi rh- \frac{3\pi r^2}{\tan a} = 0\\ 2\pi rh = \frac{3\pi r^2}{\tan a}\\ r = \frac{2h\tan a}{3}
Now,
\frac{d^2V}{dr^2}= 2\pi h- \frac{6\pi r}{\tan a}
at r = \frac{2h\tan a}{3}
\frac{d^2V}{dr^2} = 2\pi h- 4\pi h < 0
Hence, r = \frac{2h\tan a}{3} is the point of maxima
h' = \frac{h\tan a-r}{\tan a} = \frac{h\tan a- \frac{2h\tan a}{3}}{\tan a}= \frac{1}{3}h
Hence proved
Now, Volume (V) at h' = \frac{1}{3}h and r = \frac{2h\tan a}{3} is
V = \pi r^2 h' = \pi \left ( \frac{2h\tan a}{3} \right )^2.\frac{h}{3}= \frac{4}{27}.\pi h^3\tan^2 a
hence proved

Question:19 A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314
cubic metre per hour. Then the depth of the wheat is increasing at the rate of

(A) 1 m/h

(B) 0.1 m/h

(C) 1.1 m/h

(D) 0.5 m/h

Answer:

It is given that
\frac{dV}{dt} = 314 \ m^3/h
Volume of cylinder (V) = \pi r^2 h = 100\pi h \ \ \ \ \ \ \ \ \ \ \ (\because r = 10 m)
\frac{dV}{dt} = 100\pi \frac{dh}{dt}\\ 314 = 100\pi \frac{dh}{dt}\\ \frac{dh}{dt} = \frac{3.14}{\pi} = 1 \ m/h
Hence, (A) is correct answer

Question:20 The slope of the tangent to the curve x = t^2 + 3t - 8, y = 2t^2 - 2t - 5 at the point
(2,– 1) is

A ) 22/7

B ) 6/7

C ) 7/6

D ) -6 /7

Answer:

Given curves are
x = t^2 + 3t - 8 \ and \ y = 2t^2 - 2t - 5
At point (2,-1)
t^2 + 3t - 8 = 2\\ t^2+3t-10=0\\ t^2+5t-2t-10=0\\ (t+5)(t-2) = 0\\ t = 2 \ and \ t = 5
Similarly,
2t^2-2t-5 = -1\\ 2t^2-2t-4=0\\ 2t^2-4t+2t-4=0\\ (2t+2)(t-2)=0\\ t = -1 \ and \ t = 2
The common value between two is t = 2
Hence, we find the slope of the tangent at t = 2
We know that the slope of the tangent at a given point is given by \frac{dy}{dx}
\frac{dy}{dt} = 4t - 2
\frac{dx}{dt} = 2t + 3
\left ( \frac{dy}{dx} \right )_{t=2} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} = \frac{4t-2}{2t+3} = \frac{8-2}{4+3} = \frac{6}{7}
Hence, (B) is the correct answer

Question:21 The line y is equal to is a tangent to the curve if the value of m is
(A) 1

(B) 2

(C) 3

(D)1/2

Answer:

Standard equation of the straight line
y = mx + c
Where m is lope and c is constant
By comparing it with equation , y = mx + 1
We find that m is the slope
Now,
we know that the slope of the tangent at a given point on the curve is given by \frac{dy}{dx}
Given the equation of the curve is
y^2 = 4x
2y\frac{dy}{dx} = 4\\ \frac{dy}{dx} = \frac{2}{y}
Put this value of m in the given equation
y = \frac{2}{y}.\frac{y^2}{4}+1 \ \ \ \ \ \ \ \ \ \ (\because y^2 = 4x \ and \ m =\frac{2}{y})\\ y = \frac{y}{2}+1\\ \frac{y}{2} = 1\\ y = 2
m = \frac{2}{y} = \frac{2}{2} = 1
Hence, value of m is 1
Hence, (A) is correct answer

Question:22 The normal at the point (1,1) on the curve 2y + x ^2 = 3 is
(A) x + y = 0

(B) x – y = 0

(C) x + y +1 = 0

(D) x – y = 1

Answer:

Given the equation of the curve
2y + x ^2 = 3
We know that the slope of the tangent at a point on the given curve is given by \frac{dy}{dx}
2\frac{dy}{dx} = -2x\\ \frac{dy}{dx} = -x
We know that
Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent } = \frac{-1}{-x} = \frac{1}{x}
At point (1,1)
Slope = \frac{1}{1} = 1
Now, the equation of normal with point (1,1) and slope = 1

y-y_1=m(x-x_1)\\ y-1=1(x-1)\\ x-y = 0
Hence, the correct answer is (B)

Question:23 The normal to the curve x^2 = 4 y passing (1,2) is

(A) x + y = 3

(B) x – y = 3

(C) x + y = 1

(D) x – y = 1

Answer:

Given the equation of the curve
x^2 = 4 y
We know that the slope of the tangent at a point on the given curve is given by \frac{dy}{dx}
4\frac{dy}{dx} = 2x \\\ \frac{dy}{dx} = \frac{x}{2}
We know that
Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent } = \frac{-1}{\frac{x}{2}} = \frac{-2}{x}
At point (a,b)
Slope = \frac{-2}{a}
Now, the equation of normal with point (a,b) and Slope = \frac{-2}{a}

?
It is given that it also passes through the point (1,2)
Therefore,
2-b=\frac{-2}{a}(1-a)\\ 2a -ba = 2a -2\\ ba = 2\\b =\frac{2}{a} -(i)
It also satisfies equation x^2 = 4 y\Rightarrow b = \frac{a^2}{4} -(ii)
By comparing equation (i) and (ii)
\frac{2}{a} = \frac{a^2}{4}\\ a^3 = 8\\ a = 2
b = \frac{2}{a} = \frac{2}{2} = 1
Slope = \frac{-2}{a} = \frac{-2}{2} = -1

Now, equation of normal with point (2,1) and slope = -1

y-y_1=m(x-x_1)\\ y-1=-1(x-2)\\ y+x=3
Hence, correct answer is (A)

Question:24 The points on the curve 9 y^2 = x ^3 , where the normal to the curve makes equal intercepts with the axes are

A ) \left ( 4 , \pm \frac{8}{3} \right )\\\\ .\: \: \: \: \: B ) \left ( 4 , \frac{-8}{3} \right ) \\\\ . \: \: \: \: \: C) \left ( 4 , \pm \frac{3}{8} \right ) \\\\ . \: \: \: \: D ) \left ( \pm 4 , \frac{3}{8} \right )

Answer:

Given the equation of the curve
9 y^2 = x ^3
We know that the slope of the tangent at a point on a given curve is given by \frac{dy}{dx}
18y\frac{dy}{dx} = 3x^2\\ \frac{dy}{dx} = \frac{x^2}{6y}
We know that
Slope \ of \ normal = \frac{-1}{Slope \ of \ tangent } = \frac{-1}{\frac{x^2}{6y}} = \frac{-6y}{x^2}
At point (a,b)
Slope = \frac{-6b}{a^2}
Now, the equation of normal with point (a,b) and Slope = \frac{-6b}{a^2}

y-y_1=m(x-x_1)\\ y-b=\frac{-6b}{a^2}(x-a)\\ ya^2 - ba^2 = -6bx +6ab\\ ya^2+6bx=6ab+a^2b\\ \frac{y}{\frac{6b+ab}{a}}+\frac{x}{\frac{6a+a^2}{6}} = 1
It is given that normal to the curve makes equal intercepts with the axes
Therefore,
\frac{6b+ab}{a}=\frac{6a+a^2}{6} \\ 6b(6 + a) =a^2( 6+a)\\ a^2 = 6b
point(a,b) also satisfy the given equation of the curve
9 b^2 = a ^3\\ 9(\frac{a^2}{6})^2 = a^3\\ 9.\frac{a^4}{36} = a^3\\ a = 4
9b^2 = 4^3\\ 9b^2 =64\\ b = \pm\frac{8}{3}
Hence, The points on the curve 9 y^2 = x ^3 , where the normal to the curve makes equal intercepts with the axes are \left ( 4,\pm\frac{8}{3} \right )
Hence, the correct answer is (A)

More About NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise

Practice questions related to all the 5 main topics covered in the Class 12 NCERT Mathematics chapter application of derivatives are covered in Class 12 Maths chapter 6 miscellaneous exercise solutions. All these solutions of miscellaneous exercise are detailed in this page and are solved by Mathematics experts. The NCERT solutions for Class 12 Maths chapter 6 miscellaneous exercise are given in detail and step by step manner.

Also Read| Application of Derivatives Class 12 Notes

Benefits of NCERT Solutions for Class 12 Maths Chapter 6 Miscellaneous Exercise

  • Class 12 Maths chapter 6 miscellaneous solutions can be used to prepare for board exam as well as copetitive exams to the admission for various engineering colleges across India.
  • The NCERT solutions for Class 12 Maths chapter 6 miscellaneous exercise helps in revising the whole chapter and also some basic derivatives.
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Key Features Of NCERT Solutions For Class 12 Chapter 6 Miscellaneous Exercise

  • Comprehensive Coverage: The solutions encompass all the topics covered in miscellaneous exercise class 12 chapter 6, ensuring a thorough understanding of the concepts.
  • Step-by-Step Solutions: In this class 12 chapter 6 maths miscellaneous solutions, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
  • Accuracy and Clarity: Solutions for class 12 maths miscellaneous exercise chapter 6 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
  • Conceptual Clarity: In this class 12 maths ch 6 miscellaneous exercise solutions, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
  • Inclusive Approach: Solutions for class 12 chapter 6 miscellaneous exercise cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
  • Relevance to Curriculum: The solutions for miscellaneous exercise class 12 chapter 6 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. What are the concepts to be covered to solve NCERT solutions for Class 12 Maths chapter 6 miscellaneous exercise?

Questions related to the tropics rate of change of quantities, approximation, increasing and decreasing functions, tangents and normals and maxima and minima are covered in Class 12 Maths chapter 6 miscellaneous solutions.

2. What is the number of questions covered in the miscellaneous exercise?

24 questions are present in Class 12 Maths chapter 6 miscellaneous exercise solutions

3. How many miscellaneous solved examples are there in NCERT Class 12 Mathematics book?

10 miscellaneous questions are solved in Class 12 NCERT Mathematics book.

4. How many exercises are covered in the NCERT chapter application of derivatives?

Including miscellaneous, there are 6 exercises. For more questions students can use NCERT exemplar.

5. In total how many solved examples are given in class 12 NCERT Maths chapter 6?

51 solved examples are given in the chapter 6 application of derivatives

6. What is covered in exercise 6.5?

The questions regarding maximum and minimum of a function using derivatives are covered in the class 12 maths exercise 6.5

7. In which exercise the questions related to approximation are covered?

Exercise 6.4 and a few questions of Class 12 Maths chapter 6 miscellaneous solutions covers the concept of approximation.

8. What are the two tests discussed in the topic maxima and minima?

The two tests discussed are the first derivative test and the second derivative test.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 12th Examination

Admit Card Date:04 October,2024 - 29 November,2024

National Institute of Open Schooling 10th examination

Admit Card Date:04 October,2024 - 29 November,2024

Mizoram Board of School Education 12th Examination

Application Date:07 October,2024 - 22 November,2024

Mizoram Board 10th Examination

Application Date:07 October,2024 - 22 November,2024

Punjab Board of Secondary Education 10th Examination

Application Correction Date:08 October,2024 - 27 November,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 812 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
IBM
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer
Jefferson 25 September,2024
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

  1. Re-evaluate Your Study Strategies:

    • Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
    • Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
    • Practice Regularly: Consistent practice is key to mastering chemistry.

  2. Consider Professional Help:

    • Tutoring: A tutor can provide personalized guidance and support.
    • Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.

  3. Explore Alternative Options:

    • Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
    • Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.

  4. Focus on NEET 2025 Preparation:

    • Stay Dedicated: Continue your NEET preparation with renewed determination.
    • Utilize Resources: Make use of study materials, online courses, and mock tests.

  5. Seek Support:

    • Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
    • Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.







Read Complete Answer
Kanishka kaushikii 17 September,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer
Yuvan 30 August,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 30th NOV'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View All Application Forms
News and Notifications
15 hours ago :
October 23, 2024 - 04:01 PM IST :
CBSE Board Exam Date Sheet 2025 (OUT) Live: CBSE Classes 10, 12 time table out 86 days before exams start
November 20, 2024 - 11:17 PM IST
CBSE Class 12 board exam date sheet 2025 out; exams from February 15 to April 4
November 20, 2024 - 09:56 PM IST
When will CBSE Board exam 2025 date sheet be released for Class 10, 12?
November 20, 2024 - 03:58 PM IST
CBSE Date Sheet 2025 Live: Class 10, 12 board exam dates soon; syllabus, sample papers
November 18, 2024 - 09:47 PM IST
Education News This Week: Fake news on CBSE exams; UPPSC protests, crackdown on coaching ads
November 17, 2024 - 01:51 PM IST
Extra time in CBSE exams for students with type 1 diabetes: Kerala SHRC seeks report on plea
November 16, 2024 - 09:45 PM IST
No changes in exam, IA system: CBSE rebuts claims of syllabus reduction, open book exams in 2025
November 14, 2024 - 07:31 PM IST

Stay up-to date with CBSE Class 12th News

Back to top