Careers360 Logo
School
Search Colleges, Exams, Schools & more
NCERT Solutions for Exercise 6.5 Class 12 Maths Chapter 6 - Application of Derivatives

NCERT Solutions for Exercise 6.5 Class 12 Maths Chapter 6 - Application of Derivatives

Edited By Ramraj Saini | Updated on Dec 03, 2023 08:53 PM IST | #CBSE Class 12th

NCERT Solutions For Class 12 Maths Chapter 6 Exercise 6.5

NCERT Solutions for Exercise 6.5 Class 12 Maths Chapter 6 Application of Derivatives are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Throughout the NCERT solutions for exercise 6.5 Class 12 Maths chapter 6 the topic maxima and minima is discussed. NCERT solutions for Class 12 Maths chapter 6 exercise 6.5 uses the concept of derivatives to find the maximum and minimum of different functions. Exercise 6.5 Class 12 Maths also give ideas about absolute minimum and maximum. In the NCERT Class 12 Mathematics Book, some real-life examples of finding maximum and minimum values are given. And certain definitions are discussed after the examples in the NCERT book. Such as definitions of maximum and minimum values, extreme point, monotonic functions, local maxima and minima and certain theorems etc. After these the Class 12 Maths chapter 6 exercise 6.5 is given for practice.

This Story also Contains
  1. NCERT Solutions For Class 12 Maths Chapter 6 Exercise 6.5
  2. Access NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5
  3. Application of Derivatives Exercise 6.5
  4. More About NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5
  5. Benefits of NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5
  6. Key Features Of NCERT Solutions for Exercise 6.5 Class 12 Maths Chapter 6
  7. NCERT Solutions Subject Wise
  8. Subject Wise NCERT Exemplar Solutions

12th class Maths exercise 6.5 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Also, read

VMC VIQ Scholarship Test

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Apply
Pearson | PTE

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer! Trusted by 3,500+ universities globally

Apply

Access NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5

Download PDF

Application of Derivatives Exercise 6.5

Question:1(i) Find the maximum and minimum values, if any, of the following functions
given by
( f (x) = (2x - 1)^2 + 3)

Answer:

Given function is,
f (x) = 9x^ 2 + 12x + 2
add and subtract 2 in given equation
f (x) = 9x^ 2 + 12x + 2 + 2- 2\\ f(x)= 9x^2 +12x+4-2\\ f(x)= (3x+2)^2 - 2
Now,
(3x+2)^2 \geq 0\\ (3x+2)^2-2\geq -2 for every x \ \epsilon \ R
Hence, minimum value occurs when
(3x+2)=0\\ x = \frac{-2}{3}
Hence, the minimum value of function f (x) = 9x^2+12x+2 occurs at x = \frac{-2}{3}
and the minimum value is
f(\frac{-2}{3}) = 9(\frac{-2}{3})^2+12(\frac{-2}{3})+2=4-8+2 =-2 \\

and it is clear that there is no maximum value of f (x) = 9x^2+12x+2

Question:1(ii) Find the maximum and minimum values, if any, of the following functions
given by

f (x) = 9x^ 2 + 12x + 2

Answer:

Given function is,
f (x) = 9x^ 2 + 12x + 2add and subtract 2 in given equation

f (x) = 9x^ 2 + 12x + 2 + 2- 2\\ f(x)= 9x^2 +12x+4-2\\ f(x)= (3x+2)^2 - 2

Now,(3x+2)^2 \geq 0\\ (3x+2)^2-2\geq -2 for every x \ \epsilon \ R

Hence, minimum value occurs when

(3x+2)=0\\ x = \frac{-2}{3}

Hence, the minimum value of function f (x) = 9x^2+12x+2 occurs at x = \frac{-2}{3}and the minimum value isf(\frac{-2}{3}) = 9(\frac{-2}{3})^2+12(\frac{-2}{3})+2=4-8+2 =-2 \\and it is clear that there is no maximum value of f (x) = 9x^2+12x+2

Question:1(iii) Find the maximum and minimum values, if any, of the following functions
given by

f (x) = - (x -1) ^2 + 10

Answer:

Given function is,
f (x) = - (x -1) ^2 + 10
-(x-1)^2 \leq 0\\ -(x-1)^2+10\leq 10 for every x \ \epsilon \ R
Hence, maximum value occurs when
(x-1)=0\\ x = 1
Hence, maximum value of function f (x) = - (x -1) ^2 + 10 occurs at x = 1
and the maximum value is
f(1) = -(1-1)^2+10=10 \\

and it is clear that there is no minimum value of f (x) = 9x^2+12x+2

Question:1(iv) Find the maximum and minimum values, if any, of the following functions
given by
g(x) = x^3 + 1

Answer:

Given function is,
g(x) = x^3 + 1
value of x^3 varies from -\infty < x^3 < \infty
Hence, function g(x) = x^3 + 1 neither has a maximum or minimum value

Question:2(i) Find the maximum and minimum values, if any, of the following functions
given by
f (x) = |x + 2| - 1

Answer:

Given function is
f (x) = |x + 2| - 1
|x+2| \geq 0\\ |x+2| - 1 \geq -1 x \ \epsilon \ R
Hence, minimum value occurs when |x + 2| = 0
x = -2
Hence, minimum value occurs at x = -2
and minimum value is
f(-2) = |-2+2| - 1 = -1
It is clear that there is no maximum value of the given function x \ \epsilon \ R

Question:2(ii) Find the maximum and minimum values, if any, of the following functions
given by
g(x) = - | x + 1| + 3

Answer:

Given function is
g(x) = - | x + 1| + 3
-|x+1| \leq 0\\ -|x+1| + 3 \leq 3 x \ \epsilon \ R
Hence, maximum value occurs when -|x + 1| = 0
x = -1
Hence, maximum value occurs at x = -1
and maximum value is
g(-1) = -|-1+1| + 3 = 3
It is clear that there is no minimum value of the given function x \ \epsilon \ R

Question:2(iii) Find the maximum and minimum values, if any, of the following functions
given by
h(x) = \sin(2x) + 5

Answer:

Given function is
h(x) = \sin(2x) + 5
We know that value of sin 2x varies from
-1 \leq sin2x \leq 1
-1 + 5 \leq sin2x +5\leq 1 +5\\ 4 \leq sin2x +5\leq 6
Hence, the maximum value of our function h(x) = \sin(2x) + 5 is 6 and the minimum value is 4

Question:2(iv) Find the maximum and minimum values, if any, of the following functions
given by
f (x) = | \sin 4x + 3|

Answer:

Given function is
f (x) = | \sin 4x + 3|
We know that value of sin 4x varies from
-1 \leq sin4x \leq 1
-1 + 3 \leq sin4x +3\leq 1 +3\\ 2 \leq sin4x +3\leq 4\\ 2\leq | sin4x +3| \leq 4
Hence, the maximum value of our function f (x) = | \sin 4x + 3| is 4 and the minimum value is 2

Question:2(v) Find the maximum and minimum values, if any, of the following functions
given by
h(x) = x + 1 , x \epsilon ( -1,1)

Answer:

Given function is
h(x) = x + 1
It is given that the value of x \ \epsilon (-1,1)
So, we can not comment about either maximum or minimum value
Hence, function h(x) = x + 1 has neither has a maximum or minimum value

Question:3(i) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:
f ( x) = x^2

Answer:

Given function is
f ( x) = x^2\\ f^{'}(x) = 2x\\ f^{'}(x) = 0 \Rightarrow 2x = 0 \Rightarrow x = 0
So, x = 0 is the only critical point of the given function
f^{'}(0) = 0\\ So we find it through the 2nd derivative test
f^{''}(x) = 2\\ f^{''}(0) = 2\\ f^{''}(0)> 0
Hence, by this, we can say that 0 is a point of minima
and the minimum value is
f(0) = (0)^2 = 0

Question:3(ii) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:
g(x) = x ^3 - 3x

Answer:

Given function is
g(x) = x ^3 - 3x\\ g^{'}(x) = 3x^2 - 3\\ g^{'}(x)=0\Rightarrow 3x^2-3 =0 \Rightarrow x = \pm 1\\
Hence, the critical points are 1 and - 1
Now, by second derivative test
g^{''}(x)=6x
g^{''}(1)=6 > 0
Hence, 1 is the point of minima and the minimum value is
g(1) = (1)^3 - 3(1) = 1 - 3 = -2
g^{''}(-1)=-6 < 0
Hence, -1 is the point of maxima and the maximum value is
g(1) = (-1)^3 - 3(-1) = -1 + 3 = 2

Question:3(iii) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:
h(x) = \sin x + \cos x,\ 0<x<\frac{\pi}{2}

Answer:

Given function is
h(x) = \sin x + \cos x\\ h^{'}(x)= \cos x - \sin x\\ h^{'}(x)= 0\\ \cos x - \sin x = 0\\ \cos x = \sin x\\ x = \frac{\pi}{4} \ \ \ \ \ \ as \ x \ \epsilon \ \left ( 0,\frac{\pi}{2} \right )
Now, we use the second derivative test
h^{''}(x)= -\sin x - \cos x\\ h^{''}(\frac{\pi}{4}) = -\sin \frac{\pi}{4} - \cos \frac{\pi}{4}\\ h^{''}(\frac{\pi}{4}) = -\frac{1}{\sqrt2}-\frac{1}{\sqrt2}\\ h^{''}(\frac{\pi}{4})= -\frac{2}{\sqrt2} = -\sqrt2 < 0
Hence, \frac{\pi}{4} is the point of maxima and the maximum value is h\left ( \frac{\pi}{4} \right ) which is \sqrt2

Question:3(iv) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

f(x) = sin x - cos x

Answer:

Given function is
h(x) = \sin x - \cos x\\ h^{'}(x)= \cos x + \sin x\\ h^{'}(x)= 0\\ \cos x + \sin x = 0\\ \cos x = -\sin x\\ x = \frac{3\pi}{4} \ \ \ \ \ \ as \ x \ \epsilon \ \left ( 0,2\pi \right )
Now, we use second derivative test
h^{''}(x)= -\sin x + \cos x\\ h^{''}(\frac{3\pi}{4}) = -\sin \frac{3\pi}{4} + \cos \frac{3\pi}{4}\\ h^{''}(3\frac{\pi}{4}) = -(\frac{1}{\sqrt2})-\frac{1}{\sqrt2}\\ h^{''}(\frac{\pi}{4})=- \frac{2}{\sqrt2} = -\sqrt2 < 0
Hence, \frac{\pi}{4} is the point of maxima and maximum value is h\left ( \frac{3\pi}{4} \right ) which is \sqrt2

Question:3(v) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

f (x) = x^3 - 6x^2 + 9x + 15

Answer:

Givrn function is
f (x) = x^3 - 6x^2 + 9x + 15\\ f^{'}(x) = 3x^2 - 12x + 9\\ f^{'}(x)= 0\\ 3x^2 - 12x + 9 = 0\\ 3(x^2-4x+3)=0\\ x^2-4x+3 = 0\\ x^2 - x -3x + 3=0\\ x(x-1)-3(x-1) = 0\\ (x-1)(x-3) = 0\\ x=1 \ \ \ \ \ \ and \ \ \ \ \ \ \ x = 3
Hence 1 and 3 are critical points
Now, we use the second derivative test
f^{''}(x) = 6x - 12\\ f^{''}(1) = 6 - 12 = -6 < 0
Hence, x = 1 is a point of maxima and the maximum value is
f (1) = (1)^3 - 6(1)^2 + 9(1) + 15 = 1-6+9+15 = 19
f^{''}(x) = 6x - 12\\ f^{''}(3) = 18 - 12 = 6 > 0
Hence, x = 1 is a point of minima and the minimum value is
f (3) = (3)^3 - 6(3)^2 + 9(3) + 15 = 27-54+27+15 = 15

Question:3(vi) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

g ( x) = \frac{x}{2} + \frac{2}{x} , x > 0

Answer:

Given function is
g ( x) = \frac{x}{2} + \frac{2}{x}\\ g^{'}(x) = \frac{1}{2}-\frac{2}{x^2}\\ g^{'}(x) = 0\\ \frac{1}{2}-\frac{2}{x^2} = 0\\ x^2 = 4\\ x = \pm 2

( but as x > 0 we only take the positive value of x i.e. x = 2)
Hence, 2 is the only critical point
Now, we use the second derivative test
g^{''}(x) = \frac{4}{x^3}\\ g^{''}(2) = \frac{4}{2^3} =\frac{4}{8} = \frac{1}{2}> 0
Hence, 2 is the point of minima and the minimum value is
g ( x) = \frac{x}{2} + \frac{2}{x} \\ g(2) = \frac{2}{2} + \frac{2}{2} = 1 + 1 = 2

Question:3(vii) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

g (x) = \frac{1}{x^2 + 2}

Answer:

Gien function is
g (x) = \frac{1}{x^2 + 2}\\ g^{'}(x) = \frac{-2x}{(x^2+2)^2}\\ g^{'}(x) = 0\\ \frac{-2x}{(x^2+2)^2} = 0\\ x = 0
Hence., x = 0 is only critical point
Now, we use the second derivative test
g^{''}(x) = -\frac{-2(x^2+2)^2-(-2x){2(x^2+2)(2x)}}{((x^2+2)^2)^2} \\ g^{''}(0) = \frac{-2\times4}{(2)^4} = \frac{-8}{16} = -\frac{1}{2}< 0
Hence, 0 is the point of local maxima and the maximum value is
g (0) = \frac{1}{0^2 + 2} = \frac{1}{2}

Question:3(viii) Find the local maxima and local minima, if any, of the following functions. Find
also the local maximum and the local minimum values, as the case may be:

f (x) = x \sqrt{ 1-x } , 0 < x < 1

Answer:

Given function is
f (x) = x \sqrt{ 1-x }
f ^{'}(x) = \sqrt{1-x} + \frac{x(-1)}{2\sqrt{1-x}}
= \sqrt{1-x} - \frac{x}{2\sqrt{1-x}} \Rightarrow \frac{2-3x}{2\sqrt{1-x}}\\ f^{'}(x) = 0\\ \frac{2-3x}{2\sqrt{1-x}} = 0\\ 3x = 2\\ x = \frac{2}{3}
Hence, x = \frac{2}{3} is the only critical point
Now, we use the second derivative test
f^{''}(x)= \frac{(-1)(2\sqrt{1-x})-(2-x)(2.\frac{-1}{2\sqrt{1-x}}(-1))}{(2\sqrt{1-x})^2}
= \frac{-2\sqrt{1-x}-\frac{2}{\sqrt{1-x}}+\frac{x}{\sqrt{1-x}}}{4(1-x)}
= \frac{3x}{4(1-x)\sqrt{1-x}}
f^{"}(\frac{2}{3}) > 0
Hence, it is the point of minima and the minimum value is
f (x) = x \sqrt{ 1-x }\\ f(\frac{2}{3}) = \frac{2}{3}\sqrt{1-\frac{2}{3}}\\ f(\frac{2}{3}) = \frac{2}{3}\sqrt{\frac{1}{3}}\\ f(\frac{2}{3}) = \frac{2}{3\sqrt3}\\ f(\frac{2}{3}) = \frac{2\sqrt3}{9}

Question:4(i) Prove that the following functions do not have maxima or minima:
f (x) = e ^x

Answer:

Given function is
f (x) = e ^x
f^{'}(x) = e^x\\ f^{'}(x) = 0\\ e^x=0\\
But exponential can never be 0
Hence, the function f (x) = e ^x does not have either maxima or minima

Question:4(ii) Prove that the following functions do not have maxima or minima:

g(x) = \log x

Answer:

Given function is
g(x) = \log x
g^{'}(x) = \frac{1}{x}\\ g^{'}(x) = 0\\ \frac{1}{x}= 0\\
Since log x deifne for positive x i.e. x > 0
Hence, by this, we can say that g^{'}(x)> 0 for any value of x
Therefore, there is no c \ \epsilon \ R such that g^{'}(c) = 0
Hence, the function g(x) = \log x does not have either maxima or minima

Question:4(iii) Prove that the following functions do not have maxima or minima:

h(x) = x^3 + x^2 + x +1

Answer:

Given function is
h(x) = x^3 + x^2 + x +1
h^{'}(x) = 3x^2+2x+1\\ h^{'}(x) = 0\\ 3x^2+2x+1 = 0\\ 2x^2+x^2+2x+1 = 0\\ 2x^2 + (x+1)^2 = 0\\
But, it is clear that there is no c \ \epsilon \ R such that f^{'}(c) = 0
Hence, the function h(x) = x^3 + x^2 + x +1 does not have either maxima or minima

Question:5(i) Find the absolute maximum value and the absolute minimum value of the following
functions in the given intervals:
f (x) = x ^ 3, x \epsilon [- 2, 2]

Answer:

Given function is
f(x) = x^3
f^{'}(x) = 3x^2\\ f^{'}(x) = 0\\ 3x^2 = 0\Rightarrow x = 0
Hence, 0 is the critical point of the function f(x) = x^3
Now, we need to see the value of the function f(x) = x^3 at x = 0 and as x \ \epsilon \ [-2,2]

we also need to check the value at end points of given range i.e. x = 2 and x = -2
f(0) = (0)^3 = 0\\ f(2= (2)^3 = 8\\ f(-2)= (-2)^3 = -8
Hence, maximum value of function f(x) = x^3 occurs at x = 2 and value is 8
and minimum value of function f(x) = x^3 occurs at x = -2 and value is -8

Question:5(ii) Find the absolute maximum value and the absolute minimum value of the following
functions in the given intervals:

f (x) = \sin x + \cos x , x \epsilon [0, \pi]

Answer:

Given function is
f(x) = \sin x + \cos x
f^{'}(x) = \cos x - \sin x\\ f^{'}(x)= 0\\ \cos x- \sin x= 0\\ \cos = \sin x\\ x = \frac{\pi}{4} as x \ \epsilon \ [0,\pi]
Hence, x = \frac{\pi}{4} is the critical point of the function f(x) = \sin x + \cos x
Now, we need to check the value of function f(x) = \sin x + \cos x at x = \frac{\pi}{4} and at the end points of given range i.e. x = 0 \ and \ x = \pi
f(\frac{\pi}{4}) = \sin \frac{\pi}{4} + \cos \frac{\pi}{4}\\
=\frac{1}{\sqrt2}+\frac{1}{\sqrt2} = \frac{2}{\sqrt2} = \sqrt2
f(0) = \sin 0 + \cos 0 = 0 + 1 = 1
f(\pi) = \sin \pi + \cos \pi = 0 +(-1) = -1
Hence, the absolute maximum value of function f(x) = \sin x + \cos x occurs at x = \frac{\pi}{4} and value is \sqrt2
and absolute minimum value of function f(x) = \sin x + \cos x occurs at x = \pi and value is -1

Question:5(iii) Find the absolute maximum value and the absolute minimum value of the following
functions in the given intervals:
f (x) = 4 x - \frac{1}{2} x^2 , x \epsilon \left [ -2 , \frac{9}{2} \right ]

Answer:

Given function is
f(x) =4x - \frac{1}{2}x^2
f^{'}(x) = 4 - x \\ f^{'}(x)= 0\\ 4-x= 0\\ x=4
Hence, x = 4 is the critical point of function f(x) =4x - \frac{1}{2}x^2
Now, we need to check the value of function f(x) =4x - \frac{1}{2}x^2 at x = 4 and at the end points of given range i.e. at x = -2 and x = 9/2
f(4) =4(4) - \frac{1}{2}(4)^2
=16-\frac{1}{2}.16 = 16-8 = 8
f(-2) = 4(-2)-\frac{1}{2}.(-2)^2 = -8-2 = -10
f(\frac{9}{2}) =4(\frac{9}{2})-\frac{1}{2}.\left ( \frac{9}{2} \right )^2 = 18-\frac{81}{8} = \frac{63}{8}
Hence, absolute maximum value of function f(x) =4x - \frac{1}{2}x^2 occures at x = 4 and value is 8
and absolute minimum value of function f(x) =4x - \frac{1}{2}x^2 occures at x = -2 and value is -10

Question:5(iv) Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:

f (x) = ( x-1) ^2 + 3 , x \epsilon [ -3 , 1 ]

Answer:

Given function is
f(x) = (x-1)^2+3
f^{'}(x) =2(x-1) \\ f^{'}(x)= 0\\ 2(x-1)= 0\\ x=1
Hence, x = 1 is the critical point of function f(x) = (x-1)^2+3
Now, we need to check the value of function f(x) = (x-1)^2+3 at x = 1 and at the end points of given range i.e. at x = -3 and x = 1
f(1) = (1-1)^2+3 = 0^2+3 = 3

f(-3) = (-3-1)^2+3= (-4)^2+3 = 16+3= 19
f(1) = (1-1)^2+3 = 0^2+3 = 3
Hence, absolute maximum value of function f(x) = (x-1)^2+3 occurs at x = -3 and value is 19
and absolute minimum value of function f(x) = (x-1)^2+3 occurs at x = 1 and value is 3

Question:6 . Find the maximum profit that a company can make, if the profit function is
given by p(x) = 41 - 72x - 18x ^2

Answer:

Profit of the company is given by the function
p(x) = 41 - 72x - 18x ^2
p^{'}(x)= -72-36x\\ p^{'}(x) = 0\\ -72-36x= 0\\ x = -2
x = -2 is the only critical point of the function p(x) = 41 - 72x - 18x ^2
Now, by second derivative test
p^{''}(x)= -36< 0
At x = -2 p^{''}(x)< 0
Hence, maxima of function p(x) = 41 - 72x - 18x ^2 occurs at x = -2 and maximum value is
p(-2) = 41 - 72(-2) - 18(-2) ^2=41+144-72 = 113
Hence, the maximum profit the company can make is 113 units

Question:7 . Find both the maximum value and the minimum value of
3x^4 - 8x^3 + 12x^2 - 48x + 25 on the interval [0, 3].

Answer:

Given function is
f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}
f^{'}(x)=12x^3 - 24x^2 +24x - 48 \\ f^{'}(x)=0\\ 12(x^3-2x^2+2x-4) = 0\\ x^3-2x^2+2x-4=0\\
Now, by hit and trial let first assume x = 2
(2)^3-2(2)^2+2(2)-4\\ 8-8+4-4=0
Hence, x = 2 is one value
Now,
\frac{x^3-2x^2+2x-4}{x-2} = \frac{(x^2+2)(x-2)}{(x-2)} = (x^2+2)
x^2 = - 2 which is not possible
Hence, x = 2 is the only critical value of function f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{}
Now, we need to check the value at x = 2 and at the end points of given range i.e. x = 0 and x = 3
1628071745575 =3\times16 - 8\times 8 + 12\times 4 - 96 + 25 = 48-64+48-96+25 = -39

f(3)=3(3)^4 - 8(3)^3 + 12(3)^2 - 48(3) + 25\\ =3\times81-8\times27+12\times9-144+25 \\ =243-216+108-144+25 = 16

f(0)=3(0)^4 - 8(0)^3 + 12(0)^2 - 48(0) + 25 = 25
Hence, maximum value of function f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{} occurs at x = 0 and vale is 25
and minimum value of function f(x)=3x^4 - 8x^3 + 12x^2 - 48x + 25^{} occurs at x = 2 and value is -39

Question:8 . At what points in the interval [ 0 , 2 \pi ] does the function \sin 2x attain its maximum value?

Answer:

Given function is
f(x) = \sin 2x
f^{'}(x) = 2\cos 2x\\ f^{'}(x) = 0\\ 2\cos 2x = 0\\ as \ x \ \epsilon [0,2\pi]\\ 0 < x < 2\pi\\ 0< 2x < 4\pi\\ \cos 2x = 0 \ at \ 2x = \frac{\pi}{2},2x = \frac{3\pi}{2},2x=\frac{5\pi}{2}and 2x= \frac{7\pi}{2}\\
So, values of x are
x = \frac{\pi}{4},x = \frac{3\pi}{4},x=\frac{5\pi}{4} \ and \ x= \frac{7\pi}{4}\\ These are the critical points of the function f(x) = \sin 2x
Now, we need to find the value of the function f(x) = \sin 2x at x = \frac{\pi}{4},x = \frac{3\pi}{4},x=\frac{5\pi}{4} \ and \ x= \frac{7\pi}{4}\\ and at the end points of given range i.e. at x = 0 and x = \pi

f(x) = \sin 2x\\ f(\frac{\pi}{4}) = \sin 2\left ( \frac{\pi}{4} \right ) = \sin \frac{\pi}{2} = 1

f(x) = \sin 2x\\ f(\frac{3\pi}{4}) = \sin 2\left ( \frac{3\pi}{4} \right ) = \sin \frac{3\pi}{2} = -1

f(x) = \sin 2x\\ f(\frac{5\pi}{4}) = \sin 2\left ( \frac{5\pi}{4} \right ) = \sin \frac{5\pi}{2} = 1

f(x) = \sin 2x\\ f(\frac{7\pi}{4}) = \sin 2\left ( \frac{7\pi}{4} \right ) = \sin \frac{7\pi}{2} = -1

f(x) = \sin 2x\\ f(\pi) = \sin 2(\pi)= \sin 2\pi = 0

f(x) = \sin 2x\\ f(0) = \sin 2(0)= \sin 0 = 0

Hence, at x =\frac{\pi}{4} \ and \ x = \frac{5\pi}{4} function f(x) = \sin 2x attains its maximum value i.e. in 1 in the given range of x \ \epsilon \ [0,2\pi]

Question:9 What is the maximum value of the function \sin x + \cos x ?

Answer:

Given function is
f(x) = \sin x + \cos x
f^{'}(x) = \cos x - \sin x\\ f^{'}(x)= 0\\ \cos x- \sin x= 0\\ \cos = \sin x\\ x = 2n\pi+\frac{\pi}{4} \ where \ n \ \epsilon \ I
Hence, x = 2n\pi+\frac{\pi}{4} is the critical point of the function f(x) = \sin x + \cos x
Now, we need to check the value of the function f(x) = \sin x + \cos x at x = 2n\pi+\frac{\pi}{4}
Value is same for all cases so let assume that n = 0
Now
f(\frac{\pi}{4}) = \sin \frac{\pi}{4} + \cos \frac{\pi}{4}\\
=\frac{1}{\sqrt2}+\frac{1}{\sqrt2} = \frac{2}{\sqrt2} = \sqrt2

Hence, the maximum value of the function f(x) = \sin x + \cos x is \sqrt2

Question:10. Find the maximum value of 2 x^3 - 24 x + 107 in the interval [1, 3]. Find the
the maximum value of the same function in [–3, –1].

Answer:

Given function is
f(x) = 2x^3-24x+107
f^{'}(x)=6x^2 - 24 \\ f^{'}(x)=0\\ 6(x^2-4) = 0\\ x^2-4=0\\ x^{2} = 4\\ x = \pm2

we neglect the value x =- 2 because x \ \epsilon \ [1,3]
Hence, x = 2 is the only critical value of function f(x) = 2x^3-24x+107
Now, we need to check the value at x = 2 and at the end points of given range i.e. x = 1 and x = 3
f(2) = 2(2)^3-24(2)+107\\ = 2\times 8 - 48+107\\ =16-48+107 = 75

f(3) = 2(3)^3-24(3)+107\\ = 2\times 27 - 72+107\\ =54-72+107 = 89

f(1) = 2(1)^3-24(1)+107\\ = 2\times 1 - 24+107\\ =2-24+107 = 85
Hence, maximum value of function f(x) = 2x^3-24x+107 occurs at x = 3 and vale is 89 when x \ \epsilon \ [1,3]
Now, when x \ \epsilon \ [-3,-1]
we neglect the value x = 2
Hence, x = -2 is the only critical value of function f(x) = 2x^3-24x+107
Now, we need to check the value at x = -2 and at the end points of given range i.e. x = -1 and x = -3
f(-1) = 2(-1)^3-24(-1)+107\\ = 2\times (-1) + 24+107\\ =-2+24+107 = 129

f(-2) = 2(-2)^3-24(-2)+107\\ = 2\times (-8) + 48+107\\ =-16+48+107 = 139

f(-3) = 2(-3)^3-24(-3)+107\\ = 2\times (-27) + 72+107\\ =-54+72+107 = 125
Hence, the maximum value of function f(x) = 2x^3-24x+107 occurs at x = -2 and vale is 139 when x \ \epsilon \ [-3,-1]

Question:11. It is given that at x = 1, the function x ^4 - 62x^2 + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.

Answer:

Given function is
f(x) =x ^4 - 62x^2 + ax + 9
Function f(x) =x ^4 - 62x^2 + ax + 9 attains maximum value at x = 1 then x must one of the critical point of the given function that means
f^{'}(1)=0
f^{'}(x) = 4x^3-124x+a\\ f^{'}(1) = 4(1)^3-124(1)+a\\ f^{'}(1)=4-124+a = a - 120\\
Now,
f^{'}(1)=0\\ a - 120=0\\ a=120
Hence, the value of a is 120

Question:12 . Find the maximum and minimum values of x + \sin 2x \: \:on \: \: [ 0 , 2 \pi ]

Answer:

Given function is
f(x) =x+ \sin 2x
f^{'}(x) =1+ 2\cos 2x\\ f^{'}(x) = 0\\ 1+2\cos 2x = 0\\ as \ x \ \epsilon \ [0,2\pi]\\ 0 < x < 2\pi\\ 0< 2x < 4\pi\\ \cos 2x = \frac{-1}{2} \ at \ 2x = 2n\pi \pm \frac{2\pi}{3} \ where \ n \ \epsilon \ Z\\ x = n\pi \pm \frac{\pi}{3}\\ x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3} \ as \ x \ \epsilon \ [0,2\pi]
So, values of x are
x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3} These are the critical points of the function f(x) = x+\sin 2x
Now, we need to find the value of the function f(x) = x+\sin 2x at x = \frac{\pi}{3},\frac{2\pi}{3},\frac{4\pi}{3},\frac{5\pi}{3} and at the end points of given range i.e. at x = 0 and x = 2\pi

f(x) =x+ \sin 2x\\ f(\frac{\pi}{3}) = \frac{\pi}{3}+\sin 2\left ( \frac{\pi}{3} \right ) = \frac{\pi}{3}+\sin \frac{2\pi}{3} = \frac{\pi}{3}+\frac{\sqrt3}{2}

f(x) =x+ \sin 2x\\ f(\frac{2\pi}{3}) = \frac{2\pi}{3}+\sin 2\left ( \frac{2\pi}{3} \right ) = \frac{2\pi}{3}+\sin \frac{4\pi}{3} = \frac{2\pi}{3}-\frac{\sqrt3}{2}

f(x) =x+ \sin 2x\\ f(\frac{4\pi}{3}) = \frac{4\pi}{3}+\sin 2\left ( \frac{4\pi}{3} \right ) = \frac{4\pi}{3}+\sin \frac{8\pi}{3} = \frac{4\pi}{3}+\frac{\sqrt3}{2}

f(x) =x+ \sin 2x\\ f(\frac{5\pi}{3}) = \frac{5\pi}{3}+\sin 2\left ( \frac{5\pi}{3} \right ) = \frac{5\pi}{3}+\sin \frac{10\pi}{3} = \frac{5\pi}{3}-\frac{\sqrt3}{2}

f(x) = x+\sin 2x\\ f(2\pi) = 2\pi+\sin 2(2\pi)= 2\pi+\sin 4\pi = 2\pi

f(x) = x+\sin 2x\\ f(0) = 0+\sin 2(0)= 0+\sin 0 = 0

Hence, at x = 2\pi function f(x) = x+\sin 2x attains its maximum value and value is 2\pi in the given range of x \ \epsilon \ [0,2\pi]
and at x= 0 function f(x) = x+\sin 2x attains its minimum value and value is 0

Question:13 . Find two numbers whose sum is 24 and whose product is as large as possible.

Answer:

Let x and y are two numbers
It is given that
x + y = 24 , y = 24 - x
and product of xy is maximum
let f(x) = xy=x(24-x)=24x-x^2\\ f^{'}(x) = 24-2x\\ f^{'}(x)=0\\ 24-2x=0\\ x=12
Hence, x = 12 is the only critical value
Now,
f^{''}(x) = -2< 0
at x= 12 f^{''}(x) < 0
Hence, x = 12 is the point of maxima
Noe, y = 24 - x
= 24 - 12 = 12
Hence, the value of x and y are 12 and 12 respectively

Question:14 Find two positive numbers x and y such that x + y = 60 and xy^3 is maximum.

Answer:

It is given that
x + y = 60 , x = 60 -y
and xy^3 is maximum
let f(y) = (60-y)y^3 = 60y^3-y^4
Now,
f^{'}(y) = 180y^2-4y^3\\ f^{'}(y) = 0\\ y^2(180-4y)=0\\ y= 0 \ and \ y = 45

Now,
f^{''}(y) = 360y-12y^2\\ f^{''}(0) = 0\\
hence, 0 is neither point of minima or maxima
f^{''}(y) = 360y-12y^2\\ f^{''}(45) = 360(45)-12(45)^2 = -8100 < 0
Hence, y = 45 is point of maxima
x = 60 - y
= 60 - 45 = 15
Hence, values of x and y are 15 and 45 respectively

Question:15 Find two positive numbers x and y such that their sum is 35 and the product x^2 y^5 is a maximum.

Answer:

It is given that
x + y = 35 , x = 35 - y
and x^2 y^5 is maximum
Therefore,
let \ f (y )= (35-y)^2y^5\\ = (1225-70y+y^2)y^5\\ f(y)=1225y^5-70y^6+y^7
Now,
f^{'}(y) = 6125y^4-420y^5+7y^6\\ f^{'}(y)=0\\ y^4(6125-420y+7y^2) = 0 \\y =0 \ and \ (y-25)(y-35)\Rightarrow y = 25 , y=35
Now,
f^{''}(y)= 24500y^3-2100y^4+42y^5

f^{''}(35)= 24500(35)^3-2100(35)^4+42(35)^5\\ = 105043750 > 0
Hence, y = 35 is the point of minima

f^{''}(0)= 0\\
Hence, y= 0 is neither point of maxima or minima

f^{''}(25)= 24500(25)^3-2100(25)^4+42(25)^5\\ = -27343750 < 0
Hence, y = 25 is the point of maxima
x = 35 - y
= 35 - 25 = 10
Hence, the value of x and y are 10 and 25 respectively

Question:16 . Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.

Answer:

let x an d y are positive two numbers
It is given that
x + y = 16 , y = 16 - x
and x^3 + y^3 is minimum
f(x) = x^3 + (16-x)^3
Now,
f^{'}(x) = 3x^2 + 3(16-x)^2(-1)
f^{'}(x) = 0\\ 3x^2 - 3(16-x)^2 =0\\ 3x^2-3(256+x^2-32x) = 0\\ 3x^2 -3x^2+96x-768= 0\\ 96x = 768\\ x = 8\\
Hence, x = 8 is the only critical point
Now,
f^{''}(x) = 6x - 6(16-x)(-1) = 6x + 96 - 6x = 96\\ f^{''}(x) = 96
f^{''}(8) = 96 > 0
Hence, x = 8 is the point of minima
y = 16 - x
= 16 - 8 = 8
Hence, values of x and y are 8 and 8 respectively

Question:17 . A square piece of tin of side 18 cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.

Answer:

It is given that the side of the square is 18 cm
Let assume that the length of the side of the square to be cut off is x cm
So, by this, we can say that the breath of cube is (18-2x) cm and height is x cm
Then,
Volume of cube \left ( V(x) \right ) = x(18-2x)^2
V^{'}(x) = (18-2x)^2+(x)2(18-2x)(-2)
V^{'}(x) = 0\\ (18-2x)^2-4x(18-2x)=0\\ 324 + 4x^2 - 72x - 72x + 8x^2 = 0\\ 12x^2-144x+324 = 0\\ 12(x^2-12x+27) = 0\\ x^2-9x-3x+27=0\\ (x-3)(x-9)=0\\ x = 3 \ and \ x = 9

But the value of x can not be 9 because then the value of breath become 0 so we neglect value x = 9
Hence, x = 3 is the critical point
Now,
V^{''}(x) = 24x -144\\ V^{''}(3) = 24\times 3 - 144\\ . \ \ \ \ \ \ \ = 72 - 144 = -72\\ V^{''}(3) < 0
Hence, x = 3 is the point of maxima
Hence, the length of the side of the square to be cut off is 3 cm so that the volume of the box is the maximum possible

Question:18 A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum ?

Answer:

It is given that the sides of the rectangle are 45 cm and 24 cm
Let assume the side of the square to be cut off is x cm
Then,
Volume of cube V(x) = x(45-2x)(24-2x)
V^{'}(x) = (45-2x)(24-2x) + (-2)(x)(24-2x)+(-2)(x)(45-2x)\\
1080 + 4x^2 - 138x - 48x + 4x^2 - 90x +4x^2\\ 12x^2 - 276x + 1080
V^{'}(x) = 0\\ 12(x^2 - 23x+90)=0\\ x^2-23x+90 = 0\\ x^2-18x-5x+23=0\\ (x-18)(x-5)=0\\ x =18 \ and \ x = 5
But x cannot be equal to 18 because then side (24 - 2x) become negative which is not possible so we neglect value x= 18
Hence, x = 5 is the critical value
Now,
V^{''}(x)=24x-276\\ V^{''}(5)=24\times5 - 276\\ V^{''}(5)= -156 < 0
Hence, x = 5 is the point of maxima
Hence, the side of the square to be cut off is 5 cm so that the volume of the box is maximum

Question:19 Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.

Answer:

Let assume that length and breadth of rectangle inscribed in a circle is l and b respectively
and the radius of the circle is r
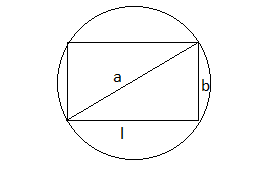
1628071829107 Now, by Pythagoras theorem
a = \sqrt{l^2+b^2}\\
a = 2r
4r^2 = l^2+b^2\\ l = \sqrt{4r^2 - b^2}
Now, area of reactangle(A) = l \times b
A(b) = b(\sqrt{4r^2-b^2})
A^{'}(b) = \sqrt{4r^2-b^2}+b.\frac{(-2b)}{2\sqrt{4r^2-b^2}}\\ = \frac{4r^2-b^2-b^2}{\sqrt{4r^2-b^2}} = \frac{4r^2-2b^2}{\sqrt{4r^2-b^2}}
A^{'}(b) = 0 \\ \frac{4r^2-2b^2}{\sqrt{4r^2-b^2}} = 0\\ 4r^2 = 2b^2\\ b = \sqrt2r
Now,
A^{''}(b) = \frac{-4b(\sqrt{4r^2-b^2})-(4r^2-2b^2).\left ( \frac{-1}{2(4r^2-b^2)^\frac{3}{2}}.(-2b) \right )}{(\sqrt{4r^2-b^2})^2}\\ A^{''}(\sqrt2r) = \frac{(-4b)\times\sqrt2r}{(\sqrt2r)^2} = \frac{-2\sqrt2b}{r}< 0
Hence, b = \sqrt2r is the point of maxima
l = \sqrt{4r^2-b^2}=\sqrt{4r^2-2r^2}= \sqrt2r
Since, l = b we can say that the given rectangle is a square
Hence, of all the rectangles inscribed in a given fixed circle, the square has the maximum area

Question:20 . Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.

Answer:

Let r be the radius of the base of cylinder and h be the height of the cylinder
we know that the surface area of the cylinder (A) = 2\pi r(r+h)
h = \frac{A-2\pi r^2}{2\pi r}
Volume of cylinder
(V) = \pi r^2 h\\ = \pi r^2 \left ( \frac{A-2\pi r^2}{2\pi r} \right ) = r \left ( \frac{A-2\pi r^2}{2 } \right )
V^{'}(r)= \left ( \frac{A-2\pi r^2}{2} \right )+(r).(-2\pi r)\\ = \frac{A-2\pi r^2 -4\pi r^2}{2} = \frac{A-6\pi r^2}{2}
V^{'}(r)= 0 \\ \frac{A-6\pi r^2}{2} = 0\\ r = \sqrt{\frac{A}{6\pi}}
Hence, r = \sqrt{\frac{A}{6\pi}} is the critical point
Now,
V^{''}(r) = -6\pi r\\ V^{''}(\sqrt{\frac{A}{6\pi}}) = - 6\pi . \sqrt{\frac{A}{6\pi}} = - \sqrt{A6\pi} < 0
Hence, r = \sqrt{\frac{A}{6\pi}} is the point of maxima
h = \frac{A-2\pi r^2}{2\pi r} = \frac{2-2\pi \frac{A}{6\pi}}{2\pi \sqrt \frac{A} {6\pi}} = \frac{4\pi \frac{A}{6\pi}}{2\pi \sqrt \frac{A} {6\pi}} = 2\pi \sqrt \frac{A} {6\pi} = 2r
Hence, the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter(D = 2r) of the base

Question:21 Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?

Answer:

Let r be the radius of base and h be the height of the cylinder
The volume of the cube (V) = \pi r^2 h
It is given that the volume of cylinder = 100 cm^3
\pi r^2 h = 100\Rightarrow h = \frac{100}{\pi r^2}
Surface area of cube(A) = 2\pi r(r+h)
A(r)= 2\pi r(r+\frac{100}{\pi r^2})
= 2\pi r ( \frac{\pi r^3+100}{\pi r^2}) = \frac{2\pi r^3+200}{ r} = 2\pi r^2+\frac{200}{r}
A^{'}(r) = 4\pi r + \frac{(-200)}{r^2} \\ A^{'}(r)= 0\\ 4\pi r^3 = 200\\ r^3 = \frac{50}{\pi}\\ r = \left ( \frac{50}{\pi} \right )^{\frac{1}{3}}
Hence, r = (\frac{50}{\pi})^\frac{1}{3} is the critical point
A^{''}(r) = 4\pi + \frac{400r}{r^3}\\ A^{''}\left ( (\frac{50}{\pi})^\frac{1}{3} \right )= 4\pi + \frac{400}{\left ( (\frac{50}{\pi})^\frac{1}{3} \right )^2} > 0
Hence, r = (\frac{50}{\pi})^\frac{1}{3} is the point of minima
h = \frac{100}{\pi r^2} = \frac{100}{\pi \left ( (\frac{50}{\pi})^\frac{1}{3} \right )^2} = 2.(\frac{50}{\pi})^\frac{1}{3}
Hence, r = (\frac{50}{\pi})^\frac{1}{3} and h = 2.(\frac{50}{\pi})^\frac{1}{3} are the dimensions of the can which has the minimum surface area

Question:22 A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?

Answer:

Area of the square (A) = a^2
Area of the circle(S) = \pi r^2
Given the length of wire = 28 m
Let the length of one of the piece is x m
Then the length of the other piece is (28 - x) m
Now,
4a = x\Rightarrow a = \frac{x}{4}
and
2 \pi r = (28-x) \Rightarrow r= \frac{28-x}{2\pi}
Area of the combined circle and square f(x) = A + S
=a^2 + \pi r^2 = (\frac{x}{4})^2+\pi (\frac{28-x}{2\pi})^2
f^{'}(x) = \frac{2x}{16}+\frac{(28-x)(-1)}{2\pi} \\ f^{'}(x) = \frac{x\pi+4x-112}{8\pi}\\ f^{'}(x) = 0\\ \frac{x\pi+4x-112}{8\pi} = 0\\ x(\pi+4) = 112\\ x = \frac{112}{\pi + 4}
Now,
f^{''}(x) = \frac{1}{8}+ \frac{1}{2\pi}\\ f^{''}(\frac{112}{\pi+4}) = \frac{1}{8}+ \frac{1}{2\pi} > 0
Hence, x = \frac{112}{\pi+4} is the point of minima
Other length is = 28 - x
= 28 - \frac{112}{\pi+4} = \frac{28\pi+112-112}{\pi+4} = \frac{28\pi}{\pi+4}
Hence, two lengths are \frac{28\pi}{\pi+4} and \frac{112}{\pi+4}

Question:23 Prove that the volume of the largest cone that can be inscribed in a sphere of radius r is 8/27 of the volume of the sphere.

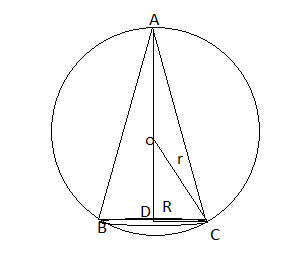
Answer: 1654609173546 Volume of cone (V) = \frac{1}{3}\pi R^2h
Volume of sphere with radius r = \frac{4}{3}\pi r^3
By pythagoras theorem in \Delta ADC we ca say that
OD^2 = r^2 - R^2 \\ OD = \sqrt{r^2 - R^2}\\ h = AD = r + OD = r + \sqrt{r^2 - R^2}
V = \frac{1}{3}\pi R^2 (r + \sqrt{r^2+R^2})\\ = \frac{1}{3}\pi R^2r + \frac{1}{3}\pi R^2 \sqrt{r^2+R^2}
\frac{1}{3}\pi R^2 (r + \sqrt{r^2-R^2})\\ V^{'}(R)= \frac{2}{3}\pi Rr + \frac{2}{3}\pi R \sqrt{r^2-R^2}+\frac{1}{3}\pi R^2.\frac{-2R}{2\sqrt{r^2-R^2}}\\ V^{'}(R) = 0\\ \frac{1}{3}\pi R \left ( 2r + 2\sqrt{r^2-R^2} - \frac{R^2}{\sqrt{r^2-R^2}} \right ) = 0\\ \frac{1}{3}\pi R \left ( \frac{2r\sqrt{r^2-R^2} + 2r^2-2R^2 -R^2}{\sqrt{r^2-R^2}} \right ) = 0\\ R \neq 0 \ So, \\ 2r\sqrt{r^2-R^2} = 3R^2 - 2r^2\\ Square \ both \ sides\\ 4r^4-4r^2R^2 = 9R^4 + 4r^4 - 12R^2r^2\\ 9R^4-8R^2r^2 = 0\\ R^2(9R^2-8r^2) = 0\\ R \neq 0 \ So, 9R^2 = 8r^2\\ R = \frac{2\sqrt2r}{3}
Now,
V^{''}(R)= \frac{2}{3}\pi r + \frac{2}{3}\pi \sqrt{r^2-R^2}+\frac{2}{3}\pi R.\frac{-2R}{2\sqrt{r^2-R^2}}-\frac{3\pi R^2}{\sqrt{r^2-R^2}} - \frac{(-1)(-2R)}{(r^2+R^2)\frac{3}{2}}\\ V^{''}(\frac{2\sqrt2r}{3}) < 0
Hence, point R = \frac{2\sqrt2r}{3} is the point of maxima
h = r + \sqrt{r^2-R^2} = r + \sqrt{r^2-\frac{8r^2}{9}} = r + \frac{r}{3} = \frac{4r}{3}
Hence, the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is \frac{4r}{3}
Volume = = \frac{1}{3}\pi R^2h = \frac{1}{3}\pi \frac{8r^2}{9}.\frac{4r}{3} = \frac{8}{27}.\frac{4}{3}\pi r^3 = \frac{8}{27}\times \ volume \ of \ sphere
Hence proved

Question:24 Show that the right circular cone of least curved surface and given volume has an altitude equal to \sqrt 2 time the radius of the base.

Answer:

Volume of cone(V)

\frac{1}{3}\pi r^2h \Rightarrow h = \frac{3V}{\pi r^2}
curved surface area(A) = \pi r l
l^2 = r^2 + h^2\\ l = \sqrt{r^2+\frac{9V^2}{\pi^2r^4}}
A = \pi r \sqrt{r^2+\frac{9V^2}{\pi^2r^4}} = \pi r^2 \sqrt{1+\frac{9V^2}{\pi^2r^6}}

\frac{dA}{dr} = 2\pi r \sqrt{1+\frac{9V^2}{\pi^2r^6}}+ \pi r^2.\frac{1}{2\sqrt{1+\frac{9V^2}{\pi^2r^6}}}.\frac{(-6r^5)9V^2}{\pi^2r^7}\\ \frac{dA}{dr} = 0\\ 2\pi r \sqrt{1+\frac{9V^2}{\pi^2r^6}}+ \pi r^2.\frac{1}{2\sqrt{1+\frac{9V^2}{\pi^2r^6}}}.\frac{(-6)9V^2}{\pi^2r^7} = 0 \\ 2\pi^2r^6\left ( 1+\frac{9V^2}{\pi^2r^6} \right ) = {27V^2}\\ 2\pi^2r^6\left ( \frac{\pi^2r^6+9V^2}{\pi^2r^6} \right ) = {27V^2}\\ 2\pi^2r^6 + 18V^2 = 27V^2\\ 2\pi^2r^6 = 9V^2\\ r^6 = \frac{9V^2}{2\pi^2}
Now , we can clearly varify that
\frac{d^2A}{dr^2} > 0
when r^6 =\frac{9V^2}{2\pi^2}
Hence, r^6 =\frac{9V^2}{2\pi^2} is the point of minima
V = \frac{\sqrt2\pi r^3}{3}
h = \frac{3V}{\pi r^2} = \frac{3.\frac{\sqrt2\pi r^3}{3}}{\pi r^2} = \sqrt2 r
Hence proved that the right circular cone of least curved surface and given volume has an altitude equal to \sqrt 2 time the radius of the base

Question:25 Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is \tan ^{-1} \sqrt 2

Answer:

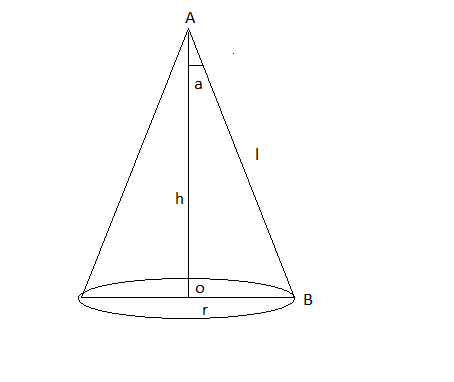
1628071922992 Let a be the semi-vertical angle of cone
Let r , h , l are the radius , height , slent height of cone
Now,
r = l\sin a \ and \ h=l\cos a
we know that
Volume of cone (V) = \frac{1}{3}\pi r^2 h = \frac{1}{3}\pi (l\sin a)^2(l\cos a) = \frac{\pi l^3\sin^2 a\cos a}{3}
Now,
\frac{dV}{da}= \frac{\pi l^3}{3}\left ( 2\sin a\cos a.\cos a+\sin^2a.(-\sin a)\right )= \frac{\pi l^3}{3}\left ( 2\sin a\cos^2a-\sin^3a \right )
\frac{dV}{da}=0\\ \frac{\pi l^3}{3}\left ( 2\sin a\cos^2a-\sin^3a \right ) = 0\\ 2\sin a\cos^2a-\sin^3a= 0\\ 2\sin a\cos^2a=\sin^3a\\ \tan^2 a = 2\\ a = \tan^{-1}\sqrt 2
Now,
\frac{d^2V}{da^2}= \frac{\pi l^3}{3}\left ( 2\cos a\cos^2a+2\cos a(-2\cos a\sin a+3\sin^2a\cos a) \right )
Now, at a= \tan ^{-1}\sqrt 2
\frac{d^2V}{dx^2}< 0
Therefore, a= \tan ^{-1}\sqrt 2 is the point of maxima
Hence proved

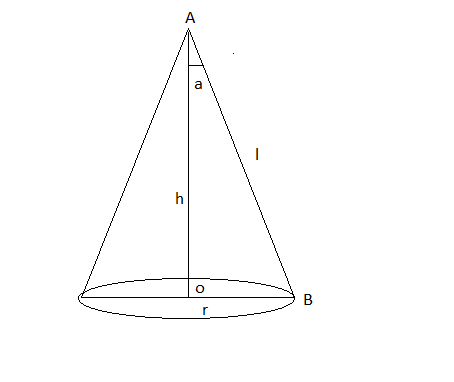
Question:26 Show that semi-vertical angle of the right circular cone of given surface area and maximum volume is \sin ^{-1} (1/3)

Answer:

1628071965473 Let r, l, and h are the radius, slant height and height of cone respectively
Now,
r = l\sin a \ and \ h =l\cos a
Now,
we know that
The surface area of the cone (A) = \pi r (r+l)
A= \pi l\sin a l(\sin a+1)\\ \\ l^2 = \frac{A}{\pi \sin a(\sin a+1)}\\ \\ l = \sqrt{\frac{A}{\pi \sin a(\sin a+1)}}
Now,
Volume of cone(V) =

\frac{1}{3}\pi r^2h = \frac{1}{3}\pi l^3 \sin^2 a\cos a= \frac{\pi}{3}.\left ( \frac{A}{\pi\sin a(\sin a+1)} \right )^\frac{3}{2}.\sin^2 a\cos a
On differentiate it w.r.t to a and after that
\frac{dV}{da}= 0
we will get
a = \sin^{-1}\frac{1}{3}
Now, at a = \sin^{-1}\frac{1}{3}
\frac{d^2V}{da^2}<0
Hence, we can say that a = \sin^{-1}\frac{1}{3} is the point if maxima
Hence proved

Question:27 The point on the curve x^2 = 2y which is nearest to the point (0, 5) is

(A) (2 \sqrt 2,4) \: \: (B) (2 \sqrt 2,0)\: \: (C) (0, 0)\: \: (D) (2, 2)

Answer:

Given curve is
x^2 = 2y
Let the points on curve be \left ( x, \frac{x^2}{2} \right )
Distance between two points is given by
f(x)= \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
= \sqrt{(x-0)^2+(\frac{x^2}{2}-5)^2} = \sqrt{x^2+ \frac{x^4}{4}-5x^2+25} = \sqrt{ \frac{x^4}{4}-4x^2+25}
f^{'}(x) = \frac{x^3-8x}{2\sqrt{\frac{x^4}{4}-4x^2+25}}\\ f^{'}(x)= 0\\ \frac{x^3-8x}{2\sqrt{\frac{x^4}{4}-4x^2+25}} =0\\ x(x^2 - 8)=0\\x=0 \ and \ x^2 = 8\Rightarrow x = 2\sqrt2
f^{''}(x) = \frac{1}{2}\left (\frac{(3x^2-8)(\sqrt{\frac{x^4}{4}-4x^2+25} - (x^3-8x).\frac{(x^3-8x)}{2\sqrt{\frac{x^4}{4}-4x^2+25}}}{(\sqrt{\frac{x^4}{4}-4x^2+25})^2}) \right )
f^{''}(0) = -8 < 0
Hence, x = 0 is the point of maxima
f^{''}(2\sqrt2) > 0
Hence, the point x = 2\sqrt2 is the point of minima
x^2 = 2y\Rightarrow y = \frac{x^2}{2} = \frac{8}{2}=4
Hence, the point (2\sqrt2,4) is the point on the curve x^2 = 2y which is nearest to the point (0, 5)
Hence, the correct answer is (A)

Question:28 For all real values of x, the minimum value of \frac{1- x + x^2 }{1+ x +x^2}
is
(A) 0 (B) 1 (C) 3 (D) 1/3

Answer:

Given function is
f(x)= \frac{1- x + x^2 }{1+ x +x^2}
f^{'}(x)= \frac{(-1+2x)(1+x+x^2)-(1-x+x^2)(1+2x)}{(1+ x +x^2)^2}
= \frac{-1-x-x^2+2x+2x^2+2x^3-1-2x+x+2x^2-x^2-2x^3}{(1+ x +x^2)^2} = \frac{-2+2x^2}{(1+ x +x^2)^2}
f^{'}(x)=0\\ \frac{-2+2x^2}{(1+ x +x^2)^2} = 0\\ x^2 = 1\\ x= \pm 1
Hence, x = 1 and x = -1 are the critical points
Now,
f^{''}(x)= \frac{4x(1+ x +x^2)^2-(-2+2x^2)2(1+x+x^2)(2x+1)}{(1+ x +x^2)^4} \\ f^{''}(1) = \frac{4\times(3)^2}{3^4} = \frac{4}{9} > 0
Hence, x = 1 is the point of minima and the minimum value is
f(1)= \frac{1- 1 + 1^2 }{1+ 1 +1^2} = \frac{1}{3}

f^{''}(-1) =-4 < 0
Hence, x = -1 is the point of maxima
Hence, the minimum value of
\frac{1- x + x^2 }{1+ x +x^2} is \frac{1}{3}
Hence, (D) is the correct answer

Question:29 The maximum value of [ x ( x-1)+ 1 ] ^{1/3 } , 0\leq x \leq 1
(A) \left ( \frac{1}{3} \right ) ^{1/3}\: \: (B) 1 /2\: \: (C) 1\: \: (D) 0

Answer:

Given function is
f(x) = [ x ( x-1)+ 1 ] ^{1/3 }
f^{'}(x) = \frac{1}{3}.[(x-1)+x].\frac{1}{[x(x-1)+1]^\frac{2}{3}} = \frac{2x-1}{3[x(x-1)+1]^\frac{2}{3}}
f^{'}(x) = 0\\ \frac{2x-1}{3[x(x-1)+1]^\frac{2}{3}} = 0\\ x =\frac{1}{2}
Hence, x = 1/2 is the critical point s0 we need to check the value at x = 1/2 and at the end points of given range i.e. at x = 1 and x = 0
f(\frac{1}{2}) = [ \frac{1}{2} ( \frac{1}{2}-1)+ 1 ] ^{1/3 } = \left ( \frac{3}{4} \right )^\frac{1}{3}
f(0) = [ 0 ( 0-1)+ 1 ] ^{1/3 } = \left ( 1 \right )^\frac{1}{3} = 1
f(1) = [ 1 ( 1-1)+ 1 ] ^{1/3 } = \left ( 1 \right )^\frac{1}{3} = 1
Hence, by this we can say that maximum value of given function is 1 at x = 0 and x = 1

option c is correct

More About NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5

  • There are 29 questions in exercise 6.5 Class 12 Maths.
  • Question numbers 27 to 29 of Class 12th Maths chapter 6 exercise 6.5 are multiple-choice questions.
  • There will be 4 choices given for multiple-choice questions in the NCERT and have to select the correct answer.
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Also Read| Application of Derivatives Class 12 Notes

Benefits of NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.5

  • The exercise 6.5 Class 12 Maths is solved by expert Mathematics faculties and students can rely on Class 12th Maths chapter 6 exercise 6.5 for exam preparation.
  • Not only for board exams but also for competitive exams like JEE main the NCERT solutions for Class 12 Maths chapter 6 exercise 6.5 will be helpful.
  • Students can access these solutions for free.
JEE Main Important Mathematics Formulas

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

Apply

Key Features Of NCERT Solutions for Exercise 6.5 Class 12 Maths Chapter 6

  • Comprehensive Coverage: The solutions encompass all the topics covered in ex 6.5 class 12, ensuring a thorough understanding of the concepts.
  • Step-by-Step Solutions: In this class 12 maths ex 6.5, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
  • Accuracy and Clarity: Solutions for class 12 ex 6.5 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
  • Conceptual Clarity: In this 12th class maths exercise 6.5 answers, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
  • Inclusive Approach: Solutions for ex 6.5 class 12 cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
  • Relevance to Curriculum: The solutions for class 12 maths ex 6.5 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Question (FAQs)

1. What are the topics covered in exercise 6.5?

The topic of maxima and minima is covered in Class 12th Maths chapter 6 exercise 6.5.

2. How many examples are solved before Class 12 Maths exercise 6.5 on the topic maxima and minima?

16 questions are explained before exercise 6.5

3. What is the total number of solved examples in the NCERT book till Exercise 6.5 Class 12 Maths?

A sum of 41 questions are solved till the Class 12th Maths chapter 6 exercise 6.5

4. Give some applications of maxima and minima?

The problems of maxima and minima are used in business, science and mathematics etc. Examples are problems related to maximising profit, minimising the distance between the two points etc

5. What is a monotonic function in a given interval?

In the given interval, a monotonic function is either increasing or decreasing. 

6. For a function f, if k is a point of local maxima, then what is the local maximum value of the function is?

The local maximum value is f(k)

7. For a function f, if u is a point of local minima, then what is the local minimum value of the function is?

f(u) is the local minimum value of function f

8. Is the topic maxima and minima important for board exams?

Yes, maxima and minima are one of the important topics of the chapter from where 1 question can be expected for CBSE board exam

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:01 August,2024 - 16 September,2024

National Rural Talent Scholarship Examination

Application Date:05 September,2024 - 20 September,2024

International General Knowledge Olympiad

Exam Date:19 September,2024 - 19 September,2024

Unified Cyber Olympiad

Exam Date:20 September,2024 - 20 September,2024

National Institute of Open Schooling 10th examination

Exam Date:20 September,2024 - 07 October,2024

View All School Exams

Certifications By Top Providers

Edx
 1113 courses
Coursera
 804 courses
Udemy
 394 courses
Futurelearn
 222 courses
Harvard University, Cambridge
 98 courses
IBM
 85 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

You can use them people also used problem

Read Complete Answer
Divyan 06 August,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

The Medhavi National Scholarship Program, under the Human Resources & Development Mission (HRDM), offers financial assistance to meritorious students through a scholarship exam. To be eligible, candidates must be between 16 and 40 years old as of the last date of registration and have at least passed the 10th grade from a recognized board. Higher qualifications, such as 11th/12th grade, graduation, post-graduation, or a diploma, are also acceptable.

To apply, download the Medhavi App from the Google Play Store, sign up, and read the detailed notification about the scholarship exam. Complete the registration within the app, take the exam from home using the app, and receive your results within two days. Following this, upload the necessary documents and bank account details for verification. Upon successful verification, the scholarship amount will be directly transferred to your bank account.

The scholarships are categorized based on the marks obtained in the exam: Type A for those scoring 60% or above, Type B for scores between 50% and 60%, and Type C for scores between 40% and 50%. The cash scholarships range from Rs. 2,000 to Rs. 18,000 per month, depending on the exam and the marks obtained.

Since you already have a 12th-grade qualification with 84%, you meet the eligibility criteria and can apply for the Medhavi Scholarship exam. Preparing well for the exam can increase your chances of receiving a higher scholarship.

Read Complete Answer
Yuvan 01 September,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
I have completed my 12th with arts cbse. I want to repeat my 12th with pcmb. How to become a private candidate and what are deadline to be able to appear in 2025 exam?

Hello student,

If you are planning to appear again for class 12th board exam with PCMB as a private candidate here is the right information you need:

  • No school admission needed! Register directly with CBSE. (But if you want to attend the school then you can take admission in any private school of your choice but it will be waste of money)
  • You have to appear for the 2025 12th board exams.
  • Registration for class 12th board exam starts around September 2024 (check CBSE website for exact dates).
  • Aim to register before late October to avoid extra fees.
  • Schools might not offer classes for private students, so focus on self-study or coaching.

Remember , these are tentative dates based on last year. Keep an eye on the CBSE website ( https://www.cbse.gov.in/ ) for the accurate and official announcement.

I hope this answer helps you. If you have more queries then feel free to share your questions with us, we will be happy to help you.

Good luck with your studies!

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

VMC VIQ Scholarship Test
VMC VIQ Scholarship Test
Apply

Register for Vidyamandir Intellect Quest. Get Scholarship and Cash Rewards.

Tallentex 2025 - ALLEN's Talent Encouragement Exam
Tallentex 2025 - ALLEN's Talent Encouragement Exam
Apply

Register for Tallentex '25 - One of The Biggest Talent Encouragement Exam

JEE Main Important Physics formulas
JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Pearson | PTE
Apply

Register now for PTE & Unlock 10% OFF : Use promo code: 'C360SPL10'. Limited Period Offer! Trusted by 3,500+ universities globally

View All Application Forms
News and Notifications
CBSE sample paper 2024-25, marking scheme out for skill education subjects
September 02, 2024 - 12:13 PM IST
CBSE to overhaul internal assessment system, develop framework with British Council
August 28, 2024 - 04:58 PM IST
65 lakh students didn't clear Class 10, 12 board exams last year: Education ministry
August 21, 2024 - 10:24 PM IST
CBSE Compartment Result 2024: Marks verification, answer book photocopy, revaluation dates out
August 06, 2024 - 12:37 PM IST
CBSE Class 12 compartment results 2024 declared at cbseresults.nic.in; 29.78% pass
August 02, 2024 - 04:46 PM IST
CBSE best, Kerala board worst in curriculum, infrastructure: NCERT PARAKH report
July 30, 2024 - 04:48 PM IST
Assign 40% weightage to Class 12 exam in final result; have ‘on-demand exams’: NCERT PARAKH report
July 29, 2024 - 07:54 PM IST

Stay up-to date with CBSE Class 12th News

Back to top