NCERT Solutions for Exercise 6.2 Class 12 Maths Chapter 10

NCERT Solutions for Exercise 6.2 Class 12 Maths Chapter 10 - Application of Derivatives

Edited By Ramraj Saini | Updated on Dec 03, 2023 08:40 PM IST | #CBSE Class 12th

Upcoming Event

CBSE Class 12th Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 12 Maths Chapter 6 Exercise 6.2

NCERT Solutions for Exercise 6.2 Class 12 Maths Chapter 6 Application of Derivatives are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. NCERT solutions for exercise 6.2 Class 12 Maths chapter 6 gives an insight into topic 6.3 increasing and decreasing functions. Before exercise 6.2 Class 12 Maths, NCERT has explained the questions and examples related to the rate of change of quantities. After the NCERT solutions for Class 12 Maths chapter 6 exercise 6.2 the concepts of decreasing and increasing functions is introduced in the NCERT book and then certain theorems are discussed followed by example questions and Class 12th Maths chapter 6 exercise 6.2.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

The NCERT solutions for Class 12 Maths chapter 6 exercise 6.2 gives practice on topic 6.3 of Class 12 Maths NCERT syllabus. Solving the Class 12 Maths chapter 6 exercise 6.2 gives more knowledge of the concepts of increasing and decreasing functions. The following exercises are also discussed in the chapter application of derivatives. 12th class Maths exercise 6.2 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Assess NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2

Download PDF

Application of Derivatives Class 12 Exercise 6.2

Question:1 . Show that the function given by f (x) = 3x + 17 is increasing on R.

Answer:

Let $x_1 and x_2$ are two numbers in R
$x_1 < x_2 \Rightarrow 3x_1 < 3 x_2 \Rightarrow 3x_1 + 17 < 3x_2+17 \Rightarrow f(x_1)< f(x_2)$
Hence, f is strictly increasing on R

Question:2. Show that the function given by $f(x) = e^{2x}$ is increasing on R.

Answer:

Let $x_1 \ and \ x_2$ are two numbers in R
$x_1 \ < \ x_2 \Rightarrow 2x_1 < 2x_2 \Rightarrow e^{2x_1} < e^{2x_2} \Rightarrow f(x_1) < f(x_2)$
Hence, the function $f(x) = e^{2x}$ is strictly increasing in R

Question:3 a) Show that the function given by f (x) = $\sin x$ is increasing in $\left ( 0 , \pi /2 \right )$

Answer:

Given f(x) = sinx
$f^{'}(x) = \cos x$
Since, $\cos x > 0 \ for \ each \ x\ \epsilon \left ( 0,\frac{\pi}{2} \right )$
$f^{'}(x) > 0$
Hence, f(x) = sinx is strictly increasing in $\left ( 0,\frac{\pi}{2} \right )$

Question:3 b) Show that the function given by f (x) = $\sin x$ is

decreasing in $\left ( \frac{\pi}{2},\pi \right )$

Answer:

f(x) = sin x
$f^{'}(x) = \cos x$
Since, $\cos x < 0$ for each $x \ \epsilon \left ( \frac{\pi}{2},\pi \right )$
So, we have $f^{'}(x) < 0$
Hence, f(x) = sin x is strictly decreasing in $\left ( \frac{\pi}{2},\pi \right )$

Question:3 c) Show that the function given by f (x) = $\sin x$ is neither increasing nor decreasing in $( 0 , \pi )$

Answer:

We know that sin x is strictly increasing in $\left ( 0,\frac{\pi}{2} \right )$ and strictly decreasing in $\left ( \frac{\pi}{2},\pi \right )$
So, by this, we can say that f(x) = sinx is neither increasing or decreasing in range $\left ( 0,\pi \right )$

Question:4(a). Find the intervals in which the function f given by $f ( x) = 2x ^2 - 3 x$ is increasing

Answer:

$f ( x) = 2x ^2 - 3 x$
$f^{'}(x) = 4x - 3$
Now,
$f^{'}(x) = 0$
4x - 3 = 0
$x = \frac{3}{4}$
1628071298489 So, the range is $\left ( -\infty, \frac{3}{4} \right ) \ and \ \left ( \frac{3}{4}, \infty \right )$
So,
$f(x)< 0$ when $x \ \epsilon \left ( -\infty,\frac{3}{4} \right )$ Hence, f(x) is strictly decreasing in this range
and
$f(x) > 0$ when $x \epsilon \left ( \frac{3}{4},\infty \right )$ Hence, f(x) is strictly increasing in this range
Hence, $f ( x) = 2x ^2 - 3 x$ is strictly increasing in $x \epsilon \left ( \frac{3}{4},\infty \right )$

Question:4(b) Find the intervals in which the function f given by $f ( x) = 2 x ^2 - 3 x$ is
decreasing

Answer:

$f ( x) = 2x ^2 - 3 x$
$f^{'}(x) = 4x - 3$
Now,
$f^{'}(x) = 0$
4x - 3 = 0
$x = \frac{3}{4}$
1654596806436 So, the range is $\left ( -\infty, \frac{3}{4} \right ) \ and \ \left ( \frac{3}{4}, \infty \right )$
So,
$f(x)< 0$ when $x \ \epsilon \left ( -\infty,\frac{3}{4} \right )$ Hence, f(x) is strictly decreasing in this range
and
$f(x) > 0$ when $x \epsilon \left ( \frac{3}{4},\infty \right )$ Hence, f(x) is strictly increasing in this range
Hence, $f ( x) = 2x ^2 - 3 x$ is strictly decreasing in $x \epsilon \left ( -\infty ,\frac{3}{4}\right )$

Question:5(a) Find the intervals in which the function f given by $f (x) = 2x^3 - 3x ^2 - 36 x + 7$ is
increasing

Answer:

It is given that
$f (x) = 2x^3 - 3x ^2 - 36 x + 7$
So,
$f^{'}(x)= 6x^{2} - 6x - 36$
$f^{'}(x)= 0$
$6x^{2} - 6x -36 =0 \Rightarrow 6 (x^{2} - x-6)$
$x^{2} - x-6 = 0$
$x^{2} - 3x+2x-6 = 0$
$x(x-3) + 2(x-3) = 0\\$
$(x+2)(x-3) = 0$
x = -2 , x = 3

So, three ranges are there $(-\infty,-2) , (-2,3) \ and \ (3,\infty)$
Function $f^{'}(x)= 6x^{2} - 6x - 36$ is positive in interval $(-\infty,-2) , (3,\infty)$ and negative in the interval (-2,3)
Hence, $f (x) = 2x^3 - 3x ^2 - 36 x + 7$ is strictly increasing in $(-\infty,-2) \cup (3,\infty)$
and strictly decreasing in the interval (-2,3)

Question:5(b) Find the intervals in which the function f given by $f ( x) = 2x ^3 - 3x ^2 - 36x + 7$ is
decreasing

Answer:

We have

Differentiating the function with respect to x, we get :

$f' ( x) = 6x ^2 - 6x - 36$

or $= 6\left ( x-3 \right )\left ( x+2 \right )$

When $f'(x)\ =\ 0$ , we have :

$0\ = 6\left ( x-3 \right )\left ( x+2 \right )$

or $\left ( x-3 \right )\left ( x+2 \right )\ =\ 0$

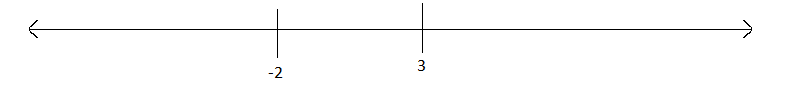
1654597172033 So, three ranges are there $(-\infty,-2) , (-2,3) \ and \ (3,\infty)$
Function $f^{'}(x)= 6x^{2} - 6x - 36$ is positive in the interval $(-\infty,-2) , (3,\infty)$ and negative in the interval (-2,3)

So, f(x) is decreasing in (-2, 3)

Question:6(a) Find the intervals in which the following functions are strictly increasing or
decreasing: $x ^2 + 2x -5$

Answer:

f(x) = $x ^2 + 2x -5$
$f^{'}(x) = 2x + 2 = 2(x+1)$
Now,
$f^{'}(x) = 0 \\ 2(x+1) = 0\\ x = -1$

The range is from $(-\infty,-1) \ and \ (-1,\infty)$
In interval $(-\infty,-1)$ $f^{'}(x)= 2(x+1)$ is -ve
Hence, function f(x) = $x ^2 + 2x -5$ is strictly decreasing in interval $(-\infty,-1)$
In interval $(-1,\infty)$ $f^{'}(x)= 2(x+1)$ is +ve
Hence, function f(x) = $x ^2 + 2x -5$ is strictly increasing in interval $(-1,\infty)$

Question:6(b) Find the intervals in which the following functions are strictly increasing or
decreasing

$10 - 6x - 2x^2$

Answer:

Given function is,
$f(x) = 10 - 6x - 2x^2$
$f^{'}(x) = -6 - 4x$
Now,
$f^{'}(x) = 0$
$6+4x= 0$
$x= -\frac{3}{2}$
So, the range is $(-\infty , -\frac{3}{2}) \ and \ (-\frac{3}{2},\infty)$
In interval $(-\infty , -\frac{3}{2})$ , $f^{'}(x) = -6 - 4x$ is +ve
Hence, $f(x) = 10 - 6x - 2x^2$ is strictly increasing in the interval $(-\infty , -\frac{3}{2})$
In interval $( -\frac{3}{2},\infty)$ , $f^{'}(x) = -6 - 4x$ is -ve
Hence, $f(x) = 10 - 6x - 2x^2$ is strictly decreasing in interval $( -\frac{3}{2},\infty)$

Question:6(c) Find the intervals in which the following functions are strictly increasing or
decreasing:

$- 2 x^3 - 9x ^2 - 12 x + 1$

Answer:

Given function is,
$f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$
$f^{'}(x) = - 6 x^2 - 18x - 12$
Now,
$f^{'}(x) = 0\\ - 6 x^2 - 18x - 12 = 0\\ -6(x^{2}+3x+2) = 0 \\ x^{2}+3x+2 = 0 \\x^{2} + x + 2x + 2 = 0\\ x(x+1) + 2(x+1) = 0\\ (x+2)(x+1) = 0\\ x = -2 \ and \ x = -1$

So, the range is $(-\infty , -2) \ , (-2,-1) \ and \ (-1,\infty)$
In interval $(-\infty , -2) \cup \ (-1,\infty)$ , $f^{'}(x) = - 6 x^2 - 18x - 12$ is -ve
Hence, $f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$ is strictly decreasing in interval $(-\infty , -2) \cup \ (-1,\infty)$
In interval (-2,-1) , $f^{'}(x) = - 6 x^2 - 18x - 12$ is +ve
Hence, $f(x) = - 2 x^3 - 9x ^2 - 12 x + 1^{}$ is strictly increasing in the interval (-2,-1)

Question:6(d) Find the intervals in which the following functions are strictly increasing or
decreasing:

$6- 9x - x ^2$

Answer:

Given function is,
$f(x) = 6- 9x - x ^2$
$f^{'}(x) = - 9 - 2x$
Now,
$f^{'}(x) = 0\\ - 9 - 2x = 0 \\ 2x = -9\\ x = -\frac{9}{2}$

So, the range is $(-\infty, - \frac{9}{2} ) \ and \ ( - \frac{9}{2}, \infty )$
In interval $(-\infty, - \frac{9}{2} )$ , $f^{'}(x) = - 9 - 2x$ is +ve
Hence, $f(x) = 6- 9x - x ^2$ is strictly increasing in interval $(-\infty, - \frac{9}{2} )$
In interval $( - \frac{9}{2},\infty )$ , $f^{'}(x) = - 9 - 2x$ is -ve
Hence, $f(x) = 6- 9x - x ^2$ is strictly decreasing in interval $( - \frac{9}{2},\infty )$

Question:6(e) Find the intervals in which the following functions are strictly increasing or
decreasing:

$( x+1) ^3 ( x-3) ^3$

Answer:

Given function is,
$f(x) = ( x+1) ^3 ( x-3) ^3$
$f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$
Now,
$f^{'}(x) = 0 \\ 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^{3} \\ 3(x+1)^{2}(x-3)^{2}((x-3) + (x+1) ) = 0 \\ (x+1)(x-3) = 0 \ \ \ \ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ (2x-2) = 0\\ x=-1 \ and \ x = 3 \ \ \ \ \ \ \ \ \ \ \ \ \ \ or \ \ \ \ \ \ \ \ \ \ \ \ x = 1$
So, the intervals are $(-\infty,-1), (-1,1), (1,3) \ and \ (3,\infty)$

Our function $f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$ is +ve in the interval $(1,3) \ and \ (3,\infty)$
Hence, $f(x) = ( x+1) ^3 ( x-3) ^3$ is strictly increasing in the interval $(1,3) \ and \ (3,\infty)$
Our function $f^{'}(x) = 3( x+1) ^2(x-3)^{3} + 3( x-3) ^2(x+1)^3$ is -ve in the interval $(-\infty,-1) \ and \ (-1,1)$
Hence, $f(x) = ( x+1) ^3 ( x-3) ^3$ is strictly decreasing in interval $(-\infty,-1) \ and \ (-1,1)$

Question:7 Show that $y = \log( 1+ x ) - \frac{2 x }{2+x } , x > -1$ is an increasing function of x throughout its domain.

Answer:

Given function is,
$f(x)\Rightarrow y = \log( 1+ x ) - \frac{2 x }{2+x }$
$f^{'}(x)\Rightarrow \frac{dy}{dx} = \frac{1}{1+x} - \frac{2 (2+x) - (1)(2x)} {(2+x)^{2} } = \frac{1}{1+x} - \frac{4+2x-2x}{(2+x)^{2}}$
$= \frac{1}{1+x} - \frac{4}{(2+x)^2} = \frac{(2+x)^2 - 4(x+1)}{(x+1)(2+x)^{2}}$
$= \frac{4+x^{2} +4x -4x - 4}{(x+1)(2+x)^{2}} = \frac{x^{2} }{(x+1)(2+x)^{2}}$
$f^{'}(x) = \frac{x^{2}}{(x+1)(x+2)^2}$
Now, for $x > -1$ , is is clear that $f^{'}(x) = \frac{x^{2}}{(x+1)(x+2)^2} > 0$
Hence, $f(x)\Rightarrow y = \log( 1+ x ) - \frac{2 x }{2+x }$ strictly increasing when $x > -1$

Question:8 Find the values of x for which $y = [x(x-2)]^{2}$ is an increasing function.

Answer:

Given function is,
$f(x)\Rightarrow y = [x(x-2)]^{2}$
$f^{'}(x)\Rightarrow \frac{dy}{dx} = 2[x(x-2)][(x-2)+x]$
$= 2(x^2-2x)(2x-2)$
$= 4x(x-2)(x-1)$
Now,
$f^{'}(x) = 0\\ 4x(x-2)(x-1) = 0\\ x=0 , x= 2 \ and \ x = 1$
So, the intervals are $(-\infty,0),(0,1),(1,2) \ and \ (2,\infty)$
In interval $(0,1)and \ (2,\infty)$ , $f^{'}(x)> 0$
Hence, $f(x)\Rightarrow y = [x(x-2)]^{2}$ is an increasing function in the interval $(0,1)\cup (2,\infty)$

Question:9 Prove that $y = \frac{4 \sin \theta }{(2+ \cos \theta )} - \theta$ is an increasing function of $\theta\: \: in\: \: [ 0 , \pi /2 ]$

Answer:

Given function is,
$f(x) = y = \frac{4 \sin \theta }{(2+ \cos \theta )} - \theta$

$f^{'}(x) = \frac{dy}{d\theta} = \frac{4 \cos \theta(2+\cos \theta) - (-\sin \theta)4\sin \theta) }{(2+ \cos \theta )^2} - 1$
$= \frac{8 \cos \theta+4\cos^2 \theta + 4\sin^2 \theta - (2+ \cos \theta )^2 }{(2+ \cos \theta )^2}$
$= \frac{8 \cos \theta+4(\cos^2 \theta + \sin^2 \theta) - 4- \cos^2 \theta - 4\cos \theta }{(2+ \cos \theta )^2}$
$= \frac{8 \cos \theta+4 - 4- \cos^2 \theta - 4\cos \theta }{(2+ \cos \theta )^2}$
$= \frac{4 \cos \theta-\cos^2 \theta }{(2+ \cos \theta )^2}$
Now, for $\theta \ \epsilon \ [0,\frac{\pi}{2}]$
$\\ 4 \cos \theta \geq \cos^2 \theta\\ 4 \cos \theta - \cos^2 \geq 0\\ and \ (2+\cos \theta)^2 > 0$
So, $f^{'}(x) > 0 \ for \ \theta \ in \ [0,\frac{\pi}{2}]$
Hence, $f(x) = y = \frac{4 \sin \theta }{(2+ \cos \theta )} - \theta$ is increasing function in $\theta \ \epsilon \ [0,\frac{\pi}{2}]$

Question:10 Prove that the logarithmic function is increasing on $( 0 , \infty )$

Answer:

Let logarithmic function is log x
$f(x) = log x$
$f^{'}(x) = \frac{1}{x}$
Now, for all values of x in $( 0 , \infty )$ , $f^{'}(x) > 0$
Hence, the logarithmic function $f(x) = log x$ is increasing in the interval $( 0 , \infty )$

Question:11 Prove that the function f given by $f ( x) = x ^2 - x + 1$ is neither strictly increasing nor decreasing on (– 1, 1).

Answer:

Given function is,
$f ( x) = x ^2 - x + 1$
$f^{'}(x) = 2x - 1$
Now, for interval $(-1,\frac{1}{2})$ , $f^{'}(x) < 0$ and for interval $(\frac{1}{2},1),f^{'}(x) > 0$
Hence, by this, we can say that $f ( x) = x ^2 - x + 1$ is neither strictly increasing nor decreasing in the interval (-1,1)

Question:12 Which of the following functions are decreasing on $0 , \pi /2$ $(A) \cos x \\(B) \cos 2x \\ (C) \cos 3x \\ (D) \tan x$

Answer:

(A)
$f(x) = \cos x \\ f^{'}(x) = -\sin x$
$f^{'}(x) < 0$ for x in $(0,\frac{\pi}{2})$
Hence, $f(x) = \cos x$ is decreasing function in $(0,\frac{\pi}{2})$

(B)
$f(x) = \cos 2x \\ f^{'}(x) = -2\sin2 x$
Now, as
$0 < x < \frac{\pi}{2}\\ 0 < 2x < \pi$
$f^{'}(x) < 0$ for 2x in $(0,\pi)$
Hence, $f(x) = \cos 2x$ is decreasing function in $(0,\frac{\pi}{2})$

(C)
$f(x) = \cos 3x \\ f^{'}(x) = -3\sin3 x$
Now, as
$0 < x < \frac{\pi}{2}\\ 0 < 3x < \frac{3\pi}{2}$
$f^{'}(x) < 0$ for $x \ \epsilon \ \left ( 0,\frac{\pi}{3} \right )$ and $f^{'}(x) > 0 \ x \ \epsilon \ \left ( \frac{\pi}{3} , \frac{\pi}{2}\right )$
Hence, it is clear that $f(x) = \cos 3x$ is neither increasing nor decreasing in $(0,\frac{\pi}{2})$

(D)
$f(x) = \tan x\\ f^{'}(x) = \sec^{2}x$
$f^{'}(x) > 0$ for x in $(0,\frac{\pi}{2})$
Hence, $f(x) = \tan x$ is strictly increasing function in the interval $(0,\frac{\pi}{2})$

So, only (A) and (B) are decreasing functions in $(0,\frac{\pi}{2})$

Question:13 On which of the following intervals is the function f given by $f ( x) = x ^{100} + \sin x - 1$ decreasing ?
(A) (0,1) (B) $\frac{\pi}{2},\pi$ (C) $0,\frac{\pi}{2}$ (D) None of these

Answer:

(A) Given function is,
$f ( x) = x ^{100} + \sin x - 1$
$f^{'}(x) = 100x^{99} + \cos x$
Now, in interval (0,1)
$f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is increasing function in interval (0,1)

(B) Now, in interval $\left ( \frac{\pi}{2},\pi \right )$
$100x^{99} > 0 \ but \ \cos x < 0$
$100x^{99} > \cos x \\ 100x^{99} - \cos x > 0$ , $f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is increasing function in interval $\left ( \frac{\pi}{2},\pi \right )$

(C) Now, in interval $\left ( 0,\frac{\pi}{2} \right )$
$100x^{99} > 0 \ and \ \cos x > 0$
$100x^{99} > \cos x \\ 100x^{99} - \cos x > 0$ , $f^{'}(x) > 0$
Hence, $f ( x) = x ^{100} + \sin x - 1$ is increasing function in interval $\left ( 0,\frac{\pi}{2} \right )$

So, $f ( x) = x ^{100} + \sin x - 1$ is increasing for all cases
Hence, correct answer is (D) None of these

Question:14 For what values of a the function f given by $f (x) = x^2 + ax + 1$ is increasing on
[1, 2]?

Answer:

Given function is,
$f (x) = x^2 + ax + 1$
$f^{'}(x) = 2x + a$
Now, we can clearly see that for every value of $a > -2$
$f^{'}(x) = 2x + a$ $> 0$
Hence, $f (x) = x^2 + ax + 1$ is increasing for every value of $a > -2$ in the interval [1,2]

Question:15 Let I be any interval disjoint from [–1, 1]. Prove that the function f given by $f ( x) = x + 1/x$ is increasing on I.

Answer:

Given function is,
$f ( x) = x + 1/x$
$f^{'}(x) = 1 - \frac{1}{x^2}$
Now,
$f^{'}(x) = 0\\ 1 - \frac{1}{x^2} = 0\\ x^{2} = 1\\ x = \pm1$

So, intervals are from $(-\infty,-1), (-1,1) \ and \ (1,\infty)$
In interval $(-\infty,-1), (1,\infty)$ , $\frac{1}{x^2} < 1 \Rightarrow 1 - \frac{1}{x^2} > 0$
$f^{'}(x) > 0$
Hence, $f ( x) = x + 1/x$ is increasing in interval $(-\infty,-1)\cup (1,\infty)$
In interval (-1,1) , $\frac{1}{x^2} > 1 \Rightarrow 1 - \frac{1}{x^2} < 0$
$f^{'}(x) < 0$
Hence, $f ( x) = x + 1/x$ is decreasing in interval (-1,1)
Hence, the function f given by $f ( x) = x + 1/x$ is increasing on I disjoint from [–1, 1]

Question:16 Prove that the function f given by $f (x) = \log \sin x$ is increasing on

$\left ( 0 , \pi /2 \right )\: \: and \: \: decreasing \: \: on \: \: \left ( \pi/2 , \pi \right )$
Answer:

Given function is,
$f (x) = \log \sin x$
$f^{'}(x) = \frac{1}{\sin x}\cos x = \cot x$
Now, we know that cot x is+ve in the interval $\left ( 0 , \pi /2 \right )$ and -ve in the interval $\left ( \pi/2 , \pi \right )$
$f^{'}(x) > 0 \ in \ \left ( 0,\frac{\pi}{2} \right ) \ and \ f^{'}(x) < 0 \ in \ \left ( \frac{\pi}{2} , \pi \right )$
Hence, $f (x) = \log \sin x$ is increasing in the interval $\left ( 0 , \pi /2 \right )$ and decreasing in interval $\left ( \pi/2 , \pi \right )$

Question:17 Prove that the function f given by f (x) = log |cos x| is decreasing on $( 0 , \pi /2 )$
and increasing on $( 3 \pi/2 , 2\pi )$

Answer:

Given function is,
f(x) = log|cos x|
value of cos x is always +ve in both these cases
So, we can write log|cos x| = log(cos x)
Now,
$f^{'}(x) = \frac{1}{\cos x}(-\sin x) = -\tan x$
We know that in interval $\left ( 0,\frac{\pi}{2} \right )$ , $\tan x > 0 \Rightarrow -\tan x< 0$
$f^{'}(x) < 0$
Hence, f(x) = log|cos x| is decreasing in interval $\left ( 0,\frac{\pi}{2} \right )$

We know that in interval $\left ( \frac{3\pi}{2},2\pi \right )$ , $\tan x < 0 \Rightarrow -\tan x> 0$
$f^{'}(x) > 0$
Hence, f(x) = log|cos x| is increasing in interval $\left ( \frac{3\pi}{2},2\pi \right )$

Question:18 Prove that the function given by $f (x) = x^3 - 3x^2 + 3x - 100$ is increasing in R.

Answer:

Given function is,
$f (x) = x^3 - 3x^2 + 3x - 100$
$f^{'}(x) = 3x^2 - 6x + 3$
$= 3(x^2 - 2x + 1) = 3(x-1)^2$
$f^{'}(x) = 3(x-1)^2$
We can clearly see that for any value of x in R $f^{'}(x) > 0$
Hence, $f (x) = x^3 - 3x^2 + 3x - 100$ is an increasing function in R

Question:19 The interval in which $y = x ^2 e ^{-x}$ is increasing is

(A) $( - \infty , \infty )$ (B) $( - 2 , 0 )$ (C) $( - 2 , \infty )$ (D) $( 0, 2 )$

Answer:

Given function is,
$f(x) \Rightarrow y = x ^2 e ^{-x}$
$f^{'}(x) \Rightarrow \frac{dy}{dx} = 2x e ^{-x} + -e^{-x}(x^{2})$
$xe ^{-x}(2 -x)$
$f^{'}(x) = xe ^{-x}(2 -x)$
Now, it is clear that $f^{'}(x) > 0$ only in the interval (0,2)
So, $f(x) \Rightarrow y = x ^2 e ^{-x}$ is an increasing function for the interval (0,2)
Hence, (D) is the answer

Benefits of NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2

Exercise 6.2 Class 12 Maths helps students to grasp the concepts in a better way.
NCERT solutions for Class 12 Maths chapter 6 exercise 6.2 is useful for the preparation of board exams that follows the NCERT Syllabus
Along with this students can also refer to the NCERT exemplar solutions of the same chapter for a good score.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Key Features Of NCERT Solutions for Exercise 6.2 Class 12 Maths Chapter 6

Comprehensive Coverage: The solutions encompass all the topics covered in ex 6.2 class 12, ensuring a thorough understanding of the concepts.
Step-by-Step Solutions: In this class 12 maths ex 6.2, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
Accuracy and Clarity: Solutions for class 12 ex 6.2 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
Conceptual Clarity: In this 12th class maths exercise 6.2 answers, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
Inclusive Approach: Solutions for ex 6.2 class 12 cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
Relevance to Curriculum: The solutions for class 12 maths ex 6.2 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. The number of examples given in the Class 12 NCERT Maths topic 6.3 is………...

7 examples are discussed in the NCERT topic decreasing and increasing function.

2. What is the topic discussed before increasing and decreasing function?

The topic 6.2 rates of change of quantities are discussed prior to increasing and decreasing function

3. Why do we study applications of derivatives?

The concepts of derivatives and their applications are used in various engineering and science domains for analysis purposes. So to build the basics of derivatives the NCERT Mathematics Books Classes 11 and 12 introduce the concepts of derivatives.

4. Name the topics discussed after NCERT Solutions for Class 12 Maths chapter 6 exercise 6.2?

Tangents and normal is the topic discussed after the exercise 6.2 Class 12 Maths

5. In the interval (0, pi/2) the function sinx is …………….

The function sinx is strictly increasing in the open interval (0, pi/2)

6. Whether f(x)=sinx is increasing or decreasing in (pi/2, pi)

If we look at the graph of sinx it can be seen that f(x) = sinx is strictly decreasing.

7. What is the nature of sinx in open interval (0, pi)?

Sinx is neither increasing nor decreasing in the given interval (0, pi)

8. Name the chapter coming after the application of derivatives in the NCERT book for Class 12 Maths

Integrals is introduced in chapter 7 of Class 12 NCERT Maths.

Also Read

NCERT Class 12 Maths Notes - Download Chapter wise Free PDFs

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

APOSS Inter Time Table 2025 - Check Andhra Pradesh Open School Exam Dates

Dec 19, 2024

CBSE Class 11 Date Sheet 2025 – Download Class 11th Exam Schedule for All Subjects

Dec 19, 2024

CBSE Class 12 Maths Syllabus 2024-25: Download PDF

Dec 19, 2024

UP Board Practical Exams 2025 - UPMSP High School and Inter Viva to Be Recorded to Ensure Transparency

Dec 19, 2024

JAC 12th Result 2024 Commerce OUT, Check Jharkhand 12th Commerce Result @jacresults.com

Dec 19, 2024

CBSE Class 12 English 2025: Expected Article Writing Questions to Prepare

Dec 17, 2024

Score Above 90% in CBSE Class 12 Board Exam 2025: 2-month Preparation Plan

Dec 17, 2024

CBSE Exam Rules for Class 10 and 12: New Guidelines For CBSE Exams 2024-25

Dec 13, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Admit Card

Result

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

View All School Exams

Certifications By Top Providers

My SQL Basics

Via Great Learning

Full-Stack Web Development

Via Masai School

Business Analytics Foundations

Via PW Skills

Digital Banking Business Model

Via State Bank of India

Full-Stack Android Development

Via Masai School

Machine Learning with Python a Practical Introduction

Via IBM

1115 courses

816 courses

394 courses

295 courses

Harvard University, Cambridge

98 courses

University of Michigan, Ann Arbor

83 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

Environmental Studies

History

Psychology

Artificial Intelligence

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Delaware, Newark

Newark, DE 19716

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Exams Required to Study in USA: GMAT, GRE, SAT, ACT, IELTS, PTE

9 min ⋆ Dec 19, 2024 06:12 AM IST

Countries Tightened Visa Rules for International Students in 2025

9 min ⋆ Dec 19, 2024 06:12 AM IST

PR in France for Indian and International Students 2025

11 min ⋆ Dec 19, 2024 05:12 AM IST

PR in USA for Indian Students in 2025

8 min ⋆ Dec 19, 2024 05:12 AM IST

Cheapest and Affordable Universities in France for International Students in 2025

12 min ⋆ Dec 19, 2024 05:12 AM IST

Study in Singapore for Indian Students in 2025

12 min ⋆ Dec 19, 2024 05:12 AM IST

Related E-books & Sample Papers

CBSE Class 12 Accountancy Question Papers 2024 (Code-PQ1RS/1) – All Sets (1, 2, 3)

35+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-QSS4R/4) – All Sets (1, 2, 3)

40+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-Q5QPS/5) – All Sets (1, 2, 3)

17+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code- PQ3RS/3) – All Sets (1, 2, 3)

6+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-PQ2RS/2) – All Sets (1, 2, 3)

5+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-PQ1RS/1) – All Sets (1, 2, 3)

6+ Downloads

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?

quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer

Jefferson 25 September,2024

i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

Re-evaluate Your Study Strategies:
- Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
- Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
- Practice Regularly: Consistent practice is key to mastering chemistry.
Consider Professional Help:
- Tutoring: A tutor can provide personalized guidance and support.
- Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.
Explore Alternative Options:
- Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
- Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.
Focus on NEET 2025 Preparation:
- Stay Dedicated: Continue your NEET preparation with renewed determination.
- Utilize Resources: Make use of study materials, online courses, and mock tests.
Seek Support:
- Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
- Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.

Read Complete Answer

Kanishka kaushikii 17 September,2024

i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer

Yuvan 30 August,2024

i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer

Ashvadha 12 July,2024

Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer

kumardurgesh1802 10 July,2024

View All

Stay up-to date with CBSE Class 12th News

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Central Board of Secondary Education Class 12th Examination

JEE Test Series

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Exercise 6.2 Class 12 Maths Chapter 10 - Application of Derivatives

NCERT Solutions For Class 12 Maths Chapter 6 Exercise 6.2

Pearson | PTE

Assess NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2

Application of Derivatives Class 12 Exercise 6.2

More About NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2

Benefits of NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2

Key Features Of NCERT Solutions for Exercise 6.2 Class 12 Maths Chapter 6

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Certifications By Top Providers

Explore Top Universities Across Globe

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Popular CBSE Class 12th Questions

Colleges After 12th

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Stay up-to date with CBSE Class 12th News

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

NVS

JNVST

Schools By Medium

By Ownership

By City

By State

Download Careers360 App

All this at the convenience of your phone

Scan and download the app