Nuclei Class 12th Notes - Free NCERT Class 12 Physics Chapter 13 Notes - Download PDF

NCERT Class 12 Physics Chapter 13 Notes: Download PDF

NCERT Class 12 Physics Chapter 13 Notes PDF offers a broad insight into atomic nuclei. It is a downloadable resource that includes the important concepts of nuclear structure, binding energy, radioactivity and nuclear reactions and is therefore good in preparing for boards of CBSE exams and other competitive examinations such as JEE and NEET. Get it wherever needed, whenever it is needed to revise easily and learn thoroughly.

Download PDF

NCERT Class 12 Physics Chapter 13 Notes

Chapter 13 of Class 12 Physics, Nuclei, discusses the structure, properties and behaviour of atomic nuclei. Some of the major concepts addressed in these notes include nuclear composition, binding energy, radioactivity, nuclear reactions, which provide the students a solid base for board exams and competitive tests such as JEE and NEET.

Introduction

Rutherford’s alpha (α) particle scattering experiment revealed that the entire positive charge and almost all the mass of an atom are concentrated in a tiny central region called the nucleus. The nucleus is made up of protons and neutrons.

• Protons are positively charged particles and contribute to both the charge and mass of the nucleus. Mass of proton, ${\mathrm{m}}_{\mathrm{p}}=1.6726\times {10}^{-27}\mathrm{kg}$

• Neutrons are neutral (uncharged) particles, but their mass is nearly equal to that of protons, so they also contribute to the nucleus's mass. Mass of neutron, ${\mathrm{m}}_{\mathrm{n}}=1.6749\times {10}^{-27}\mathrm{kg}$

The atomic number (Z) is the number of protons in the nucleus, and the mass number (A) is the total number of protons and neutrons:

Mass number (A) = Number of protons (Z) + Number of neutrons (A - Z)

An atom X with atomic number Z and mass number A is represented as: $Z_A^{}\mathrm{X}$

Atomic Masses

A small unit has been chosen to express the masses of atoms, nuclei, and fundamental particles ( electrons, protons, etc.) called the ‘atomic mass unit’ and is denoted by u. 1 u is defined as one-twelfth part of carbon (₆C¹²) atom. According to this definition, the mass of a carbon (₆C¹²) atom is exactly 12.00000...u

The mass of 1 gram-atom of carbon is 12 grams and it has N atoms, where N is Avogadro’s number. Thus, the mass of one gram of carbon is 12/N gram. According to the definition,

$\frac{1}{u}=\frac{1}{12}(\text{mass of one carbon atom})=\frac{1}{12}\left(\frac{12}{N}\mathrm{gram}\right)=\frac{1}{N}\mathrm{gram}$

But $\mathrm{N}=6.02\times {10}^{23}$

$\begin{array}{r}\therefore 1u=\frac{1}{N}=\frac{1}{6.02\times {10}^{23}}g=1.66\times {10}^{-24}g\\ 1u=1.66\times {10}^{-27}\mathrm{kg}\end{array}$

Nuclear Size

The volume of a nucleus is directly proportional to the number of nucleons in it, which is its mass number A. Thus, if R is the radius of a nucleus, then its volume is 4/3R³.

$\begin{array}{r}\frac{4}{3}\pi R^3\propto A\\ R\propto A^{\frac{1}{3}}\\ R=R_0{A}^{\frac{1}{3}}\end{array}$

Where R₀ is a constant. Experimentally, its value is 1.2 х 10⁻¹⁵ m. Nuclei of different atoms have different radii.

Nuclear Shape

Nuclei are regarded as spherical.

Nuclear Density

The density of the nuclei of all atoms is almost the same. The density of nuclei is 2 × 10¹⁷kgm⁻³ which is 10¹³ to 10¹⁴ times the density of ordinary matter.

Energy-Mass-Relation

The theory of relativity by Einstein proved that energy and mass are related to each other, and every substance has energy due to its mass also. If a substance loses an amount of Δm of its mass, an equivalent amount ΔE of energy is produced, where

$\mathrm{\Delta }E=(\mathrm{\Delta }m)c^2$

Where c is the speed of light. This is called ‘‘Einstein’s energy-mass equivalence relation”.

If we give ΔE energy to some matter, then according to the above relation, its mass will increase by Δm, where

$\mathrm{\Delta }m=\frac{\mathrm{\Delta }E}{c^2}$

Since the value of c is very high, the increase in mass Δm is very small. The conversion of energy into mass and mass into energy can be observed at the nuclear level in the phenomena known as pair production and pair annihilation.

Mass Defect and Binding Energy of Nucleus

The difference between the mass of the nucleons constituting a nucleus and the rest mass of the nucleus is called the mass defect Δm, i.e.,

Δm = (mass of protons + mass of neutrons ) - mass of the nucleus

Let us consider an atom of an element _zX^A. Its atomic mass number is A and its atomic number is Z. Thus, its nucleus has Z protons and (A - Z) neutrons. If m_p is the mass of a proton and m_n the mass of a neutron and m_N the mass of the nucleus, then the mass defect is

$\mathrm{\Delta }m=Z{m}_p+(A-Z)m_p-m_N$

This equation means that when Z free protons and ( A - Z) free neutrons come in from infinity and combine together to form the nucleus, an amount of Δm mass disappears. The disappeared mass reappears as equivalent energy Δmc², which is liberated during the formation of the nucleus. It is due to this energy that protons and neutrons remain bound in the nucleus. Conversely, an amount Δmc² of external energy is required to break the nucleus into protons and neutrons. This is called the binding energy of the nucleus. Thus, the Binding energy is defined as the minimum energy required to separate its nucleons and place them at rest at an infinite distance apart. Thus,

$BE=(\mathrm{\Delta }m)c^2=Z{m}_p+[(A-Z)m_n-m_N]c^2\dots \dots (i)$

The electron binding energy is, however, negligible in comparison to the nucleon binding energy. Thus,

$\begin{array}{r}m\left(z{X}^A\right)=m_N+Z{m}_e\\ m_N=m\left(z{X}^A\right)-Z{m}_e\end{array}$

Putting the value of $m_N$ in eqn (i), we get

$BE=Z(m_p+m_e)+[(A-Z)m_n-m\left(z{X}^A\right)]c^2\dots \dots (ii)$

But $m_p+m_e=m_{\mathrm{H,}}$ the mass of a hydrogen atom, which contains one proton and one electron. Thus

$BE=Z{m}_H+[(A-Z)m_n-m\left(Z^A{X}^A\right)]c^2$

This is the expression for the nuclear binding energy of an atom _zX^A in terms of atomic masses and neutron mass.

Eq (i) and Eq (ii) are identical because in Eqn (ii) masses of Z electrons appear in the first and the second the first and third terms, mutually cancel.

Since

$1u\times c^2=931.5\mathrm{MeV}$
The eq (ii) can also be written as

$BE=Z{m}_H+[(A-Z)m_n-m\left(Z_{}{X}^A\right)]\times 931.5\mathrm{MeV}$

Binding Curve

A graph between the average binding energy per nucleon and the mass number A of different nuclei is a curve called the Binding energy Curve.

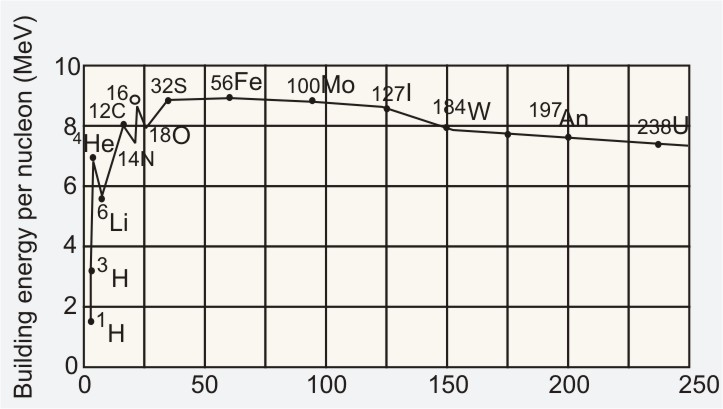
(i) The curve is almost a flat maximum roughly from A = 50 to A = 80, corresponding to an average BE/nucleon of above 8.5 MeV. So, the nuclei having a mass number between 50 and 80 are stable.

(ii) For nuclei having mass numbers above 80, the average BE/nucleon decreases slowly and drops to about 7.6 MeV for Uranium.

(iii) For nuclei having mass numbers below 50, the average BE/nucleon decreases and below 20 it decreases sharply. This shows that the nuclei having mass numbers below 20 are comparatively less stable.

(iv) Below A = 50, the curve does not fall continuously but has subsidiary peaks at ₈O¹⁶, ₆C^12, and ₂He⁴. This shows that these (even-even )nuclei are more stable than their intermediate neighbours.

(v) The curve shows that very heavy and very light nuclei have a lower average BE/nucleon than the nuclei of intermediate masses. If a very heavy nucleus ( such as U²³⁸ ) is separated into two lighter nuclei near the flat maximum of the curve, the BE/nucleon will increase by about 1 MeV. Hence, energy will be released in the process. This method of releasing nuclear energy by breaking up a heavy nucleus into two lighter nuclei of comparable masses is called nuclear fission; it is the basis of nuclear bombs and nuclear reactors.

Alternatively, if two or more very light nuclei (such as H²) are combined to form a heavier nucleus ( such as He⁴), the BE/nucleon will again increase, and now by a much greater amount than in the fission process. This will result in a much larger release of energy. This method of releasing nuclear energy is called nuclear fusion. It occurs inside the sun and other stars and is the source of their energy.

Nuclear Force

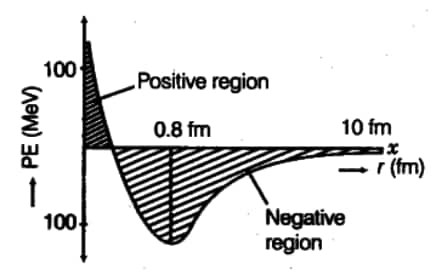
• The nuclear force is stronger than the Coulomb force or the gravitational force.

• The nuclear force will become a repulsive force when the distance between two nucleons exceeds a few femtometers.

• The nuclear forces between neutrons, proton-neutrons, and proton-protons are almost similar.

Radioactivity

The spontaneous emission of rays from a substance is called Radioactivity and such a substance is called a radioactive substance.

By experiment, Rutherford observed that the radiation has three types of rays: one which deflected towards the negative plate, a second which deflected towards the positive plate, and a third which was undeflected in the electric field. These are called alpha rays (α-rays), beta rays (β-rays), and gamma rays (γ-rays) , respectively. α-rays and β-rays are streams of particles; hence, they are called α- and β- particles. α- and β- particles are positively charged and negatively charged, respectively. The γ-rays are electrically neutral.

No radioactive substance emits both α- and β- particles simultaneously. Some substances emit α-particles and some others emit β-particles. γ-rays are emitted along with both α- and β- particles.

Nuclear Fission

Nuclear fission is a process in which a heavy nucleus, after capturing a neutron, splits up into two lighter nuclei of comparable masses. The product nuclei are called fission fragments; the process is accompanied by the release of a few fast neutrons and a huge amount of energy in the form of the kinetic energy of the fission fragments and of the release of neutrons, Gamma rays, etc. Nuclear fission is the basis of nuclear bombs and nuclear reactors. For example-

${92}_{}{U}^{235}+0_{}{n}^1\to {92}_{}{U}^{236}\to {56}_{}B{a}^{141}+{36}_{}K{r}^{92}+3_0{n}^1+Q$

Nuclear Fusion

When two or more very light nuclei moving at very high speeds are fused together to form a single nucleus, then the process is known as nuclear fusion. The mass of the product nucleus is less than the sum of the masses of the nuclei which were fused. The lost mass is converted into energy, which is released in this process. This property of light nuclei is shown by the binding energy curve, in which the average binding energy per nucleon rises sharply with an increase in mass number in the range of low mass number nuclei. For example

$1_{}{H}^1+1_{}{H}^2\to 1_{}{H}^3+1_{}{H}^1+4.0\mathrm{MeV}$ energy

Nuclear Reactor

A nuclear reactor is a device in which a self-sustaining controlled chain reaction is produced in fissionable material. It is thus a source of controlled energy which is utilised for many useful purposes.

Topics Important for Competitive Exams not in NCERT

There are a number of topics crucial for competitive exams, such as JEE and NEE,T which are not covered in the NCERT textbook. Concepts include alpha, beta and gamma decay, law of radioactive decay, Rutherford and Soddy's Law and half-life. You can find detailed notes for these below.

Alpha Decay

The emission of an Alpha particle from a radioactive nucleus is called Alpha decay. It generally occurs in nuclei containing 210 or more nucleons. These new particles are so large that the short-range nuclear forces holding the nucleons together are unable to counterbalance the electrostatic repulsion among a large number of protons in them. Therefore, in an attempt to achieve greater stability by reducing their size, they emit Alpha particles

An alpha particle is a helium nucleus whose atomic number is 2 and mass number is 4. Therefore, when an Alpha particle is emitted from the nucleus of a radioactive atom, the atomic number z decreases by 2 and the mass number decreases by 4. Thus, the atom is converted into an atom of some other element. For example,

$\begin{array}{rl}{92}_{}{U}^{238}& \to 2_{}H{e}^4+{90}_{}T{h}^{234}\\ (\alpha -\text{particle})\end{array}$

$\alpha$ - decay is represented by the equation

$\underset{\mathit{\text{parent}}}{\underset{\mathit{\text{nucleus}}}{Z_A^{}X}}\to \underset{\mathit{\text{daughter}}}{\underset{\mathit{\text{nucleus}}}{{Z-2}_{A-4}^{}Y}}+\underset{\mathit{\text{alpha}}}{\underset{\mathit{\text{particle}}}{2_4^{}\text{He}}}+\underset{\mathit{\text{energy}}}{\underset{\mathit{\text{released}}}{Q}}$

Since α-particle has high binding energy, its formation within the nucleus causes the release of sufficient energy that becomes available to escape. The energy is shared by the daughter nucleus Y and the α-particle. Mostly, the energy is taken by the α-particle.

Beta Decay

Emission of a β - particle from a radioactive nucleus is called beta decay. It generally occurs in nuclear matter having a neutron /proton ratio higher than that for stable nuclei.

At the time of emission of β-particle, a neutron in the nucleus is converted into a proton and this process is a new particle and the new particle antineutrino, is also produced. The emission is represented by the following equation

$\underset{(\mathit{\text{neutron}})}{0_1^{}n}\to \underset{(\mathit{\text{proton}})}{1_1^{}H}+\underset{(\mathit{\text{electron}})}{{-1}_0^{}\beta }+\left(\overline{\nu }\right)$

Since in β emission, a neutron is converted into a proton, the neutron-proton ratio decreases

The antineutron is a particle with zero rest mass and zero charge. Therefore, a beta particle is emitted from the nucleus of a radioactive atom and the atomic number Z (the number of protons) increases by one unit. But the total number of nucleons remains constant.

Gamma decay

The emission of gamma rays along with the emission of alpha or beta particles from a radioactive source is called gamma decay.

To explain the emission of Gamma rays from the nucleus, it was assumed that, as in an atom, there are discrete energy levels within the nucleus also. When an Alpha or beta particle is emitted from the parent nucleus, the daughter nucleus is left in an excited state. The excited nucleus returns to its normal state by emitting its excess energy in the form of gamma rays.

For example, the unstable nucleus ₂₇Co⁶⁰ beta-decays to an excited nucleus ₂₈Ni⁶⁰ which in turn reaches its stable ground state by emitting Gamma photons of energy 1.17 MeV and 1.33MeV into two transitions. The existence of energy levels in the nucleus has been experimentally confirmed.

Radioactive Decay Law and Decay Constant

We know that a radioactive substance emits α- particles or β- particles and also γ- rays. The atomic weight and atomic number are changed. Thus, the original radioactive atom is decayed and an atom of some new element is born. This phenomenon is called “ Radioactive decay”.

For example, when an α- particle is emitted from the uranium atom, it is converted into a thorium atom.

${92}_{238}^{}U\to \underset{(\alpha \text{-- particle})}{2_4^{}\text{He}}+{90}_{234}^{}\text{Th}$

Thorium is also radioactive, and by emitting a $\beta$-particle, it is converted into a protactinium atom.

${90}_{234}^{}Th\to \underset{(\beta \text{- particle})}{{-1}_0^{}\beta }+{}_{91}^{234}Pa+\underset{(\mathit{\text{anti-neutrino}})}{\overline{\nu }}$

The radioactive decay continues until a stable atom is obtained.

Rutherford and Soddy's Law for Radioactive Decay

The rate of decay or disintegration of radioactive atoms is proportional to the number of atoms present at any given time.

Let N be the total number of atoms in a radioactive substance at any given time t.

Let dN be the no that disintegrates in a short interval dt. Then the rate of disintegration (- dN/dt) is proportional to N, i.e.,

$-\frac{dN}{dt}=\lambda N$

It is a constant known as the decay constant.

$\frac{dN}{N}=-\lambda dt$

On integrating,

${\log }_{e}N=-\lambda t+C$

C is constant. To determine C, apply the initial conditions. Let there be N₀ atoms, in the beginning, i.e., N = N₀ at t = 0. Then,

${\log }_e{N}_0=C$

Putting this value in the above equation, we get

$\begin{array}{r}{\log }_{e}N=-\lambda t+{\log }_e{N}_0\\ {\log }_{e}N-{\log }_e{N}_0=-\lambda t\\ {\log }_e\frac{N}{N_0}=-\lambda t\\ N=N_0{e}^{-\lambda t}\end{array}$

Here N₀ and N are the no. of atoms in a radioactive substance at time t = 0 and after time t, respectively. According to this equation, the decay of radioactive substances is exponential.

Half-Life

The half-life of radioactive material is the time taken by it to decrease to half of its initial value. The half-life of a radioactive substance is constant, but it is different for different substances.

The relation between the half-life and decay constant

Let N₀ be the no. of atoms present in a radioactive substance at time t =0 and be the no. at a later time t. Then

$N=N_0{e}^{-\lambda t}$

If the half-life of the substance is T, then at time t = T, the no. of atoms left will be N₀ /2, so, on putting these values in the above eqn, we get

$\begin{array}{r}\frac{N_0}{2}=N_{0e^{-\lambda t}}\\ \frac{1}{2}=e^{-\lambda t}\\ e^{\lambda t}=2\\ \lambda t={\log }_{e}2\\ T=\frac{{\log }_{e}2}{\lambda }=\frac{0.6931}{\lambda }\end{array}$

This is the relation between half-life and decay constant.

The activity of a Radioactive substance

The number of decay or disintegration per second of a radioactive substance is called the activity ( R ) of the substance. I.e.,

$R=\frac{dN}{dt}$

The rate of decay of radioactive atoms at any instant is proportional to the number of atoms present at that instant.

$\begin{array}{r}-\frac{dN}{dt}\propto N\\ -\frac{dN}{dt}=\lambda N\end{array}$

Therefore, the activity of the substance at any instant is also proportional to the no. of its atoms left at that instant. Thus,

$\begin{array}{r}R\propto N\\ R=\lambda N\end{array}$

Initially, at t = 0, the no. of atoms in a substance is N₀, and the half-life of the substance is T. Then, after one half-life, the no. of atoms at t = T is

$N=\frac{N_0}{2}=N_0{\left(\frac{1}{2}\right)}^1$

After two half-lives, the no. of atoms left will be N₀/4, i.e., t = 2T, the no. of atoms left is

$N=\frac{N_0}{4}=N_0{\left(\frac{1}{2}\right)}^2$

Thus, the no. of atoms left after n half-lives is given by

$N=N_0{\left(\frac{1}{2}\right)}^n$

The no. of atoms of a radioactive activity of a substance decreases with time.

Average or Mean Life of A Radioactive Substance

The mean life of a radioactive substance is the expected life of the given sample. It is denoted by $\tau$.

The reciprocal of the decay constant is the half-life of a radioactive substance.

$\tau =\frac{1}{\lambda }$

But

$\lambda =\frac{T}{0.6931}$

where T is the half-life of the substance.

$\tau =\frac{T}{0.6931}=1.443T$

Mean life is longer than half-life.

Nuclei: Previous year Question and Answer

Q.1 The nuclear radius of ${13}_{27}^{}\mathrm{Al}$ is $3.6\text{fermi}$. Find the nuclear radius of ${29}_{64}^{}\mathrm{Cu}$.

Answer:

$\begin{array}{r}\frac{r_1}{r_2}={\left(\frac{A_1}{A_2}\right)}^{\frac{1}{3}}\\ \frac{3.6\text{fermi}}{r_2}={\left(\frac{27}{64}\right)}^{\frac{1}{3}}\\ \frac{3.6\text{fermi}}{r_2}=\frac{3}{4}\\ r_2=3.6\times \frac{4}{3}=4.8\mathrm{fermi}\end{array}$
Hence, the answer is $4.8\mathrm{fermi}$.

Q.2 Plot a graph showing the variation of the potential energy of a pair of nucleons as a function of their separation. Also indicate the regions where the force is (i) attractive and (ii) repulsive. Write two characteristic properties of the nuclear force.

Answer:

In the graph,

$\Rightarrow$ For a separation greater than $r_0$, the force is attractive.

$\Rightarrow$ For a separation less than $r_0$, the force is strongly repulsive.

Characteristic properties of the nuclear force are-

$\Rightarrow$The nuclear force does not depend on the electric charge.

$\Rightarrow$ The nuclear force between two nucleons falls rapidly to zero as their distance is more than a few fermers.

$\Rightarrow$ The nuclear force is much stronger than the Coulomb force acting between the charges or the gravitational forces between masses.

Q.3 Distinguish between nuclear fission and fusion. Explain how the energy is released in both processes.

Answer:

$\to$ In nuclear fission, a heavier nucleus splits into two lighter nuclei.

$0_1^{}\mathrm{n}+{92}_{236}^{}\mathrm{U}\to {56}_{144}^{}\mathrm{Ba}+30_1^{}\mathrm{n}+{36}_{89}^{}\mathrm{kr}$

$\to$ In nuclear fusion, two light nuclei combine to form a heavier nucleus.

$4_1^1\mathrm{H}\to 2_4^{}\mathrm{He}+2v+6y+26\cdot 7\mathrm{mev}+2e-$

In both cases, the mass of products is slightly less than that of the mass of original nuclei. This difference in mass is converted to energy.

Importance of NCERT Class 12 Physics Chapter 13 Notes

Basics of Nuclear Physics

• It is crucial to understand what a nucleus is to be able to understand nuclear physics concepts, such as fission, fusion, and radioactivity.

Energy Science Applications

• Learn about energy generation, nuclear reactors, and nuclear power principles.

CBSE Board Exam Relevance

• Commonly used in Class 12 Physics exams; useful in numerical and theoretical questions.

Competitive Exam Prep

• Critical to JEE, NEET, and other entrance exams and questions about binding energy, half-life, and laws of decay.

Learning Atomic Structure

• It expands on the concept of atoms and assists in understanding matter on a fundamental level.

Radioactivity and Decay Concepts

• Essential to the understanding of alpha, beta, and gamma decay, and associated calculations.

Nuclear Reactions & Energy Transformation

• Covers fission and the fusion process, students learn how energy changes in a nuclear reaction.

Modern Physics

• This is an introductory course to more specialised studies in the fields of quantum mechanics and particle physics.

NCERT Class 12 Notes Chapterwise

Physics chapter wise notes of Class 12 NCERT cover the syllabus in a systematic and simple way which is easy to understand covering every single chapter of the syllabus. The notes can assist the students in polishing their ideas, rehearsing, and performing well in the CBSE board exams, the competitive exams such as JEE, and NEET. The chapter-by-chapter notes are clear, easy-to-follow with important formulas and illustrative diagrams, therefore, they make a good companion of effective learning and a fast revision.

Subject-Wise NCERT Exemplar Solutions

• NCERT Exemplar Class 12 Solutions
• NCERT Exemplar Class 12 Maths
• NCERT Exemplar Class 12 Physics
• NCERT Exemplar Class 12 Chemistry
• NCERT Exemplar Class 12 Biology

Subject-Wise NCERT Solutions

• NCERT Solutions for Class 12 Mathematics
• NCERT Solutions for Class 12 Chemistry
• NCERT Solutions for Class 12 Physics
  NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus