NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 8 Notes: Download PDF

NCERT Class 12 Physics Chapter 8 Notes PDF can be downloaded to study Electromagnetic Waves anywhere, and anytime. The PDF has good explanations, important formulas, and diagrams, making it ideal for revision and exam preparation for CBSE, JEE, and NEET.

Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves

NCERT Class 12 Physics Chapter 8 Notes on Electromagnetic Waves clearly explain how changing electric and magnetic fields can generate waves that will propagate in empty space. These notes make complex concepts easier to comprehend. These notes are great resources for the CBSE board exam and entrance exams such as JEE and NEET. These notes have important formulas, diagrams, and key points that will help you revise easily.

Displacement Current

"Displacement current is a current which is produced due to the rate of change of electric flux with respect to time". Displacement current is given by

$I_d={\epsilon }_0\frac{d}{dt}\left({\varphi }_E\right)$

Maxwell’s Equations

Maxwell put together the basic laws of electricity and magnetism is that, Gauss’ law of electricity, Gauss’ law of magnetism, Faraday’s law of electromagnetic induction, and Ampere-Maxwell’s Circuital law in the form of four fundamental equations, known as Maxwell’s equations.

On the basis of these equations, Maxwell anticipated the existence of electromagnetic waves.

1. Gauss’ law of electricity:- It states that the electric flux through any closed surface is equal to 1/?₀ times the net charge enclosed by the surface.
   $\oint \overrightarrow{E}\cdot d\overrightarrow{s}=\frac{q}{{ϵ}_0}$
   This equation is called Maxwell’s first equation. This equation is true for both moving and stationary charges.

2. Gauss’s law of magnetism:- It states that the magnetic flux through any closed surface is zero.
   $\oint \overrightarrow{B}\cdot d\overrightarrow{S}=0$
   This equation is called Maxwell’s second equation. It signifies that free magnetic poles do not exist. This equation also signifies that magnetic lines of force cannot start from a point nor end at a point, that is they are closed curves.

3. Faraday’s laws of Electromagnetic induction:- It asserts that the negative rate of change of magnetic flux across a circuit is equal to the induced emf set up in the circuit.
   $e=-\frac{d{\varphi }_B}{dt}$
   Since emf can be defined as the line integral of the electric field, the above relation can be expressed as
   $\oint \overrightarrow{E}\cdot d\overrightarrow{l}=-\frac{d{\varphi }_B}{dt}$
   The line integral of the electric field along a closed channel is therefore equal to the rate of change of magnetic flux through the surface bounded by that closed path, according to the law.
   This equation is called Maxwell's third equation. It signifies that the electric field is produced by a changing magnetic field.

4. Ampere-Maxwell’s Circuital law:- It states that the line integral of the magnetic field along a closed path is equal to μ₀ times the total current linked with the surface bounded by that closed path.

   $\oint \overrightarrow{B}\cdot d\overrightarrow{l}={\mu }_0(i+i_d)$
   Where $i_d={ϵ}_{0}A\frac{dE}{dt}$

This equation is known as Maxwell’s fourth equation. It signifies that a conduction current, as well as a changing electric field, produces a magnetic field.

Electromagnetic Waves

Sources of electromagnetic waves

"The waves that are produced by accelerated charged particles and composed of electric and magnetic fields vibrating transversely and sinusoidally perpendicular to each other and to the direction of propagation are called electromagnetic waves or electromagnetic radiations."

These waves are produced in the following physical phenomena :
(i) An electric charge at rest produces only an electrostatic field around it.
(ii) A charge moving with uniform velocity (i.e. steady current) produces both electric and magnetic fields; here magnetic field does not change with time, hence it does not produce time time-varying electric field.
(iii) An accelerating charge produces both an electric field and a magnetic field, which vary with space and time which forming an electromagnetic wave.
(iv) An accelerating charge (in case of LC oscillation) emits an electromagnetic wave of the same frequency as the frequency of the accelerating charge (i.e., the frequency of the oscillating LC circuit)
(v) An electron orbiting around its nucleus in a stationary orbit does not emit an electromagnetic wave. It will emit only during the transition from a higher energy orbit to a lower energy orbit.
(vi) An electromagnetic wave ( $X$-ray) is produced when a high-speed electron enters into target of high atomic weight.
(vii) Electromagnetic wave ( $\gamma$-rays) is produced during the de-excitation of the nucleus in radioactivity.

Nature of electromagnetic waves

(i) It is produced by an accelerated charge (e.g., X-ray) and an oscillating charge (e.g., LC oscillation).
(ii) It travels in free space with speed equal to $3\times {10}^8\mathrm{m}/\mathrm{s,}$ which is given by $c=\frac{1}{\sqrt{{\mu }_0{\epsilon }_0}}$.
(iii) These waves do not require a material medium for their propagation.
(iv) In these waves, $\overrightarrow{E}$ and $\overrightarrow{B}$ vary sinusoidally. $\overrightarrow{E}$ and $\overrightarrow{B}$ become maximum at the same place and at the same time, but perpendicular to each other as well as to the direction of propagation. Therefore, the phase difference between the two fields is zero. The amplitude of electric and magnetic fields is related to each other as $c=\frac{E_0}{B_0}$. The direction of propagation can be determined by $\overrightarrow{E}\times \overrightarrow{B}$.

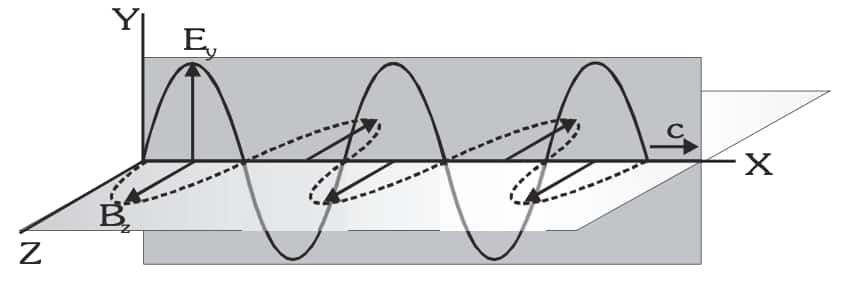
(v) The velocity of an electromagnetic wave in a medium is decided by the electric and magnetic properties of the medium, not by the amplitude of the electric and magnetic field vectors.

The speed of an electromagnetic wave in a medium is $v=\frac{1}{\sqrt{\mu \epsilon }}$.
(vi) The energy carried by an electromagnetic wave is equally divided between the electric field and the magnetic field. Total average energy density $U=\frac{1}{2}{\epsilon }_0{E}_0^2=\frac{1}{2}\frac{B_0^2}{{\mu }_0}$.
(vii) The electric field vector of an electromagnetic wave produces an optical effect, hence it is also known as the light vector.
(viii) An electromagnetic wave is not deflected by the electric field as well as the magnetic field because it consists of uncharged particles called photons.
(ix) Intensity of an electromagnetic wave is defined as "energy crossing per second per unit area perpendicular to the direction of propagation of the electromagnetic wave."

Average intensity is given by
$I=\frac{1}{2}{\epsilon }_0{E}_0^{2}c$ or ${\epsilon }_0{E}_{\text{r.m.s.}}^{2}c$ (in terms of electric field)
$$

$I=\frac{1}{2}\frac{B_0^2}{{\mu }_0}c=\frac{B_{\mathrm{rms}}^2}{{\mu }_0}\times c$ (in terms of magnetic field)

Relation Between Magnitudes of Vector E and Vector B in Free Space

Let a sinusoidal electromagnetic wave be propagating in free space along the positive direction of the X-axis with wave no. k and angular frequency ?. Then, the magnitudes of vector E and vector B acting along Y- and Z-axis, respectively, vary with x and t and can be written as

$\begin{array}{ll}E=E_0\sin (\omega t-kx)& \dots \dots (i)\\ B=B_0\sin (\omega t-kx)& \dots \dots (ii)\end{array}$

Where E₀ and B₀ are the maximum values of E and B, respectively.

$k=\frac{2\pi }{\lambda },\omega =2\pi v$

Here λ is the wavelength and v is the frequency of the wave.

$\therefore \frac{\omega }{k}=\frac{2\pi v}{2\pi /\lambda }=v\lambda =c$

c is the speed of the electromagnetic wave, which is the speed of light in free space. From eqn (i),

$\frac{\partial E}{\partial x}=-kx\cos (\omega t-kx)$

From eqn (ii),

$\frac{\partial B}{\partial t}=\omega B_0\cos (\omega t-kx)$

Putting these values in this relation

$\frac{\partial \overrightarrow{E}}{\partial x}=-\frac{\partial \overrightarrow{B}}{\partial t}$

we get

$\begin{array}{r}kx\cos (\omega t-kx)=\omega B_0\cos (\omega t-kx)\\ \frac{E_0}{B_0}=\frac{\omega }{k}=c\end{array}$

Since E and B are in the same phase.

$\frac{E}{B}=c$

At any point in space. Thus, the ratio of the magnitude of the electric field and the magnetic field equals the speed of light in free space.

Energy Density in Electromagnetic Waves

The energy density in an electric field E in a vacuum is ϵ₀E²/2, and that in a magnetic field B is B²/2μ₀. Thus, the energy density associated with an electromagnetic wave is

$u=\frac{1}{2}{ϵ}_0{E}^2+\frac{1}{2}\frac{B^2}{{\mu }_0}$

An electromagnetic wave propagating along the X-axis and the magnitude of vector E and vector B, acting along the Y- and Z-axes, respectively, can be written as

$E=E_0\sin (\omega t-kx)$ and $B=B_0\sin (\omega t-kx)$

Where E₀ and B₀ are the maximum values of E and B, respectively. Putting these values in Eq. (i), we get

$u=\frac{1}{2}{ϵ}_0{E}_0^2{\sin }^2(\omega t-kx)+\frac{1}{2}\frac{B_0^2}{{\mu }_0}{\sin }^2(\omega t-kx)$

The time average of sin² over any whole number of cycles is ½. Therefore, the average energy density of an e.m. wave is

$\overline{u}=\frac{1}{2}{ϵ}_0{E}_0^2+\frac{1}{2}\frac{B_0^2}{{\mu }_0}$

Here ϵ₀E²/2 is the average kinetic energy density u_e and B²/2μ₀ is the average magnetic density u_m.

Electromagnetic Spectrum

Maxwell predicted the existence of electromagnetic waves.
The electromagnetic wave was experimentally discovered by Hertz.
At the end of the nineteenth century, visible light, ultraviolet, infrared, X-rays and $\gamma$-rays had also been discovered. We now know that electromagnetic waves include (i) $\gamma$-rays, (ii) X-rays, (iii) ultraviolet rays, (iv) visible light, ( $\mathbf{v}$ ) infrared, (vi) microwaves, (vii) radiowaves.
"The orderly distribution of electromagnetic radiations according to their frequency (or wavelength) is called electromagnetic spectrum".

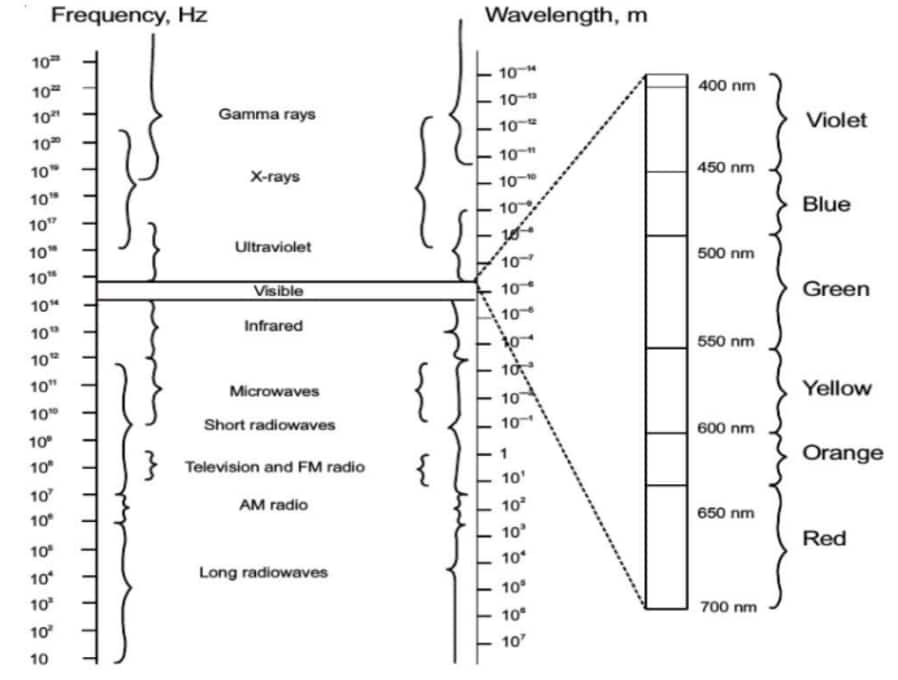
(i) Radio waves

• It is produced by the accelerated motion of charges in conducting wires. (i.e., by an oscillating electric circuit).
• Its frequency range is 500 kHz to about 1000 MHz
• Its wavelength range is $\approx {10}^{-2}\mathrm{m}$ to ${10}^4\mathrm{m}$.
• They are reflected, refracted and diffracted, used in radio and TV communication.

(ii) Microwaves

• It is produced by special vacuum tubes (called Klystrons, Magnetrons and Gunn diodes)
• Its frequency range is $\approx 1\mathrm{GHz}$ to 300 GHz
• Uses:
  (a) It is used in radar system for aircraft navigation.
  (b) It is used to detect the speed of a tennis ball, a cricket ball, automobile.
  (c) It is used in microwave ovens.

(iii) Infrared Waves

• It is produced by hot bodies, i.e. vibrations of atoms and molecules. (Hence also called heat waves).
• It is not detected by the human eye, but a snake can detect it.
• These waves are readily absorbed by water, ${\mathrm{CO}}_2,{\mathrm{NH}}_3$ etc.
• Its frequency range is ${10}^{11}\mathrm{Hz}$ to ${10}^{14}\mathrm{Hz}$.
• Its wavelength lies between $1\mathrm{mm}-700\mathrm{nm}$.
• It is detected by thermopiles, bolometers, and infrared photographic film.
• Uses:
  (a) An infrared lamp is used in physical therapy, i.e. to treat muscular strain.
  (b) It is responsible for keeping the average temperature through the greenhouse effect.
  (c) Infrared detectors are used in Earth satellites, both for military purposes and to observe the growth of crops.

(iv) Visible Light

• It is a narrow range of the electromagnetic spectrum
• It is produced by atomic excitation
• Its frequency range from $4\times {10}^{14}\mathrm{Hz}$ to about $7\times {10}^{14}\mathrm{Hz}$
• Its wavelength lies between 700 nm to 400 nm
• The visible light emitted or reflected from the objects around us provides us with information about the world.
• It is detected by the eyes, photocells, and photographic film.

(v) Ultraviolet Rays

• It is produced by the sun, special lamps and very hot bodies.
• Its frequency lies between $8\times {10}^{14}\mathrm{Hz}$ to $5\times {10}^{16}\mathrm{Hz}$.
• Its wavelength lies between 400 nm to 0.6 nm.
• It is detected by photocells, photographic film.
• Most of the ultraviolet radiations coming from the sun are absorbed by the ozone layer in the Earth's atmosphere.
• The UV rays in large quantities produce harmful effects on human beings, causing the production of melanin, tanning of the skin.
• It is absorbed by the ordinary glass.
• Uses:
  (a) Due to its short wavelength, it can be focused into a very narrow beam, which is used for high precision applications e.g., LASIK (laser-assisted in situ keratomileusis) eye surgery.
  (b) UV lamps are used to kill germs in water purifiers.
  (c) To destroy the bacteria and to sterilise the surgical instruments.
  (d) In fingerprint technology.

(vi) X-rays

• Its frequency order is ${10}^{16}\mathrm{Hz}$ to ${10}^{21}\mathrm{Hz}$.
• Its wavelength lies between 10 nm to ${10}^{-4}\mathrm{nm}$.
• It is produced in a tube called a modern X-ray tube.
• It is detected by photographic film, Geiger tubes and an ionisation chamber.
• X-rays are used as a diagnostic tool in medicine and as a treatment for certain forms of cancer.
• In engineering, it is used for detecting faults, cracks, flaws and holes.
• It is used for detecting pearls in oysters, defects in rubber tyres, and gold.

(vii) Gamma rays

• It is high-frequency radiation which is produced in nuclear reactions they are emitted by radioactive nuclei.
• Its frequency range is ${10}^{18}\mathrm{Hz}-{10}^{22}\mathrm{Hz}$.
• Its wavelength is $<{10}^{-3}\mathrm{nm}$. From about ${10}^{-10}\mathrm{m}$ to less than ${10}^{-14}\mathrm{m}$.
• It is detected by photographic film, Geiger tubes, ionisation chamber.
• They show phosphorescence, fluorescence, polarisation, and diffraction.
• They have very high penetrating power.
• They are used for cancer therapy.
• They provide important information regarding nuclear structure.

Electromagnetic Waves: Previous Year Question and Answer

Q1: A charged particle oscillates about its mean equilibrium position with a frequency of 109 Hz. The electromagnetic waves produced:

a) fall in the region of radio waves

b) will have a wavelength of 0.3 m

c) will have a frequency of 109 Hz

d) will have a frequency of 2 × 109 Hz

Answer:

a. fall in the region of radio waves
b. will have a wavelength of 0.3 m
C. will have a frequency of 109 Hz

Here, the particle that produces electromagnetic waves of frequency is equal to the frequency at which it oscillates about its mean equilibrium position.

So, the frequency of electromagnetic waves produced by the charged particle is $v=109 \mathrm{~Hz}$.
Wavelength $(\lambda)=c / v=3 \times 108 / 109=0.3 m$
The 109 Hz frequency falls under the radio wave region.

Hence, the answer are the options a, b and c..

Q2: An EM wave radiates outwards from a dipole antenna, with $E_0$ as the amplitude of its electric field vector. The electric field E_0, which transports significant energy from the source, falls off as

(a) $\frac{1}{r^3}$

(b) $\frac{1}{r}$

(c) $\frac{1}{r^2}$

(d) remains constant

Answer:

A diode antenna radiates the electromagnetic waves outward. The amplitude of the electric field vector falls inversely with the distance (r) from the antenna

From a dipole antenna, the electromagnetic waves are radiated outwards. The amplitude of the electric field vector $E_0$, which transports significant energy from the source, falls off inversely as the distance $r$ from the antenna, i.e., $E_0 \propto \frac{1}{r}$.

Hence, the answer is option (b).

Q3: A linearly polarised electromagnetic wave given as $E=E_0 \hat{i} \cos (k z-\omega t)$ is incident normally on a perfectly reflecting infinite wall at $z=a$. Assuming that the material of the wall is optically inactive, the reflected wave will be given as:

(a) $E_r=E_0 \hat{i} \cos (k z+\omega t)$

(b) $E_r=-E_0 \hat{i} \cos (k z+\omega t)$

(c) $E_r=-E_0 \hat{i} \cos (k z-\omega t)$

(d) $E_r=E_0 \hat{i} \sin(k z+\omega t)$

Answer:

A wave used to be the same, rather its phase changes by 180° or π radian when it is reflected from a denser medium or wall that is perfectly reflecting and made with optically inactive material.

$E_r=E_0 \hat{i} \cos (k z+\omega t)$

Hence, the answer is the option (a).

Importance of Electromagnetic Waves Class 12 Notes

Quick Reviewing Tool for Exams

• The NCERT Class 12 Physics Chapter 8 Notes PDF gives students a quick review of electromagnetic wave concepts like displacement current, properties of EM waves and electromagnetic spectrum in a simpler way.
• Great for last-minute board exam revision, and a great revision tool for JEE and NEET.

Includes All Relevant Derivations and Formulae

• The Electromagnetic Waves Class 12 Notes also include all relevant derivations and formulae in a simple way.
• Now students could easily learn the formulas associated with wave speed, displacement current and Maxwell's equations.

Improves Conceptual Clarity

• The easy-to-read context of the NCERT physics notes for Class 12 Chapter 8 reinforces some of the core concepts like wave propagation, nature of EM waves and practical applications in everyday life.
• Very helpful for developing a strong conceptual understanding of physics.

Useful for Competitive Examinations (JEE/NEET)

• The notes for Class 12 Chapter 8 Electromagnetic Waves provide the required preparation for competitive exams.
• Includes previous year questions and solved examples. Very useful for JEE Main and JEE Advanced, and NEET physics preparation.

Well-Organised and Easy to Memorise

• NCERT Class 12 Chapter 8 Notes PDF is systematically presented in terms of definitions, key points and diagrams.
• This allows for orderliness and therefore makes revising topics - even complex ones like the electromagnetic spectrum - easier to retain.

NCERT Class 12 Notes Chapterwise

The NCERT Class 12 Physics Notes chapterwise links provide quick access to well-structured revision material for every chapter. These notes cover key formulas, definitions, diagrams, and solved examples, making them the perfect resource for CBSE board exams, JEE, and NEET preparation.

Subject Wise NCERT Exampler Solutions

• NCERT Exemplar Class 12 Solutions
• NCERT Exemplar Class 12 Maths
• NCERT Exemplar Class 12 Physics
• NCERT Exemplar Class 12 Chemistry
• NCERT Exemplar Class 12 Biology

Subject Wise NCERT Solutions

• NCERT Solutions for Class 12 Mathematics
• NCERT Solutions for Class 12 Chemistry
• NCERT Solutions for Class 12 Physics
• NCERT Solutions for Class 12 Biology

NCERT Books and Syllabus