• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Exemplar Class 12 Physics Solutions Chapter 2 Electrostatic Potential and Capacitance

NCERT Exemplar Class 12 Physics Solutions Chapter 2 Electrostatic Potential and Capacitance

#CBSE Class 12th
Vishal kumarUpdated on 10 Jul 2025, 01:19 AM IST

Have you ever thought how the lightning on the thunderstorm can illuminate the entire sky? This spectacular phenomenon is a strong consequence of electrostatic problems-- huge electric charges accumulating and then exploding. This natural phenomenon is discussed in Class 12 Physics Chapter 2: Electrostatic Potential and Capacitance which deals with the interaction between charged particles and storage and transfer of energy in electric fields.

This Story also Contains

  1. NCERT Exemplar Class 11 Physics Solutions Chapter 2: MCQI
  2. NCERT Exemplar Class 11 Physics Solutions Chapter 2: MCQII
  3. NCERT Exemplar Class 11 Physics Solutions Chapter 2: Very Short Answer
  4. NCERT Exemplar Class 11 Physics Solutions Chapter 2: Short Answer
  5. NCERT Exemplar Class 11 Physics Solutions Chapter 2: Long Answer
  6. Main Topics of NCERT Exemplar Class 12 Physics Solutions Chapter 2
  7. NCERT Exemplar Class 12 Physics Solutions Chapter-Wise
NCERT Exemplar Class 12 Physics Solutions Chapter 2 Electrostatic Potential and Capacitance
NCERT Exemplar Class 12 Physics Solutions Chapter 2 Electrostatic Potential and Capacitance


NCERT Exemplar Solutions Class 12 Physics Chapter 2 will assist you in mastering these concepts by providing clear step-by-step solutions to the questions on electric potential, work and electric fields, properties of equipotential surfaces, and capacitor behavior. Such solutions are particularly handy since they have a lot of varieties of questions e.g. MCQs, short answers, long answers as well as very long answers, as is the case in competitive exams or board papers. As you gear up to take CBSE exams, JEE or NEET, in these exemplar solutions you will learn ways to solve problems and understand the most basic concepts of physics in a practical manner by applying logic.

Also check - NCERT Solutions for Class 12 Physics

NCERT Exemplar Class 11 Physics Solutions Chapter 2: MCQI

Question:2.1

A capacitor of $4\mu F$ is connected as shown in the circuit. The internal resistance of the battery is $0.5\Omega$. The amount of charge on the capacitor plates will be

$a) 0$
$b) 4\mu C$
$c) 16\; \mu C$
$d) 8\; \mu C$

Answer:

The answer is the option (d) $8\mu C$
Current through the $2\Omega$ resistance considering internal resistance of the battery $1\Omega$,
$I=\frac{2.5V}{\left ( 2\Omega +0.5\Omega \right )}=1A$
The voltage across the internal resistance of the battery
$=\left ( 0.5\Omega \right )\left ( 1A \right )=0.5V$
The voltage across the $4\mu F$ capacitor
$2.5V-0.5V=2V$
Therefore, charge on the capacitor plates
$Q=CV=\left ( 4\mu F \right )\left ( 2V \right )=8\mu C$

Question:2.2

A positively charged particle is released from rest in a uniform electric field. The electric potential energy of the charge
a) remains a constant because the electric field is uniform
b) increases because the charge moves along the electric field
c) decreases because the charge moves along the electric field
d) decreases because the charge moves opposite to the electric field

Answer:

The answer is the option (c)

The direction of electric field is always perpendicular to one equipotential surface maintained at high electrostatic potential to other equipotential surface maintained at low electrostatic potential. The positively charged particle experiences electrostatic force along the direction of electric field i.e., from high electrostatic potential to low electrostatic potential. Thus, the work is done by the electric field on the positive charge, hence electrostatic potential energy of the positive charge decreases.

Question:2.3

Figure shows some equipotential lines distributed in space. A charged object is moved from point A to point B.

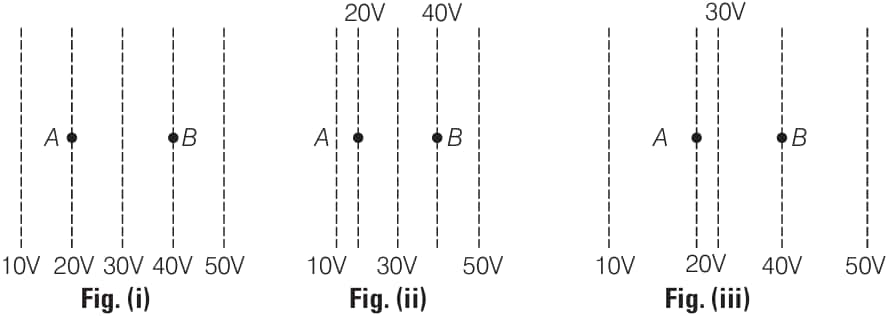
a) the work is done in fig (ii) is the least
b) the work is done in fig (i) is the greatest
c) the work is done in fig (iii) is greater than fig (ii) but equal to that in fig (i)
d) the work done is the same in fig (i), fig (ii), and fig (iii)

Answer:

The answer is the option (d)

The work done by a electrostatic force is given by $W_{12}=q\left(V_2-V_1\right)$. Here initial and final potentials are same in all three cases and same charge is moved, so work done is same in all three cases.

Question:2.4

The electrostatic potential on the surface of a charged conducting sphere is 100V. Two statements are made in this regard:
S1: At any point inside the sphere, the electric intensity is zero
S2: At any point inside the sphere, the electrostatic potential is 100V
Which of the following is a correct statement?
a) S1 and S2, both are false
b) S1 is true, S2 is false
c) S1 and S2, both are true but each of the statements is independent
d) S1 and S2, both are true and S1 is the cause of S2

Answer:

The answer is the option (d) S1 and S2, both are true, and S1 is the cause of S2

In this problem, the electric field intensity $E$ and electric potential $V$ are related as

$
E=-\frac{d V}{d r}
$
Electric field intensity $E=0$ suggest that $\frac{d V}{d r}=0$
This imply that $V=$ constant.
Thus, $E=0$ inside the charged conducting sphere causes, the same electrostatic potential 100 V at any point inside the sphere.

Question:2/5

Equipotential at a great distance from a collection of charges whose total sum is not zero are approximately
a) Ellipsoids
b) Spheres
c) Paraboloids
d) planes

Answer:

The correct answer is (b) spheres

In this problem, the collection of charges, whose total sum is not zero, with regard to great distance can be considered as a point charge. The equipotentials due to point charge are spherical in shape as electric potential due to point charge $q$ is given by

$
V=k \frac{q}{r}
$
This suggest that electric potentials due to point charge is same for all equidistant points. The locus of these equidistant points, which are at same potential, form spherical surface.

Question:2.6

A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness $d_{1}$ and dielectric constant $K_{1}$ and the other has thickness $d_{2}$ and dielectric constant $K_{2}$ as shown in the figure. This arrangement can be thought of as a dielectric slab of thickness $d=d_{1}+d_{2}$ and effective dielectric constant K. The K is

$a) \frac{2K_{1}K_{2}}{\left ( K_{1}+K_{2} \right )}$
$b) \frac{K_{1}d_{1}+K_{2}d_{2}}{\left ( d_{1}+d_{2} \right )}$
$c) \frac{\left ( K_{1}d_{1}+K_{2}d_{2} \right )}{\left ( K_{1}+K_{2} \right )}$
$d)\frac{K_{1}K_{2}\left ( d_{1}+d_{2} \right )}{\left ( K_{1}d_{1}+K_{2}d_{2} \right )}$

Answer:

The answer is the option (d)
${{C}_{eq}}=\dfrac{{{K}_{1}}{{K}_{2}}{{\varepsilon }_{0}}A}{{{K}_{1}}{{d}_{2}}+{{K}_{2}}{{d}_{1}}}.............(1)$
$C=\dfrac{K{{\varepsilon }_{0}}A}{{{d}_{1}}+{{d}_{2}}}.........(2)$
From (1) and (2)
$\dfrac{{{K}_{1}}{{K}_{2}}{{\varepsilon }_{0}}A}{{{K}_{1}}{{d}_{2}}+{{K}_{2}}{{d}_{1}}}=\dfrac{K{{\varepsilon }_{0}}A}{{{d}_{1}}+{{d}_{2}}}$
$K=\frac{K_{1}K_{2}\left ( d_{1}+d_{2} \right )}{\left ( K_{1}d_{1}+K_{2}d_{2} \right )}$

NCERT Exemplar Class 11 Physics Solutions Chapter 2: MCQII

Question:2.7

Consider a uniform electric field in the $\hat{z}$ direction. The potential is a constant
a) in all space
b) on the x-y plane for a given z
c) for any y for a given z
d) for any x for a given z

Answer:

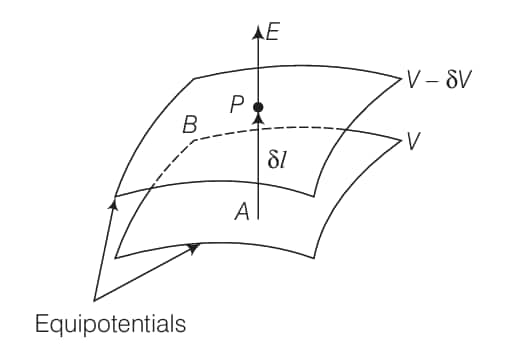
Here, the figure electric field is always remain in the direction in which the potential decreases steepest. Its magnitude is given by the change in the magnitude of potential per unit displacement normal to the equipotential surface at the point.
The electric field in z-direction suggest that equipotential surfaces are in $x-y$ plane. Therefore the potential is a constant for any $x$ for a given $z$, for any $y$ for a given $z$ and on the $x-y$ plane for a given $z$.

The answer are the options (b) on the x-y plane for a given z; (c) for any y for a given z; and (d) for any x for a given z.

Question:2.8

Equipotential surfaces
a) will always be equally spaced
b) are closer in regions of large electric fields compared to regions of lower electric fields
c) will be more crowded near regions of large charge densities
d) will be more crowded near sharp edges of a conductor

Answer:

The electric field intensity $E$ is inversely proportional to the separation between equipotential surfaces. So, equipotential surfaces are closer in regions of large electric fields.
Since, the electric field intensities is large near sharp edges of charged conductor and near regions of large charge densities. Therefore, equipotential surfaces are closer at such places.

The answer are the options,
b) are closer in regions of large electric fields compared to regions of lower electric fields
c) will be more crowded near sharp edges of a conductor
d) will be more crowded near regions of large charge densities

Question:2.9

The work done to move a charge along an equipotential from A to B
a) is zero
b) cannot be defined as $-\int_{A}^{B}E.dl$
c) must be defined as $-\int_{A}^{B}E.dl$
d) can have a non-zero value

Answer:

Work done in displacing a charge particle is given by $W_{12}=q\left(V_2-V_1\right)$ and the line integral of electrical field from point 1 to 2 gives potential difference $V_2-V_1=-\int_1^2 E . d$ For equipotential surface, $V_2-V_1=0$ and $W=0$.

Note If displaced charged particle is $+1 C$, then and only then option (b) is correct.

Question:2.10

In a region of constant potential

(a) the electric field is uniform
(b) the electric field is zero
(c) there can be no charge inside the region.
(d) the electric field shall necessarily change if a charge is placed outside the region.

Answer:

The electric field intensity $E$ and electric potential $V$ are related as $E=0$ and for $V=$ constant, $\frac{d V}{d r}=0$
This implies that electric field intensity $E=0$.

The correct answers are the options,
c) in the inside region there can be no charge
d) zero electric field will be there

Question:2.11

In the circuit shown in the figure, initially key $K_{1}$ is closed and $K_{2}$ is open. Then $K_{1}$ is opened and $K_{2}$ is closed. Then

a) charge on $C_{1}$ gets redistributed i.e, $V_{1}=V_{2}$
b) charge on $C_{1}$ gets redistributed i.e,$\left ( Q_{1}+Q_{2} \right )=Q$
c) charge on $C_{1}$ gets redistributed such that $Q_{1}=Q_{2}$
d) charge on $C_{1}$ gets redistributed such that $C_{1}V_{1}+C_{2}V_{2}=C_{1}E$

Answer:

The charge stored by capacitor $C_1$ gets redistributed between $C_1$ and $C_2$ till their potentials become same i.e., $V_2=V_1$. By law of conservation of charge, the charge stored in capacitor $C_1$ when key $K_1$ is closed and key $K_2$ is open is equal to sum of charges on capacitors $C_1$ and $C_2$ when $K_1$ is opened and $K_2$ is closed i.e.,

$
Q_1^{\prime}+Q_2^{\prime}=Q
$

The answers are the options,
a) charge on $C_{1}$ gets redistributed such that $V_{1}=V_{2}$
d) charge on $C_{1}$ gets redistributed such that $\left ( Q_{1}+Q_{2} \right )=Q$

Question: 2.12

If a conductor has a potential $V\neq 0$ and there are no charges anywhere else outside, then
a) the charges must on the surface or inside itself
b) no charge will be in the body of the conductor
c) the charges must be only on the surface
d) the charges must be inside the surface

Answer:

The charge resides on the outer surface of a closed charged conductor.

The answer are the options,
a) the charges must on the surface or inside itself
b) no charge will be in the body of the conductor

Question:2.13

A parallel plate capacitor is connected to a battery as shown in the figure. Consider two situations:
A: Key K is kept closed and plates of capacitors are moved apart using the insulating handle
B: Key K is opened, and plates of capacitors are moved apart using the insulating handle
Choose the correct options

(a) In A : Q remains same but C changes.
(b) In B : V remains same but C changes.
(c) In A : V remains same and hence Q changes.
(d) In B : Q remains same and hence V changes.

Answer:

Case A When key $K$ is kept closed and plates of capacitors are moved apart using insulating handle, the separation between two plates increases which in turn decreases its capacitance $\left(C=\frac{K \varepsilon_0 A}{d}\right)$ and hence, the charge stored decreases as $Q=C V$ ( potential continue to be the same as capacitor is still connected with cell).
Case B When key $K$ is opened and plates of capacitors are moved apart using insulating handle, charge stored by disconnected charged capacitor remains conserved and with the decreases of capacitance, potential difference $V$ increases as $V=Q / C$.

The answer is the options (a) and (d)

NCERT Exemplar Class 11 Physics Solutions Chapter 2: Very Short Answer

Question:2.14

Consider two conducting spheres of radius $R_{1}$ and $R_{2}$ with $R_{1} > R_{2}$. If the two are at the same potential, the larger sphere has more charge than the smaller sphere. State whether the charge density of the smaller sphere is more or less than that of the larger one.

Answer:

Here, $\sigma _{1}R_{1}=\sigma _{2}R_{2}$
Hence, $\frac{\sigma _{1}}{\sigma _{2}}=\frac{R_{2}}{R_{1}}$
If we consider $R_{2}>R_{1}$, therefore, $\sigma _{1}>\sigma _{2}$
Therefore, it is clear from the above statement that the charge density of the smaller sphere is greater than the charge density of the larger sphere.

Question:2.15

Do free electrons travel to a region of higher potential or lower potential?

Answer:

We know that the charged particle in the electric field has a force, that can be expressed as $F=qE$
Here, the direction of the electrostatic force experienced by the free electrons is exactly in the opposite direction of the electric field. The electrons travel from a lower potential region to a higher potential because the direction of the electric field is higher than the potential.

Question:2.16

Can there be a potential difference between two adjacent conductors carrying the same charge?

Answer:

Yes, it is possible and there may be a potential difference between two same charges carrying adjacent conductors. This is because the sizes of the conductors might be different

Question:2.17

Can the potential function have a maximum or minimum in free space?

Answer:

Because the atmosphere around the conductor that prevents the electric discharge is absent, therefore, the potential function cannot be maximum or minimum in free space.

Question: 2.18

A test charge q is made to move in the electric field of a point charge Q along two different closed paths. The first path has sections along and perpendicular to lines of the electric field, the second path is a rectangular loop of the same area as the first loop. How does the work done compare in the two cases?

Answer:
Here we can observe that the work done in both of the cases is zero. The work done due to the electric force on the charge is in the closed-loop and the value of it is equal to zero.

Recommended eBooks

Related eBooks & Sample Papers

NCERT Exemplar Class 11 Physics Solutions Chapter 2: Short Answer

Question:2.19

Prove that a closed equipotential surface with no charge within itself must enclose an equipotential volume.

Answer:

Let's assume contradicting statement that the potential is not same inside the closed equipotential surface. Let the potential just inside the surface is different to that of the surface causing in a potential gradient $\left(\frac{d V}{d r}\right)$. Consequently electric field comes into existence, which is given by as $E=-\frac{d V}{d r}$.
Consequently field lines pointing inwards or outwards from the surface. These lines cannot be again on the surface, as the surface is equipotential. It is possible only when the other end of the field lines are originated from the charges inside.
This contradict the original assumption. Hence, the entire volume inside must be equipotential.

Question:2.20

A capacitor has some dielectric between its plates, and the capacitor is connected to a DC source. The battery is now disconnected and then the dielectric is removed. State whether the capacitance, the energy stored in it, electric field, the charge stored, and the voltage will increase, decrease, or remain constant.

Answer:

Quantity
Battery is removed
Battery remains connected
Capacity
$C'=KC$
$C'=KC$
Charge
$Q'=Q$
$Q'=KQ$
Potential
$V'=\frac{V}{K}$
$V'V$
Intensity
$E'=\frac{E}{K}$
$E'=E$
Energy
$U'=\frac{U}{K}$
$U'=UK$

Question:2.21

Prove that, if an insulated, uncharged conductor is placed near a charged conductor and no other conductors are present, the uncharged body must be intermediate in potential between that of the charged body and that of infinity.

Answer:

The electric potential will decrease in the direction of the electric field. The potential
$E=-\frac{dV}{dr}$
The electric potential will also decrease again when the path from the charged conductor is taken to the uncharged conductor in the direction of the electric field.
This process will continue when another uncharged conductor is considered to the infinity lowering the potential even further.
As a result, the uncharged body is at intermediate potential and the charged body is at infinity potential.

Question:2.22

Calculate the potential energy of a point charge $-q$ placed along the axis due to charge $+Q$ uniformly distributed along a ring of radius R. Sketch PE as a function of axial distance z from the center of the ring. Looking at the graph, can you see what would happen if $-q$ is displaced slightly from the center of the ring?

Answer:
The potential energy of a point charge q is U and this point is placed at potential V, $U=qV$
A negatively charged particle is placed at the axis of the ring with charge Q
Let a be the radius of the ring
The electric potential at the axial distance is given as
$V=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{\sqrt{z^{2}+a^{2}}}$
The potential energy, U is given as
$U=\frac{1}{4\pi \epsilon _{0}}\frac{Qq}{\sqrt{1+\left ( \frac{z}{a} \right )^{2}}}$
When z=infinity, U=0.
When z=0, U is given as
$U=\frac{1}{4\pi \epsilon _{0}}\frac{Qq}{a}$

Question:2.23

Calculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.

Answer:


Here, in the above image, point P is perpendicular to O and is at a distance of z from point O, which is the centre of the ring.
The charge dq is at a distance z from the point P.
Therefore, V can be written as:
$V=\frac{1}{4\pi \epsilon _{0}}\int \frac{dq}{r}=\frac{1}{4\pi \epsilon _{0}}\int \frac{dq}{\sqrt{z^{2}+a^{2}}}$
Therefore, the net potential will be :
$V=\frac{1}{4\pi \epsilon _{0}}\frac{Q}{\sqrt{z^{2}+a^{2}}}$

NCERT Exemplar Class 11 Physics Solutions Chapter 2: Long Answer

Question:2.24

Find the equation of the equipotential for an infinite cylinder of radius $r_{0}$, carrying charge of linear density $\lambda$.

Answer:

Let the field lines must be radically outward. Draw a cylindrical Gaussian surface of radius $r$ and length $l$. Then, applying Gauss' theorem

$
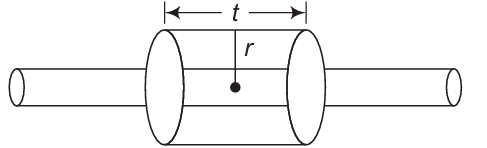
\begin{aligned}
& \int \mathrm{E} . \mathrm{dS}=\frac{1}{\varepsilon_0} \lambda l \\
& E_r 2 \pi r l=\frac{1}{\varepsilon_0} \lambda l \Rightarrow E_r=\frac{\lambda}{2 \pi \varepsilon_0 r}
\end{aligned}
$


Hence, if $r_0$ is the radius,

$
V(r)-V\left(r_0\right)=-\int_{r_0}^r \mathrm{E} \cdot \mathrm{dl}=\frac{\lambda}{2 \pi \varepsilon_0} \ln \frac{r_0}{r}
$


Since,

$
\int_{r_0}^r \frac{\lambda}{2 \pi \varepsilon_0 r} d r=\frac{\lambda}{2 \pi \varepsilon_0} \int_{r_0}^r \frac{1}{r} d r=\frac{\lambda}{2 \pi \varepsilon_0} \ln \frac{r}{r_0}
$


For a given $V$,

$
\Rightarrow \quad \begin{aligned}
r & =r_0 e^{-2 \pi \varepsilon_0 V r_0 / \lambda} e+2 \pi \varepsilon_0 V(r) / \lambda \\
r & =r_0 e^{-2 \pi \varepsilon_0\left[V_{(r)}-V_{\left(r_0\right)}\right] \lambda}
\end{aligned}
$

Question:2.25

Two-point charges of magnitude $\text {+q and -q}$ are placed at $\left ( \frac{-d}{2},0,0 \right )$ and $\left ( \frac{d}{2},0,0 \right )$ respectively. Find the equation of the equipotential surface where the potential is zero.

Answer:


Here, the potential due to charges at the point P is
$V_{p}=\frac{1}{4\pi\varepsilon _{0}}\frac{q}{r_{1}}+\frac{1}{4\pi\varepsilon _{0}}\frac{(-q)}{r_{2}}$
The net electric potential at this point is zero,
Therefore, $r_{1}=r_{2}$
We know that
$r_{1}=\sqrt{\left ( \frac{x+d}{2} \right )^{2}+h^{2}}$
$r_{2}=\sqrt{\left ( \frac{x-d}{2} \right )^{2}+h^{2}}$
Solving the two equations, we the required equation in-plane x = 0 which is a y-z plane.

Question:2.26

A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (U) as $\varepsilon =\alpha U$ where $\alpha =2V-1.$ A similar capacitor with no dielectric is charged to $U_{0}=78 V$. It is then connected to the uncharged capacitor with the dielectric. Find the final voltage on the capacitors.

Answer:

Here, the capacitors are connected in parallel. Therefore, the voltage across the capacitors is the same. Let us assume the final voltage is U. Here, C is the capacitance of the capacitor without the dielectric. At this point, the charge is $Q_{1}=CU$
If the initial charge is $Q_{0}$ given by $Q_{0}=CU_{0}$
The conversion of charges is
$Q_{1}=Q_{1}+Q_{2}$
$CU_{0}=CU+\alpha CU_{2}$
$\alpha U_{2}+U-U_{o}=0$
Solving the equation, we get $U=6V$

Question:2.27

A capacitor is made of two circular plates of radius R each, separated by a distance $d < < R$. The capacitor is connected to a constant voltage. A thin conducting disc of radius $r < < R$ and thickness $t < < r$ is placed at the center of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.

Answer:

Assuming initially the disc is in touch with the bottom plate, so the entire plate is a equipotential.

The electric field on the disc, when potential difference $V$ is applied across it, given by

$
E=\frac{V}{d}
$


Let charge $q$ ' is transferred to the disc during the process,
Therefore by Gauss' theorem,

$
\therefore \quad q^{\prime}=-\varepsilon_0 \frac{V}{d} \pi r^2
$


Since, Gauss theorem states that

$
\begin{aligned}
\phi & =\frac{q}{\varepsilon_0} \text { or } q=\frac{\varepsilon_0}{\phi} \\
& =\varepsilon E A=\frac{\varepsilon_0 V}{d} A
\end{aligned}
$


The force acting on the disc is

$
-\frac{V}{d} \times q^{\prime}=\varepsilon_0 \frac{V^2}{d^2} \pi r^2
$


If the disc is to be lifted, then

$
\varepsilon_0 \frac{V^2}{d^2} \pi r^2=m g \Rightarrow V=\sqrt{\frac{m g d^2}{\pi \varepsilon_0 r^2}}
$


This is the required expression.

Question:2.28

In a quark model of elementary particles, a neutron is made of one up quarks and two down quarks. Assume that they have a triangle configuration with a side length of the order of $10^{-15}$ m. Calculate the electrostatic potential energy of the neutron and compare it with its mass 939 MeV.

Answer:

This system is made up of three charges. The potential energy of the system is equal to the algebraic sum of PE of each pair. So,

$
\begin{aligned}
U & =\frac{1}{4 \pi \varepsilon_0}\left\{\frac{q_d q_d}{r}-\frac{q_u q_d}{r}-\frac{q_u q_d}{r}\right\} \\
& =\frac{9 \times 10^9}{10^{-15}}\left(1.6 \times 10^{-19}\right)^2\left[\left\{(1 / 3)^2-(2 / 3)(1 / 3)-(2 / 3)(1 / 3)\right\}\right] \\
& =2.304 \times 0^{-13}\left\{\frac{1}{9}-\frac{4}{9}\right\}=-7.68 \times 10^{-14} \mathrm{~J} \\
& =4.8 \times 10^5 \mathrm{eV}=0.48 \mathrm{meV}=5.11 \times 10^{-4}\left(m_n c^2\right)
\end{aligned}
$

Question:2.29

Two metal spheres, one of radius R and the other of radius 2R, both have the same surface charge density $\sigma$. They are brought in contact and separated. What will be the new surface charge densities on them?

Answer:

Let us say, the charge stored on the first and second metal spheres before contact is $Q_{1}$ and $Q_{2}$ respectively.
Therefore,
$Q_{1}=\sigma .4\pi R^2$
$Q_{2}=\sigma .4\pi (2R)^2=4\; Q_{1}$
Again assume, the charge stored on the first and second metal spheres are $Q{_{1}}^{'}$ and $Q{_{2}}^{'}$ respectively.
Therefore,
$\left ( Q{_{1}}^{'}+Q{_{2}}^{'} \right )=\left ( Q{_{1}}+Q{_{2}} \right )=5\; Q_{1}$
When the metal spheres are in contact, the following is the potentials acquired by them
$Q{_{1}}^{'} = \frac{Q{_{2}}^{'}}{2}$
By solving the above equations, we get,
$\sigma_1=5\frac{\sigma }{3}$
$\sigma_2=5\frac{\sigma }{6}$

Question:2.30

In the circuit shown in the figure, initially, $K_{1}$ is closed and $K_{2}$ is open. What are the charges on each capacitor? Then $K_{1}$ was opened and $K_{2}$ was closed. What will be the charge on each capacitor now?

Answer:


When key $K_{1}$ is closed and key $K_{2}$ is open, then capacitors $C_{1}$ and $C_{2}$ are connected in series with the battery.
Therefore, the charge stored in the capacitors $C_{1}$ and $C_{2}$ will be same as $Q_{1}=Q_{2}$
Therefore, $Q_{1}=Q_{2}=q=\left ( \frac{C_{1}}{\left ( C_{1}+C_{2} \right )} \right )E=18\mu C$

Assuming only capacitors $C_{2}$ and $C_{3}$ are placed in parallel,
$C_{2}V'+ C_{3}V'=Q_{2}$
$V'=\frac{Q_{2}}{C_{2}+C_{3}}=3V$
Therefore,
$Q{_{2}}^{'}=3CV'=9\; \mu C$
$Q{_{3}}=3CV'= 9\mu C$
$Q{_{1}}^{'}=18\; \mu C$

Question:2.31

Calculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface.

Answer:


In the above figure, we can see that the disc is divided into several charged rings. Let P be the point on the axis of the disc at a distance x from the centre of the disc.
The radius of the ring is r and the width is dr. dq is the charge on the ring which is given as
$dq=\sigma dA=\sigma 2\pi rdr$
The potential is given as
$dV=\frac{1}{4\pi\varepsilon _{0}}\frac{dq}{\sqrt{r^{2}+x^{2}}}=\frac{1}{4\pi \varepsilon _{0}}\frac{\left ( \sigma 2\pi rdr \right )}{\sqrt{r^{2}+x^{2}}}$
The total potential at P is given as
$\frac{Q}{2\pi \varepsilon _{0}R^2}\left ( \sqrt{R_{2}+x_{2}-x} \right )$

Question:2.32

Two charges $q_{1}$ and $q_{2}$ are placed at $(0, 0, d)$ and $(0, 0, -d)$ respectively. Find the locus of points where the potential is zero.

Answer:


We know that the potential at point P is $V=\sum Vi$
Where $Vi=\frac{qi}{4\pi \varepsilon _{0}}$, ri is the magnitude of the position vector P
$V=\frac{1}{4 \pi \varepsilon _{0}}\sum \frac{qi}{rpi}$
When the (x,y,z) plane is considered, the two charges lie on the z-axis and are separated by 2d. The potential is given as
$\frac{q_{1}}{\sqrt{x^{2}+y^{2}+\left ( z-d \right )^{2}}}+\frac{q_{2}}{\sqrt{x^{2}+y^{2}+\left ( z+d \right )^{2}}}=0$
Squaring the equation, we get
$x^{2}+y^{2}+z^{2}+\left [ \left ( \frac{q_{1}^2+q_2^2}{q_{1}^2-q_2^2} \right )^2 \right ]\left ( 2zd \right )+d^2=0$
The Centre of the sphere is
$\left ( 0,0,-d\left [ \frac{q_{1}^{2}+q_{2}^{2}}{q_{1}^{2}-q_{2}^{2}} \right ] \right )$
And radius is
$r=\frac{2q_{1}q_{2}d}{q_{1}^{2}-q_{2}^{2}}$

Question:2.33

Two charges $-q$ each are separated by distance 2d. A third charge $+q$ is kept at midpoint O. Find potential energy of $+q$ as a function of small distance x from O due to $-q$ charges. Sketch PE versus x and convince yourself that the charge at O is in an unstable equilibrium.

Answer:


In the above figure, $+q$ charge is at a point away from O towards $\left ( -d,0 \right )$.
This can be written as
$U=q\left ( V_{1}+V_{2} \right )=q\frac{1}{4\pi\; \varepsilon _{0}}[\frac{-q}{\left ( d-x \right )}+\frac{-q}{d+x}]$
$U=\frac{1}{2\pi\varepsilon _{0}}\frac{-q^{2}d}{d^{2}-x^{2}}$
At x=0;
$U=\frac{1}{2\pi\varepsilon _{0}}\frac{q^{2}}{d}$
If we differentiate both sides of the equation with respect to x, we get
$\frac{dU}{dx}>0,$ when $x<0$
and $\frac{dU}{dx}<0,$ when $x>0$
With the help of this two, we can assume that the charge on the particle to be
$F=\frac{-dU}{dx}$
Hence, $F=\frac{-dU}{dx}=0$
When
a) $\frac{d^2U}{dx^{2}}$ = positive, equilibrium is stable
b) $\frac{d^2U}{dx^{2}}$ = negative, equilibrium is unstable
c) $\frac{d^2U}{dx^{2}}=0$, equilibrium is neutral
Therefore, when
$x=0,\frac{d^2U}{dx^{2}}=\left ( \frac{-2dq2}{4\pi\varepsilon _{0}} \right )\left ( \frac{1}{d^{6}} \right )\left ( 2d^2 \right )<0$
Which shows that the system is an unstable equilibrium.

Main Topics of NCERT Exemplar Class 12 Physics Solutions Chapter 2

Aakash Repeater Courses

Take Aakash iACST and get instant scholarship on coaching programs.

Apply

NCERT Exemplar Class 12 Physics Solutions Chapter-Wise

Chapter 1 Electric Charges and Fields

Chapter 2 Electrostatic Potential and Capacitance

Chapter 3 Current Electricity

Chapter 4 Moving Charges and Magnetism

Chapter 5 Magnetism and Matter

Chapter 6 Electromagnetic Induction

Chapter 7 Alternating Current

Chapter 8 Electromagnetic Waves

Chapter 9 Ray Optics and Optical Instruments

Chapter 10 Wave Optics

Chapter 11 Dual Nature of Radiation and Matter

Chapter 12 Atoms

Chapter 13 Nuclei

Chapter 14 Semiconductor Electronics

Chapter 15 Communication Systems

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

NCERT Exemplar Class 12 Solutions

Check Class 12 Physics Chapter-wise Solutions

NCERT solutions for Class 12 Physics Chapter 1 Electric Charges and Fields
NCERT solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance
NCERT solutions for Class 12 Physics Chapter 3 Current Electricity
NCERT solutions for Class 12 Physics Chapter 4 Moving charges and magnetism
NCERT solutions for Class 12 Physics Chapter 5 Magnetism and Matter
NCERT solutions for Class 12 Physics Chapter 6 Electromagnetic Induction
NCERT solutions for Class 12 Physics Chapter 7 Alternating Current
NCERT solutions for Class 12 Physics Chapter 8 Electromagnetic Waves
NCERT solutions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
NCERT solutions for Class 12 Physics Chapter 10 Wave Optics
NCERT solutions for Class 12 Physics Chapter 11 Dual nature of radiation and matter
NCERT solutions for Class 12 Physics Chapter 12 Atoms
NCERT solutions for Class 12 Physics Chapter 13 Nuclei
NCERT Solutions for Class 12 Physics Chapter 14 Semiconductor Electronics Materials Devices And Simple Circuit

Also, Read NCERT Solution subject-wise

Must read NCERT Notes subject-wise

Also, Check NCERT Books and NCERT Syllabus

Frequently Asked Questions (FAQs)

Q: How are the questions solved in NCERT exemplar Class 12 Physics solutions chapter 2?
A:

All these questions given in the chapter are solved exhaustively, with proper explanation, steps, diagrams and conclusion.

Q: How many questions are solved?
A:

  In all 33 questions from main exercise is solved in detail in the NCERT exemplar Class 12 Physics solutions chapter 2 Electrostatic Potential and Capacitance

Q: Who has solved these questions?
A:

Our very own highly experienced teachers of physics have solved these questions as per the CBSE pattern

Articles
Related Stories
|
Next
Previous
Next
Upcoming School Exams
Uttar Pradesh Board 12th Examination
Ongoing Dates
UP Board 12th Others

7 Sep'25 - 11 Sep'25 (Online)

Uttar Pradesh Board 10th examination
Ongoing Dates
UP Board 10th Others

7 Sep'25 - 11 Sep'25 (Online)

Certifications By Top Providers
People Management with Impact
Via Indian Institute of Management Bangalore
Forensic Science DNA Analysis
Via University of Cambridge, Cambridge
Basic 3D Animation using Blender
Via Indian Institute of Technology Bombay
Consumer Behaviour
Via Indian Institute of Management Bangalore
Certificate Course Animation Technology
Via Manipal Institute of Communication, Manipal
Edx
 1078 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 281 courses
Explore Top Universities Across Globe
University of Essex, Colchester
Wivenhoe Park Colchester CO4 3SQ
University College London, London
Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Nottingham, Nottingham
University Park, Nottingham NG7 2RD
Bristol Baptist College, Bristol
The Promenade, Clifton Down, Bristol BS8 3NJ

Questions related to CBSE Class 12th

On Question asked by student community

Have a question related to CBSE Class 12th ?
how may marks should i get in my 12th board exams to get fee concesion in sastra university

Hello Aspirant,

SASTRA University commonly provides concessions and scholarships based on merit in class 12 board exams and JEE Main purposes with regard to board merit you need above 95% in PCM (or on aggregate) to get bigger concessions, usually if you scored 90% and above you may get partial concessions. I suppose the exact cut offs may change yearly on application rates too.

Read Complete Answer
G
gopi
4 Sep'25
Which course is best for computer science students after 12th standard

Hello,

After 12th, if you are interested in computer science, the best courses are:

  • B.Tech in Computer Science Engineering (CSE) – most popular choice.

  • BCA (Bachelor of Computer Applications) – good for software and IT jobs.

  • B.Sc. Computer Science / IT – good for higher studies and research.

  • B.Tech in Information Technology (IT) – focuses on IT and networking.

All these courses have good career scope. Choose based on your interest in coding, software, hardware, or IT field.

Hope it helps !

Read Complete Answer
P
Prachi Kumari
4 Sep'25
I am a CBSE class 12 private candidate will my maksheet of CBSE supplement exam will be delivered on main exam form address for supplementary exam form address ,my both addresses are different please tell

Hello Vanshika,

CBSE generally forwards the marksheet for the supplementary exam to the correspondence address as identified in the supplementary exam application form. It is not sent to the address indicated in the main exam form. Addresses that differ will use the supplementary exam address.

Read Complete Answer
G
gopi
3 Sep'25
I gave my 12th exam this year in which I got less marks. Then I gave improvement exam in which also I could not score full marks. So can I become a private candidate and appear for the exam again next year or not?

Hello

Yes, if you’re not satisfied with your marks even after the improvement exam, many education boards allow you to reappear as a private candidate next year to improve your scores. This means you can register independently, study at your own pace, and take the exams without attending regular classes. It’s a good option to improve your results and open up more opportunities for higher studies or careers. Just make sure to check the specific rules and deadlines of your education board so you don’t miss the registration window. Keep your focus, and you will do better next time.

Read Complete Answer
S
SEJAL JAIN
20 Aug'25
i gave improvement 2025 as the roll no is different from my previous year marksheet so will i get new migration certificate

Hello Aspirant,

Yes, in the case that you appeared for the 2025 improvement exam and your roll number is different from what was on the previous year’s marksheet, the board will usually release a new migration certificate. This is because the migration certificate will reflect the most recent exam details, roll number and passing year. You can apply to get it from your board using the process prescribed by them either online or through your school/college.

Read Complete Answer
G
gopi
12 Aug'25
View all

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read Complete Answer

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read Complete Answer

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read Complete Answer

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read Complete Answer

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read Complete Answer

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read Complete Answer

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read Complete Answer

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read Complete Answer

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read Complete Answer

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read Complete Answer

Study Resources, Applications and Opportunities

Aakash Repeater Courses
Apply

Take Aakash iACST and get instant scholarship on coaching programs.

NEET Most scoring concepts
Get now

This ebook serves as a valuable study guide for NEET 2025 exam.

NEET Previous 10 Year Questions
Get now

This e-book offers NEET PYQ and serves as an indispensable NEET study material.

JEE Main Important Physics formulas
Get now

As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Get now

As per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

JEE Main high scoring chapters and topics
Get now

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

View all Application Forms

CBSE Class 12th Notifications

Latest updates

Never miss an CBSE Class 12th update

Get timely CBSE Class 12th updates directly to your inbox. Stay informed!