NCERT Exemplar Class 12 Physics Solutions Chapter 13 Nuclei

Question:13.2

The gravitational force between an H-atom and another particle of mass m will be given by Newton’s law: F = G M.m/r², where r is in km and
(a) M = m proton + m electron
(b) M = m proton + m electron - (|V |/c²) (where |V| = magnitude of the potential energy of the electron in the H-atom)
(c) M is not related to the mass of the hydrogen atom
(d) M = m proton + m electron – (B/c²) (where, B = 13.6 eV)

Answer:

The correct answer is option (d)

Given,

$
\begin{aligned}
F & =\frac{G M m}{r^2} \\
M & =\text { effective mass of hydrogen atom } \\
& =\text { mass of electron }+ \text { mass of proton }-\frac{B^2}{C}
\end{aligned}
$

where $B$ is $B E$ of hydrogen atom $=13.6 \mathrm{eV}$.

Question:13.3

When a nucleus in an atom undergoes radioactive decay, the electronic energy levels of the atom
(a) change for $\alpha$-radioactivity but not for others
(b) change for $\beta$-radioactivity but not for others
(c) do not change for any type of radioactivity
(d) change for α and $\beta$ radioactivity but not for γ-radioactivity

Answer:

The correct answer is option (d), change for $\alpha$ and $\beta$ radioactivity but not for γ-radioactivity

$\alpha-\beta$ particle carries one unit of negative charge, an $\alpha$-particle carries 2units of positive charge, and $\gamma$ (particle) carries no charge; therefore, electronic energy levels of the atom charges for $\alpha$ and $\beta$ decay, but not for $\gamma$-decay.

Question:13.4

M_x and M_y denote the atomic masses of the parent and the daughter nuclei respectively in a radioactive decay. The Q-value for a - decay is Q₁ and that for a + decay is Q₂. If m_e denotes the mass of an electron, then which of the following statements is correct?
(a) Q₁ = (M_x – M_y)c² and Q₂ = (M_x – M_y )c²
(b) Q₁ = (M_x – M_y)c² and Q₂ = (M_x – M_y – 2m_e )c²
(c) Q₁ = (M_x – M_y– 2me)c² and Q₂ = (M_x – M_y +2m_e )c²
(d) Q₁ = (M_x – M_y + 2me )c² and Q₂ = (M_x – M_y +2m_e )c²

Answer:

The correct answer is the option (b) Q₁ = (M_x – M_y) c² and Q₂ = (M_x – M_y – 2m_e )c²

Let the nucleus is ${ }_z X^A \cdot \beta^{+}$decay is represented as

$
\begin{aligned}
&{ }_z X^A \rightarrow_{z-1} Y^A+{ }_{+1} e^0+v+Q_2 \\
& Q_2=\left[m_n\left({ }_z X^A\right)-m_n\left({ }_{z-1} Y^A\right)-m_e\right] c^2 \\
&=\left[m_n\left({ }_z X^A\right)+z m_e-m_n\left({ }_{z-1} Y^A\right)-(z-1) m_e-2 m_e\right] c^2 \\
&=\left[m\left({ }_z X^A\right)-m\left({ }_{z-1} Y^A\right)-2 m_e\right] c^2 \\
&=\left(M_x-M_y-2 m_e\right) c^2
\end{aligned}
$

$\beta^{-}$decay is represented as

$
\begin{aligned}
& { }_z X^A \rightarrow_{z+1} A^Y+{ }_{-1} e^0+\bar{v}+\alpha_1 \\
\alpha_1 & =\left[m_n\left({ }_z X^A\right)-m_n\left({ }_{z+1} Y^A\right)-m_e\right] c^2 \\
& =\left[m_n\left({ }_z X^A\right)+z m_e-m_n\left({ }_{z+1} Y^A\right)-(z+1) m e\right] c^2 \\
& =\left[m\left({ }_z X^A\right)-m\left({ }_{z-1} Y^A\right)\right] c^2 \\
& =\left(M_x-M_y\right) c^2
\end{aligned}
$

Question:13.5

Tritium is an isotope of hydrogen whose nucleus Triton contains 2 neutrons and 1 proton. Free neutrons decay into $p+\overline{\mathrm{e}}+\bar{v}$. If one of the neutrons in Triton decays, it would transform into $\mathrm{He}^3$ nucleus. This does not happen. This is because
(a) because free neutrons decay due to external perturbations which is absent in a triton nucleus
(b) the electron created in the beta decay process cannot remain in the nucleus
(c) both the neutrons in triton have to decay simultaneously resulting in a nucleus with 3 protons, which is not a He³ nucleus
(d) Triton energy is less than that of a He³ nucleus

Answer:

The correct answer is option (d) Triton energy is less than that of a He³ nucleus

Tritium $\left({ }_1 \mathrm{H}^3\right)$ contains 1 proton and 2 neutrons. A neutron decays as $n \longrightarrow p+\bar{e}+\bar{v}$, the nucleus may have 2 protons and one neutron, i.e., tritium will transform into $2 \mathrm{He}^3$ (2 protons and 1 neutron).
Triton energy is less than that of $2 \mathrm{He}^3$ nucleus, i.e., transformation is not allowed energetically.

Question:13.6

Heavy stable nuclei have more neutrons than protons. This is because of the fact that
(a) neutrons are heavier than protons
(b) electrostatic force between protons are repulsive
(c) neutrons decay into protons through beta decay
(d) nuclear forces between neutrons are weaker than that between protons

Answer:

The correct answer is option (b) electrostatic force between protons is repulsive

Stable heavy nuclei have more neutrons than protons. This is because the electrostatic force between protons is repulsive, which may reduce stability.

Question:13.7

In a nuclear reactor, moderators slow down the neutrons which come out in a fission process. The moderator used to have light nuclei. Heavy nuclei will not serve the purpose because
(a) they will break up
(b) elastic collision of neutrons with heavy nuclei will not slow them down
(c) the net weight of the reactor would be unbearably high
(d) substances with heavy nuclei do not occur in a liquid or gaseous state at room temperature

Answer:

The correct answer is option (b) elastic collision of neutrons with heavy nuclei will not slow them down

According to the question, the moderator used had light nuclei (like protons). When protons undergo a perfectly elastic collision with the neutron emitted, their velocities are exchanged, i.e., neutrons come to rest and protons move with the velocity of neutrons. Heavy nuclei will not serve the purpose because elastic collisions of neutrons with heavy nuclei will not slow them down.

Question:13.9

Samples of two radioactive nuclides A and B are taken. $\lambda$ _A and $\lambda$_B are the disintegration constants of A and B respectively. In which of the following cases, the two samples can simultaneously have the same decay rate at any time?
(a) Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λ_B < λ_A
(b) Initial rate of decay of A is twice the initial rate of decay of B and $\lambda$_A > $\lambda$_B
(c) Initial rate of decay of A is twice the initial rate of decay of B and $\lambda$_A = $\lambda$_B
(d) Initial rate of decay of B is twice the initial rate of decay of A and $\lambda$_A > $\lambda$_B

Answer:

The correct answers are the options,
(a) Initial rate of decay of B is the same as the rate of decay of A at t = 2h and λ_B < λ_A
(b) Initial rate of decay of A is twice the initial rate of decay of B, and λ_A > λ_B

The two samples of the two radioactive nuclides $A$ and $B$ can simultaneously have the same decay rate at any time if the initial rate of decay of $A$ is twice the initial rate of decay of $B$ and $\lambda_A>\lambda_B$. Also, when the initial rate of decay of $B$ is the same as the rate of decay of $A$ at $t=2$ and $\lambda_B<\lambda_A$.

Question:13.10

The variation of the decay rate of two radioactive samples A and B with time is shown in the figure. Which of the following statements are true?

(a) The decay constant of A is greater than that of B, hence A always decays faster than B
(b) The decay constant of B is greater than that of A but its decay rate is always smaller than that of A
(c) The decay constant of A is greater than that of B but it does not always decay faster than B
(d) The decay constant of B is smaller than that of A but still, its decay rate becomes equal to that of A at a later instant

Answer:

The correct answers are the options,
(c) The decay constant of A is greater than that of B, but it does not always decay faster than B
(d) The decay constant of B is smaller than that of A, but still, its decay rate becomes equal to that of A at a later instant

From the given figure, it is clear that the slope of curve $A$ is greater than that of curve $B$. So the rate of decay is faster for $A$ than that of $B$.

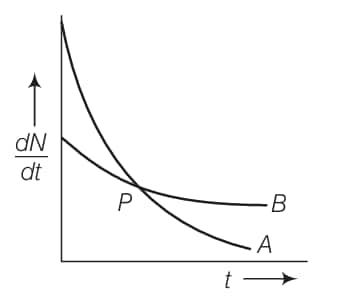
We know that $\left(\frac{d N}{d t}\right) \propto, \lambda$, at any instant of time, hence we can say that $\lambda_A>\lambda_B$. At point $P$ shown in the diagram, the two curves intersect.
Hence, at point $P$, the rate of decay for both $A$ and $B$ is the same.

Question:13.12

Draw a graph showing the variation of decay rate with the number of active nuclei.

Answer:

From the Rutherford and Soddy law, we get, the radioactive decay can be expressed as$-\frac{dn}{dt}=\lambda N$

Question:13.13

Which sample, A or B shown in the figure has shorter mean-life?

Answer:

$
\begin{aligned}
&\text { From the given figure, we can say that }\\
&\begin{aligned}
& \text { at } t=0,\left(\frac{d N}{d t}\right)_A=\left(\frac{d N}{d t}\right)_B \\
& \Rightarrow \quad\left(N_0\right)_A=\left(N_0\right)_B
\end{aligned}
\end{aligned}
$

Considering any instant $t$ by drawing a line perpendicular to the time axis, we find that $\left(\frac{d N}{d t}\right)_A>\left(\frac{d N}{d t}\right)_B$

$\begin{array}{lrl}\Rightarrow & \lambda_A N_A>\lambda_B N_B & \\ \because & N_A>N_B & \text { (rate of decay of } B \text { is slower) } \\ \therefore & \lambda_B>\lambda_A & \\ \Rightarrow & \tau_A>\tau_B & {\left[\because \text { Average life } \tau=\frac{1}{\lambda}\right]}\end{array}$

Question:13.14

Which one of the following cannot emit radiation and why? Excited nucleus, excited electron.

Answer:

An excited electron cannot emit radiation because the energy of electronic energy levels is in the range of eV and not MeV ( mega electron volt ).

Question:13.15

In pair annihilation, an electron and a positron destroy each other to produce gamma radiation. How is the momentum conserved?

Answer:

An electron and a positron destroy each other to produce gamma radiation in the case of pair annihilation. During this process, they used to go in opposite directions in order to conserve their momentum.

Question:13.17

Consider a radioactive nucleus A which decays to a stable nucleus C through the following sequence: A → B → C Here B is an intermediate nuclei which is also radioactive. Considering that there are N₀ atoms of A initially, plot the graph showing the variation of a number of atoms of A and B versus time.

Answer:

Here, in the above graph:
At t=0, N_A = N₀
N_A falls off exponentially with the increase in time.
As a result, the number of atoms of B increases, it will be maximum once and then decays to zero at $\mathrm{\infty }$

Question:13.18

A piece of wood from the ruins of an ancient building was found to have a ¹⁴C activity of 12 disintegrations per minute per gram of its carbon content. The ¹⁴C activity of the living wood is 16 disintegrations per minute per gram. How long ago did the tree, from which the wooden sample came, die? Given the half-life of ¹⁴C is 5760 years.

Answer:

As per the information given in the question, the ¹⁴C activity of a piece of wood from the ruins is R = 12 dis/min per gram
¹⁴C activity of a living wood = R_o = 16 dis/min per gram
The half-life of ¹⁴C = 5760 years

According to the radioactive decay law,

$
R=R_0 e^{-\lambda t} \text { or } \frac{R}{R_0}=e^{-\lambda t} \text { or } e^{\lambda t}=\frac{R_0}{R}
$
Taking the log on both sides

$\begin{array}{rlr}\lambda t \log _e e & =\log _e \frac{R_0}{R} \Rightarrow \lambda t=\left(\log _{10} \frac{16}{12}\right) \times 2.303 & \\ t & =\frac{2.303(\log 4-\log 3)}{\lambda} & \\ & =\frac{2.303(0.6020-4.771) \times 5760}{0.6931} & \left(\because \lambda=\frac{0.6931}{T_{1 / 2}}\right) \\ & =2391.20 \mathrm{yr} & \end{array}$

Question:13.19

Are the nucleons fundamental particles, or do they consist of still smaller parts? One way to find out is to probe a nucleon just as Rutherford probed an atom. What should be the kinetic energy of an electron for it to be able to probe a nucleon? Assume the diameter of a nucleon to be approximately 10^–15 m.

Answer:

We know that, $\lambda$ = h/p and kinetic energy = potential energy
E = hc/ $\lambda$
Kinetic energy of an electron
KE = PE = hc/ $\lambda$ = 10⁹ eV

Question:13.20

A nuclide 1 is said to be the mirror isobar of nuclide 2 if Z₁ =N₂ and Z₂ =N₁.
(a) What nuclide is a mirror isobar of ${ }_{11}^{23} \mathrm{Na}$?
(b) Which nuclide out of the two mirror isobars has greater binding energy and why?

Answer:

(a) According to the question, a nuclide 1 is said to be a mirror isobar of nuclide 2, if $Z_1=N_2$ and $Z_2=N_1$.

Now in ${ }_{11} \mathrm{Na}^{23}, Z_1=11, N_1=23-11=12$

$\therefore$ Mirror isobar of ${ }_{11} \mathrm{Na}^{23}$ is ${ }_{12}, \mathrm{Mg}^{23}$, for which $Z_2=12=N_1$ and $N_2=23-12=11=Z_1$

(b) As ${ }_{12}^{23} \mathrm{Mg}$ contains even number of protons (12) against ${ }_{11}^{23} \mathrm{Na}$ which has odd number of protons (11), therefore ${ }_{11}^{23} \mathrm{Mg}$ has greater binding energy than ${ }_{11} \mathrm{Na}^{23}$.

Question:13.22

Deuteron is a bound state of a neutron and a proton with a binding energy B = 2.2 MeV. A γ -ray of energy E is aimed at a deuteron nucleus to try to break it into a (neutron + proton) such that the n and p move in the direction of the incident γ-ray. If E = B, show that this cannot happen. Hence calculate how much bigger than B must E be for such a process to happen.
Answer:

Given the binding energy of a deuteron, $\mathrm{B}=2.2 \mathrm{MeV}$
Let kinetic energy and momentum of neutron and proton be $K_n, K_P$ and $p_n, p_p$ respectively.
From the conservation of energy,

$
E-B=K_n+K_p=\frac{p_n^2}{2 m}+\frac{p_p^2}{2 m}
$

Now applying conservation of momentum,

$
p_n+p_p=\frac{E}{C}
$

As $\mathrm{E}=\mathrm{B}$, equation (i) $p_n^2+p_p^2=0$
It only happens if $p_n=p_p$.

So, the equation. (ii) cannot be satisfied, and the process cannot take place.
Let us take $\mathrm{E}=\mathrm{B}+\mathrm{x}$, where $\mathrm{x} \ll \mathrm{B}$ for the process to take place.
Putting the value of p, from equation (ii), in equation (i), we get
or $2 p_p^2-\left(\frac{2 E}{c}\right) p_p+\left(\frac{E^2}{c^2}-2 m x\right)=0$

Solving the quadratic equation, we get

$
p_p=\frac{2 E}{c}+\frac{\sqrt{\frac{4 E^2}{c^2}-8\left(\frac{E^2}{c^2}-2 m x\right)}}{4}
$

For the real value $p_p$ the discriminant is positive

$
\begin{aligned}
& \frac{4 E^2}{c^2}=8\left(\frac{E^2}{c^2}-2 m x\right) \\
& 16 m x=\frac{4 E^2}{c^2} \\
& \Rightarrow x=\frac{E^2}{4 m c^2}
\end{aligned}
$

But $\mathrm{x} \ll \mathrm{B}$, hence $\mathrm{E} \cong \mathrm{B}$

$
\Rightarrow x \approx \frac{B^2}{4 m c^2}
$

Question:13.23

The deuteron is bound by nuclear forces just as H -atom is made up of $p$ and $e$ bound by electrostatic forces. If we consider the force between neutron and proton in deuteron as given in the form of a Coulomb potential but with an effective charge $e^{\prime}$ :

$
F=\frac{1}{4 \pi \varepsilon_0} \frac{e^{\prime 2}}{r}
$

estimate the value of $\left(e^{\prime} / e\right)$ given that the binding energy of a deuteron is 2.2 MeV.

Answer:

The binding energy is the H-atom

$
E=\frac{m e^4}{\pi \varepsilon_0^2 h^2}=13.6 \mathrm{eV}
$

If proton and neutron had charge $e^{\prime}$ each and were governed by the same electrostatic force, then in the above equation we would need to replace electronic mass $m$ by the reduced mass $m^{\prime}$ of proton-neutron and the electronic charge e by e'.

$\begin{aligned} m^{\prime} & =\frac{M \times N}{M+N}=\frac{M}{2} \\ & =\frac{1836 \mathrm{~m}}{2}=918 \mathrm{~m}\end{aligned}$

Here, $M$ represents the mass of a neutron/proton

$$
\therefore \quad \text { Binding energy }=\frac{918 m\left(e^{\prime}\right)^4}{8 \varepsilon_0^2 h^2}=2.2 \mathrm{MeV}
$$

Dividing Eqs. (ii) and (i), we get

$$
\begin{aligned}
918\left(\frac{e^{\prime}}{e}\right)^4 & =\frac{2.2 \mathrm{MeV}}{13.6 \mathrm{eV}}=\frac{2.2 \times 10^6}{13.6} \\
\left(\frac{e^{\prime}}{e}\right)^4 & =\frac{2.2 \times 10^6}{13.6 \times 918}=176.21 \\
\frac{e^{\prime}}{e} & =(176.21)^{1 / 4}=3.64
\end{aligned}
$$

Question:13.24

Before the neutrino hypothesis, the beta decay process was thought to be the transition,

$
n \rightarrow p+\bar{e}
$

If this was true, show that if the neutron was at rest, the proton and electron would emerge with fixed energies and calculate them. Experimentally, the electron energy was found to have a large range.

Answer:

Here, we have to observe the before and after cases of the $\beta$-decay. The neutron was at rest before $\beta$-decay. Therefore, energy of neutron E_n = m_nc^₂ and momentum(p_n) = 0
After $\beta$-decay, momentum of neutron (p_n)= momentum of proton (p_p) + momentum of electron (p_e)
pc= m_nc² – m_pc² = 938 MeV – 936 MeV = 2 MeV
Therefore, the Energy of the proton, E_p = 936 MeV
Therefore, the energy of the electron, E_e = 2.06 MeV

Question:13.25

The activity R of an unknown radioactive nuclide is measured at hourly intervals. The results found are tabulated as follows:

(i) Plot the graph of R versus t and calculate the half-life from the graph.
(ii) Plot the graph of ln(R/R0) versus t and obtain the value of half-life from the graph.

Answer:

From the above graph, we can clearly understand that a 50% reduction of R has happened. Therefore, the value of the half-life is 40 mins.
In the graph, the value of t = OB, which is equal to 40 mins.
ii)

The above graph is ln(R/R₀) versus t.
Here, the slope of the graph = – $\lambda$
Therefore, the value of $\lambda$ = -(-4.16-3.11)/1 = 1.05 h^-1
Now, Half-time(T_1/2) = 0.693/ $\lambda$ = 0.66 h = 39.6 min

Question:13.26

Nuclei with magic no. of proton Z = 2, 8, 20, 28, 50, 52 and magic no. of neutrons N = 2, 8, 20, 28, 50, 82 and 126 are found to be very stable
(i) Verify this by calculating the proton separation energy Sp for Sn¹²⁰(Z = 50) and Sb¹²¹ = (Z = 51). The proton separation energy for a nuclide is the minimum energy required to separate the least tightly bound proton from a nucleus of that nuclide. It is given by S_p = (M_Z-1, N + M_H – M_Z,N)c².

Given, $\quad \begin{gathered}{ }^{119} \mathrm{ln}=118.9058 \mathrm{u},{ }^{120} \mathrm{Sn}=199.902199 \mathrm{u}, \\ { }^{121} \mathrm{Sb}=120.903824 \mathrm{u},{ }^1 \mathrm{H}=1.0078252 \mathrm{u} .\end{gathered}$
(ii) What does the existence of a magic number indicate?

Answer:

(i) The proton separation energy is given by

$
\begin{aligned}
S_{p S n} & =\left(M_{119.70}+M_H-M_{120,70}\right) c^2 \\
& =(118.9058+1.0078252-119.902199) c^2 \\
& =0.0114362 c^2 \\
Similarly\ \ S_{p S p} & =\left(M_{120,70}+M_H-M_{121,70}\right) c^2 \\
& =(119.902199+1.0078252-120.903822) c^2 \\
& =0.0059912 c^2
\end{aligned}
$

Since $S_{p S n}>S_{p S b}, \mathrm{Sn}$ nucleus is more stable than the Sb nucleus.

(ii) The existence of magic numbers indicates that the shell structure of a nucleus is similar to the shell structure of an atom. This also explains the peaks in the binding energy/nucleon curve.