• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Exemplar Class 12 Physics Solutions Chapter 11 Dual Nature of Radiation and Matter

NCERT Exemplar Class 12 Physics Solutions Chapter 11 Dual Nature of Radiation and Matter

Edited By Safeer PP | Updated on Sep 14, 2022 01:13 PM IST | #CBSE Class 12th
Upcoming Event
CBSE Class 12th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Exemplar Class 12 Physics solutions chapter 11 contains a lot of topics in detail and gives a broader spectrum towards the dual nature of electromagnetic waves, and also gives an insight on different experiments conducted for proving such dual nature of electromagnetic waves. NCERT Exemplar Class 12 Physics chapter 11 solutions defines electromagnetic waves as a combination of packet or bundle of energy or quanta known as photons along with a brief description of photons, and its characteristics. It also explains the phenomenon of electron emission, work function, etc. Class 12 Physics NCERT Exemplar solutions chapter 11 provided here are very useful from an exam point of view. NCERT Exemplar Class 12 Physics solutions chapter 11 PDF download can also be brought into use.
Also see - NCERT Solutions for Class 12 Physics

This Story also Contains
  1. NCERT Exemplar Class 12 Physics Solutions Chapter 11 MCQI
  2. NCERT Exemplar Class 12 Physics Solutions Chapter 11 MCQII
  3. NCERT Exemplar Class 12 Physics Solutions Chapter 11 Very Short Answer
  4. NCERT Exemplar Class 12 Physics Solutions Chapter 11 Short Answer
  5. NCERT Exemplar Class 12 Physics Solutions Chapter 11 Long Answer
  6. Main Subtopics Covered in NCERT Exemplar Class 12 Physics Solutions Chapter 11 Dual Nature of Radiation and Matter
  7. What will the students learn in NCERT Exemplar Class 12 Physics Solutions Chapter 11?
  8. NCERT Exemplar Class 12 Physics Chapter Wise Links
  9. An Overview of Concepts Covered in NCERT Exemplar Class 12 Physics Solutions Chapter 11 Dual Nature of Radiation and Matter:

NCERT Exemplar Class 12 Physics Solutions Chapter 11 MCQI

Question:1

A particle is dropped from a height H. The de-Broglie wavelength of the particle as a function of height is proportional to (a) H (b) H1/2 (c) H0 (d) H-1/2

Answer:

The answer is the option (d)
Velocity of freely falling body after falling from a height H is given b
y v= \sqrt{2gH}
de-Broglie wavelength \lambda is given by
\lambda =\frac{h}{p}=\frac{h}{mv}\: or\: \frac{h}{m\sqrt{2gH}}
where h, m and g are constant
So,
\\\lambda \alpha \frac{1}{\sqrt{H}}\\ \lambda \alpha H^{-\frac{1}{2}}

Question:2

The wavelength of a photon needed to remove a proton from a nucleus which is bound to the nucleus with 1 MeV energy is nearly
a) 1.2 nm (b) 1.2 x 10-3 nm
(c) 1.2 x 10-6 nm (d). 1.2 x 10 nm

Answer:

The answer is the option (b)
Energy of the photon should be equal to the binding energy of the proton
So, the energy of photon=
1MeV=10^{6}\ast 1.6\ast 10^{-19}\\ \lambda=\frac{hc}{E}=6.63 \ast 10^{-34} \ast 3 \ast\frac{10^{8}}{1.6 \ast 10^{-13}}\\ =1.24 \ast 10^{-3}nm

Question:3

Consider a beam of electrons (each electron with energy E0) incident on a metal surface kept in an evacuated chamber. Then
(a) no electrons will be emitted as only photons can emit electrons
(b) electrons can be emitted but all with an energy, E0
(c) electrons can be emitted with any energy, with a maximum of E0 – \phi (\phi is the work function)
(d) electrons can be emitted with any energy, with a maximum of E0

Answer:

The answer is the option (d) When a beam of electrons (each electron with energy E0 ) incident on a metal surface is kept in an evacuated chamber, energy of incident electrons will be transferred to the emitted electrons due to elastic collisions. A part of E0 of incident electrons is consumed against work function to emit the electrons. Thus, the maximum energy of emitted electrons is E0

Question:4

Consider Fig. 11.7 in the NCERT textbook of physics for Class XII. Suppose the voltage applied to A is increased. The diffracted beam will have the maximum at a value of θ that
(a) will be larger than the earlier value
(b) will be the same as the earlier value
(c) will be less than the earlier value
(d) will depend on the target

Answer:

The answer is the option (c)
The de-Broglie wavelength of diffracted beam of electrons is given by
\lambda_{d}=\frac{12.27}{\sqrt{V}}A^{\circ}..............(i)
If there is a maxima of the diffracted electrons at an angle \theta, then 2d \sin \theta =\lambda
From equation (i), we get that on increasing the voltage, \lambda_{d} decreases which in turn
decreases the value of \theta

Question:5

A proton, a neutron, an electron and an α-particle have the same energy. Then their de Broglie wavelengths compare as
(a) \lambda _{p} = \lambda _{n} > \lambda _{e} > \lambda _{\alpha} \\ (b) \lambda _{\alpha} < \lambda _{p} = \lambda _{n} < \lambda _{e}\\ (c) \lambda _{e} < \lambda _{p} = \lambda _{n} > \lambda _{\alpha} \\ (d) \lambda _{e} = \lambda _{p} = \lambda _{n} = \lambda _{\alpha}

Answer:

The answer is the option (b)
de-Broglie wavelength \lambda is given by
\lambda=\frac{h}{p}=\frac{h}{mv}
2K=mv^{2}\\ 2Km=m^{2}v^{2}\\ 2mK=p^{2}\\ p=\sqrt{2mK}\\ y_{d}=\frac{h}{p}\\ y_{d}=\frac{h}{\sqrt{2mK}}\\ Since\: \lambda\alpha \frac{1}{\sqrt{m}}\\ M_{a}>m_{p}=m_{n}>m_{e}\\ \lambda_{a}>\lambda_{p}=\lambda_{n}>\lambda_{e}

Question:6

An electron is moving with an initial velocity v = v0i and is in a magnetic field B = B0j. Then, its de-Broglie wavelength
(a) remains constant
(b) increases with time
(c) decreases with time
(d) increases and decreases periodically

Answer:

The answer is the option (a)
\vec{v}=v_{0}\hat{i}\: \: \: \: \: B=B_{0}\hat{j}
Force on the elctron in perpendicular magnetic field B is
F=-e\left (\vec{v} X \vec{B} \right )
=-ev_{0}B_{0}k
Therefore, the force is perpendicular to v and B both. The de-Broglie wavelength will not change.

Question:7

An electron (mass m) with an initial velocity v = v0i(v0 > 0) is in an electric field E=E_{0}\hat{i} (E0 = constant > 0). Its de-Broglie wavelength at time t is given by
(a) \frac{\lambda_{0}}{\left [ 1+\frac{eE_{0}}{m}\frac{t}{v_{0}} \right ]}\\ (b)\lambda_{0}\left [ 1+\frac{eE_{0}t}{mv_{0}} \right ]\\ (c)\lambda_{0}\\ (d)\lambda_{0}t

Answer:

The answer is the option (a)
Initial de-Broglie wavelength \lambdais given by
\lambda_{0}=\frac{h}{p}=\frac{h}{mv_{0}}
Force on electron=F=qE
ma=eE_{0}\hat{i}\\ a=\frac{eE}{m}\hat{i}
Velocity of electron after time t is v=v0+at
v=v_{0}i+\frac{eE}{m}i.t\\ v=\left [ v_{0}+\frac{eEt}{m} \right ]\hat{i}\\
New de-Broglie wavelength
\lambda=\frac{h}{mv}
\lambda=\frac{h}{m\left [ v_{0}+\frac{eE_{0}t}{m} \right ]}\\ \lambda=\frac{\lambda_{0}}{\left [ 1+\frac{eE_{0}t}{mv_{0}} \right ]}\; \; \; \left ( Since \frac{h}{mv_{0}}=\lambda_{0} \right )

Question:8

An electron (mass m) with an initial velocity v=v_{0}\hat{i} is in an electric field E=E_{0}\hat{i} IF \lambda_{0}=\frac{h}{mv_{0}} its de-broglie wavelength at time t is given by
(a)\lambda_{0}\\(b)\lambda_{0}\sqrt{1+\frac{e^{2}E_{0}^{2}t^{0}}{m^{2}v_{0}^{2}}}\\(c)\frac{\lambda_{0}}{\sqrt{1+\frac{e^{2}E_{0}^{2}t^{0}}{m^{2}v_{0}^{2}}}}\\ (d)\frac{\lambda_{0}}{\left (1+\frac{e^{2}E_{0}^{2}t^{0}}{m^{2}v_{0}^{2}} \right )}

Answer:

The correct answer is option (c)
\frac{\lambda_{0}}{\sqrt{1+\frac{e^{2}E_{0}^{2}t^{0}}{m^{2}v_{0}^{2}}}}

NCERT Exemplar Class 12 Physics Solutions Chapter 11 MCQII

Question:9

Relativistic corrections become necessary when the expression for the kinetic energy 1/2 mv2 , becomes comparable with mc2, where m is the mass of the particle. At what de Broglie wavelength will relativistic corrections become important for an electron?
(a)\lambda=10nm\\ (b)\lambda=10^{-1}\\ (c)\lambda=10^{-4}\\ (d)\lambda=10^{-6}\\

Answer:

The answer is the option (c, d)
The wavelength of de-Broglie wave is given by
\lambda = h/p = h/mv
Here, h=6.6*10-34
and for electron, m=9*10-31 Kg
v=\frac{h}{m\lambda}\\ =6.6 * \frac{10^{-34}}{9*10^{-31}\lambda}\\ =6.6*\frac{10^{-34+31}}{9\lambda}=0.73*\frac{10^{-3}}{\lambda}......(i)
(a)\lambda=10nm=10^{-8}m\\ using \; the\; formula\;(i)v=7.3*10^{4}<3*10^{8}\\ (b)\lambda=10^{-1}nm=10^{-10}m\\ v=7.3*10^{6}<10^{8}\\ ({c})\lambda=10^{-4}nm=10^{-13}m\\ v=7.3*10^{9}>10^{8}\\ (d)\lambda=10^{-6}nm=10^{-15}m\\ v=7.3*10^{11}>10^{8}\\

Question:10

Two particles A1 and A2 of masses m1, m2 (m1 > m2) have the same de Broglie wavelength. Then
(a) their momenta are the same
(b) their energies are the same
(c) energy of A1 is less than the energy of A2
(d) energy of A1 is more than the energy of A2

Answer:

The answer is the option (a. c)
\lambda=\frac{h}{p}\\ p=\frac{h}{\lambda}\;or\; p\alpha \frac{1}{\lambda}\\ \frac{p_{1}}{p_{2}}=\frac{\lambda_{2}}{\lambda_{1}}\\ \lambda_{1}=\lambda_{2}=\lambda (given) p_{1}=p_{2} \; vertifies(a)\\ E_{a}=\frac{1}{2}mv^{2}=\frac{\frac{1}{2}m^{2}v^{2}}{m}=\frac{p^{2}}{2m}\\ E\alpha \frac{1}{m}[as\;p_{1}=p_{2}]\\ \frac{E_{1}}{E_{2}}=\frac{m_{2}}{m_{1}}\\ \frac{E_{1}}{E_{2}}<1[m_{1}>m_{2}] E_{2}>E_{1}
Thus c is correct.

Question:11

The de Broglie wavelength of a photon is twice the de Broglie wavelength of an electron. The speed of the electron is ve = c/100. Then
(a) Ee/Ep = 10-4
(b) Ee/Ep = 10-2
(c) Pe/mec = 10-2
(d) Pe/mec = 10-4

Answer:

The answer is the option (b,c)
The energy of a charged particle when accelerated through a potential difference V is:
E=\frac{1}{2}mv^{2}=qV
De-Broglie wavelength
\lambda=\frac{h}{p}=\frac{h}{\sqrt{2mE}}=\frac{h}{\sqrt{2mqV}}\\ \lambda_{Neutron}=\frac{0.286*10^{-10}}{\sqrt{E}}m=\frac{0.286*10^{-10}}{\sqrt{E}}A^{\circ}
At ordinary temperature, the energy of thermal neutrons
E=kT\Rightarrow \lambda=\frac{h}{\sqrt{2mkT}}\\ \lambda_{Thermal\; Neutron}=\frac{30.83}{\sqrt{T}}A^{\circ}\\ Mass\; of\; electron=m_{e}\\ Mass\; of\; photon=m_{p}\\
de Broglie wavelength of the electron
\lambda_{e}=\frac{h}{m_{e}v_{e}}=\frac{100h}{m_{e}c}\\ KE_{e}=\frac{1}{2}m_{e}v_{e}^{2}\\ m_{e}v_{e}^{2}=\sqrt{2E_{e}m_{e}}\\ \lambda_{e}=\frac{h}{m_{e}v_{e}}=\frac{h}{\sqrt{2E_{e}m_{e}}}\\ E_{e}=\frac{h^{2}}{2\lambda_{e}^{2}v_{e}}
de Broglie wavelength of the proton is \lambda_{p}
E_{p}=\frac{hc}{\lambda_{p}}=\frac{hc}{2\lambda_{e}}\\ \frac{E_{p}}{E_{e}}=\left ( \frac{hc}{\lambda_{e}} \right )*\left ( \frac{2\lambda_{e}^{2}m_{e}}{h} \right )=100\\ p_{e}=m_{e}v_{e}=m_{e}*\frac{c}{100}\\ \frac{p_{e}}{m_{e}c}=10^{-2}

Question:12

Photons absorbed in the matter are converted to heat. A source emitting n photon/sec of frequency ν is used to convert 1kg of ice at 0°C to water at 0°C. Then, the time T taken for the conversion
(a) decreases with increasing n, with ν fixed
(b) decreases with n fixed, ν increasing
(c) remains constant with n and ν changing such that nν = constant
(d) increases when the product nν increases

Answer:

The answer is the option (a, b. c).
Heat energy required to convert 1Kg of ice at 0^{\circ} C to water at 0^{\circ} C is E=mL
If n is the number of photons incident per second and time t is taken by radiation to
melt the ice at 0^{\circ}C.
Then E=n hv t
t=\frac{mL}{nhv}\\
Or t\alpha \frac{1}{nv}\\
[m, L and h are constants ] Hence, (a), (b) and (c) are correct.
If nv increases then T decreases ;so (d) isn't correct.

Question:13

A particle moves in a closed orbit around the origin, due to a force which is directed towards the origin. The de-BrOglie wavelength of the particle varies cyclically between two values \lambda_{1},\lambda_{2} with \lambda_{1}>\lambda_{2} Which of the following statements are true?
(a) The particle could be moving in a circular orbit with origin as centre
(b) The particle could be moving in an elliptic orbit with origin as its focus
(c) When the de-Broglie wavetength is \lambda_{1} the particle is nearer the origin than when its value is \lambda_{2}
(d) When the de-Broglie wavelength is \lambda_{2} the particle is nearer the origin than when its value is \lambda_{1}

Answer:

The answer is the option (b,d)
A particle moving in an elliptic orbit with Origin as the centre can have its de-Broglie wavelength varying between \lambda_{1} and \lambda_{2} cyclically. When the de-Broglie wavelength is lower, the particle is closer to the origin.
\lambda_{1}=\frac{h}{mv_{1}}\; and \; \lambda_{2}=\frac{h}{mv_{2}}\\ As,\lambda_{1}>\lambda_{2}\\ v_{2}>v_{1}
The particle will have a higher velocity closer to focus.

NCERT Exemplar Class 12 Physics Solutions Chapter 11 Very Short Answer

Question:14

A proton and an \alpha-particle are accelerated, using the same potential difference. How are the de Broglie wavelengths \lambda_{p} and \lambda_{a} related to each other?

Answer:

It is given that the proton and \alpha-particle are accelerated at the
same potential difference so their kinetic energies will be equal.
K_{1}=K_{2}=K=qV\\ \lambda=\frac{h}{\sqrt{2mK}}=\frac{h}{\sqrt{2mqV}}\\ \frac{\lambda_{p}}{\lambda_{a}}=\sqrt{\frac{m_{a}q_{a}V_{a}}{m_{p}q_{p}V_{p}}}\\ m_{a}=4m_{p};q_{a}=2e;q_{p}=e;V_{p}=V_{a}=V\\ \frac{\lambda_{p}}{\lambda_{a}}=\sqrt{\frac{4m_{p}2eV}{m_{p}eV}}=\sqrt{8}\\ \lambda_{p}=\sqrt{8}\lambda_{\alpha }

Question:15

(i) In the explanation of photoeletric effect, we assume one photon of frequency v collides with an electron and transfers its energy. This leads . to the equation for the maximum energy Emax of the emitted electron as E_{max} = hv - \phi_{0}
where \phi_{0} is the work function of the metal. If an electron absorbs 2 photons (each of frequency v), what will be the maximum energy for the emitted electron?
(ii) Why is this fact (two photon absorption) not taken into consideration in our discussion of the stopping potential?

Answer:

(i) In the question, 2 photons transfer its energy to one electron as E=hv
Ee=Ep
hve=2hv
ve=2v
v is the frequency
The maximum energy of the emitted electron is Emax=hve - \phi_{0}
=h(2v) - \phi_{0}
=2hv - \phi_{0}
(ii) Due to the mass difference, the probability that the electron absorbs 2 photons is extremely low. Therefore the chances of such emission of electrons is close to negligible.

Question:16

There are materials which absorb photons of shorter wavelength and emit photons of longer wavelength. Can there be stable substances which absorb photons of larger wavelength and emit light of shorter wavelength?

Answer:

With an increase in the wavelength of the photon, there is a decrease in the frequency or increase in the energy of the photon. Let us consider 2 possible cases:
  1. The photons having a smaller wavelength emit photons of smaller energy wherein some of it is consumed against work function. The law of conservation of energy is upheld in this case.
  2. Photons having a longer wavelength always emit photons with shorter wavelength. Photons having smaller energy can never emit photons of larger energy as some part of energy is consumed in work function of metal. So, it isn’t possible in stable materials.

Question:17

Do all the electrons that absorb a photon comes out as photo electrons?

Answer:

A common observation in the photoelectric effect is that most of the electrons knocked by photons are scattered into the metal by absorbing photons. In order to escape from the surface, the electron must absorb enough energy to overcome the positive ion attraction in the material of the surface.
Therefore, not all the electrons that absorb a photon comes out from the metal surface.

Question:18

There are two sources of light, each emitting with a power of 100 W. One emits X-rays of wavelength 1nm and the other visible light at 500 nm. Find the ratio of a number of photons of X-rays to the photons of visible light of the given wavelength?

Answer:

Let EX and EV be the energies given by one photon in X-rays and
visible rays respectively.
Then EX=hvX and EV=hvV
Let nX and nV be the number of photons from x-rays and visible
light are of equal energies and they emit 100 W power.
n_{X}hv_{X}=n_{V}hv_{V}\\ \frac{n_{X}}{n_{V}}=\frac{v_{V}}{v_{X}}=\frac{\lambda_{X}}{\lambda_{V}}\\ \frac{n_{X}}{n_{V}}=\frac{1}{500}\; \; \; n_{X}:n_{V}=1:500

NCERT Exemplar Class 12 Physics Solutions Chapter 11 Short Answer

Question:19

Consider the figure given for photoemission. How would you reconcile with momentum-conservation? Note light (photons) have momentum in a different direction than the emitted electrons.

Answer:

There is a transfer of momentum to the atoms on the metal surface when the photons strike the surface. This also results in a decrease in speed of the photons. Thus, the momentum of photons is transferred to the nucleus and electrons of the metal.
Although the direction of emission of electrons is opposite to that of photons, the total momentum transferred by them is equal.

Question:20

Consider a metal exposed to light of wavelength 600 nm. The maximum energy of the electron doubles when light of wavelength 400 nm is used. Find the work function in eV.

Answer:

Let the maximum energies of emitted electrons be K1 and K2 when 600 nm and 400 nm visible light are used according to question
K_{2}=2K_{1}\\ K_{max}=hv-\phi=\frac{hc}{\lambda}-\phi\\ K_{1}=\frac{hc}{\lambda_{1}}-\phi\\ K_{2}=\frac{hc}{\lambda_{2}}-\phi=2K_{1}\\ \frac{hc}{\lambda_{2}}-\phi=2 \left [\frac{hc}{\lambda_{1}}-\phi \right ]=\frac{2hc}{\lambda_{1}}-2\phi\\ \phi=hc\left [ \frac{2}{\lambda_{1}}- \frac{1}{\lambda_{2}} \right ]\\ =1240\left [ \frac{2}{600}-\frac{1}{400} \right ]eV\\ =\frac{1240}{200}\left [ \frac{2}{3}-\frac{1}{2} \right ]=6.2\left ( \frac{4-3}{6} \right )\\ Work\; function\; \phi=\frac{6.2}{6}=1.03eV

Question:21

Assuming an electron is confined to a 1nm wide region, find the uncertainty in momentum using the Heisenberg Uncertainty principle. You can assume the uncertainty in position as 1nm. Assuming , find the energy of the electron in electron volts.

Answer:

As the electrons rotate in a circular path,
\Delta r=1nm=10^{-9}m
\Delta p=\frac{h}{\Delta X}\\ \Delta p=\left ( \frac{331}{314} \right )*10^{25}\\ E=\frac{1}{2}mv^{2}=\frac{\Delta p^{2}}{2m}\\ E=3.8*10^{-2}eV

Question:22

Two monochromatic beams A and B of equal intensity I, hit a screen. The number of photons hitting the screen by beam A is twice that by beam B. Then what inference can you make about their frequencies?

Answer:

I_{A}=I_{B}\; (Given\; in\; the\; question)\\ n_{A}hv_{A}=n_{B}hv_{B}\\ n_{A}=2n_{B}[Given]\\ 2n_{B}v_{A}=n_{B}v_{B}\\ 2v_{A}=v_{B}
So, the frequency of source B is twice the frequency of source A.

Question:23

Two particles A and B of de Broglie wavelengths \lambda_{1} and \lambda_{2} combine to form a particle C. The process conserves momentum. Find the de Broglie wavelength of the particle C. (The motion is one dimensional).

Answer:

The de-Broglie wavelength is given by
\lambda=\frac{h}{p} \; or\; p=\frac{h}{\lambda}
p_{1}=\frac{h}{\lambda_{1}}, p_{2}=\frac{h}{\lambda_{2}}, p_{3}=\frac{h}{\lambda_{3}}
By the law of conservation of momentum
p_{1}+p_{2}= p_{3}
\frac{h}{\lambda_{1}}+\frac{h}{\lambda_{2}}=\frac{h}{\lambda_{3}} (\lambda_{3} is the wavelength of particle C)

\frac{h}{\lambda_{1}}+\frac{h}{\lambda_{2}}=\frac{h}{\lambda_{3}}\\ \frac{\lambda_{2}+\lambda_{1}}{\lambda_{1}\lambda_{2}}=\frac{h}{\lambda_{3}}
Case I:When p1 and p2 are positive then \lambda_{3}=\frac{\lambda_{1}\lambda_{2}}{\lambda_{1}+\lambda_{2}}
Case II:When p1 and p2 both are negative \lambda_{3}=\left |-\frac{\lambda_{1}\lambda_{2}}{\lambda_{1}+\lambda_{2}} \right |=\frac{\lambda_{1}\lambda_{2}}{\lambda_{1}+\lambda_{2}}
Case III: p_{A}>0,p_{B} <0
\frac{h}{\lambda_{3}}=\frac{h}{\lambda_{1}}-\frac{h}{\lambda_{2}}\; or\; \frac{h}{\lambda_{3}}=\frac{(\lambda_{2}-\lambda_{1})h}{\lambda_{1}\lambda_{2}}
Case IV: p_{A}<0,p_{B} >0
\frac{h}{\lambda_{3}}=\frac{h}{\lambda_{1}}-\frac{h}{\lambda_{2}}=\frac{\left (\lambda_{1}-\lambda_{2} \right )h}{\lambda_{1}\lambda_{2}}\\ \lambda_{3}=\frac{\lambda_{1}\lambda_{2}}{\lambda_{1}-\lambda_{2} }

Question:24

A neutron beam of energy E scatters from atoms on a surface with a spacing d = 0.1nm. The first maximum of intensity in the reflected beam occurs at theta = 30 degree. What is the kinetic energy E of the beam in eV?

Answer:

According to the Bragg’s law of diffraction, condition for the nth maxima is given by
2d\sin \theta=n \lambda\\\\ n=1\\\\ so\; \lambda=2d\sin \theta [\theta=30^{\circ}]\\\\ =2*0.1*10^{-9}\sin 30^{\circ}\\\\ p=\frac{h}{\lambda}=6.6*\frac{10^{-34}}{10^{-10}}=6.6*10^{-24}kg\frac{m}{s}\\\\ E=\frac{1}{2}mv^{2}=\frac{\frac{1}{2}m^{2}v^{2}}{m}\\\\ =\frac{p^{2}}{2m}=\frac{6.6*6.6*10^{-48}}{2*1.6*10^{-27}*1.6*10^{-19}}eV\\ =\frac{66*66*10^{-48+46}}{2*16*16}=33*\frac{33}{126}*10^{-2}\\\\ =8.5*10^{-2}=0.085eV

NCERT Exemplar Class 12 Physics Solutions Chapter 11 Long Answer

Question:25

Consider a thin target (10–2m square, 10–3m thickness) of sodium, which produces a photocurrent of 100 \mu A when a light of intensity 100W/m2 (\lambda = 660nm) falls on it. Find the probability that a photoelectron is produced when a photon strikes a sodium atom. [Take density of Na = 0.97 kg/m3].

Answer:

Area (A)=10-2 cm2=10-4m2
thickness (t)=10-3m
photo current (i)=100*10-6=10-4A
Intensity (I)=100 W/m2
wavelength (\lambda)=660 nm=660*10-9m
density (ρNa)=0.97 kg/m3
Avogadro's Number=6*1026Kg atom
Volume of target (V)=A*d=10-4*10-3=10-7m3
MNa (6*1026 atoms of Na)=23 kg
VNa (6*1026 atoms of Na) =
\frac{23}{0.97}m^{3}
NNa=
\frac{10^{-7}}{\frac{\frac{23}{0.97}}{6*10^{26}}}=2.53*10^{18}
Energy of photon=\frac{hc}{\lambda}
Total Energy=\frac{nhc}{\lambda}=IA
n=\frac{nA\lambda}{hc}=3.3*10^{16}\\\\ N=n*N_{Na}*p\\ i=Ne=n*N_{Na}*p*e\\ 10^{-4}=33*10^{16}*2.53*10^{18}*1.6*10^{-19}*p\\ p=7.48*10^{-21}

Question:26

Consider an electron in front of the metallic surface at a distance d (treated as an infinite plane surface). Assume the force of attraction by the plate is given as 2 2 0 1 4 4 q \pi\epsilon d Calculate work in taking the charge to an infinite distance from the plate. Taking d = 0.1nm, find the work done in electron volts. [Such a force law is not valid for d < 0.1nm].

Answer:

a-26
Let us consider the above-given figure wherein an electron is displaced slowly by a distance x by the means of an external force which is given by
F=\frac{q^{2}}{4*4\pi\varepsilon_{0}d^{2}}\; where \;d=0.1nm=10^{-10}m
Now work done by an external agency in taking the electron from distance d to infinity is
W=\int_{d}^{\infty }F_{x}dx=\int_{d}^{\infty }\frac{q^{2}dx}{4*4\pi\varepsilon _{0}}*\frac{1}{x^{2}}\\\\\\ =\frac{q^{2}dx}{4*4\pi\varepsilon _{0}}\left (\frac{1}{d} \right )=\frac{\left ( 1.6*10^{-19} \right )^{2}}{1.6*10^{-19}}*\frac{\left ( 9*10^{9} \right )}{4*10^{-10}}=3.6eV

Question:27

A student performs an experiment on photoelectric effect, using two materials A and B. A plot of Vstop versus v is given in figure.

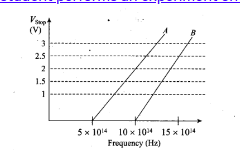
rtegte

(i) Which material A or B has a higher work function?

(ii)Given the electric charge of an electron = 1.6 x 10-19C, find the value of h obtained from the experiment for both A and B. Comment on whether it is consistent with Einstein's theory.

Answer:

We know that \phi_{0}=hv_{0} where v0=Threshold frequency
\frac{\phi_{0A}}{\phi_{0B}}=\frac{hv_{0A}}{hv_{0B}}=\frac{5*10^{14}}{10*10^{14}}=\frac{1}{2}\\ So\;\phi_{0B}=2\phi_{0A}
(ii) By the differentiation of potential
V=\frac{W}{Q}
hv=eV
Differentiating both the sides we get h.dv=edV
h=\frac{edV}{dv}
Using this formula
For metal A, h=6*10-34Js….(i)
For metal B, h=0.8*10-33…(ii)
Since the value of plank'sconstant is not equal for both the experimental graphs, the experiment inconsistent with Einstein's theory. But the values are very close to 6.6*10-34Js due to experimental limitation and hence can be considered consistent with Einstein theory.

Question:28

A particle A with a mass mA is moving with a velocity v and hits a particle B (mass mB) at rest (one dimensional motion). Find the change in the de Broglie wavelength of the particle A. Treat the collision as elastic.

Answer:

When the collision is elastic, law of conservation of momentum is followed.
m_{A}v+m_{B}0=m_{A}v_{1}+m_{B}v_{2}\\ m_{A}\left ( v-v_{1} \right )=m_{B}v_{2}\\ \frac{1}{2}m_{A}v_{2}= \frac{1}{2}m_{A}v_{1}^{2}+\frac{1}{2}m_{B}v_{2}^{2}\\ v_{1}=\frac{m_{A}-m_{B}}{\left ( m_{A}-m_{B} \right )}v\;\;\;v_{2}=\frac{2m_{A}}{\left ( m_{A}-m_{B} \right )}v\\\\ \lambda_{initial}=\frac{h}{m_{A}v}\\ \lambda_{final}=\frac{h}{m_{A}v_{1}}\\ \Delta \lambda=\lambda_{final}-\lambda_{initial}=\frac{h}{m_{A}v}\left [ \frac{m_{A}+m_{B}}{m_{A}-m_{B}}-1 \right ]

Question:29

Consider a 20 W bulb emitting light of wavelength 5000 A^{\circ} and shining on a metal surface kept at a distance 2m. Assume that the metal surface has work function of 2 eV and that each atom on the metal surface can be treated as a circular disk of radius 1.5 A^{\circ} .
(i) Estimate no. of photons emitted by the bulb per second. [Assume no other losses]
(ii) Will there be photoelectric emission?
(iii) How much time would be required by the atomic disk to receive energy equal to work function (2 eV)?
(iv) How many photons would atomic disk receive within time duration calculated in (iii) above?
(v) Can you explain how photoelectric effect was observed instantaneously?

Answer:

Given that P=20W
\lambda=5000A^{\circ}=5000*10^{-10}m\\ d=2m\\ \phi =2ev\\ r=1.5*10^{10}m\\
i) Number of photon emitted by bulb per second=
\frac{p \lambda}{hc}=5*10^{19}sec
ii Energy of the incident photon=
\frac{hc}{ \lambda}=2.48\;eV
iii Time required by the atomic disk to recieve energy is=28.4 sec
Let the time spent be \Delta T
E=P*A*\Delta t=P*\pi r^{2}\Delta t
Energy transferred by the bulb in full solid angle to atoms=
4\pi d^{2}\phi
p*\pi r^{2}\Delta t=4 \pi d^{2}\phi \Delta t=\frac{4d^{2}\phi}{Pr^{2}}=\frac{4*2*2*2*1.6*10^{-10}}{20*1.5*1.5*10^{-10}*10^{-10}}sec=\frac{12.8*10^{-19+20}}{5*2.25}
(iv) Number of photon received by the atomic disk=N
\frac{n_{1}\pi r^{2}\Delta t}{4\pi d^{2}}=\frac{n_{1}r^{2}\Delta t}{4d^{2}}\\ \\ =\frac{5 *10^{19}*1.5*1.5*10^{-20}*11.4}{4*2*2}
\approx 0.80\cong 1 photon per atom
(iv) We say that photoelectric emission is instantaneous as it involves a collision between the incident photon and free-electron lasting for a very short span of time, say \leq 10^{-9} sec

Main Subtopics Covered in NCERT Exemplar Class 12 Physics Solutions Chapter 11 Dual Nature of Radiation and Matter

  • Introduction
  • Electron emission
  • Photoelectric effect
  • Hertz’s observations
  • Hallwachs’ and Lenard’s observations
  • Experimental study of photoelectric effect
  • Effect of intensity of light on Photo current
  • Effect of potential on photoelectric current
  • Effect of frequency of incident radiation on stopping potential
  • Photoelectric effect and wave theory of light
  • Einstein’s photoelectric equation: Energy quantum of radiation
  • Particle nature of light: The photon
  • Wave nature of matter
  • Davisson and Germer Experiment

What will the students learn in NCERT Exemplar Class 12 Physics Solutions Chapter 11?

The students will be able to learn various questions related to different things about the nature of electromagnetic waves and how their nature can help and make the process of different phenomena possible. NCERT Exemplar solutions for Class 12 Physics chapter 11 also deals with various different experimentation used to prove the dual nature of electromagnetic waves which gives the learners an insight on the emergence of such principles and how they were used further for deriving useful knowledge out of it. Learners will also learn about different developments at different periods of time by different people about the nature of electromagnetic waves and their sequence. NCERT Exemplar Class 12 Physics solutions chapter 11 will also give a lot of knowledge about the wave theory of light, which will enlighten and provide them with a logical explanation for various phenomena happening around them in real life.

NCERT Exemplar Class 12 Physics Chapter Wise Links

An Overview of Concepts Covered in NCERT Exemplar Class 12 Physics Solutions Chapter 11 Dual Nature of Radiation and Matter:

  • NCERT Exemplar Class 12 Physics chapter 11 solutions give a brief description about one of the most important experiments done by Hertz in 1887 regarding the photoelectric effect and accorded four crucial observations about the effect of intensity of light on photocurrent, effect to potential on photocurrent, the effect of frequency of incidence on stopping potential and stopping potential doesn’t depend on incident intensity.
  • Class 12 Physics NCERT Exemplar solutions chapter 11 also explored the experiment done by Einstein about the photoelectric effect which gave the formula for the kinetic energy required by electrons to leave a metal surface and concluded that the incident frequency should be greater than the threshold frequency of the metal.
  • One other observation made in this chapter was the De Broglie hypothesis which ultimately suggested the dual nature of matter which was in agreement with the Heisenberg’s uncertainty principle.
  • The lesson concludes with the Davisson and Germer Experiment, which showed the deflection in the galvanometer being proportional to the intensity of the electric bean entering the detector.
Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

NCERT Exemplar Class 12 Solutions

Also, check the NCERT solutions of questions given in book

Also read NCERT Solution subject wise

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Must read NCERT Notes subject wise

Also Check NCERT Books and NCERT Syllabus here:

Frequently Asked Questions (FAQs)

1. How are these questions solved?

These questions are solved keeping in mind the CBSE pattern and how the marks are divided as per the steps.

2. Are these NCERT exemplar Class 12 Physics solutions chapter 11 downloadable?

Yes, one can download these questions so that one uses the solutions offline.

3. How to make most of the solutions?

Try to understand the NCERT exemplar solutions for Class 12 Physics chapter 11 and connect them to the topics that one has studied in the chapter.

4. What all things one will learn in this chapter?

 One will learn in detail about wave theory of light, particle nature of light, photoelectric effect, Davisson and Germer experiment, etc. 

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Gujarat Board Secondary School Certificate Examination

Late Fee Application Date:11 December,2024 - 20 December,2024

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Business Analytics Foundations
 Via PW Skills
Digital Banking Business Model
 Via State Bank of India
Full-Stack Android Development
 Via Masai School
Data Science for Beginners
 Via Board Infinity
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer
Jefferson 25 September,2024
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

  1. Re-evaluate Your Study Strategies:

    • Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
    • Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
    • Practice Regularly: Consistent practice is key to mastering chemistry.

  2. Consider Professional Help:

    • Tutoring: A tutor can provide personalized guidance and support.
    • Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.

  3. Explore Alternative Options:

    • Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
    • Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.

  4. Focus on NEET 2025 Preparation:

    • Stay Dedicated: Continue your NEET preparation with renewed determination.
    • Utilize Resources: Make use of study materials, online courses, and mock tests.

  5. Seek Support:

    • Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
    • Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.







Read Complete Answer
Kanishka kaushikii 17 September,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer
Yuvan 30 August,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Board Exams: States agree to equivalence; no question paper ‘jumbling’ from next year, says PARAKH CEO
December 12, 2024 - 12:44 PM IST
Board Exam Date 2025 Live: CBSE, ICSE, BSEB, MPBSE Class 10, 12 timetable out; Punjab, Rajasthan schedule soon
December 08, 2024 - 10:34 PM IST
CBSE Board Exams 2025: Guidelines issued for Class 10, 12 practicals
December 03, 2024 - 01:11 PM IST
Board Exam Date Sheet 2025 Live: ICSE, ISC, CBSE, MP time table out; BSEB routine soon
November 26, 2024 - 10:18 PM IST
Board exam dates 2025: CBSE, CISCE, UP, MP, Maharashtra, TN time table out; state-wise updates
November 25, 2024 - 08:42 PM IST
Board Exam Date Sheet 2025: CBSE, UPMSP, MPBSE, Class 10, 12 board exam dates out; BSEB, CGBSE schedules soon
November 22, 2024 - 10:04 PM IST
CBSE Date Sheet 2025 (Out) Live: Class 10, 12 board exam time table at cbse.gov.in; syllabus, sample papers
November 21, 2024 - 09:30 PM IST

Stay up-to date with CBSE Class 12th News

Back to top