• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Exemplar Class 12 Physics Solutions Chapter 10 Wave Optics

NCERT Exemplar Class 12 Physics Solutions Chapter 10 Wave Optics

Edited By Safeer PP | Updated on Sep 14, 2022 01:09 PM IST | #CBSE Class 12th
Upcoming Event
CBSE Class 12th  Exam Date : 01 Jan' 2025 - 14 Feb' 2025

NCERT Exemplar Class 12 Physics solutions chapter 10 deals with different mechanisms and phenomenon of waves for which the ray approximation of geometric optics is invalid. NCERT Exemplar Class 12 Physics chapter 10 solutions deal with the propagation of various principles of the wave, one of which includes the Huygens principle that derived various laws for reflection and refraction of waves with the help of a new term called a wavefront. The NCERT chapter Wave Optics also deals with diffraction, polaristion, interference etc. Class 12 Physics NCERT Exemplar solutions chapter 10 covers questions related to all the main topics of the chapter. NCERT Exemplar Class 12 Physics solutions chapter 10 PDF download is available to students for further use. These solutions will help the students in understanding the best approach to solving and answering a question. The topics and subtopics covered in this chapter, are as follows:

This Story also Contains
  1. NCERT Exemplar Class 12 Physics Solutions Chapter 10 MCQI
  2. NCERT Exemplar Class 12 Physics Solutions Chapter 10 MCQII
  3. NCERT Exemplar Class 12 Physics Solutions Chapter 10 Very Short Answer
  4. NCERT Exemplar Class 12 Physics Solutions Chapter 10 Short Answer
  5. NCERT Exemplar Class 12 Physics Solutions Chapter 10 Long Answer
  6. Main Subtopics Covered in NCERT Exemplar Class 12 Physics Solutions Chapter 10 Wave Optics
  7. NCERT Exemplar Class 12 Physics Chapter Wise Links
  8. Important Topics To Cover For Exams From NCERT Exemplar Class 12 Physics Solutions Chapter 10 Wave Optics
LiveJEE Main 2025 Live: Exam city slip soon at jeemain.nta.nic.in; admit card date, cut-off updatesDec 30, 2024 | 10:30 PM IST

Candidates can have a look at the JEE Main 2025 physics syllabus below.

JEE Main 2025 physics topics

Number of questions

Marks

Modern Physics

5

20

Heat and Thermodynamics

3

12

Optics

3

12

Current Electricity

3

12

Electrostatics

3

12

Magnetics

2

8

Unit, Dimension and Vector

1

4

Kinematics

1

4

Laws of Motion

1

4

Work, Power and Energy

1

4

Centre of Mass, Impulse, and Momentum

1

4

Rotation

1

4

Gravitation

1

4

Simple Harmonic Motion

1

4

Solids and Fluids

1

4

Waves

1

4

Electromagnetics Induction; AC

1

4

Read More

Also see - NCERT Solutions for Class 12 Physics

NCERT Exemplar Class 12 Physics Solutions Chapter 10 MCQI

Question:1

Consider a light beam incident from air to a glass slab at Brewster’s angle, as shown in Fig. 10.1. A Polaroid is placed in the path of the emergent ray at point P and rotated about an axis passing through the centre and perpendicular to the plane of the polaroid.


A. For a particular orientation, there shall be darkness as observed through the polaroid.
B. The intensity of light, as seen through the polaroid, shall be independent of the rotation.
C. The intensity of light, as seen through the polaroid, shall go through a minimum but not zero for two orientations of the polaroid.
D. The intensity of light, as seen through the polaroid shall go through a minimum for four orientations of the polaroid.

Answer:

The answer is the option (c)
Explanation: Brewster’s law states that when a beam of unpolarized light is reflected in a transparent medium, the resultant reflected light is completely polarized at a certain angle of incidence. It is given by:
From the figure, it is clear that
\theta p \;+ \theta \;r = 90^{\circ}

Also, n = \tan \theta \;p (Brewster’s law)

(i) For \;i < \theta \;p \;or\; i > \theta \;p
Both of the reflected and refracted light ray become partially polarized.

(ii) For glass\; \theta \;p = 51^{\circ} f\! or \; water\; \theta \;p = 53^{\circ}

Question:2

Consider sunlight incident on a slit of width 104 A. The image seen through the slit shall
A. be a fine sharp slit white in colour at the centre.
B. a bright slit white at the centre diffusing to zero intensities at the edges.
C. a bright slit white at the centre diffusing to regions of different colours.
D. only be a diffused slit white in colour.

Answer:

The answer is the option (a)
Diffraction is a phenomenon of bending of light rays around an obstacle or an aperture of a similar wavelength.

Question:3

Consider a ray of light incident from air onto a slab of glass (refractive index n) of width d, at an angle θ. The phase difference between the ray reflected by the top surface of the glass and the bottom surface is
A. \frac{4 \pi d}{\lambda}\left ( 1-\frac{1}{n^2}\sin^2 \theta \right )^{1/2}+\pi
B.\frac{4 \pi d}{\lambda}\left ( 1-\frac{1}{n^2}\sin^2 \theta \right )^{1/2}
C. \frac{4 \pi d}{\lambda}\left ( 1-\frac{1}{n^2}\sin^2 \theta \right )^{1/2}+\frac{\pi}{2}
D.\frac{4 \pi d}{\lambda}\left ( 1-\frac{1}{n^2}\sin^2 \theta \right )^{1/2}+2 \pi

Answer:

The answer is the option (a)

Question:4

In a Young’s double-slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case
A. there shall be alternate interference patterns of red and blue.
B. there shall be an interference pattern for red distinct from that for blue.
C. there shall be no interference fringes.
D. there shall be an interference pattern for red mixing with one for blue.

Answer:

The answer is the option (c)
Here, in this case, due to the presence of red and blue filters. The waves of light will only be Red and Blue. In YDSE, the monochromatic light is used for the formation of fringe on the screen. Therefore, in this case, there will be no interference.

Question:5

Figure 10.2 shows a standard two-slit arrangement with slits S1, S2. P1, P2 are the two minima points on either side of P (Fig. 10.2). At P2 on the screen, there is a hole and behind P2 is a second 2- slit arrangement with slits S3, S4 and a second screen behind them.


A. There would be no interference pattern on the second screen but it would be lighted.
B. The second screen would be totally dark.
C. There would be a single bright point on the second screen.
D. There would be a regular two slit pattern on the second screen

Answer:

The answer is the option (d)
Wavefront is the plane where every point on given wave front is the source of disturbance which are known as secondary wavelets.

The wavefront emitted by a narrow source is divided in two parts by reflection, refraction or diffraction. The coherent sources so obtained are imaginary.

NCERT Exemplar Class 12 Physics Solutions Chapter 10 MCQII

Question:6

Two source S1 and S2 of intensity I1 and I2 are placed in front of a screen [Fig. 10.3 (a)]. The pattern of intensity distribution seen in the central portion is given by Fig. 10.3 (b). In this case which of the following statements are true.



A. S1 and S2 have the same intensities.
B. S1 and S2 have a constant phase difference.
C. S1 and S2 have the same phase.
D. S1 and S2 have the same wavelength.

Answer:

The correct answers are the options (a, b, c)

Key concept:

For getting the sustained interference the initial phase difference between the interfering waves must remain constant, i.e., sources should be coherent.
for two coherent sources, the resultant intensity is given by
I=I_1+I_2+2\sqrt{I_1I_2}\cos\phi

Resultant intensity at the point of observation will be maximum.
\\I_{max}=I_1+I_2+2\sqrt{I_1I_2}\\\\ I_{max}=\left ( \sqrt{I_1}+\sqrt{I_2} \right )^{2}

Resultant intensity at the point of observation will be minimum.

\\I_{min}=I_1+I_2-2\sqrt{I_1I_2}\\\\ I_{min}=\left ( \sqrt{I_1}-\sqrt{I_2} \right )^{2}

Question:7

Consider sunlight incident on a pinhole of 103A. The image of the pinhole seen on a screen shall be
A. a sharp white ring.
B. different from a geometrical image.
C. a diffused central spot, white in colour.
D. diffused coloured region around a sharp central white spot.

Answer:

The correct answers are the options (b,d)
Diffraction of light can only be observed if the size of the aperture or obstacle is less than the wavelength of the light wave.
The given width of the pinhole is 103 angstrom. The wavelength of sunlight is 4000 angstrom to 8000 A. Therefore, the light is diffracted from the hole. And due to this, the image formed on the screen will be geometrically different.

Question:8

Consider the diffraction pattern for a small pinhole. As the size of the hole is increased
A. the size decreases.
B. the intensity increases.
C. the size increases.
D. the intensity decreases.

Answer:

The correct answers are the options (a, b)
Key concept: The 'shadow' of the hole of dimeter d is spread out over an angle
\Delta \theta =1.22\frac{\lambda}{D}\Rightarrow \Delta \theta\propto \frac{1}{D}

Question:9

For light diverging from a point source
A. the wavefront is spherical.
B. the intensity decreases in proportion to the distance squared.
C. the wavefront is parabolic.
D. the intensity at the wavefront does not depend on the distance

Answer:

The correct answers are the options (a, b)

Due to the point source light propagates in all direction symmetrically and hence, wavefront will be spherical.

As the intensity of the source will be

I\propto \frac{1}{r^{2}}

where r is the radius of the wavefront at any time.
Hence the intensity decreases in proportion to the distance squared.

NCERT Exemplar Class 12 Physics Solutions Chapter 10 Very Short Answer

Question:10

Is Huygens’s principle valid for longitudinal sound waves?

Answer:

The principle of Huygen’s is valid for longitudinal sound waves

Question:11

Consider a point at the focal point of a convergent lens. Another convergent lens of the short focal length is placed on the other side. What is the nature of the wavefronts emerging from the final image?

Answer:


Here the orientation of the rays is perpendicular to L1. It forms an image at I1, i.e. the focal length. Again, the image is converged and goes through L2 after which the final image is formed at I. The nature of the wavefronts emerging from the final image is Spherical.

Question:12

What is the shape of the wavefront on earth for sunlight?

Answer:

As the sun is at an exceptionally large distance from earth. Assuming it as a point source of light at infinity, as seen from earth, we can conclude that the radius of the wavefront from the sun to the earth is infinite. This would mean that the rays are perpendicular to earth and the wave front is almost a plane.

Question:13

Why is the diffraction of sound waves more evident in daily experience than that of a light wave?

Answer:

The wavelength of sound waves is 15 m to 15 mm for 20 Hz to 20,000 Hz respectively. Therefore, sound waves diffraction take place when the comparable size of the obstacle is confronted. While in the case of the light wave, the wavelength of visible light is 0.4 to 0.7 micron. So, the obstacles of this size are not easily present around us. Therefore, diffraction of light is not so evident in day to day life.

Question:14

The human eye has an approximate angular resolution of ? = 5.8×10–4 rad and a typical photo printer prints a minimum of 300 dpi (dots per inch, 1 inch = 2.54 cm). At what minimal distance z should a printed page be held so that one does not see the individual dots.

Answer:

It is given, angular resolution of human eye \phi =5.8 \times 10^{-4} rad and printer print 300 dots per inch.
The linear distance between the two dots is
l=\frac{2.54}{300} cm=0.84 \times 10^{-2}\; cm
At a distance of z cm, this subtends an angle,
\phi =\frac{l}{z}\\\\ z= \frac{l}{\phi }= \frac{0.84 \times 10^{-2}\;cm}{5.8 \times 10^{-4}}=14.5 \; cm
If a printed page be held at a distance of 14.5 cm, then one does not be able to see the individual dots.

Question:15

A polaroid (I) is placed in front of a monochromatic source. Another polaroid (II) is placed in front of this polaroid (I) and rotated till no light passes. A third polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II)? Explain.

Answer:

Monochromatic source of light is kept behind polaroid (I). Then some other polaroid (II) is placed in front of polaroid (I). SO, the axes of both polaroid are parallel to each other; the light passes through (II) unaffected.

Now polaroid (II) is rotated till no light passes. In this situation the pass axis of polaroid (II) is perpendicular to polaroid (I), then (I) and (II) are set in a crossed position. No light passes through a polaroid- (II)

Now third polaroid (III) is now placed in between (I) and (II). Only in the special cases when the pass axis of (III) is parallel to (I) or (II) there shall be no light emerging. In all other cases, there shall be light emerging because the pass axis of (II) is no longer perpendicular to the pass axis of (III).


Now, the polaroid (II) is rotated such that (I) and (II) are in a crossed position. Therefore, no light will pass through (II).

NCERT Exemplar Class 12 Physics Solutions Chapter 10 Short Answer

Question:16

Can reflection result in plane-polarized light if the light is incident on the interface from the side with higher refractive index?

Answer:

If Brewster’s angle is equal to the incident angle, then the transmitted light is slightly polarized, while the reflected light is plane-polarized.

Polarisation by reflection occurs when the angle of incidence is Brewster's angle.
i.e. \tan i_R = ^1 \mu_2 =\frac{\mu_2}{\mu_1} \; where\; \mu_2 < \mu_1
When the light rays travel in such a medium, the critical angle is
\sin i_e = \frac{\mu_2}{\mu_1} \; where\; \mu_2 < \mu_1\\\\ As \; \left | \tan i_B \right |>\left | \sin i_e \right | for \; large \; angles\; i_B>i_e
Thus the polarization by reflection occurs definitely.

Question:17

For the same objective, find the ratio of the least separation between two points to be distinguished by a microscope for the light of 5000 \AA and electrons accelerated through 100V used as the illuminating substance.

Answer:

5000 \AA = 5000 \times 10^{-10} m\\ \\ \frac{1}{d} = \frac{2 \sin \beta}{1.22 \lambda } \\\\ d\;min = \frac{1.22 \lambda}{2 \sin \beta}\\d_{min}=\frac{1.22\times5000\times10^{-10}}{2sin\beta}
When we use 100V light,
\lambda_d =\frac{1.27}{\sqrt{V}}nm=\frac{1.27}{\sqrt{100}}nm
d' min =\frac{1.22\lambda_d }{2 \sin \beta}
d'min = \frac{1.22 \times 1.27 \times 10 ^{-10} }{2 \sin \beta}
The required ratio =\frac{d \;min}{d'min} = \frac{1.22 }{5000} =0.244 \times 10^{-3}

Question:18

Consider a two-slit interference arrangement (Fig. 10.4) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of such that the first minima on the screen fall at a distance D from the centre O.

Answer:


S_1P = \sqrt{D^2} + (D - x)^2\\\\S_2P = \sqrt{D^2} +(D- x)^2 \\\ T_2P = D + x \\\ T_2P = D - x \\ \\ \left [ D^{2} +(D+x)^{2} \right ]^{1/2}- \left [ D^{2} +(D-x)^{2} \right ]^{-1/2} =\frac{\lambda}{2} \\\\D = 0.404 \lambda

NCERT Exemplar Class 12 Physics Solutions Chapter 10 Long Answer

Question:19

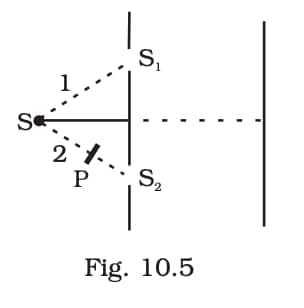
Figure 10.5 shown a two-slit arrangement with a source which emits unpolarised light. P is a polarizer with axis whose direction is not given. If I0 is the intensity of the principal maxima when no polarizer is present, calculate in the present case, the intensity of the principal maxima as well as of the first minima.

Answer:

The amplitude of wave in normal/perpendicular polarization
A\perp =A_{\perp }^{0}\left ( \sin\left ( kx- \omega t \right )+\sin (kx-\omega t+ \phi) \right )
The amplitude of wave in parallel polarization
A\parallel =A_{\parallel}^{0}\left ( \sin\left ( kx- \omega t \right )+\sin (kx-\omega t+ \phi) \right )
The intensity of the wave at the first minima with a polarizer
\left | A_{\perp }^{0} \right |^{2}\left ( 1-1 \right )+\frac{\left | A_{\perp }^{0} \right |^{2}}{2}= \frac{I_0}{8}

Question:20

A small transparent slab containing material of μ =1.5 is placed along AS2 (Fig.10.6). What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?

Answer:



For the principal maxima,(path difference is zero)
\\\Delta x=2d \sin \theta +\left [ (\mu -1)L \right ]=0\\ \sin \theta _0=-\frac{L(\mu-1)}{2d}=-\frac{-L(0.5)}{2d}[\therefore L=d/4]\\or\; \; \; \; \; \Rightarrow \sin \theta _0=\frac{-1}{16}
\theta _0 is the angular position corresponding to the principal maxima.
\Rightarrow \; \; \; OP=D\tan \theta _0\approx D \sin \theta _0=\frac{-D}{16}
For the first minima, the path difference is
\pm \frac{\lambda}{2}
\\\Delta x=2d\sin \theta _1+0.5L=\pm \frac{\lambda}{2}\\ \sin \theta _1=\frac{\pm \lambda/2-0.5L}{2d}=\frac{\pm \lambda/2-d/8}{2d}\\\\\Rightarrow \; \; \sin \theta _1=\frac{\pm \lambda/2-\lambda/8}{2\lambda}=\pm \frac{1}{4}-\frac{1}{16}

Question:21

Four identical monochromatic sources A, B, C, D, as shown in the (Fig.10.7) produce waves of the same wavelength and are coherent. Two receiver R1 and R2 are at great but equal distances from B.


(i) Which of the two receivers picks up the larger signal?
(ii) Which of the two receivers picks up the larger signal when B is turned off?
(iii) Which of the two receivers picks up the larger signal when D is turned off?
(iv) Which of the two receivers can distinguish which of the sources B or D has been turned off?

Answer:

(i) Let us consider the disturbances at the receiver R1, which is at a distance d from B.
Let the equation of wave at R1, because of A be
y_A=a \cos \omega t ......(i)
The path difference of the signal from A with that from B is \lambda/2 and hence, the phase difference
\Delta \phi = \frac{2\pi }{\lambda }\times \left ( path\;dif\! \! ference \right )=\frac{2\pi }{\lambda }\times \frac{\lambda }{2}
Thus, the wave equation at R1, because of B is
y_B=a \cos \left ( \omega t-\pi \right )= -a \cos \omega t ......(ii)
The path difference of the signal from C with that from A is \lambda and hence the phase difference
\Delta \phi = \frac{2\pi }{\lambda }\times \left ( path\;dif\! \! ference \right )=\frac{2\pi }{\lambda }\times \lambda=2 \pi
Thus, the wave equation at R1 because of C is
y_C=a \cos \omega t =a \cos\left ( \omega t-2\pi \right )= a \cos \omega t ......(iii)
The path difference between the signal from D with that of A is

\Delta _{x_{R_1}}= \sqrt{d^2+\left ( \frac{\lambda }{2} \right )^{2}}-\left (d- \frac{\lambda }{2} \right )=d\left ( 1+\frac{\lambda ^{2}}{4d^{2}} \right )^{1/2}-d+\frac{\lambda }{2}
=d\left ( 1+\frac{\lambda ^{2}}{8d^{2}} \right )-d.\frac{\lambda }{2}=\frac{\lambda }{2}\left ( \because d>>\lambda \right )
Therefore, phase difference is \pi
y_D=a \cos\left ( \omega t-\pi \right )= -a \cos \omega t ......(iii)
The resultant signal picked up at R_1, from all the four sources is the summation of all four waves,
y_{R_1}=y_A+y_B+y_C+y_D
y_{R_1}=a \cos \omega t-a \cos \omega t+a \cos \omega t-a \cos \omega t=0
Thus, the signal picked up at R1 is zero.
Now let us consider the resultant signal received at R2. Let the equation of wave at R2 . Let the equation
of wave at R2, because of B be
y_{B}=a_1 \cos \omega t
The path difference of the signal from from D with that from B is \frac{\lambda }{2} and
hence, the phase difference
\Delta \phi =\frac{2\pi }{\pi }\times \left ( \text {path difference} \right )=\frac{2\pi}{\lambda }\times \frac{\lambda }{2}=\pi
Thus, the wave equation at R_{2}, because of D is
y_{B}=a_{1}\cos \left ( \omega _{t}-\pi \right )=-a_{1}\cos\; \omega t\; \; \; \; \; \; \; \; \; \; \; \; \; ....(ii)
The path difference between signal at A and that at B is
\Delta x_{R_{2}}=\sqrt{\left ( d \right )^{2}+\left ( \frac{\lambda }{2} \right )^{2}}-d=d\left ( 1+\frac{\lambda ^{2}}{4d^{2}} \right )^{\frac{1}{2}}-d\simeq \frac{\lambda ^{2}}{8d^{2}}
As d>>\lambda , therefore this path differences \Delta x_{R_{2}}\rightarrow 0
and phase difference \Delta \phi =\frac{2\pi}{\lambda }\times \left ( \text {path difference} \right )
=\frac{2\pi}{\lambda }\times 0\rightarrow 0\left ( \text {very small} \right )=\phi \left ( \text {say} \right )
Hence, y_{B}=a_{1}\cos \left ( \omega _{t}-\phi \right )
Similarly, y_{B}=a_{1}\cos \left ( \omega _{t}-\phi \right )
The resultant signal picked up at R_{2}, from all the four sources is the summation of all four waves, y_{R_{2}}=y_{A}+y_{B}+y_{C}+y_{D}
y_{R_{2}}=a_{1}\cos \; \omega t-a_{1}\cos \omega t+a_{1}\cos\left ( \omega t-\phi \right )+a_{1}\cos \left ( \omega t-\phi \right )
= 2a_{1}\cos \left ( \omega t-\phi \right )
\therefore Signal picked up by R_{2} is y_{R_{2}}=2a_{1}\cos \left ( \omega t-\phi \right )
\therefore \left [ V_{R_{2}} \right ]^{2}=4a_{1}^{2}\cos^{2}\left ( \omega t-\phi \right )\Rightarrow \left \langle I_{R_{2}} \right \rangle=2a_{1}^{2}
Thus, R_{2} picks up the larger signal.
(ii) If B is switched off,
R_{1}, picks up y=a\cos \; \omega t
\therefore \left \langle I_{R_{1}} \right \rangle=a^{2}<\cos^{2}\omega t>=\frac{a^{2}}{2}
R_{2} picks up y=a\; \cos\; \omega t
\left \langle I_{R_{2}} \right \rangle=a^{2}<\cos^{2}\omega t>=\frac{a^{2}}{2}
Thus , R_{1} and R_{2} pick up the same signal
(iii) If D is switched off.
R_{1} picks up y=a\; \cos\; \omega t
\therefore \left \langle I_{R_{1}} \right \rangle=\frac{1}{2}a^{2}
R_{2} picks up y=3a\; \cos\; \omega t
\therefore \left \langle I_{R_{2}} \right \rangle=9a^{2}<\cos^{2}\omega t>=\frac{9a^{2}}{2}
Thus, R_{2} picks up larger signal compared to R_{1}.
(iv) Thus, a signal at R_{1} indicates B has been switched off and an enhanced signal at R_{2} indicates D has been switched off.

Question:22

The optical properties of a medium are governed by the relative permittivity (εr) and relative permeability (μr ). The refractive index is defined as \sqrt{\mu, \epsilon }=n For ordinary material εr > 0 and μr > 0, and the positive sign is taken for the square root. In 1964, a Russian scientist V. Veselago postulated the existence of material with εr < 0 and μr < 0. Since then, such ‘metamaterials’ have been produced in the laboratories and their optical properties studied. For such materials n=\sqrt{\mu, \epsilon }
As light enters a medium of such refractive index, the phases travel away from the direction of propagation.

(i) According to the description above shows that if rays of light enter such a medium from the air (refractive index = 1) at an angle in 2nd quadrant, them the refracted beam is in the 3rd quadrant.
(ii) Prove that Snell’s law holds for such a medium.

Answer:



Again consider figure (i), let AB represent the incident wavefront and DE represent the refracted wavefront. All point on a wavefront must be in same phase and in turn, must have the same optical path length.
\\Thus\; \; \; \; \; -\sqrt{\epsilon_r \mu_r }AE=BC -\sqrt{\epsilon_r \mu_r }CD\\\\Or\; \; \; \; \; BC=\sqrt{\epsilon_r \mu_r }\left ( CD-AE \right )\\\\BC>0,CD>AE
As showing that the postulate is reasonable. If however, the light proceeded in the sense it does for ordinary material (viz. in the fourth quadrant, Fig.2)
\\Then\; \; \; \; \; -\sqrt{\epsilon_r \mu_r }AE=BC -\sqrt{\epsilon_r \mu_r }CD\\\\Or\; \; \; \; \; BC=\sqrt{\epsilon_r \mu_r }\left ( CD-AE \right )\\\\i\! f \; \; \; \; BC>0,then \;CD>AE
Which is obvious from Fig. (i). Hence, the postulate is reasonable.
However, if the light proceeds in the sense it does for ordinary material, (going from the second quadrant to 4th quadrant)as shown in Fig. (i). then proceeding as above,
-\sqrt{\epsilon_r \mu_r }AE=BC -\sqrt{\epsilon_r \mu_r }CD\\\\Or\; \; \; \; \; BC=\sqrt{\epsilon_r \mu_r }\left ( CD-AE \right )\\\\As \; \; \; \; AE>CD \;Ther\! f\! ore \;BC<0
Which is not possible. Hence, the postulate is correct

(ii) From Fig (i),
\; \; \; \; \; \; BC=AC \sin \theta,\\ and\: \; \; \; \;CD-AE=AC \sin \theta \\As\; \; \; \; \; \; BC=-\sqrt{\mu_r \epsilon_r }(AE-CD)\\\\ \therefore \; \; \; \; \; \; AC \sin \theta_i =-\sqrt{\epsilon_r\mu_r }AC \sin \theta\\\\or\; \; \; \; \; \; \; \; \frac{\sin \theta_i}{\sin \theta_r}=\sqrt{\epsilon_r\mu_r }\;n
Which proves Snell's law

Question:23

To ensure almost 100 per cent transitivity, photographic lenses are often coated with a thin layer of dielectric material. The refractive index of this material is intermediated between that of (which makes the optical element of the lens). A typically used dielectric film is MgF2 (n = 1.38). What should the thickness of the film be so that at the center of the visible spectrum (5500 Å) there is a maximum transmission

Answer:


IA is an incident ray at point A is such that the incident angle I is formed from air to the film surface.
AR1 and AD are the reflected and refracted rays, respectively. D is the point on which the partial reflection of glass and film interface. CR2 and AR1 are parallel.
\\\mu (AD + CD) - AB\\ AD = AC = \frac{d}{\cos r}\\\\ d \tan r = \frac{AC}{2}\\\\ d = 1000 \AA

Main Subtopics Covered in NCERT Exemplar Class 12 Physics Solutions Chapter 10 Wave Optics

  • Introduction
  • Huygens Principle
  • Refraction and reflection of plane waves using Huygens Principle
  • Refraction of a plane wave
  • Refraction at a rarer medium
  • Reflection of a plane wave by a plane surface
  • The Doppler Effect
  • Coherent and Incoherent Addition of Waves
  • Interference of light waves and Young’s experiment
  • Diffraction
  • The single slit
  • Seeing the single slit diffraction pattern
  • Resolving power of optical instruments
  • The validity of ray optics
  • Polarisation
  • Polarisation by scattering
  • Polarisation by reflection
Pearson | PTE

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

Apply

NCERT Exemplar Class 12 Physics Chapter Wise Links

Important Topics To Cover For Exams From NCERT Exemplar Class 12 Physics Solutions Chapter 10 Wave Optics

· Class 12 Physics NCERT Exemplar solutions chapter 10 provides for the details regarding plane and secondary wavelets, their propagation along with their features. The Huygens Principle is also used to define the refraction and reflection phenomenon of plane waves and also covers the Doppler’s effect.

· NCERT Exemplar solutions for Class 12 Physics chapter 10 also covers important experiments done by Young known as the Single slit experiment and Double slit experiment, which helped derive path difference, constructive interference and destructive interference of waves.

· NCERT Exemplar Class 12 Physics solutions chapter 10 the lesson also covers the concept of coherent and incoherent waves and their interference pattern. This also includes various other important phenomena such as the polarisation of light to transverse waves, instruments used to polarize the light, and polarisation effect of light on reflection and refraction.

· The lesson concludes with the explanation of two other laws known as the Brewester Law and Malu’s law regarding polarisation of light and formation of plane polarised light using methods such as scattering, reflection and double refraction.

NCERT Exemplar Class 12 Solutions

Also, check the NCERT solutions of questions given in book

Also read NCERT Solution subject wise

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

Must read NCERT Notes subject wise

Also Check NCERT Books and NCERT Syllabus here:

Frequently Asked Questions (FAQs)

1. Are these solutions helpful in board exams?

Yes, these solutions of NCERT will be helpful in board exam preparation as one can understand the chapter and topics better.

2. How these solutions can be used?

One can learn the how to solve questions for this chapter in board exam, can also cross check their answers while practicing. 

3. Are these questions solved as per CBSE?

Yes, each and every question is solved as per the CBSE pattern in NCERT exemplar Class 12 Physics solutions chapter 10, which will help in understanding each step separately.

Also Read

Articles

Upcoming School Exams

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

All India Sainik Schools Entrance Examination

Application Date:24 December,2024 - 13 January,2025

Telangana Intermediate 1st Year Examination

Late Fee Application Date:25 December,2024 - 02 January,2025

Telangana State Board of Intermediate Education Examination

Late Fee Application Date:25 December,2024 - 02 January,2025

National Means Cum-Merit Scholarship

Application Date:27 December,2024 - 09 January,2025

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Digital Banking Business Model
 Via State Bank of India
Business Analytics Foundations
 Via PW Skills
Full-Stack Android Development
 Via Masai School
Introduction to Psychology
 Via San Jose State University, San Jose
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?
quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer
Jefferson 25 September,2024
i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

  1. Re-evaluate Your Study Strategies:

    • Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
    • Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
    • Practice Regularly: Consistent practice is key to mastering chemistry.

  2. Consider Professional Help:

    • Tutoring: A tutor can provide personalized guidance and support.
    • Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.

  3. Explore Alternative Options:

    • Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
    • Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.

  4. Focus on NEET 2025 Preparation:

    • Stay Dedicated: Continue your NEET preparation with renewed determination.
    • Utilize Resources: Make use of study materials, online courses, and mock tests.

  5. Seek Support:

    • Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
    • Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.







Read Complete Answer
Kanishka kaushikii 17 September,2024
i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer
Yuvan 30 August,2024
i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer
Ashvadha 12 July,2024
Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer
kumardurgesh1802 10 July,2024
View All

Popular CBSE Class 12th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
CBSE Single Girl Child Scholarship 2024: Registration extended till January 10; eligibility criteria, amount
December 27, 2024 - 03:14 PM IST
CBSE wants international boards reined in; letter to education ministry seeks directions for AIU
December 24, 2024 - 05:54 PM IST
PM Modi's Pariksha Pe Charcha 2025 to be held next month, registrations open till January 14
December 19, 2024 - 07:42 PM IST
CBSE Board Exams 2025: Online portal for availing exemptions by CWSN students opens
December 18, 2024 - 02:57 PM IST
Board Exams: States agree to equivalence; no question paper ‘jumbling’ from next year, says PARAKH CEO
December 12, 2024 - 12:44 PM IST
Board Exam Date 2025 Live: CBSE, ICSE, BSEB, MPBSE Class 10, 12 timetable out; Punjab, Rajasthan schedule soon
December 08, 2024 - 10:34 PM IST
CBSE Board Exams 2025: Guidelines issued for Class 10, 12 practicals
December 03, 2024 - 01:11 PM IST

Stay up-to date with CBSE Class 12th News

Back to top