NCERT Exemplar Class 12 Physics Solutions Chapter 5 Magnetism and Matter

Question:5.2

The magnetic field of Earth can be modelled by that of a point dipole placed at the center of the Earth. The dipole axis makes an angle of $11.3^{\circ}$ with the axis of Earth. At Mumbai, declination is nearly zero.

Then,
A. the declination varies between $11.3^{\circ}$ W to $11.3^{\circ}$ E.
B. the least declination is$0^{\circ}$°.
C. the plane defined by dipole axis and Earth axis passes through Greenwich.
D. declination averaged over Earth must always be negative.

Answer:

The answer is the option (A)

Earth’s magnetic field is similar to a magnetic dipole and we can simulate the nature of Earth’s magnetic field by assuming a dipole at the center of Earth. The axis of the dipole is at an angle of $11.3^{\circ}$with respect to the axis of rotation.

Question:5.3

In a permanent magnet at room temperature
A. magnetic moment of each molecule is zero.
B. the individual molecules have a non-zero magnetic moment which is all perfectly aligned.
C. domains are partially aligned.
D. domains are all perfectly aligned

Answer:

Question:5.4

Consider the two idealized systems: (i) a parallel plate capacitor with large plates and small separation and (ii) a long solenoid of length L >> R, the radius of the cross-section. In (i) E is ideally treated as a constant between plates and zero outside. In (ii) the magnetic field is constant inside the solenoid and zero outside. These idealized assumptions, however, contradict fundamental laws as below:

A. case (i) contradicts Gauss’s Law for electrostatic fields.
B. case (ii) contradicts Gauss’s Law for magnetic fields.
C. case (i) agrees with $\int E.dl=0$
D. case (ii) contradicts $\int H.dl=I_{en}$

Answer:

Question:5.5

A paramagnetic sample shows a net magnetization of 8 Am–1 when placed in an external magnetic field of 0.6T at a temperature of 4K. When the same sample is placed in an external magnetic field of 0.2 T at a temperature of 16K, the magnetization will be
A. $\frac{32}{3}Am^{-1}$
B. $\frac{2}{3}Am^{-1}$
C. $6Am^{-1}$
D. $2.4Am^{-1}$

Answer:

The answer is the option (B)

As Curie law explains, we can deduce a formula for the relation between magnetic field induction, temperature and magnetisation.

$
\begin{array}{ll}
\text { i.e., } I \text { (magnetisation) } \propto \frac{B \text { (magnetic field induction) }}{t \text { (temperature in kelvin) }} \\
\Rightarrow \frac{I_2}{I_1}=\frac{B_2}{B_1} \times \frac{t_1}{t_2}
\end{array}
$

here

$
\begin{aligned}
I_1 & =8 \mathrm{Am}^{-1} \\
B_1 & =0.6 \mathrm{~T}, t_1=4 \mathrm{~K} \\
B_2 & =0.2 \mathrm{~T}, t_2=16 \mathrm{~K} \\
I_2 & =? \\
\frac{0.2}{0.6} \times \frac{4}{16} & =\frac{I_2}{8} \\
I_2 & =8 \times \frac{1}{12}=\frac{2}{3} \mathrm{Am}^{-1}
\end{aligned}
$

Question:5.7

The primary origin(s) of magnetism lies in
A. atomic currents.
B. Pauli exclusion principle.
C. polar nature of molecules.
D. intrinsic spin of the electron.

Answer:

Question:5.8

A long solenoid has 1000 turns per meter and carries a current of 1 A. It has a soft iron core of $\mu _{r}=1000$. The core is heated beyond the Curie temperature, $T_c$.
A. The H field in the solenoid is (nearly) unchanged, but the B field decreases drastically.
B. The H and B fields in the solenoid are nearly unchanged.
C. The magnetization in the core reverses direction.
D. The magnetization in the core diminishes by a factor of about 10⁸

Answer:

Question:5.9

The essential difference between electrostatic shielding by a conducting shell and magnetostatic shielding is due to
A. electrostatic field lines can end on charges and conductors have free charges.
B. lines of B can also end, but conductors cannot end them.
C. lines of B cannot end on any material, and perfect shielding is not possible.
D. shells of high permeability materials can be used to divert lines of B from the interior region.

Answer:

Question:5.10

Let the magnetic field on Earth be modelled by that of a point magnetic dipole at the center of Earth. The angle of dip at a point on the geographical equator
A. is always zero.
B. can be zero at specific points.
C. can be positive or negative.
D. is bounded.

Answer:

The correct answer are the options (B,C,D)
Earth’s magnetic dipole is at an angle of $11.3^{\circ}$ with respect to the axis of rotation. However, the South of dipole is near the Geographical North Pole and North of dipole is near the Geographical South Pole. Though the magnetic field created by this dipole will be zero at its equatorial plane (not the equator), it will pass the equator at two points, where the magnetic field will be zero. Angle of dip flips in sign at the equatorial plane (+ve on one side and -ve on the other)

Question:5.12

A permanent magnet in the shape of a thin cylinder of length 10 cm has $M = 10^{6}\frac{A}{m}$ Calculate the magnetization current I_M.

Answer:

Question:5.13

Explain quantitatively the order of magnitude difference between the diamagnetic susceptibility of $N_{2}(5 \times 10^{-9})$ (at STP) and $Cu ( 10^{-5})$

Answer:

Question:5.14

From molecular viewpoint, discuss the temperature dependence of susceptibility for diamagnetism, paramagnetism and ferromagnetism.

Answer:

Question:5.15

A ball of superconducting material is dipped in liquid nitrogen and placed near a bar magnet. (i) In which direction will it move? (ii) What will be the direction of its magnetic moment?

Answer:

Both liquid nitrogen and the superconducting material are diamagnetic in nature. This does not change even when the superconducting material is dipped into liquid nitrogen. In presence of an external magnetic field, superconducting material will be repelled opposite to the direction of the magnetic field.

Question:5.17

Three identical bar magnets are riveted together at center in the same plane as shown in Figure. This system is placed at rest in a slowly varying magnetic field. It is found that the system of magnets does not show any motion. The north-south poles of one magnet is shown in the Figure. Determine the poles of the remaining two.

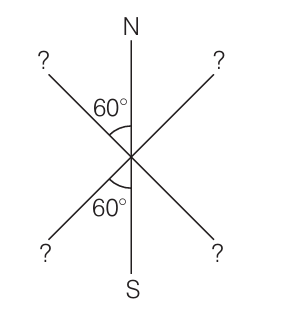
Answer:

Question:5.18

Suppose we want to verify the analogy between electrostatic and magnetostatic by an explicit experiment. Consider the motion of (i) electric dipole p in an electrostatic field E and (ii) magnetic dipole m in a magnetic field B. Write down a set of conditions on E, B, p, m so that the two motions are verified to be identical. (Assume identical initial conditions)

Answer:

Question:5.19

A bar magnet of magnetic moment m and moment of inertia I (about center, perpendicular to length) is cut into two equal pieces, perpendicular to length. Let T be the period of oscillations of the original magnet about an axis through the mid-point, perpendicular to length, in a magnetic field B. What would be the similar period T’ for each piece?

Answer:

Time period in this type of S.H.M is
$T=2\pi \sqrt{\frac{I}{MB} }$
where, T=time period
I=moment of Inertia
m=mass of magnet
B=magnetic field
$I=\frac{ml^2}{12}$
When the magnet is cut into two equal pieces, perpendicular to length the M.O.I of each piece of magnet about an axis perpendicular to the length passing through its centre is
$I'=\frac{m/2}{12}\left (\frac{l}{2} \right )^2\times =\frac{ml^2}{12}\times \frac{1}{}8=\frac{I}{}8$
Magnetic dipole moment

$M'=\frac{M}{}2$
Its time period of oscillation is

$T'=\frac{T}{2}$

Question:5.20

Use (i) the Ampere’s law for H and (ii) continuity of lines of B, to conclude that inside a bar magnet, (a) lines of H run from the N pole to S pole, while (b) lines of B must run from the S pole to N pole.

Answer:

Consider a magnetic field line of B through the bar magnet as given in the figure below.

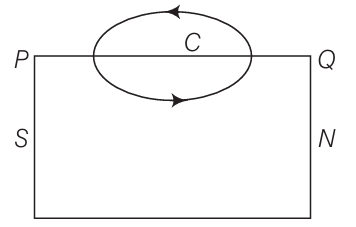
The magnetic field line of $B$ through the bar magnet must be a closed loop.

Let $C$ be the amperian loop. Then,

$
\int_Q^P H \cdot d l=\int_Q^P \frac{B}{m_0} \cdot d l
$

We know that the angle between $\mathbf{B}$ and $\mathbf{d} \mathbf{l}$ is less than $90^{\circ}$ inside the bar magnet. So, it is positive.
i.e.,

$
\int_Q^P H \cdot d l=\int_Q^P \frac{B}{\mu_0} \cdot d l>0
$

Hence, the lines of B must run from south pole(S) to north pole ( $N$ ) inside the bar magnet.
According to Ampere's law,

$
\begin{array}{ll}
\therefore & \oint_{P Q P} \mathrm{H} \cdot \mathrm{dl}=0 \\
\therefore & \oint_{P Q P} \mathrm{H} \cdot \mathrm{dl}=\int_P^Q \mathrm{H} \cdot \mathrm{dl}+\int_Q^P \mathrm{H} \cdot \mathrm{dl}=0 \\
\text { As } & \int_Q^P \mathrm{H} \cdot \mathrm{dl}>0, \mathrm{so}, \int_P^Q \mathrm{H} \cdot \mathrm{dl}<0
\end{array}
$

(i.e., negative)

It will be so if angle between $\mathbf{H}$ and $\mathbf{d l}$ is more than $90^{\circ}$, so that $\cos \theta$ is negative. It means the line of $\mathbf{H}$ must run from $N$-pole to $S$-pole inside the bar magnet.

Question:5.22

What are the dimensions of χ, the magnetic susceptibility? Consider an H-atom. Guess an expression for χ, up to a constant by constructing a quantity of dimensions of χ, out of parameters of the atom: e, m, v, R and μ0. Here, m is the electronic mass, v is electronic velocity, R is Bohr radius. Estimate the number so obtained and compare with the value of $\left | x \right |\sim 10^{5}$ for many solid materials.

Answer:

$X_m=\frac{I}{}H=\frac{\text{Intensity of magnetisation}}{\text{Magnetising force }}$
As I and H both have same units and dimensions, hence χ has no dimensions.
Here, χ is related with e, m, v, R and $\mu _{0}$
From Biot-Savart'slaw,
$dB=\frac{\mu _0}{4\pi} Idl\frac{\sin \theta }{r^2 }$
$\mu _0=\frac{4\pi r^2dB}{Idl\sin \theta }=\frac{4\pi r^2}{Idl \sin\theta }\times \frac{F}{qv \sin \theta }$
Dimensions of $\mu _{0}=\frac{L^2\times [MLT^{-2}]}{[QT^{-1}][L]\times 1\times Q[LT^{-1}]\times 1}=[MLQ^{-2} ]$
where Q is the dimension of charge
As χ is dimensionless, it should have no involvement of charge Q in its dimensional formula.
It will be so if μ0 and e together should have the value $\mu _0e^2$, as e has the dimensions of charge.
Let $X= \mu _0e^2 m^av^bR^c .......i$
where a, b ,c are the power of m,v and R respectively
$[M^0L^0T^0A^0T^0]=[MLA^{-2}T^{-2}]\times [A^2T^2][M]^a\times [LT^{-1}]^b\times [L]^c =[M^{1+a}L^{1+b+c}T^{-b}A^0 ]$
Equating the powers we get 0=1+a
a=-1
0=1+b+c
0=-b
b=0
1+0+c=0
c=-1
Putting values in equation i we get $X=\mu _{0}e^2m^{-1}v^2R^{-1}=\frac{\mu _0e^2}{mR }$
Here, $\mu _0=4\pi \times 10^{-7} Tm A^{-1 }$
$e=1.6\times 10^{-19} C$
$m=9.1\times 10^{-31} kg$
$R=10^{-10}m $

$X=\left (4\pi \times 10^{-7} \right )\times \frac{(1.6\times 10^{-19})^{2}}{9.1\times 10^{-31}\times 10^{-10}}\approx 10^{-4}$

Question:5.23

Assume the dipole model for earth’s magnetic field B which is given by BV = vertical component of magnetic field
$=\frac{\mu _{0}}{ 4 \pi}\frac{2m \cos \theta }{r^{3}}$

B_H = Horizontal component of magnetic field$=\frac{\mu _{0}}{ 4 \pi}\frac{ \sin \theta m }{r^{3}}$
$\theta = 90^{\circ}$– latitude as measured from magnetic equator.
Find loci of points for which (i) B is minimum; (ii) dip angle is zero; and (iii) dip angle is $\pm 45^{\circ}$

Answer:

(c)

$tan \delta =\frac{B_v}{B_H}$

Angle of dip

$\delta =\pm 45^{\circ}$
$\frac{ B_v}{B_H}=tan \pm 45^{\circ}$
$\frac{ B_v}{B_H}=1$
$2 \cot \theta =1$
$\tan \theta =\frac{1}{2}$
$\theta =\tan ^{-1}({\frac{1}{2}})$
Thus, $\theta =\tan ^{-1}({\frac{1}{2}})$ is the locus.

Question:5.24

Consider the plane S formed by the dipole axis and the axis of earth. Let P be the point on the magnetic equator and in S. Let Q be the point of intersection of the geographical and magnetic equators. Obtain the declination and dip angles at P and Q.

Answer:

Question:5.25

There are two current carrying planar coils made each from identical wires of length L. $C_1$ is circular (radius R) and $C_2$ is square (side a). They are so constructed that they have the same frequency of oscillation when they are placed in the same uniform B and carry the same current. Find an in terms of R.

Answer: