NCERT Class 12 Chemistry Chapter 4 Notes Chemical Kinetics- Download PDF Notes

Chemical reactions occur everywhere, all the time. Consider rusting iron or our bodies breaking down food, for example. Some processes, such as burning, occur quickly, whilst others, such as converting carbon into diamonds, take a long time. Chemical Kinetics is the branch of Chemistry that investigates how quickly certain reactions occur. It investigates what influences the rate of reactions and how compounds transform into new products. Understanding the rate of reaction is critical. It has the potential to improve industrial processes, reduce pollution, and potentially contribute to the development of life-saving drugs.

Food preservation is something that we see every day. Fresh fruits and vegetables spoil due to interactions between microbes and oxygen in the air. Storing them in the refrigerator slows down these processes, allowing them to last longer. In medicine, how rapidly a drug dissolves in the body influences its effectiveness. Chemical kinetics notes class 12 also cover the basic equations in Chapter 3. The CBSE Class 12 Chemistry chapter 3 notes do not cover the necessary derivations. These chemical kinetics Class 12 notes also include some solved examples related to mentioned topics. Download the CBSE Notes for chemistry class 12 chapter 3 notes PDF to use offline anywhere.

Also, students can refer,

NCERT Class 12 Chapter 3 Class Notes: Chemical Kinetics

Definition of chemical kinetics : The branch of Chemistry concerned with the study of the rates of chemical reactions, the mechanism by which the reactions proceed, and the factors affecting the rates of the reactions is called Chemical Kinetics.

Rate of a Chemical Reaction

The rate of a reaction can be defined as the change (decrease or increase) in the concentration of a reactant or product in unit time. The rate of a reaction can be given as:

• Average rate

The average rate of reaction can be defined as the change in the concentration of a reactant or product in a definite time interval (Δt). It is denoted by the symbol .

Consider a hypothetical reaction:

Reactant (M) $\to$ Product ( N )

The rate of disappearance of reactant-

$\begin{array}{rl}& r_{av}=\frac{\text{ Decrease in concentration of }M}{\text{ Time taken }}\\ & r_{av}=\frac{-[M]}{\mathrm{\Delta }t}\end{array}$

A minus sign indicates a decrease in concentration.

The rate of appearance of the product-

$\begin{array}{rl}& r_{av}=\frac{\text{ Increase in concentration of }N}{\mathrm{\Delta }t}\\ & r_{av}=\frac{+[N]}{\mathrm{\Delta }t}\end{array}$

• Instantaneous rate

The instantaneous rate of reaction can be defined as the change in the concentration of a reactant or product at a particular instant of time. It is denoted by the symbol $r_{\text{inst }}$..

For an infinitesimally small instant of time $\mathrm{\Delta }t\to 0$,

Therefore,

$r_{inst}=\frac{-\mathrm{d}[M]}{\mathrm{d}t}=\frac{\mathrm{d}[P]}{\mathrm{d}t}$

• The overall rate of reaction

For an overall rate of reaction, the rate of disappearance of any of the reactants (or the rate of appearance of products) is divided by their corresponding stoichiometric coefficients.

Such that for a reaction,

$\mathrm{aA}+\mathrm{bB}\to \mathrm{cC}+\mathrm{dD}$

The overall rate is given as:

$\frac{1}{a}\frac{-\mathrm{d}[A]}{\mathrm{d}t}=\frac{1}{b}\frac{-\mathrm{d}[B]}{\mathrm{d}t}=\frac{1}{c}\frac{+\mathrm{d}[C]}{\mathrm{d}t}=\frac{1}{d}\frac{+\mathrm{d}[D]}{\mathrm{d}t}$

Or

$\frac{-[A]}{a\mathrm{\Delta }t}=\frac{-[B]}{b\mathrm{\Delta }t}=\frac{+[C]}{c\mathrm{\Delta }t}=\frac{+[D]}{d\mathrm{\Delta }t}$

Factors Influencing Rate of a Reaction

Major factors that influence the rate of reaction are:

• Concentration of reactants

• Temperature

• Catalyst

• Rate Law

Concentration of reactants

When the rate of reaction is represented in terms of the concentration of the reactants is known as rate law. It is also known as the rate equation or rate expression.

Consider the following reaction:

$\mathrm{aA}+\mathrm{bB}\to \mathrm{cC}+\mathrm{dD}$

The rate law for this reaction is:

Rate $\propto [A{]}^x[B{]}^y$

Where x and y represent order w.r.t to A and B and may or may not be equal to a and b.

The differential form of the rate law is:

$\frac{-\mathrm{d}[R]}{\mathrm{d}t}=k[A{]}^x[B{]}^y$

• Order of a reaction

The order of the chemical reaction is the summation of powers raised to the concentration of the reactants in the rate law.

For a reaction,

$\mathrm{aA}+\mathrm{bB}\to \mathrm{cC}+\mathrm{dD}$

The rate law is:

Rate $\propto [A{]}^x[B{]}^y$

Therefore, the order of the reaction is x+y.

The order of a reaction can be 0,1,2,3 and fraction.

Order can never be a negative number.

• Units of rate constant

Molecularity of a reaction:

The sum total of species reacting or (molecules, atoms, ions) taking part in a chemical reaction is called the molecularity of a reaction.

The reaction can be unimolecular when one reacting species yields product(s).

The reaction can be bimolecular when two reacting species are involved.

The reaction can be trimolecular when three reacting species are involved.

Integrated rate Equations

• Zero-order reactions

Consider the reaction,

A → P

The rate law of this reaction is given by:

Rate = k[A]₀

On integrating the above equation we get,

$[A{]}_t=[A{]}_0-kt$

The graph of the above equation can be plotted as:

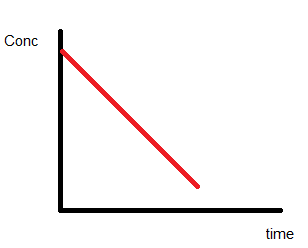
• First-order reaction

Consider the reaction,

A → P

The rate law of this reaction is given by:

Rate = k[A]

On integrating the above equation we get,

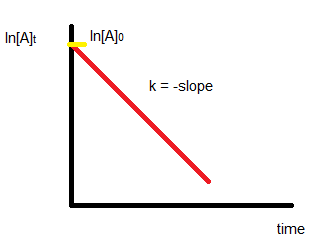
$\ln \left(\frac{[A{]}_0}{[A{]}_t}\right)=kt$

The exponential form of a first-order reaction is given as:

$[A{]}_t=[A{]}_0{e}^{-kt}$

The following equation can be used to plot graphs of first-order reactions:

$k=\frac{1}{t}\ln \left(\frac{[A{]}_0}{[A{]}_t}\right)$

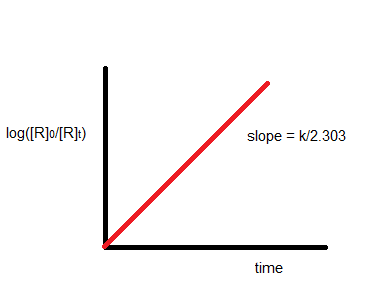
$\log \frac{[A{]}_0}{[A{]}_t}=\frac{kt}{2.303}$

The half-life of a reaction:

The time in which the concentration of a reactant is decreased to one-half of its initial concentration is known as the half-life of a reaction. Half-life is represented as t_1/2.

• For zero-order reactions

$t_{1/2}=\frac{[A{]}_0}{2k}$

• For first-order reactions

$t_{1/2}=\frac{0.693}{k}$

Note that for zero-order reaction $t_{1/2}\propto [A{]}_0$. For the first-order reaction, $t_{1/2}$ is independent of $[A{]}_0$.

Pseudo-first-order reactions:

The reactions in which the actual order is different from the expected rate order predicted using rate law are called pseudo-first-order reactions.

${\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5+{\mathrm{H}}_2\mathrm{O}\stackrel{{\mathrm{H}}^{+}}{\to }{\mathrm{CH}}_3\mathrm{COOH}+{\mathrm{C}}_2{\mathrm{H}}_5\mathrm{OH}$

The rate law of the reaction:

Rate $=k^{\prime }\left[{\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5\right]\left[{\mathrm{H}}_2\mathrm{O}\right]$

Expected order = 2

The concentration of water does not get altered much during the reaction as it is in excess and can be considered constant.

Rate $=k\left[{\mathrm{CH}}_3{\mathrm{COOC}}_2{\mathrm{H}}_5\right]$

Actual order = 1

Therefore, the reaction behaves as a first-order reaction, and such reactions are called pseudo-first-order reactions.

Temperature Dependence of the Rate of a Reaction

The fact that the rate of a chemical reaction is dependent on temperature can be explained by the Arrhenius equation.

The mathematical form of the Arrhenius equation is given below:

$k=A{e}^{-Ea/RT}$

where A is the Arrhenius factor / the frequency factor / the pre-exponential factor.

According to Arrhenius, a reaction can take place only when two (or more) molecules collide to form an unstable intermediate. This intermediate exists for a very short time and then breaks up to form product(s).

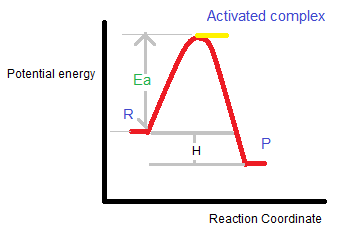
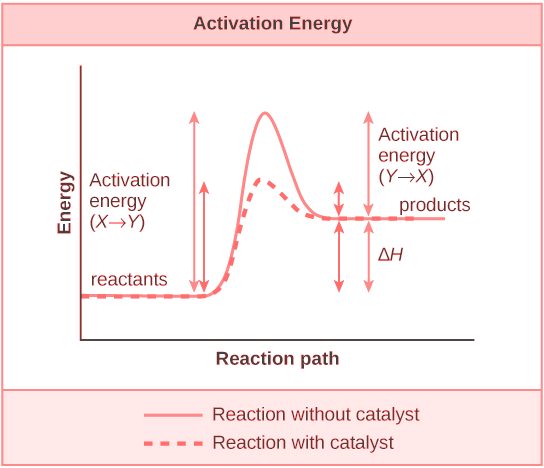
The activation energy ($E_a$) is the mandatory energy required to produce the intermediate activated complex (C). The reaction coordinate depicts the energy change profile when reactants change into products.

The minimum energy which the colliding molecules required to collide effectively is called threshold energy.

Threshold energy = Activation energy + Energy of the reactants

The rate of reaction depends on the temperature as it is found that with the rise in temperature by 10°, the rate constant is nearly doubled.

Temperature coeff icient $=\frac{(\text{ Rate constant at }T+{10}^{\circ })}{\left(\text{ Rate constant at }{T}^{\circ }\right)}$

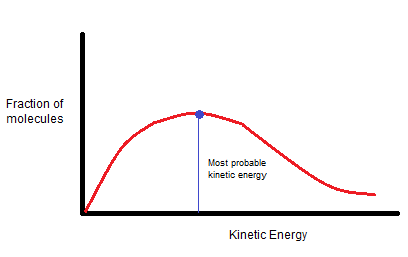
At a particular temperature, the fractions of molecules are plotted against corresponding kinetic energies, a graph given below is obtained.

The peak of the curve represents the kinetic energy possessed by the maximum fraction of molecules and is called the most probable kinetic energy.

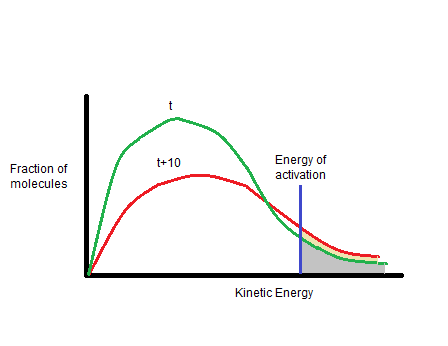
Here, the yellow area shows the fraction of additional molecules which react at t+10 while the grey area shows the fraction of molecules reacting at t.

Taking ln on both sides of the following equation:

$\begin{array}{rl}& k=A{e}^{-Ea/RT}\\ & \ln (k)=\frac{-E_a}{RT}+\ln (A)\end{array}$

Arrhenius equation for two different temperatures can be modified as:

$\log \frac{k_2}{k_1}=\frac{E_a}{RT}\frac{[T_2-T_1]}{T_1{T}_2}$

Effect of Catalyst:

• A catalyst is a substance that alters or changes the rate of a reaction without undergoing any permanent chemical change.

• According to intermediate complex theory, a catalyst forms temporary bonds with the reactants, forming an intermediate complex. This is how a catalyst participates in a chemical reaction.

• The catalyst reduces the energy difference known as activation energy between products and reactants which in turn lowers the potential energy barrier.

• A catalyst catalyses to the same extent the forward as well as the backward reactions so that the equilibrium state remains same but equilibrium is reached faster.

Collision Theory of Chemical Reactions

• According to the collision theory of chemical reactions, the reactant molecules are supposed as hard spheres, and the reaction takes place when molecules collide with each other.

$A+B\to$ Products

• The collision frequency (Z) can be defined as the number of collisions per second per unit volume of the reaction mixture.
• Activation energy also affects the rate of chemical reactions.
• Only effective collisions lead to the formation of products.
• The proper orientation of reactant molecules in space leads to bond formation whereas due to improper orientation no products are formed.
• The factor for proper orientation during effective collisions is called the probability or steric factor (P).

$k=P{Z}_{AB}{e}^{-E_a/RT}$

Chapter-Wise NCERT Class 12 Notes Chemistry

Significance of NCERT Class 12 Chemistry Chapter 3 Notes

Chemical kinetics Class 12 notes will be helpful to revise the chapter and get an idea about the main topics covered in the chapter. Also, this NCERT Class 12 Chemistry chapter 3 notes are useful to cover the main topics of Class 12 CBSE Chemistry Syllabus and also for competitive exams like VITEEE, BITSAT, JEE Main, NEET, etc. Class 12 Chemistry chapter 3 notes PDF download can be used to prepare in offline mode.

Subject Wise NCERT Exemplar Solutions

Subject Wise NCERT Solutions