Class 12 Chemistry notes are concise, well-organised study materials that summarise all the important concepts, formulas, reactions, and definitions from the Class 12 Chemistry syllabus. They help students revise topics quickly and understand complex concepts in a simplified way.
NCERT Class 12 Chemistry Chapter 3 Notes Electrochemistry - Download PDF
Have you ever wondered why metals corrode over time or how a battery powers your phone? What causes a chemical reaction to produce electricity? NCERT Notes for Class 12 Chemistry Chapter 2 Electrochemistry answers all these questions that deal with the relationship between electrical energy and chemical reactions. It forms the basis that is going to help students understand complex topics. In our daily lives, we often use batteries in Smartphones and electric vehicles for their charging. This phenomenon is based on Electrochemistry. Many industries depend on Electrochemistry for the refining of metals, wastewater treatment, and impurity removal.
This Story also Contains
- NCERT Notes for Class 12 Chemistry Chapter 2 Electrochemistry: Download PDF
- NCERT Notes for Class 12 Chapter 2 Electrochemistry
- NCERT Chapter 2 Electrochemistry Previous Year Questions and Answers
- How to Master Class 12 Chemistry Chapter 2 Electrochemistry
- NCERT Class 12 Notes Chapter-Wise
- NCERT Solutions for Class 12 Chemistry
- NCERT Exemplar Solutions Class 12 Subject-Wise
The NCERT Notes for Class 12 will be helpful for a quick revision of topics. These electrochemistry class 12 ncert notes are designed by our subject experts, which ensures the credibility of the content provided. It contains all the important formulas of electrochemistry. The galvanic cell converts the chemical energy of the spontaneous reaction into electrical energy. Electrochemical principles are widely used in energy storage systems like lead-acid batteries in vehicles, fuel cells, lithium-ion batteries in smartphones, etc. It becomes difficult and time-consuming for students to read the NCERT books point-to-point. So, to solve this problem, we are providing these NCERT notes that cover all the topics and concepts provided in the chapter in a very clear and comprehensive way. These Electrochemistry class 12 notes are also valuable resources for various competitive exams. Also, check the NCERT Solutions for all the chapters.
NCERT Notes for Class 12 Chemistry Chapter 2 Electrochemistry: Download PDF
Students can download the class 12 chemistry chapter 2 electrochemistry notes pdf from the icon given below to make your learning simple and effective. These NCERT Notes for Class 12 Chemistry cover important topics like electrochemical cells, Nernst equation, and batteries, helping in quick revision and exam preparation.
Also read
NCERT Notes for Class 12 Chapter 2 Electrochemistry
These electrochemistry class 12 ncert notes cover a brief outline of topics such as electrochemical cells, Nernst equation, the Gibbs energy of cell reaction, conductivity, Kohlrausch law and its applications, electrolysis, etc. These notes are the best resource for quick revision, also they help build a clear understanding of fundamental principles and their real-life applications, such as batteries and corrosion. Detailed notes of this chapter are given below.
Conductance of Electrolytic Solutions;
Conductance:
Conductance is the measure of the ease with which current flows through a conductor.
The inverse of resistance, R, is called conductance, G:
$G=1 / R$
where ($R=\rho l / A$)
$\mathrm{G}=\mathrm{A} / \mathrm{\rho l}$
G = KA/l
Where R is resistance, l is length, A is an area of cross-section, ρ (rho) is resistivity, and κ(kappa) is conductivity.
Conductivity:
The inverse of resistivity is called conductivity. The SI units of conductivity are $\mathrm{S} \mathrm{m}^{-1}$, but quite often, κ is expressed in $\mathrm{S} \mathrm{cm}^{-1}$.
κ = 1/ρ
The conductivity of a material in $\mathrm{S} \mathrm{m}^{-1}$ is its conductance when it is 1 m long and its area of cross-section is $1 \mathrm{~m}^2$. It may be noted that 1 $\mathrm{S} \mathrm{cm}^{-1}$.
Molar conductivity:
Molar Conductivity is described as the conducting power produced by the ions by dissolving one mole of electrolyte in a solvent.
Molar conductivity =$\Lambda _{m}=\frac{\kappa }{C}$
Conductivity and molar conductivity-
m= κ×1000/M
Equivalent conductivity-
Equivalent conductivity is defined as the conductivity power of combining ions formed by the dissolution of an electrolyte of one gram equivalent in a solution.
e= κ×1000/Ceq
Measurement of the Conductivity of Ionic Solutions:
We know that accurate measurement of an unknown resistance can be performed on a Wheatstone bridge.
Wheatstone bridge:
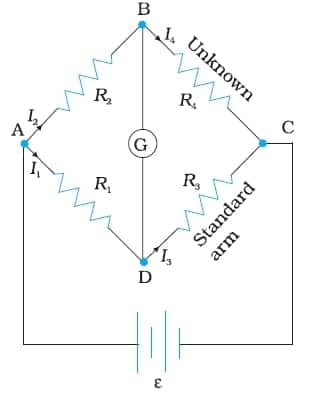
It consists of two resistors, R1 and R3, a variable resistor, R2, and the unknown resistor, R4. The Wheatstone bridge is fed by an oscillator $\varepsilon$ (a source of a.c. power). G is a suitable detector (an electronic device, such as a galvanometer), and the bridge is balanced when no current passes through the detector. Under these conditions:
Unknwon resistance $R_{4}=\frac{R_{2}R_{3}}{R_{1}}$
Once the cell constant and the resistance of the solution in the cell are determined, the conductivity of the solution is given by the equation:
$\kappa$ = cell constant/R =G*/R
Variation of conductivity and molar conductivity with concentration:
Electrolytic conductance decreases with an increase in concentration or increases with an increase in dilution.
Molar conductivity increases with dilution:
The equation of Debye-Huckel-Onsager shows the variation of molar conductivity along with concentration for strong electrolytes.
For strong electrolytes: For strong electrolytes, $\Lambda _{m}$ increases slowly with dilution and can be represented by the equation:
$\Lambda _{m}=\Lambda ^{^{\circ}}_{m} - Ac^{1/2}$
Variation of molar conductivity with concentration for weak electrolytes:
Molar conductivity of weak electrolytes cannot be found for weak electrolytes because the dissociation of weak electrolytes is much lower compared to strong electrolytes.
For weak electrolytes, molar conductivity at infinite dilution can be found using Kohlrausch law.
At any concentration c, if α is the degree of dissociation, then it can be approximated by the ratio of molar conductivity $\Lambda _{m}$ at the concentration c to the limiting molar conductivity $\Lambda ^{^{\circ}}_{m}$. Thus we have:
α = $\Lambda _{m}$/ $\Lambda ^{^{\circ}}_{m}$
Kohlrausch’s Law:
At infinite dilution when ions are completely dissociated, every ion makes its unique contribution to the molar conductivity of the electrolyte, irrespective of the nature of the other ion with which it is associated. Students can also refer to ncert class 12 chemistry chapter 2 electrochemistry notes for practicing questions related to these topics.
Applications of Kohlrausch's Law -
1. Calculation of molar conductance at infinite dilution for weak electrolytes
2. The degree of dissociation of weak electrolytes is calculated as
α = $\Lambda _{m}$/ $\Lambda ^{^{\circ}}_{m}$
3. Calculation of the dissociation constant of weak electrolytes.
$K_{a}=\frac{C\alpha^2}{1-\alpha }$
4. Calculation of the solubility of sparingly soluble salts.
solubility= κ×1000
Electrochemical Cells:
Electrochemical cells are devices that convert chemical energy into electrical energy or vice versa through redox reactions. Students can also refer to NCERT Solutions for Class 12 Chapter 2 Electrochemistry to practise and solve questions from these topics effectively.
Galvanic cells:
Converts the chemical energy of a spontaneous reaction into electrical energy.
Two half cells -
$\mathrm{Cu}^{+2}+2 \mathrm{e}^{-} \rightarrow \mathrm{Cu}_{(\mathrm{s})}($ reduction half cell $)$
$\mathrm{Zn}_{(\mathrm{s})} \rightarrow \mathrm{Zn}^{2+}+2 \mathrm{e}^{-}$(oxidation half cell)
Overall cell reaction-
$\mathrm{Zn}_{(\mathrm{s})}+\mathrm{Cu}^{+2}(\mathrm{aq}) \rightarrow \mathrm{Zn}^{2+}{ }_{(\mathrm{aq})}+\mathrm{Cu}_{(\mathrm{s})}$
Cell potential-
The Potential difference between two electrodes of a Galvanic Cell is called cell potential.
Measurement of Electrode Potential: EMF (Electromotive Force):
Emf Of Cell is the potential difference between the anode and the cathode when no current is drawn through the cell.
$E_{\text {cell }}=E_{\text {right }}-E_{\text {left }}$
Feasibility of a reaction-
$E_{\text {cell }}=E_{\text {right }}-E_{\text {left }}$
Reduction Half-$2 \mathrm{Ag}^{+}(a q)+2 e^{-} \rightarrow 2 \mathrm{Ag}(s)$
Oxidation Half-$\mathrm{Cu}(s) \rightarrow \mathrm{Cu}^{2+}(a q)+2 e^{-}$
For the above reaction, the reaction is feasible if
Ecell =$\mathrm{E}_{\mathrm{Ag}^{+} / \mathrm{Ag}}$ - $\mathrm{E}_{\mathrm{Cu}^{+2} / \mathrm{Cu}}$ is positive.
SHE ( Standard Hydrogen Electrode) is assigned a zero potential to determine the potential of individual half-cells.
It is denoted by $\mathrm{Pt}_{(\mathrm{s})}\left|\mathrm{H}_{2(\mathrm{~g})}\right| \mathrm{H}^{+}{ }_{(\mathrm{aq})}$
Nernst equation:
For reaction-
$M^{n+}+n e^{-} \longrightarrow M$
$E_{M^{n+} / M}=E_{M^{n+} / M}^{\circ}-\frac{2.303 R T}{n F} \log \frac{1}{\left[M^{n+}\right]}$
$E_{M^{n+} / M}=E_{M^{n+} / M}^{\circ}-\frac{0.0591}{n} \log \left[\frac{1}{M^{n+}}\right]$
Applications of the Nernst equation-
1. Determining the cell potential using the Nernst equation-
Equilibrium Constant from Nernst Equation:
For a chemical reaction-
aA+bB→cC+dD
$E_{\text {cell }}=E_0$ cell $-(R T / n F) \ln (Q)$
$
E_{\text {cell }}=E_{\text {cell }}^{\circ}-\frac{0.0591}{n} \log \left(\frac{[C]^c[D]^d}{[A]^a[B]^b}\right)
$
This is the Nernst equation at 298 K, where:
$E_{\text {cell }}$ is the cell potential under non-standard conditions
$E_{\text {cell }}^{\circ}$ is the standard cell potential
$n$ is the number of moles of electrons transferred
$[A],[B],[C],[D]$ are concentrations of the respective species
$a, b, c, d$ are the stoichiometric coefficients in the balanced redox equation.
2. Determination of the concentration of a solution of a half-cell
Using the Nernst Equation, the concentration of the unknown species can be found.
3. To find the equilibrium constant using the Nernst equation-
At equilibrium, the Nernst equation takes the form of –
$\mathrm{E}^{\circ}$ cell=2.303 (RT/nF) $\log (\mathrm{K})$
Electrochemical Cell and Gibbs Energy of the Reaction:
$\Delta_{\mathrm{r}} \mathrm{G}=-\mathrm{nFEcell}$
This equation can help to predict the feasibility of the reaction.
Electrolysis- The process in which chemical changes take place due to the passage of current.
Faraday’s Law of electrolysis:
There are two Faraday’s Laws Of Electrolysis, Faraday’s first law of electrolysis says that the quantity of substance deposited at the electrode is in direct proportion to the amount the electricity passed through the solution.
$w \propto Z Q$
where w is the gram of substance deposited on passing Q coulombs of electricity if a current of 1 ampere is passed for t seconds.
Faraday’s second law of electrolysis- It says that when an equal amount of electricity is passed through different solutions lined up in series, the mass of the substance deposited at the electrodes is in direct proportion to the equivalent weight. Students can also download these electrochemistry class 12 ncert notes pdf to study offline anytime and anywhere.
Weight of Cu deposited = Weight of Ag deposited
= Eq. wt. of Cu = Eq. wt. of Ag
Batteries:
Primary batteries
1. Dry cells- Found in torches, flashlights, calculators, tape recorders, and many other devices.
Reactions occurring at the electrode are-
Anode
$\mathrm{Zn} \rightarrow \mathrm{Zn}^{+2}+2 \mathrm{e}^{-}$
Cathode
$2 \mathrm{NH}_4^{+}(\mathrm{aq})+2 \mathrm{MnO}_2+2 \mathrm{e}^{-} \rightarrow \mathrm{Zn}^{+2}+2 \mathrm{MnOOH}+2 \mathrm{NH}_3$
Overall-
$\mathrm{Zn}+2 \mathrm{NH}_4^{+}(\mathrm{aq})+2 \mathrm{MnO}_2+\mathrm{Zn}^{+2}+2 \mathrm{MnOOH}+2 \mathrm{NH}_3$
2. Mercury cell-
Found in electrical circuits.
Reactions occurring at the electrodes are-
Anode-
$\mathrm{ZnHg}+2 \mathrm{OH}^{-} \rightarrow \mathrm{ZnO}+\mathrm{H}_2 \mathrm{O}+2 \mathrm{e}^{-}$
Cathode-
$\mathrm{HgO}_{(\mathrm{s})}+\mathrm{H}_2 \mathrm{O}+2 \mathrm{e}^{-} \rightarrow \mathrm{Hg}+2 \mathrm{OH}^{-}$
Overall-
$\mathrm{ZnHg}+\mathrm{HgO} \rightarrow \mathrm{ZnO}+2 \mathrm{OH}^{-}$
Secondary batteries:
1. Lead storage batteries-
Battery used in automobiles.
Reactions taking place at electrodes-
Anode-
$\mathrm{PbS}+\mathrm{SO}_4{ }^{2-} \rightarrow \mathrm{PbSO}_4+2 \mathrm{e}^{-}$
Cathode-
$\mathrm{PbO}_2(\mathrm{~s})+\mathrm{SO}_4^{2-}+4 \mathrm{H}^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{PbSO}_4+2 \mathrm{H}_2 \mathrm{O}$
Overall-
$\mathrm{Pb}+\mathrm{PbO}_2+2 \mathrm{H}_2 \mathrm{SO}_4 \rightarrow 2 \mathrm{PbSO}_4+2 \mathrm{H}_2 \mathrm{O}$
2. Nickel-cadmium storage cell-
Has a longer life than the lead storage battery.
Reactions occurring at electrodes-
Anode-
$\mathrm{Cd}+2 \mathrm{OH}^{-} \rightarrow \mathrm{CdO}+\mathrm{H}_2 \mathrm{O}+2 \mathrm{e}^{-}$
Cathode−
$2 \mathrm{Ni}(\mathrm{OH})_3+2 \mathrm{e}^{-} \rightarrow 2 \mathrm{Ni}(\mathrm{OH})_2+2 \mathrm{OH}^{-}$
Overall-
$\mathrm{Cd}+2 \mathrm{Ni}(\mathrm{OH})_3 \rightarrow \mathrm{CdO}+2 \mathrm{Ni}(\mathrm{OH})_2+\mathrm{H}_2 \mathrm{O}$
Fuel Cells-
- Features
- Reactants are supplied continuously.
- The energy of Combustion of fuels such as H2, CO, CH4, etc. is converted to electrical energy.
- Reactions taking place at electrodes-
Anode-
$2\left[\mathrm{H}_2+2 \mathrm{OH}^{-}(\mathrm{aq}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}+2 \mathrm{e}^{-}\right]$
Cathode-
$\mathrm{O}_2+2 \mathrm{H}_2 \mathrm{O}+4 \mathrm{e}^{-} \rightarrow 4 \mathrm{OH}^{-}(\mathrm{aq})$
Overall-
$2 \mathrm{H}_{2(\mathrm{~g})}+\mathrm{O}_2 \rightarrow 2 \mathrm{H}_2 \mathrm{O}$
Corrosion:
Deterioration of metal over time due to its reaction with air and water.
Except gold, platinum, and palladium all other metals undergo corrosion.
Rusting of iron-
At anode-
$\left[\mathrm{Fe} \rightarrow \mathrm{Fe}^{2+}{ }_{(\mathrm{aq})}+2 \mathrm{e}^{-}\right] \times 2$
At cathode-
$4 \mathrm{H}^{+}+\mathrm{O}_2+4 \mathrm{e}^{-} \rightarrow 2 \mathrm{H}_2 \mathrm{O}$
Overall reaction-
$2 \mathrm{Fe}+4 \mathrm{H}^{+}+\mathrm{O}_2 \rightarrow 2 \mathrm{Fe}^{+2}{ }_{(\mathrm{aq})}+2 \mathrm{H}_2 \mathrm{O}$
Prevention of corrosion-
- Barrier protection
- Sacrificial protection
- electrical protection
NCERT Chapter 2 Electrochemistry Previous Year Questions and Answers
Given below previous years to help you understand important concepts and exam trends. Practising these will improve your accuracy. To understand these concepts better students can refer class 12 chemistry chapter 2 electrochemistry notes.
Question 1. Give reason: In the experimental determination of electrolytic conductance, Direct Current (DC) is not used.
Answer:
Direct Current (DC) is not used in the experimental determination of electrolytic conductance because it causes electrolysis and polarization at the electrodes.
Explanation:
1. Electrolysis occurs with DC:
Because DC causes continuous movement of ions in one direction, this leads to chemical changes at the electrodes, i.e., electrolysis, which interferes with accurate conductance measurement.
2. Polarization of electrodes:
- Ions accumulate at the electrodes, forming concentration gradients or even gas bubbles (like $\mathrm{H}_2$ or $\mathrm{O}_2$).
- This creates an extra resistance called electrode polarization, which distorts the actual conductance reading.
3. AC prevents these issues:
- Alternating Current (AC) changes direction rapidly, so ions oscillate rather than accumulate.
- This prevents electrolysis and minimizes polarization, allowing accurate and stable measurement of conductance.
DC is avoided because it causes electrolysis and electrode polarization, which interfere with the correct determination of electrolytic conductance. AC is used instead for accurate results.
Question 2. Define the following: Fuel cell
Answer:
A fuel cell is an electrochemical device that converts the chemical energy of a fuel, typically hydrogen, and an oxidizing agent, usually oxygen, directly into electricity through electrochemical reactions.
Unlike batteries, fuel cells can continuously generate electricity as long as they have a supply of fuel and oxidant. They are known for their efficiency and clean operation, producing only electricity, water, and heat when hydrogen is used as the fuel. Fuel cells are used in various applications, including transportation and stationary power generation.
Question 3. The electrical resistance of a column of 0.05 M NaOH solution of area $0.8 \mathrm{~cm}^2$ and length $\mathbf{ 40 } \mathrm{cm}$ is $5 \times 10^3 \mathrm{ohm}$. Calculate its resistivity, conductivity, and molar conductivity.
Answer:
We are given:
- Concentration of NaOH solution: $C=0.05 \mathrm{~mol} / \mathrm{L}$
- Area of cross-section: $A=0.8 \mathrm{~cm}^2$
- Length of solution column: $l=40 \mathrm{~cm}$
- Resistance: $R=5 \times 10^3 \Omega$
We are to calculate:
1. Resistivity ( $\rho$ )
2. Conductivity ( $\kappa$ )
3. Molar conductivity ( ${\Lambda}_m$ )
1. Resistivity ( $\rho$ )
Resistivity is given by:
$
\rho=R \cdot \frac{A}{l}
$
Substitute values:
$
\rho=\left(5 \times 10^3\right) \cdot \frac{0.8}{40}=\left(5 \times 10^3\right) \cdot 2 \times 10^{-2}=100 ~\Omega \cdot\mathrm{cm}
$
2. Conductivity ( $\kappa$ )
$
\kappa=\frac{1}{\rho}=\frac{1}{100}=0.01 \mathrm{~S} \mathrm{cm}^{-1}
$
3. Molar conductivity ( $\Lambda_m$ )
$
\Lambda_m=\frac{\kappa \times 1000}{C}
$
$
\Lambda_m=\frac{0.01 \times 1000}{0.05}=200\mathrm{~S} \mathrm{~cm}^2 \mathrm{~mol}^{-1}
$
Hence, the answer is resistivity is 100 ohm cm, conductivity is 0.01 Scm-1, and molar conductivity is (200 Scm2 mol-1).
How to Master Class 12 Chemistry Chapter 2 Electrochemistry
These electrochemistry class 12 ncert notes help to understand the basic concepts from your NCERT book. Below are some points on how students master chapter 2
- In order to learn the basic concepts of electrochemistry students need to understand the basics like electrochemical cells, galvanic and electrolytic cells.
- Nernst equation to calculate electrode potential under different conditions plays an important role in this chapter. To understand this concept better students must refer to electrochemistry class 12 ncert notes.
- They must revise the concepts like standard electrode potentials, Faraday’s laws, and important constants regularly.
- To understand these chapters students must draw labelled diagrams of cells and flowcharts to simplify complex concepts.
- After that students can solve previous year questions from this chapter.
NCERT Class 12 Notes Chapter-Wise
Besides class 12 chemistry chapter 2 electrochemistry notes students can follow the links given below for NCERT notes for each chapter of class 12:
NCERT Solutions for Class 12 Chemistry
These solutions serve as a comprehensive guide to help students understand complex chemical concepts with ease. They provide step-by-step answers to all textbook questions, enabling students to build a strong foundation for board exams and competitive tests.
NCERT Exemplar Solutions Class 12 Subject-Wise
NCERT exemplar solutions for each subject are given below:
Frequently Asked Questions (FAQs)
Q: What is a Electrochemistry Class 12 Chemistry Chapter 2 CBSE Notes?
A:
Electrochemistry is the study of chemical processes that cause the movement of electrons, resulting in the production or use of electrical energy. In Class 12 CBSE notes, it includes topics like electrochemical cells, redox reactions, electrode potentials, and the Nernst equation.
Q: How electrochemistry ncert notes are prepared?
A:
Electrochemistry NCERT notes are prepared by breaking down the chapter into simple sections, highlighting key concepts, formulas, and definitions. Important diagrams, solved examples, and shortcut tricks are added to make learning easier. They are designed to cover the entire NCERT syllabus while simplifying complex topics for quick revision.
Q: What is a class 12 chemistry note?
A:
Q: Where can I find Chemistry Revision notes for CBSE chemistry Chapter 2?
A:
You can find revision NCERT Notes for Class 12 Chemistry Chapter 2 Electrochemistry on trusted educational websites like Careers360 and popular study platforms. These notes are usually available as free downloadable PDFs for quick and easy revision.
Q: Why is electrochemistry important in chemistry?
A:
Electrochemistry is crucial because it helps us understand how chemical energy can be converted into electrical energy and vice versa. This principle is fundamental in batteries, fuel cells, and electrolysis processes, which have practical applications in various industries and technologies.
Q: How can I effectively study Class 12 NCERT Chemistry Chapter 2 Electrochemistry ?
A:
To effectively study Chapter 2, you can create concise notes from the textbook, solve numerical problems, and review diagrams related to electrochemical cells.
Articles
Upcoming School Exams
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Courses After 12th
Applications for Admissions are open.
This ebook serves as a valuable study guide for NEET 2025 exam.
NEET Previous 10 Year Questions
Get nowThis e-book offers NEET PYQ and serves as an indispensable NEET study material.
JEE Main Important Physics formulas
Get nowAs per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters