NCERT Class 12 Chemistry Chapter 2 Notes - Download PDF

It is the maximum amount of a solute that can be dissolved in a specific amount of solvent at a specific temperature and pressure.
Factors affecting solubility
1. Nature of the Solute - a solute dissolves in a solvent if the intermolecular interactions are similar in the two or we may say like dissolves like.
2. Nature of the Solvent
3. Temperature
4 . Pressure

1.3.1 Solubility of a Solid in a Liquid

When a solid solute is added to the solvent, some solute dissolves and its concentration increases in solution. This process is known as dissolution. Pressure does not have any significant effect on the solubility of solids in liquids. It is so because solids and liquids are highly incompressible and practically remain unaffected by changes in pressure.

Some important terms-

Crystallisation - It is a process in which some solute particles in the solution collide with the solid solute particles and get separated out.

Saturated solution - The solution in which no more solute can be dissolved under the same conditions of temperature and pressure is known as a saturated solution.

Unsaturated solution - The solution in which more solute can be dissolved under the same conditions of temperature and pressure is known as an unsaturated solution.

1.3.2 Solubility of a Gas in a Liquid

Henry’s Law:

Henry was the first to give a quantitative relation between pressure and solubility of a gas in a solvent.

The law states that at a constant temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas present above the surface of the liquid or solution. If the solubility of gas is expressed in terms of its mole fraction in the solution, then it can be said that the mole fraction of gas in the solution is proportional to the partial pressure of the gas over the solution.

Alternatively, the most commonly used form of Henry’s law states that “the partial pressure of the gas in vapour phase (P) is proportional to the mole fraction of the gas (x) in the solution” and is expressed as:

$\mathrm{P}=\mathrm{K}_{\mathrm{H}} \mathrm{x}$

Here, K_H is the Henry’s law constant and has the same units as the units of pressure used in the equation. It can be clearly seen that the plot between partial pressure of the gas versus mole fraction of the gas in solution will be a straight line plot, as shown in the figure given below. These NCERT Class 12 Chemistry Chapter 1 Notes are very helpful whether you are preparing for board exams or competitive exams.

Factors governing the value of K_H:

Different gases have different $\mathrm{K}_{\mathrm{H}}$ values at the same temperature. Also, the same gas has different values of KH at different temperatures, which is shown in the table given below. The factors governing the value of Henry’s constant are given below

1. Nature of gas-solvent interaction

As gas-solvent interactions become stronger, the solubility will increase, keeping the pressure constant and thus the value of $\mathrm{K}_{\mathrm{H}}$ will decrease. For example, HCl has a lower value of Henry’s constant as compared to $\mathrm{O}_2$

2. Temperature:

As the temperature increases, the solubility of the gas decreases and hence, keeping the pressure constant for the same gas, the value of $\mathrm{K}_{\mathrm{H}}$ will increase.

For example, if we take the case of water, then the equilibrium constant of the following physical process will represent the Vapour Pressure of Water (Also sometimes called Aqueous Tension)

$\left.\mathrm{H}_2 \mathrm{O}(\mathrm{l})\right) \rightleftharpoons \mathrm{H}_2 \mathrm{O}(\mathrm{g}), \mathrm{K}_{\mathrm{p}}=\mathrm{P}^{\circ}$

At equilibrium, the rate of vaporisation = the rate of condensation and the equilibrium constant of the above vapour-liquid equilibrium represents the vapour pressure of the liquid.

It depends on the nature of the liquid and temperature. Pure liquid always has a vapour pressure greater than its solution.

Vapour pressure of a liquid increases with an increase in temperature due to an increase in kinetic energy of solvent molecules, that is, an increase in evaporation; however, it is independent of the nature of the vessel. Students can also follow Solutions Class 12 Chemistry Chapter 1 CBSE Notes.

Vapour Pressure of a Solution
When a miscible solute is added to a pure solvent, it results in the formation of a solution. As some molecules of solute will replace the molecules of the solvent from the surface, therefore escaping tendency of solvent molecules decreases. This causes a lowering of vapour pressure.

• The vapour pressure of a solution is less than that of the pure solvent.
• If the vapour pressure of the solvent is P and that of the solution is P_s, then the lowering of V.P = P - P_s.
• Vapour pressure of solution decreases as the surface area occupied by the solvent molecule decreases and density increases.

1.4.1 Vapour Pressure of Liquid-Liquid Solutions

Raoult’s law:

Let us consider a binary solution obtained upon mixing of two volatile liquids A and B. When the solution is taken in a closed vessel, both the components would evaporate and eventually an equilibrium would be established between vapour phase and the liquid phase. The vapour pressure over this solution would depend on the volatility of each of the liquids as well as the relative amount of the liquids present in the solution. French Chemist Raoult gave this quantitative relationship between these parameters.

Statement of Raoult’s law:

For a solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction in the solution.

Let us represent the solvent as "A" and the solute as "B".

Before mixing, vapour pressure of A is $\mathrm{P}_{\mathrm{A}}^o$ and vapour pressure of B is $\mathrm{P}_{\mathrm{B}}^0$..

Now, after mixing of solute and solvent, let the partial pressures of solvent A and solute B be P_A and P_B, respectively

Now, according to Raoult's law, the vapour pressure of liquid A is proportional to the mole fraction of liquid A.

Thus,

$\mathrm{P}_{\mathrm{A}}=\mathrm{K}_{\mathrm{A}} \mathrm{P}_{\mathrm{A}}^{\mathrm{o}}$ and $\mathrm{P}_{\mathrm{B}}=\mathrm{K}_{\mathrm{B}} \mathrm{P}_{\mathrm{B}}^{\mathrm{o}}$

Now, to find the value of K_A and K_B, when we have only liquid A, then the partial pressure of A is equal to $\mathrm{P}_{\mathrm{A}}^o$

Thus, $\mathrm{K}_{\mathrm{A}}=\mathrm{P}_{\mathrm{A}}^{\mathrm{o}}$ And similarly, it can be shown that $\mathrm{K}_{\mathrm{B}}=\mathrm{P}_{\mathrm{B}}^{\mathrm{o}}$.
Thus, we can write:

$
\mathrm{P}_{\mathrm{A}}=\mathrm{P}_{\mathrm{A}}^{\mathrm{o}} \mathrm{X}_{\mathrm{A}} \text { and } \mathrm{P}_{\mathrm{B}}=\mathrm{P}_{\mathrm{B}}^o \mathrm{X}_{\mathrm{B}}
$

Now, according to Dalton's law of partial pressure, we have:
Total pressure $\left(P_T\right)=P_A+P_B$
Thus, the total pressure exerted by the vapors of the solutions can be represented as

$
\left(\mathrm{P}_{\mathrm{T}}\right)=\mathrm{P}_{\mathrm{A}}^{\mathrm{o}} \mathrm{X}_{\mathrm{A}}+\mathrm{P}_{\mathrm{B}}^{\mathrm{o}} \mathrm{X}_{\mathrm{B}}
$

Using these equations, the mole fraction of $A$ and $B$ represented as $Y_A$ and $Y_B$ in the vapor phase can be calculated as given by the equations:

$
\mathrm{Y}_{\mathrm{A}}=\frac{\mathrm{P}_{\mathrm{A}}}{\mathrm{P}_{\mathrm{T}}} \text { and } \mathrm{Y}_{\mathrm{B}}=\frac{\mathrm{P}_{\mathrm{B}}}{\mathrm{P}_{\mathrm{T}}}
$

1.4.2 Raoult’s Law as a special case of Henry’s Law

According to Raoult's law, the vapour pressure of a volatile component in a given solution is given by $p_1=x_1 p_1{ }^0$. In the solution of a gas in a liquid, one of the components is so volatile that it exists as a gas and we have already seen that its solubility is given by Henry's law which states that

$$
p=K_{\mathrm{H}} x .
$$

1.4.3 Vapour Pressure of Solutions of Solids in Liquids

The vapour pressure of a solvent decreases when a non-volatile solute is added to it. In a pure solvent, all surface molecules contribute to the vapour pressure. However, when solute particles are present, they occupy part of the surface, reducing the number of solvent molecules that can escape into the vapour phase. As a result, the vapour pressure of the solution becomes lower than that of the pure solvent at the same temperature.

The extent of this decrease depends on the amount and nature of the solute, not its type. This concept is further supported by Raoult's Law, which states that the partial vapour pressure of each volatile component in a solution is directly proportional to its mole fraction.

1.5 Ideal and Non-Ideal Solutions

The solutions can be ideal and non-ideal based on their behaviour.

1.5.1 Ideal Solutions

The solutions that obey Raoult’s law for the entire range of composition are called Ideal solutions.

In these solutions, the solute-solute and solvent-solvent interactions are almost similar to solute-solvent interactions (A-B = A-A or B-B interactions). Since the existing forces and the newly formed forces are almost identical, there is no enthalpy change in the mixing of these solutions i.e $\Delta H_{\operatorname{mix}}=0$.

There is no change in the volume during the mixing process i.e.$\Delta V_{\operatorname{mix}}=0$. For example, if 1 litre solutions of each of liquid A and B are mixed to form an ideal solution, then the solution obtained has a volume equal to 2 litres.

The entropy of mixing is positive as new interactions are introduced into the solution, which increases the randomness of the system and hence $\Delta S_{\operatorname{mix}}>0$. The mixing process is spontaneous and hence $\Delta G_{\operatorname{mix}}<0$.

These solutions have vapor pressure as predicted by Raoult’s law.

$\begin{aligned} & P_A=P_A^o X_A \\ & P_B=P_B^o X_B \\ & P_T=P_A+P_B\end{aligned}$

1.5.2 Non-ideal Solutions

These solutions have vapour pressure less than that predicted by Raoult’s law for the entire range of composition.

This happens when the new solute-solvent interactions are stronger than the interactions in the pure components. Since the newly formed forces are stronger than the existing forces, heat is liberated. Hence, the enthalpy change in the mixing of these solutions is negative i.e $\Delta H_{\operatorname{mix}}<0$.

The change in the volume during the mixing process is positive i.e.$\Delta V_{\operatorname{mix}}<0$.. For example, if 1 litre solutions each of liquid A and B are mixed, then the solution obtained has a volume lesser than 2 litres.

The entropy of mixing is positive as new interactions are introduced into the solution which increases the randomness of the system and hence, The mixing process is spontaneous and hence $\Delta G_{\operatorname{mix}}>0$.

These solutions have vapour pressure greater than that predicted by Raoult’s law.

$\begin{aligned} & P_A<P_A^o X_A \\ & P_B<P_B^o X_B \\ & P_T=P_A+P_B<P_A^o X_A+P_B^o X_B\end{aligned}$

An azeotropic mixture is a solution of two liquids having a certain composition in which both the gas phase and the liquid phase composition are the same i.e. $X_A=Y_A$ and $X_B=Y_B$. These solutions distil over without changes in composition and hence, these cannot be separated by distillation. These solutions are formed by non-ideal solutions which show a large deviation from ideality.

These solutions boil at one particular temperature like a pure liquid and distil over in the same composition and hence are also referred to as constant boiling mixtures.

Types of Azeotropic Mixtures

It is of the following types:

1. Minimum Boiling Azeotropes

   Non-ideal solutions showing large positive deviation from Raoult's law form minimum boiling azeotropes which boil at temperature lower than boiling point of either of the components 'A' or 'B'.

   In the figure given below, the point M represents the azeotropic composition. At this point, vapour pres sure is maximum and therefore the solution has the lowest boiling point.

   

   e.g., Ethanol water mixture on fractional distillation gives a solution containing approximately 95 % by volume of ethanol. Once this composition is achieved, no further separation occurs.

2. Maximum Boiling Azeotropes

   Non-ideal solutions showing large negative deviation from Raoult's law form maximum boiling azeotropes which boil at temperature higher than the boiling point of either of the components 'A' or 'B'.

   In the figure given below, the point B represents the azeotropic composition. At this point, the vapour pressure is minimum and therefore the solution has the lowest boiling point.

   

   e.g Nitric acid and water is an example of this class of azeotrope. This azeotrope has the approximate composition, 68% nitric acid and 32% water by mass

1.6 Colligative Properties and Determination of Molar Mass

The properties which depend on the number of solute particles irrespective of their nature relative to the total number of particles present in the solution. Such properties are called colligative properties. Four colligative properties are there in our syllabus:
(i) Relative Lowering of Vapour Pressure of Solvent
(ii) Elevation of Boiling Point of Solvent
(iii) Depression in the Freezing Point of Solvent
(iv) Osmosis & Osmotic Pressure of Solution

1.6.1 Relative Lowering of Vapour Pressure

According to Raoult’s Law, the vapour pressure of the solvent in the solution is less than the pure solvent.
The Lowering of vapour pressure depends only on the concentration of solute particles & is independent of their nature.

Let's name the solvent as "A" and the solute as "B". Let the vapour pressure of the pure solvent be represented as $P_A{ }^0$. Now, when the solute is dissolved in the solvent, then the vapour pressure of the solution decreases and is represented as $P_{s .}$.

According to Raoult's law, we know:

$
\mathrm{P}_{\mathrm{s}}=\mathrm{P}_{\mathrm{A}}{ }^0 \mathrm{X}_{\mathrm{A}}
$

Now, the sum of the mole fraction of solvent $X_A$ and solute $X_B$ is equal to 1 .
Thus $X_A+X_B=1$
On putting the value of $\mathrm{X}_{\mathrm{A}}$ in equation (i), we get:

$
\begin{aligned}
& P_S=P_A^o\left[1-X_B\right] \\
& P_S=P_A^o-P_A^o X_B
\end{aligned}
$
Therefore, $\mathrm{P}_{\mathrm{A}}{ }^{\circ} \mathrm{X}_{\mathrm{B}}=\mathrm{P}_{\mathrm{A}}{ }^{\circ}-\mathrm{P}_{\mathrm{S}}$
Thus, it can be said that,

$
\frac{\mathrm{P}_{\mathrm{A}}^{\mathrm{o}}-\mathrm{P}_{\mathrm{S}}}{\mathrm{P}_{\mathrm{A}}^o}=\mathrm{X}_{\mathrm{B}}
$

The RHS in the above expression gives us the 'Relative lowering of vapour pressure and is equal to the mole fraction of the solute.

1.6.2 Elevation of Boiling Point

Boiling Point: It is the temperature of a liquid at which its vapour pressure becomes equal to the atmospheric pressure.

Now, the lowering of the vapour pressure of the solution occurs when the addition of non-volatile solute in the solvent. In order to boil the solution, it is necessary to increase the temperature of the solution above the boiling point of the pure solvent. It means the boiling point of the solution is always higher than the boiling point of the pure solvent. This increase in the boiling point of the solution is called elevation in boiling point $\left(\Delta T_b\right)$

• It is also termed as Ebullioscopy.

• Suppose $\mathrm{T}_{\mathrm{b}}^{\circ}$ and $\mathrm{T}_{\mathrm{b}}$ are the B.P. of pure solvent and solution respectively, then elevation in $\mathrm{B} . \mathrm{P}\left(\Delta \mathrm{T}_{\mathrm{b}}\right)$ is given as $\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{T}_{\mathrm{b}}-\mathrm{T}_{\mathrm{b}}^{\circ}$

$\Delta \mathrm{T}_{\mathrm{b}}$ is directly proportional to the molality of solution

$
\begin{aligned}
& \Delta \mathrm{T}_{\mathrm{b}} \propto \mathrm{~m} \\
& \Delta \mathrm{~T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b}} \mathrm{~m}
\end{aligned}
$

- If molality of the solution is one, then

$
\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b}}
$

- The elevation in B.P. is also given as

$
\Delta \mathrm{T}_{\mathrm{b}}=\mathrm{K}_{\mathrm{b}} \times \frac{\mathrm{w}}{\mathrm{M}} \times \frac{1000}{\mathrm{~W}}
$

- Molecular weight of solute can be found out as follows

$
\mathrm{M}=\frac{\mathrm{K}_{\mathrm{b}} \times \mathrm{w} \times 1000}{\Delta \mathrm{~T}_{\mathrm{b}} \times \mathrm{W}}
$

Here, w = weight of solute

W = weight of solvent
K_b= molal elevation constant or ebullioscopic constant.
M = molar mass of solute

M₁ = molar mass of solvent

The unit of Kb is K kg mol-1.

1.6.3 Depression of Freezing Point

Freezing Point: It is the temperature at which the liquid and the solid form of the same substance are in equilibrium and have the same vapour pressure. A solution freezes when its vapour pressure is equal to the vapour pressure of pure solid solvent. Due to the lower vapour pressure of the solution, the solid form of the solution separates at a lower temperature.

On adding a non-volatile solute to the solvent, the vapour pressure of the solution is less than the solvent and the vapour pressure of the solution becomes equal to the vapour pressure of solid solvent at a lower temperature when compared to the pure solvent and hence the freezing point of decreases.

Suppose $\mathrm{T}_{\mathrm{f}}^0$ and $\mathrm{T}_{\mathrm{f}}$ are the freezing point of pure solvent and solution, respectively. Decrease in freezing point $\Delta T_f$ is given as:

$
\Delta \mathrm{T}_{\mathrm{f}}=\mathrm{T}_{\mathrm{f}}^0-\mathrm{T}_{\mathrm{f}}
$

This is also termed as cryoscopy and depression of freezing point $\left(\Delta T_f\right)$
- For a dilute solution, $\Delta T_f$ is directly proportional to the molality $(\mathrm{m})$ of the solution.

Hence $\Delta \mathrm{T}_{\mathrm{f}} \propto \mathrm{m}$

$
\Delta T_f=K_f m
$

If the molality of the solution is one, then

$
\Delta T_f=K_f
$

$\Delta T_f$ and M can be found out by using these relations.

$
\begin{aligned}
& \Delta T_f=K_f \times \frac{w}{M} \times \frac{1000}{W} \\
& M=\frac{K_f \times w \times 1000}{\Delta T_f \times W}
\end{aligned}
$

Here w = weight of solute
W = weight of solvent
K_f = molal depression constant or cryoscopic constant.
M = molar mass of solute

M1 = molar mass of solvent

1.6.4 Osmosis and Osmotic Pressure

Osmosis: It is the flow of solvent molecules from solution of low concentration to solution of higher concentration when they are separated by a semi-permeable membrane(SPM), the concentration obviously being defined with respect to the solute. Semi-permeable membrane consists of a network of submicroscopic pores or holes. The pore size is such that the smaller solvent molecules can move across the membrane while the movement of larger solute molecules is hindered by the smaller pores of the SPM.

For example, raw mangoes shrivel when pickled in brine (saltwater); wilted flowers revive when placed in freshwater, blood cells collapse when suspended in saline water, etc.

The flow will continue till the equilibrium is attained. This flow of the solvent molecules to the solution side across a semipermeable membrane can be stopped if some extra pressure is applied on the solution. This pressure that just stops the flow of solvent is called the osmotic pressure of the solution. The osmotic pressure is represented by the letter $\Pi$ (Pi).

This is illustrated in the Figure given below. The osmotic pressure of a solution is the excess pressure that must be applied to a solution to prevent osmosis, i.e., to stop the passage of solvent molecules through a semipermeable membrane into the solution.

Osmotic pressure is a colligative property as it depends on the number of solute molecules and not on their identity. For dilute solutions, it has been found experimentally that osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus:

$
\Pi=C R T
$

Here $\Pi$ is the osmotic pressure and $R$ is the gas constant. The above equation can also be written as

$
\Pi=\left(\frac{n_2}{V}\right) R T
$

Here $V$ is the volume of a solution in litres containing $n_2$ moles of solute.
If $\mathrm{w}_2$ grams of solute, of molar mass, $\mathrm{M}_2$ is present in the solution, then $\mathrm{n}_2=\mathrm{w}_2 / \mathrm{M}_2$ and we can write,

$
\begin{aligned}
& \Pi V=\frac{W_2 R T}{M_2} \\
& \text { Thus } M_2=\frac{W_2 R T}{\Pi V}
\end{aligned}
$

Isotonic Solution
Two solutions having the same osmotic pressure at a given temperature are called isotonic solutions. When such solutions are separated by a semipermeable membrane no osmosis occurs between them. For example, the osmotic pressure associated with the fluid inside the blood cell is equivalent to that of 0.9% (mass/volume) sodium chloride solution, called normal saline solution and it is safe to inject intravenously.

Hypertonic Solution
The solution which have higher osmotic pressure is called a hypertonic solution. For example, if we place the cells in a solution containing more than 0.9% (mass/volume) sodium chloride, water will flow out of the cells and they will shrink. Such a solution is called hypertonic. It is a concentrated solution.

Hypotonic Solution
The solution which have lower osmotic pressure is called a hypotonic solution. For example, if the salt concentration is less than 0.9% (mass/volume), the solution is said to be hypotonic. In this case, water will flow into the cells if placed in this solution, and they will swell. It is a diluted solution.

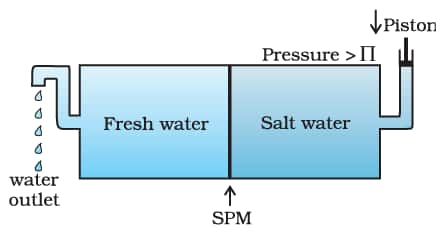
1.6.5 Reverse Osmosis and Water Purification

The direction of osmosis can be reversed if a pressure larger than the osmotic pressure is applied to the solution side. That is, now the pure solvent flows out of the solution through the semi-permeable membrane. This phenomenon is called reverse osmosis and is of great practical utility. Reverse osmosis is used in the desalination of seawater.

The pressure required for reverse osmosis is quite high. A workable porous membrane is a film of cellulose acetate placed over a suitable support.

1.7 Abnormal Molar Masses

The molar mass that is either lower or higher than the expected or normal value is called an abnormal molar mass. In 1880 van’t Hoff introduced a factor i, known as the van’t Hoff factor, to account for the extent of dissociation or association. This factor i is defined as:

$i=\frac{\text { Normal molar mass }}{\text { Abnormal molar mass }}$

$\begin{aligned} & \mathrm{i}=\frac{\text { Observed number of solute particles }}{\text { Number of particles initially taken }} \\ & \mathrm{i}=\frac{\text { Observed value of colligative property }}{\text { Theoretical value of colligative property }}\end{aligned}$