Vector Algebra Class 12 NCERT Solutions (Exercises)
|
Vector Algebra Class 12 Chapter 10 Exercise 10.1
Page number: 342
Total Questions: 5
|
Aakash Repeater Courses
Take Aakash iACST and get instant scholarship on coaching programs.
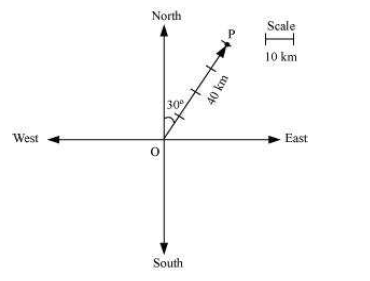
Question: 1 Represent graphically a displacement of 40 km, $30^\circ$ east of north.
Answer:
Represent graphically a displacement of 40 km, $30^\circ$ east of north.
N, S, E, W are all 4 directions: north, south, east, west, respectively.
$\overrightarrow{OP}$ is displacement vector which $\left |\overrightarrow{OP}\right |$ = 40 km.
$\overrightarrow{OP}$ makes an angle of 30 degrees east of north as shown in the figure.
Question: 2 (1) Classify the following measures as scalars and vectors.
10Kg
Answer:
10kg is a scalar quantity as it has only magnitude.
Question: 2 (2) Classify the following measures as scalars and vectors. 2 meters north west
Answer:
This is a vector quantity as it has both magnitude and direction.
Question: 2 (3) Classify the following measures as scalars and vectors. $40^\circ$
Answer:
This is a scalar quantity as it has only magnitude.
Question: 2 (4) Classify the following measures as scalars and vectors. 40 watt
Answer:
This is a scalar quantity as it has only magnitude.
Question: 2 (5) Classify the following measures as scalars and vectors. $10 ^{-19} \: \: coulomb$
Answer:
This is a scalar quantity as it has only magnitude.
Question: 2 (6) Classify the following measures as scalars and vectors. $20 m/s^2$
Answer:
This is a Vector quantity as it has magnitude as well as direction.by looking at the unit, we conclude that measure is acceleration which is a vector.
Question: 3 Classify the following as scalar and vector quantities.
(1) time period
Answer:
This is a scalar quantity as it has only magnitude.
Question: 3 Classify the following as scalar and vector quantities.
(2) distance
Answer:
Distance is a scalar quantity as it has only magnitude.
Question: 3 Classify the following as scalar and vector quantities.
(3) force
Answer:
Force is a vector quantity as it has magnitude and direction.
Question: 3 Classify the following as scalar and vector quantities.
(4) velocity
Answer:
Velocity is a vector quantity as it has both magnitude and direction.
Question: 3 Classify the following as scalar and vector quantities.
(5) work done
Answer:
Work done is a scalar quantity, as it is the product of two vectors.
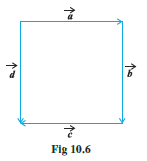
Question: 4 In Fig 10.6 (a square), identify the following vectors.
(1) Coinitial
Answer:
Since vector $\vec{a}$ and vector $\vec{d}$ are starting from the same point, they are coinitial.
Question: 4 In Fig 10.6 (a square), identify the following vectors.
(2) Equal
Answer:
Since Vector $\vec{b}$ and Vector $\vec{d}$ both have the same magnitude and same direction, they are equal.
Question: 4 In Fig 10.6 (a square), identify the following vectors.
(3) Collinear but not equal
Answer:
Since vector $\vec{a}$ and vector $\vec{c}$ have the same magnitude but different direction, they are collinear and not equal.
Question: 5 Answer the following as true or false.
(1) $\vec a$ and $-\vec a$ are collinear.
Answer:
True, $\vec a$ and $-\vec a$ are collinear. they are both parallel to one line, hence they are colinear.
Question: 5 Answer the following as true or false.
(2) Two collinear vectors are always equal in magnitude.
Answer:
False, because colinear means they are parallel to the same line but their magnitude can be anything and hence, this is a false statement.
Question: 5 Answer the following as true or false.
(3) Two vectors having the same magnitude are collinear.
Answer:
False, because any two non-colinear vectors can have the same magnitude.
Question: 5 Answer the following as true or false.
(4) Two collinear vectors having the same magnitude are equal.
Answer:
False, because two collinear vectors with the same magnitude can have opposite directions.
Vector Algebra Class 12 Chapter 10 Exercise 10.2
Page number: 354-355
Total Questions: 19 |
Question: 1 Compute the magnitude of the following vectors:
(1) $\vec a = \hat i + \hat j + \hat k$
Answer:
Here
$\vec a = \hat i + \hat j + \hat k$
Magnitude of $\vec a$
$\vec a=\sqrt{1^2+1^2+1^2}=\sqrt{3}$
Question: 1 Compute the magnitude of the following vectors:
(2) $\vec b = 2 \hat i - 7 \hat j - 3 \hat k$
Answer:
Here,
$\vec b = 2 \hat i - 7 \hat j - 3 \hat k$
Magnitude of $\vec b$
$\left | \vec b \right |=\sqrt{2^2+(-7)^2+(-3)^2}=\sqrt{62}$
Question: 1 Compute the magnitude of the following vectors:
(3) $\vec c = \frac{1}{\sqrt 3 }\hat i + \frac{1}{\sqrt 3 }\hat j -\frac{1}{\sqrt 3 }\hat k$
Answer:
Here,
$\vec c = \frac{1}{\sqrt 3 }\hat i + \frac{1}{\sqrt 3 }\hat j -\frac{1}{\sqrt 3 }\hat k$
Magnitude of $\vec c$
$\left |\vec c \right |=\sqrt{\left ( \frac{1}{\sqrt{3}} \right )^2+\left ( \frac{1}{\sqrt{3}} \right )^2+\left ( \frac{1}{\sqrt{3}} \right )^2}=1$
Question: 2 Write two different vectors having the same magnitude
Answer:
Two different Vectors having the same magnitude are
$\vec a= 3\hat i+6\hat j+9\hat k$
$\vec b= 9\hat i+6\hat j+3\hat k$
The magnitude of both vector
$\left | \vec a \right |=\left | \vec b \right | = \sqrt{9^2+6^2+3^2}=\sqrt{126}$
Question: 3 Write two different vectors having the same direction.
Answer:
Two different vectors having the same direction are:
$\vec a=\hat i+2\hat j+3\hat k$
$\vec b=2\hat i+4\hat j+6\hat k$
Question: 4 Find the values of x and y so that the vectors $2 \hat i + 3 \hat j$ and $x \hat i + y \hat j$ are equal.
Answer:
$2 \hat i + 3 \hat j$ will be equal to $x \hat i + y \hat j$ when their corresponding components are equal.
Hence when,
$x=2$ and $y=3$
Question: 5 Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7).
Answer:
Let point P = (2, 1) and Q = (– 5, 7).
Now,
$\vec {PQ}=(-5-2)\hat i+(7-1)\hat j=-7\hat i +6\hat j$
Hence, scalar components are (-7,6) and the vector is $-7\hat i +6\hat j$
Question: 6 Find the sum of the vectors $\vec a = \hat i - 2 \hat j + \hat k , \vec b = -2 \hat i + 4 \hat j + 5 \hat k \: \: and\: \: \: \vec c = \hat i - 6 \hat j - 7 \hat k$
Answer:
Given,
$\vec a = \hat i - 2 \hat j + \hat k ,\\ \vec b = -2 \hat i + 4 \hat j + 5 \hat k \: \: and\: \: \: \\\vec c = \hat i - 6 \hat j - 7 \hat k$
Now, The sum of the vectors:
$\vec a +\vec b+\vec c = \hat i - 2 \hat j + \hat k + -2 \hat i + 4 \hat j + 5 \hat k + \hat i - 6 \hat j - 7 \hat k$
$\vec a +\vec b+\vec c = (1-2+1)\hat i +(-2+4-6) \hat j + (1+5-7)\hat k$
$\vec a +\vec b+\vec c =-4\hat j-\hat k$
Question: 7 Find the unit vector in the direction of the vector $\vec a = \hat i + \hat j + 2 \hat k$
Answer:
Given
$\vec a = \hat i + \hat j + 2 \hat k$
Magnitude of $\vec a$
$\left |\vec a \right |=\sqrt{1^2+1^2+2^2}=\sqrt{6}$
A unit vector in the direction of $\vec a$
$\vec u = \frac{\hat i}{\left | a \right |} + \frac{\hat j}{\left | a \right |} +\frac{2\hat k}{\left | a \right |} =\frac{\hat i}{\sqrt{6}}+\frac{\hat j}{\sqrt{6}}+\frac{2\hat k}{\sqrt{6}}$
Question: 8 Find the unit vector in the direction of vector $\vec { PQ}$ , where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively.
Answer:
Given P = (1, 2, 3) and Q = (4, 5, 6)
A vector in the direction of PQ
$\vec {PQ}=(4-1)\hat i+(5-2)\hat j +(6-3)\hat k$
$\vec {PQ}=3\hat i+3\hat j +3\hat k$
Magnitude of PQ
$\left | \vec {PQ} \right |=\sqrt{3^2+3^2+3^2}=3\sqrt{3}$
Now, the unit vector in the direction of PQ
$\hat u=\frac{\vec {PQ}}{\left | \vec {PQ} \right |}=\frac{3\hat i+3\hat j+3\hat k}{3\sqrt{3}}$
$\hat u=\frac{\hat i}{\sqrt{3}}+\frac{\hat j}{\sqrt{3}}+\frac{\hat k}{\sqrt{3}}$
Question: 9 For given vectors, $\vec a = 2 \hat i - \hat j + 2 \hat k$ and $\vec b = - \hat i + \hat j - \hat k$ , find the unit vector in the direction of the vector $\vec a + \vec b$ .
Answer:
Given
$\vec a = 2 \hat i - \hat j + 2 \hat k$
$\vec b = - \hat i + \hat j - \hat k$
Now,
$\vec a + \vec b=(2-1)\hat i+(-1+1)\hat j+ (2-1)\hat k$
$\vec a + \vec b=\hat i+\hat k$
Now a unit vector in the direction of $\vec a + \vec b$
$\vec u= \frac{\vec a + \vec b}{\left |\vec a + \vec b \right |}=\frac{\hat i+\hat j}{\sqrt{1^2+1^2}}$
$\vec u= \frac{\hat i}{\sqrt{2}}+\frac{\hat j}{\sqrt{2}}$
Question: 10 Find a vector in the direction of vector $5 \hat i - \hat j + 2 \hat k$ which has magnitude 8 units.
Answer:
Given a vector
$\vec a=5 \hat i - \hat j + 2 \hat k$
the unit vector in the direction of $5 \hat i - \hat j + 2 \hat k$
$\vec u=\frac{5\hat i - \hat j + 2 \hat k}{\sqrt{5^2+(-1)^2+2^2}}=\frac{5\hat i}{\sqrt{30}}-\frac{\hat j}{\sqrt{30}}+\frac{2\hat k}{\sqrt{30}}$
A vector in direction of $5 \hat i - \hat j + 2 \hat k$ and whose magnitude is 8 =
$8\vec u=\frac{40\hat i}{\sqrt{30}}-\frac{8\hat j}{\sqrt{30}}+\frac{16\hat k}{\sqrt{30}}$
Question: 11 Show that the vectors $2 \hat i -3 \hat j + 4 \hat k$ and $- 4 \hat i + 6 \hat j - 8 \hat k$ are collinear.
Answer:
Let
$\vec a =2 \hat i -3 \hat j + 4 \hat k$
$\vec b=- 4 \hat i + 6 \hat j - 8 \hat k$
It can be seen that
$\vec b=- 4 \hat i + 6 \hat j - 8 \hat k=-2(2 \hat i -3 \hat j + 4 \hat k)=-2\vec a$
Hence, here $\vec b=-2\vec a$
As we know
Whenever we have $\vec b=\lambda \vec a$ , the vectors $\vec a$ and $\vec b$ will be colinear.
Here $\lambda =-2$
Hence, vectors $2 \hat i -3 \hat j + 4 \hat k$ and $- 4 \hat i + 6 \hat j - 8 \hat k$ are collinear.
Question:12 Find the direction cosines of the vector $\hat i + 2 \hat j + 3 \hat k$
Answer:
Let $\vec a=\hat i + 2 \hat j + 3 \hat k$
$\left |\vec a \right |=\sqrt{1^2+2^2+3^2}=\sqrt{14}$
Hence direction cosine of $\vec a$ are
$\left ( \frac{1}{\sqrt{14}},\frac{2}{\sqrt{14}} ,\frac{3}{\sqrt{14}}\right )$
Question:13 Find the direction cosines of the vector joining the points A(1, 2, –3) and B(–1, –2, 1), directed from A to B.
Answer:
Given
point A=(1, 2, –3)
point B=(–1, –2, 1)
Vector joining A and B, directed from A to B
$\vec {AB}=(-1-1)\hat i +(-2-2)\hat j+(1-(-3))\hat k$
$\vec {AB}=-2\hat i +-4\hat j+4\hat k$
$\left | \vec {AB} \right |=\sqrt{(-2)^2+(-4)^2+4^2}=\sqrt{36}=6$
Hence, the Direction cosines of vector AB are
$\left ( \frac{-2}{6},\frac{-4}{6},\frac{4}{6} \right )=\left ( \frac{-1}{3},\frac{-2}{3},\frac{2}{3} \right )$
Question: 14 Show that the vector $\hat i + \hat j + \hat k$ is equally inclined to the axes OX, OY and OZ.
Answer:
Let
$\vec a=\hat i + \hat j + \hat k$
$\left | \vec a \right |=\sqrt{1^2+1^2+1^2}=\sqrt{3}$
Hence direction cosines of these vectors are
$\left ( \frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} \right )$
Let $\alpha$ , $\beta$ and $\gamma$ be the angle made by x-axis, y-axis and z- axis respectively
Now, as we know,
$cos\alpha=\frac{1}{\sqrt{3}}$ , $cos\beta=\frac{1}{\sqrt{3}}$ $and\:cos\gamma=\frac{1}{\sqrt{3}}$
Hence, the given vector is equally inclined to the axis OX, OY, and OZ.
Question: 15 (1) Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are $i + 2 j - k$ and $- i + j + k$ respectively, in the ratio 2 : 1 internally
Answer:
As we know
The position vector of the point R which divides the line segment PQ in ratio m:n internally:
$\vec r=\frac{m\vec b+n\vec a}{m+n}$
Here
position vector os P = $\vec a$ = $i + 2 j - k$
the position vector of Q = $\vec b=- i + j + k$
m:n = 2:1
And Hence
$\vec r = \frac{2(-\hat i+\hat j +\hat k)+1(\hat i+2\hat j-\hat k)}{2+1}=\frac{-2\hat i+2\hat j +2\hat k+\hat i+2\hat j-\hat k}{3}$
$\vec r = \frac{-2\hat i+2\hat j +2\hat k+\hat i+2\hat j-\hat k}{3}=\frac{-\hat i+4\hat j+\hat k}{3}$
$\vec r = \frac{-\hat i}{3}+\frac{4\hat j}{3}+\frac{\hat k}{3}$
Question: 15 (2) Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are $\hat i + 2 \hat j - \hat k$ and $- \hat i + \hat j + \hat k$ respectively, in the ratio 2 : 1 externally.
Answer:
As we know
The position vector of the point R, which divides the line segment PQ in ratio m:n externally:
$\vec r=\frac{m\vec b-n\vec a}{m-n}$
Here
position vector os P = $\vec a$ = $i + 2 j - k$
the position vector of Q = $\vec b=- i + j + k$
m:n = 2:1
And Hence
$\vec r = \frac{2(-\hat i+\hat j +\hat k)-1(\hat i+2\hat j-\hat k)}{2-1}=\frac{-2\hat i+2\hat j +2\hat k-\hat i-2\hat j+\hat k}{1}$
$\vec r = -3\hat i +3\hat k$
Question: 16 Find the position vector of the mid point of the vector joining the points P(2, 3, 4) and Q(4, 1, –2).
Answer:
Given
The position vector of point P = $2\hat i+3\hat j +4\hat k$
Position Vector of point Q = $4\hat i+\hat j -2\hat k$
The position vector of R, which divides PQ in half is given by:
$\vec r =\frac{2\hat i+3\hat j +4\hat k+4\hat i+\hat j -2\hat k}{2}$
$\vec r =\frac{6\hat i+4\hat j +2\hat k}{2}=3\hat i+2\hat j +\hat k$
Question:17 Show that the points A, B and C with position vectors, $\vec a = 3 \hat i - 4 \hat j - 4 \hat k , \vec b = 2 \hat i - \hat j + \hat k \: \: and \: \: \: \vec c = \hat i - 3 \hat j - 5 \hat k$ , respectively form the vertices of a right angled triangle.
Answer:
Given
The position vectors of A, B, and C are
$\\\vec a = 3 \hat i - 4 \hat j - 4 \hat k ,\\\vec b = 2 \hat i - \hat j + \hat k \: \: and \\\vec c = \hat i - 3 \hat j - 5 \hat k$
Now,
$\vec {AB}=\vec b-\vec a=-\hat i+3\hat j+5\hat k$
$\vec {BC}=\vec c-\vec b=-\hat i-2\hat j-6\hat k$
$\vec {CA}=\vec a-\vec c=2\hat i-\hat j+\hat k$
$\left | \vec {AB} \right |=\sqrt{(-1)^2+3^2+5^2}=\sqrt{35}$
$\left | \vec {BC} \right |=\sqrt{(-1)^2+(-2)^2+(-6)^2}=\sqrt{41}$
$\left | \vec {CA} \right |=\sqrt{(2)^2+(-1)^2+(1)^2}=\sqrt{6}$
AS we can see
$\left | \vec {BC} \right |^2=\left | \vec {CA} \right |^2+\left | \vec {AB} \right |^2$
Hence, ABC is a right-angle triangle.
Question: 18 In triangle ABC (Fig. 10.18), which of the following is not true:
$A ) \overline{AB}+ \overline{BC}+ \overline{CA} = \vec 0 \\\\ B ) \overline{AB}+ \overline{BC}- \overline{AC} = \vec 0 \\\\ C ) \overline{AB}+ \overline{BC}- \overline{CA} = \vec 0 \\\\ D ) \overline{AB}- \overline{CB}+ \overline{CA} = \vec 0$
Answer:
From triangle law of addition, we have,
$\vec {AB}+\vec {BC}=\vec {AC}$
From here
$\vec {AB}+\vec {BC}-\vec {AC}=0$
Also
$\vec {AB}+\vec {BC}+\vec {CA}=0$
Also
$\vec {AB}-\vec {CB}+\vec {CA}=0$
Hence, options A, B and D are true SO,
Option C is False.
Question: 19 If are two collinear vectors, then which of the following are incorrect:
(A) $\vec b = \lambda \vec a$ for some saclar $\lambda$
(B) $\vec a = \pm \vec b$
(C) the respective components of $\vec a \: \:and \: \: \vec b$ are not proportional
(D) both the vectors $\vec a \: \:and \: \: \vec b$ have same direction, but different magnitudes.
Answer:
If two vectors are collinear, then they have the same direction or are parallel or anti-parallel.
Therefore,
They can be expressed in the form $\vec{b}= \lambda \vec{a}$ where a and b are vectors and $\lambda$ is some scalar quantity.
Therefore, (a) is true.
Now,
(A) $\lambda$ is a scalar quantity so its value may be equal to $\pm 1$
Therefore,
(B) is also true.
C) The vectors $\vec{a}$ and $\vec{b}$ are proportional,
Therefore, (c) is not true.
D) The vectors $\vec{a}$ and $\vec{b}$ can have different magnitudes as well as different directions.
Therefore, (d) is not true.
Therefore, the correct options are (C) and (D).
Vector Algebra Class 12 Chapter 10 Exercise 10.3
Page number: 361-362
Total Questions: 18 |
Question: 1 Find the angle between two vectors $\vec a \: \:and \: \: \vec b$ with magnitudes $\sqrt 3 \: \:and \: \: 2$ , respectively having . $\vec a . \vec b = \sqrt 6$
Answer:
Given
$\left | \vec a \right |=\sqrt{3}$
$\left | \vec b \right |=2$
$\vec a . \vec b = \sqrt 6$
As we know
$\vec a . \vec b = \left | \vec a \right |\left | \vec b \right |cos\theta$
where $\theta$ is the angle between two vectors
So,
$cos\theta =\frac{\vec a.\vec b}{\left | \vec a \right |\left | \vec b \right |}=\frac{\sqrt{6}}{\sqrt{3}×2}=\frac{1}{\sqrt{2}}$
$\theta=\frac{\pi}{4}$
Hence, the angle between the vectors is $\frac{\pi}{4}$.
Question: 2 Find the angle between the vectors $\hat i - 2 \hat j + 3 \hat k \: \:and \: \: 3 \hat i - 2 \hat j + \hat k$
Answer:
Given two vectors
$\vec a=\hat i - 2 \hat j + 3 \hat k \: \:and \: \: \vec b=3 \hat i - 2 \hat j + \hat k$
Now, As we know,
The angle between two vectors $\vec a$ and $\vec b$ is given by
$\theta=cos^{-1}\left ( \frac{\vec a.\vec b}{\left | \vec a \right |\left | \vec b \right |}\right )$
Hence the angle between $\vec a=\hat i - 2 \hat j + 3 \hat k \: \:and \: \: \vec b=3 \hat i - 2 \hat j + \hat k$
⇒ $\theta=cos^{-1}\left ( \frac{(\hat i-2\hat j+3\hat k).(3\hat i-2\hat j+\hat k)}{\left | \hat i-2\hat j+3\hat k \right |\left |3\hat i-2\hat j+\hat k \right |}\right )$
⇒ $\theta=cos^{-1}\left ( \frac{3+4+3}{\sqrt{1^2+(-2)^2+3^3}\sqrt{3^2+(-2)^2+1^2}} \right )$
⇒ $\theta=cos^{-1}\frac{10}{14}$
⇒ $\theta=cos^{-1}\frac{5}{7}$
Question: 3 Find the projection of the vector $\hat i - \hat j$ on the vector $\hat i + \hat j$
Answer:
Let
$\vec a=\hat i - \hat j$
$\vec b=\hat i + \hat j$
Projection of vector $\vec a$ on $\vec b$
$\frac{\vec a.\vec b}{\left | \vec b \right |}=\frac{(\hat i-\hat j)(\hat i+\hat j)}{\left |\hat i+\hat j \right |}=\frac{1-1}{\sqrt{2}}=0$
Hence, the Projection of vector $\vec a$ on $\vec b$ is 0.
Question: 4 Find the projection of the vector $\hat i + 3 \hat j + 7 \hat k$ on the vector $7\hat i - \hat j + 8 \hat k$
Answer:
Let
$\vec a =\hat i + 3 \hat j + 7 \hat k$
$\vec b=7\hat i - \hat j + 8 \hat k$
The projection of $\vec a$ on $\vec b$ is
$\frac{\vec a.\vec b}{\left | \vec b \right |}=\frac{(\hat i+3\hat j+7\hat k)(7\hat i-\hat j+8\hat k)}{\left | 7\hat i-\hat j+8\hat k \right |}=\frac{7-3+56}{\sqrt{7^2+(-1)^2+8^2}}=\frac{60}{\sqrt{114}}$
Hence, projection of vector $\vec a$ on $\vec b$ is $\frac{60}{\sqrt{114}}$.
Question: 5 Show that each of the given three vectors is a unit vector: $\frac{1}{7}( 2 \hat i + 3 \hat j + 6 \hat k ), \frac{1}{7}( 3 \hat i- 6 \hat j + 2 \hat k ), \frac{1}{7}( 6\hat i + 2 \hat j -3\hat k )$ Also, show that they are mutually perpendicular to each other.
Answer:
Given
$\vec a=\frac{1}{7}( 2 \hat i + 3 \hat j + 6 \hat k ), \\\ \vec b =\frac{1}{7}( 3 \hat i- 6 \hat j + 2 \hat k ),\\\vec c = \frac{1}{7}( 6\hat i + 2 \hat j -3\hat k )$
Now magnitude of $\vec a,\vec b \:and\: \vec c$
$\left | \vec a \right |=\frac{1}{7} \sqrt{2^2+3^2+6^2}=\frac{\sqrt{49}}{7}=1$
$\left | \vec b \right |=\frac{1}{7} \sqrt{3^2+(-6)^2+2^2}=\frac{\sqrt{49}}{7}=1$
$\left | \vec c \right |=\frac{1}{7} \sqrt{6^2+2^2+(-3)^2}=\frac{\sqrt{49}}{7}=1$
Hence, they are all unit vectors.
Now,
$\vec a.\vec b=\frac{1}{7}(2\hat i+3\hat j+6\hat k)\frac{1}{7}(3\hat i-6\hat j+2\hat k)=\frac{1}{49}(6-18+12)=0$
$\vec b.\vec c=\frac{1}{7}(3\hat i-6\hat j+2\hat k)\frac{1}{7}(6\hat i+2\hat j-3\hat k)=\frac{1}{49}(18-12-6)=0$
$\vec c.\vec a=\frac{1}{7}(6\hat i+2\hat j-3\hat k)\frac{1}{7}(2\hat i+3\hat j-6\hat k)=\frac{1}{49}(12+6-18)=0$
Hence, all three are mutually perpendicular to each other.
Question: 6 Find $|\vec a| \: \: and\: \:| \vec b |$ , if $( \vec a + \vec b ). ( \vec a - \vec b )=8 \: \:and \: \: |\vec a |\: \:= 8 \: \:|\vec b |$ .
Answer:
Given in the question
$( \vec a + \vec b ). ( \vec a - \vec b )=8$
$\left | \vec a \right |^2-\left | \vec b \right |^2=8$
Since $|\vec a |\: \:= 8 \: \:|\vec b |$
⇒ $\left | \vec {8b} \right |^2-\left | \vec b \right |^2=8$
⇒ $\left | \vec {63b} \right |^2=8$
⇒ $\left | \vec {b} \right |^2=\frac{8}{63}$
⇒ $\left | \vec {b} \right |=\sqrt{\frac{8}{63}}$
So, the answer is
$\left | \vec {a} \right |=8\left | \vec {b} \right |=8\sqrt{\frac{8}{63}}$
Question: 7 Evaluate the product $( 3\vec a - 5 \vec b ). ( 2 \vec a + 7 \vec b )$ .
Answer:
To evaluate the product $( 3\vec a - 5 \vec b ). ( 2 \vec a + 7 \vec b )$
$( 3\vec a - 5 \vec b ). ( 2 \vec a + 7 \vec b )=6\vec a.\vec a+21\vec a.\vec b-10\vec b.\vec a-35\vec b.\vec b$
$=6\vec a.^2+11\vec a.\vec b-35\vec b^2$
$=6\left | \vec a \right |^2+11\vec a.\vec b-35\left | \vec b \right |^2$
Question: 8 Find the magnitude of two vectors $\vec a \: \: and \: \: \vec b$ , having the same magnitude and such that the angle between them is $60 ^\circ$ and their scalar product is 1/2
Answer:
Given two vectors $\vec a \: \: and \: \: \vec b$
$\left | \vec a \right |=\left | \vec b\right |$
$\vec a.\vec b=\frac{1}{2}$
Now Angle between $\vec a \: \: and \: \: \vec b$
$\theta=60^0$
Now, As we know that
$\vec a.\vec b=\left | \vec a \right |\left | \vec b \right |cos\theta$
$\frac{1}{2}=\left | \vec a \right |\left | \vec a \right |cos60^0$
$\left | a \right |^2=1$
Hence, the magnitude of two vectors $\vec a \: \: and \: \: \vec b$
$\left | a \right |=\left | b \right |=1$
Question: 9 Find $|\vec x |$ , if for a unit vector $\vec a , ( \vec x -\vec a ) . ( \vec x + \vec a ) = 12$
Answer:
Given in the question that
$( \vec x -\vec a ) . ( \vec x + \vec a ) = 12$
And we need to find $\left | \vec x \right |$
$\left | \vec x \right |^2-\left | \vec a \right |^2 = 12$
⇒ $\left | \vec x \right |^2-1 = 12$
⇒ $\left | \vec x \right |^2 = 13$
⇒ $\left | \vec x \right | = \sqrt{13}$
So the value of $\left | \vec x \right |$ is $\sqrt{13}$.
Question:10 If $\vec a = 2 \hat i + 2 \hat j + 3 \hat k , \vec b = - \hat i + 2 \hat j + \hat k \: \: and \: \: \vec c = 3 \hat i + \hat j$ are such that $\vec a + \lambda \vec b$ is perpendicular to $\vec c$ , then find the value of $\lambda$
Answer:
Given in the question is
$\vec a = 2 \hat i + 2 \hat j + 3 \hat k , \vec b = - \hat i + 2 \hat j + \hat k \: \: and \: \: \vec c = 3 \hat i + \hat j$
and $\vec a + \lambda \vec b$ is perpendicular to $\vec c$
and we need to find the value of $\lambda$ ,
So the value of $\vec a + \lambda \vec b$ -
$\vec a + \lambda \vec b=2\hat i +2\hat j +3\hat k+\lambda (-\hat i+2\hat j+\hat k)$
$\vec a + \lambda \vec b=(2-\lambda)\hat i +(2+2\lambda)\hat j +(3+\lambda)\hat k$
As $\vec a + \lambda \vec b$ is perpendicular to $\vec c$
$(\vec a + \lambda \vec b).\vec c=0$
⇒ $((2-\lambda)\hat i +(2+2\lambda)\hat j +(3+\lambda)\hat k)(3\hat i+\hat j)=0$
⇒ $3(2-\lambda)+2+2\lambda=0$
⇒ $6-3\lambda+2+2\lambda=0$
⇒ $\lambda=8$
The value of $\lambda=8$.
Question:11 Show that $|\vec a | \vec b + |\vec b | \vec a$ is perpendicular to $|\vec a | \vec b - |\vec b | \vec a$ , for any two nonzero vectors $\vec a \: \: \: and \: \: \vec b$ .
Answer:
Given in the question that -
$\vec a \: \: \: and \: \: \vec b$ are two non-zero vectors
According to the question
$\left ( |\vec a | \vec b + |\vec b | \vec a\right )\left (|\vec a | \vec b - |\vec b | \vec a \right )$
$=|\vec a |^2 |\vec b|^2 - |\vec b |^2 |\vec a|^2+|\vec b||\vec a|\vec a.\vec b-|\vec a||\vec b|\vec b.\vec a=0$
Hence, $|\vec a | \vec b + |\vec b | \vec a$ is perpendicular to $|\vec a | \vec b - |\vec b | \vec a$ .
Question:12 If $\vec a . \vec a = 0 \: \: and \: \: \vec a . \vec b = 0$ , then what can be concluded about the vector $\vec b$ ?
Answer:
Given in the question
$\\\vec a . \vec a = 0 \\|\vec a|^2=0$
$\\|\vec a|=0$
Therefore $\vec a$ is a zero vector. Hence any vector $\vec b$ will satisfy $\vec a . \vec b = 0$
Question: 13 If $\vec a , \vec b , \vec c$ are unit vectors such that $\vec a + \vec b + \vec c = \vec 0$ , find the value of $\vec a . \vec b + \vec b. \vec c + \vec c . \vec a$
Answer:
Given in the question
$\vec a , \vec b , \vec c$ are unit vectors $\Rightarrow |\vec a|=|\vec b|=|\vec c|=1$
and $\vec a + \vec b + \vec c = \vec 0$
and we need to find the value of $\vec a . \vec b + \vec b. \vec c + \vec c . \vec a$
$(\vec a + \vec b + \vec c)^2 = \vec 0$
$\vec a^2 + \vec b^2 + \vec c ^2+2(\vec a . \vec b + \vec b. \vec c + \vec c . \vec a)=0$
$|\vec a|^2 + |\vec b|^2 + |\vec c |^2+2(\vec a . \vec b + \vec b. \vec c + \vec c . \vec a)=0$
$1+1+1+2(\vec a . \vec b + \vec b. \vec c + \vec c . \vec a)=0$
$\vec a . \vec b + \vec b. \vec c + \vec c . \vec a=\frac{-3}{2}$
Answer- the value of $\vec a . \vec b + \vec b. \vec c + \vec c . \vec a$ is $\frac{-3}{2}$
Question: 14 If either vector $\vec a = 0 \: \: or \: \: \vec b = 0 \: \: then \: \: \vec a . \vec b = 0$ . But the converse need not be true. Justify your answer with an example
Answer:
Let
$\vec a=\hat i-2\hat j +3\hat k$
$\vec b=5\hat i+4\hat j +1\hat k$
we see that
$\vec a.\vec b=(\hat i-2\hat j +3\hat k)(5\hat i+4\hat j +1\hat k)=5-8+3=0$
we now observe that
$|\vec a|=\sqrt{1^2+(-2)^2+3^2}=\sqrt{14}$
$|\vec b|=\sqrt{5^2+4^2+1^2}=\sqrt{42}$
Hence, here converse of the given statement is not true.
Question:15 If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find $\angle ABC, [\angle ABC$ is the angle between the vectors $\overline{BA}\: \: and\: \: \overline{BC} ]$.
Answer:
Given points,
A=(1, 2, 3),
B=(–1, 0, 0),
C=(0, 1, 2),
As need to find Angle between $\overline{BA}\: \: and\: \: \overline{BC} ]$
$\vec {BA}=(1-(-1))\hat i+(2-0)\hat j+(3-0)\hat k=2\hat i+2\hat j+3\hat k$
$\vec {BC}=(0-(-1))\hat i+(1-0)\hat j+(2-0)\hat k=\hat i+\hat j+2\hat k$
Hence angle between them;
$\theta=cos^{-1}(\frac{\vec {BA}.\vec {BC}}{\left | \vec {BA} \right |\left | \vec {BC} \right |})$
$\theta=cos^{-1}\frac{2+2+6}{\sqrt{17}\sqrt{6}}$
$\theta=cos^{-1}\frac{10}{\sqrt{102}}$
Answer - Angle between the vectors $\overline{BA}\: \: and\: \: \overline{BC}$ is $\theta=cos^{-1}\frac{10}{\sqrt{102}}$
Question:16 Show that the points A(1, 2, 7), B(2, 6, 3) and C(3, 10, –1) are collinear.
Answer:
Given in the question
A=(1, 2, 7), B=(2, 6, 3) and C(3, 10, –1)
To show that the points A(1, 2, 7), B(2, 6, 3) and C(3, 10, –1) are collinear
$\vec {AB}=(2-1)\hat i+(6-2)\hat j+(3-7)\hat k$
$\vec {AB}=\hat i+4\hat j-4\hat k$
$\vec {BC}=(3-2)\hat i+(10-6)\hat j+(-1-3)\hat k$
$\vec {BC}=\hat i+4\hat j-4\hat k$
$\vec {AC}=(3-1)\hat i+(10-2)\hat j+(-1-7)\hat k$
$\vec {AC}=2\hat i+8\hat j-8\hat k$
$|\vec {AB}|=\sqrt{1^2+4^2+(-4)^2}=\sqrt{33}$
$|\vec {BC}|=\sqrt{1^2+4^2+(-4)^2}=\sqrt{33}$
$|\vec {AC}|=\sqrt{2^2+8^2+(-8)^2}=2\sqrt{33}$
As we see that
$|\vec {AC}|=|\vec {AB}|+|\vec {BC}|$
Hence, points A, B, and C are colinear.
Question: 17 Show that the vectors $2 \hat i - \hat j + \hat k , \hat i - 3 \hat j - 5 \hat k \: \: and \: \: 3 \hat i - 4 \hat j - 4 \hat k$ form the vertices of a right angled triangle.
Answer:
Given the position vectors of A, B, and C are
$2 \hat i - \hat j + \hat k , \hat i - 3 \hat j - 5 \hat k \: \: and \: \: 3 \hat i - 4 \hat j - 4 \hat k$
To show that the vectors $2 \hat i - \hat j + \hat k , \hat i - 3 \hat j - 5 \hat k \: \: and \: \: 3 \hat i - 4 \hat j - 4 \hat k$ form the vertices of a right angled triangle
$\vec {AB}=(1-2)\hat i + (-3-(-1))\hat j+(-5-1)\hat k=-1\hat i -2\hat j-6\hat k$
$\vec {BC}=(3-1)\hat i + (-4-(-3))\hat j+(-4-(-5))\hat k=-2\hat i -\hat j+\hat k$
$\vec {AC}=(3-2)\hat i + (-4-(-1))\hat j+(-4-(1))\hat k=\hat i -3\hat j-5\hat k$
$|\vec {AB}|=\sqrt{(-1)^2+(-2)^2+(-6)^2}=\sqrt{41}$
$|\vec {BC}|=\sqrt{(-2)^2+(-1)^2+(1)^2}=\sqrt{6}$
$|\vec {AC}|=\sqrt{(1)^2+(-3)^2+(-5)^2}=\sqrt{35}$
Here we see that
$|\vec {AC}|^2+|\vec {BC}|^2=|\vec {AB}|^2$
Hence, A, B, and C are the vertices of a right-angle triangle.
Question: 18 If $\vec a$ is a nonzero vector of magnitude ‘a’ and $\lambda$ a nonzero scalar, then $\lambda \vec a$ is unit vector if
$\\A ) \lambda = 1 \\\\ B ) \lambda = -1 \\\\ C ) a = |\lambda | \\\\ D ) a = 1 / |\lambda |$
Answer:
Given $\vec a$ is a nonzero vector of magnitude ‘a’ and $\lambda$ a nonzero scalar
$\lambda \vec a$ is a unit vector when
$|\lambda \vec a|=1$
$|\lambda|| \vec a|=1$
$| \vec a|=\frac{1}{|\lambda|}$
Hence, the correct option is D.
Vector Algebra Class 12 Chapter 10 Exercise 10.4
Page number: 368-369
Total Questions: 12 |
Question:1 Find $|\vec a \times \vec b |,\ if \ \vec a = \hat i - 7 \hat j + 7 \hat k \: \: and \: \: \vec b = 3 \hat i - 2 \hat j + 2 \hat k$.
Answer:
Given in the question,
$\\ \vec a = \hat i - 7 \hat j + 7 \hat k \: \: and \: \: \\\vec b = 3 \hat i - 2 \hat j + 2 \hat k$
and we need to find $|\vec a \times \vec b |$
Now,
$|\vec a \times \vec b | =\begin{vmatrix} \hat i &\hat j &\hat k \\ 1 &-7 &7 \\ 3& -2 &2 \end{vmatrix}$
⇒ $|\vec a \times \vec b | =\hat i(-14+14)-\hat j(2-21)+\hat k(-2+21)$
⇒ $|\vec a \times \vec b | =19\hat j+19\hat k$
So, the value of $|\vec a \times \vec b |$ is $19\hat j+19\hat k$.
Question:2 Find a unit vector perpendicular to each of the vector $\vec a + \vec b \: \: and\: \: \vec a - \vec b$ , where $\vec a = 3 \hat i + 2 \hat j + 2 \hat k \: \:and \: \: \vec b = \hat i + 2 \hat j - 2 \hat k$.
Answer:
Given in the question
$\vec a = 3 \hat i + 2 \hat j + 2 \hat k \: \:and \: \: \vec b = \hat i + 2 \hat j - 2 \hat k$
$\vec a + \vec b =3\hat i +2\hat j+2\hat k+\hat i +2\hat j-2\hat k=4\hat i +4\hat j$
$\vec a - \vec b =3\hat i +2\hat j+2\hat k-\hat i -2\hat j+2\hat k=2\hat i +4\hat k$
Now , A vector which perpendicular to both $\vec a + \vec b \: \: and\: \: \vec a - \vec b$ is $(\vec a + \vec b) \times (\vec a - \vec b)$
$(\vec a + \vec b) \times (\vec a - \vec b)=\begin{vmatrix} \hat i &\hat j &\hat k \\ 4&4 &0 \\ 2& 0& 4 \end{vmatrix}$
⇒ $(\vec a + \vec b) \times (\vec a - \vec b)= \hat i (16-0)-\hat j(16-0)+\hat k(0-8)$
⇒ $(\vec a + \vec b) \times (\vec a - \vec b)= 16\hat i -16\hat j-8\hat k$
And a unit vector in this direction :
$\vec u =\frac{16\hat i-16\hat j-8\hat k}{|16\hat i-16\hat j-8\hat k|}=\frac{16\hat i-16\hat j-8\hat k}{\sqrt{16^2+(-16)^2+(-8)^2}}$
⇒ $\vec u =\frac{16\hat i-16\hat j-8\hat k}{24}=\frac{2}{3}\hat i-\frac{2}{3}\hat j-\frac{1}{3}\hat k$
Hence, Unit vector perpendicular to each of the vector $\vec a + \vec b \: \: and\: \: \vec a - \vec b$ is $\frac{2}{3}\hat i-\frac{2}{3}\hat j-\frac{1}{3}\hat k$.
Question:3 If a unit vector $\vec a$ makes angles $\frac{\pi }{3}$ with $\hat i , \frac{\pi }{4}$ with $\hat j$ and an acute angle $\theta$ with $\hat k$ then find $\theta$ and hence, the components of $\vec a$.
Answer:
Given in the question,
Angle between $\vec a$ and $\hat i$ :
$\alpha =\frac{\pi}{3}$
Angle between $\vec a$ and $\hat j$
$\beta =\frac{\pi}{4}$
Angle with $\vec a$ and $\hat k$ :
$\gamma =\theta$
Now, as we know,
$cos^2\alpha+cos^2\beta+cos^2\gamma=1$
⇒ $cos^2\frac{\pi}{3}+cos^2\frac{\pi }{4}+cos^2\theta=1$
⇒ $\left ( \frac{1}{2} \right )^2+\left ( \frac{1}{\sqrt{2}} \right )^2+cos^2\theta=1$
⇒ $cos^2\theta=\frac{1}{4}$
⇒ $cos\theta=\frac{1}{2}$ (As $\theta$ is acute)
⇒ $\theta=\frac{\pi}{3}$
Now, components of $\vec a$ are:
$\left ( cos\frac{\pi}{3},cos\frac{\pi}{2},cos\frac{\pi}{3} \right )=\left ( \frac{1}{2},\frac{1}{\sqrt{2}},\frac{1}{2} \right )$.
Question:4 Show that $( \vec a - \vec b ) \times (\vec a + \vec b ) = 2 ( \vec a \times \vec b )$
Answer:
To show that $( \vec a - \vec b ) \times (\vec a + \vec b ) = 2 ( \vec a \times \vec b )$
LHS
$( \vec a - \vec b ) \times (\vec a + \vec b )=( \vec a - \vec b ) \times (\vec a)+( \vec a - \vec b ) \times (\vec b)$
⇒ $( \vec a - \vec b ) \times (\vec a + \vec b )= \vec a \times \vec a-\vec b \times\vec a+\vec a \times \vec b-\vec b \times \vec b$
As product of a vector with itself is always Zero,
$( \vec a - \vec b ) \times (\vec a + \vec b )= 0-\vec b \times\vec a+\vec a \times \vec b-0$
As cross product of a and b is equal to negative of cross product of b and a.
$( \vec a - \vec b ) \times (\vec a + \vec b )= \vec a \times\vec b+\vec a \times \vec b$
⇒ $( \vec a - \vec b ) \times (\vec a + \vec b )= 2(\vec a \times\vec b)$ = RHS
LHS is equal to RHS, Hence Proved.
Question:5 Find $\lambda$ and $\mu$ if $( 2 \hat i + 6 \hat j + 27 \hat k ) \times ( \hat i + \lambda j + \mu \hat k ) = \vec 0$
Answer:
Given in the question
$(2 \hat i + 6 \hat j + 27 \hat k ) \times ( \hat i + \lambda j + \mu \hat k ) = \vec 0$
and we need to find values of $\lambda$ and $\mu$.
⇒ $\begin{vmatrix} \hat i &\hat j & \hat k\\ 2& 6&27 \\ 1& \lambda &\mu \end{vmatrix}=0$
⇒ $\hat i (6\mu-27\lambda)-\hat j(2\mu-27)+\hat k(2\lambda-6)=0$
From here we get,
$6\mu-27\lambda=0$
$2\mu-27=0$ ⇒ $\mu=\frac{27}{2}$
$2\lambda -6=0$ ⇒ $\lambda = 3$
From here, the value of $\lambda$ and $\mu$ is
$\lambda = 3 , \: and \: \mu=\frac{27}{2}$.
Question:6 Given that $\vec a . \vec b = 0 \: \:and \: \: \vec a \times \vec b = 0$ and . What can you conclude about the vectors $\vec a \: \:and \: \: \vec b$ ?
Answer:
Given in the question
$\vec a . \vec b = 0$ and $\vec a \times \vec b = 0$
When $\vec a . \vec b = 0$ , either $|\vec a| =0,\:or\: |\vec b|=0,\:or\: \vec a\: and \:\vec b$ are perpendicular to each other.
When $\vec a \times \vec b = 0$ either $|\vec a| =0,\:or\: |\vec b|=0,\:or\: \vec a\: and \:\vec b$ are parallel to each other.
Since two vectors can never be both parallel and perpendicular at the same time,
We conclude that
$|\vec a| =0\:or\: |\vec b|=0$.
Question:7 Let the vectors $\vec a , \vec b , \vec c$ be given as $\vec a_1 \hat i + \vec a_2 \hat j + \vec a_3 \hat k , \vec b_ 1 \hat i + \vec b_ 2 \hat j + \vec b_3 \hat k , \vec c_ 1 \hat i + \vec c_ 2 \hat j + \vec c_ 3 \hat k$ Then show that $\vec a \times ( \vec b + \vec c ) = \vec a \times \vec b + \vec a \times \vec c$
Answer:
Given in the question
$\\\vec a=\vec a_1 \hat i + \vec a_2 \hat j + \vec a_3 \hat k , \\\vec b=\vec b_ 1 \hat i + \vec b_ 2 \hat j + \vec b_3 \hat k , \\\vec c=\vec c_ 1 \hat i + \vec c_ 2 \hat j + \vec c_ 3 \hat k$
We need to show that $\vec a \times ( \vec b + \vec c ) = \vec a \times \vec b + \vec a \times \vec c$
Now, $\vec a \times ( \vec b + \vec c ) =(\vec a_1 \hat i + \vec a_2 \hat j + \vec a_3 \hat k)\times(\vec b_ 1 \hat i + \vec b_ 2 \hat j + \vec b_3 \hat k +\vec c_ 1 \hat i + \vec c_ 2 \hat j + \vec c_ 3 \hat k)$
$=(\vec a_1 \hat i + \vec a_2 \hat j + \vec a_3 \hat k)\times((\vec b_ 1+\vec c_1) \hat i + (\vec b_ 2+\vec c_2) \hat j +( \vec b_3 +\vec c_3)\hat k)$
$=\begin{vmatrix} \hat i &\hat j &\hat k \\ a_1&a_2 &a_3 \\ (b_1+c_1)&(b_2+c_2) &(b_3+c_3) \end{vmatrix}$
$=\hat i(a_2(b_3+c_3)-a_3(b_2+c_2))-\hat j(a_1(b_3+c_3)- a_3(b_1+c_1))+\hat k (a_1(b_2+c_2)-a_2(a_1(b_2+c_3)))$
$=\hat i(a_2(b_3+c_3)-a_3(b_2+c_2))-\hat j(a_1(b_3+c_3)-a_3(b_1+c_1))+\hat k (a_1(b_2+c_2)-a_2(a_1(b_2+c_3)))$
Now, $\vec a \times \vec b + \vec a \times \vec c=\begin{vmatrix} \hat i &\hat j & \hat k\\ a_1&a_2 &a_3 \\ b_1&b_2 &b_3 \end{vmatrix}+\begin{vmatrix} \hat i &\hat j & \hat k\\ a_1&a_2 &a_3 \\ c_1&c_2 &c_3 \end{vmatrix}$
$\vec a \times \vec b + \vec a \times \vec c=\hat i(a_2b_3-a_3b_2)-\hat j (a_1b_3-a_3b_1)+\hat k(a_1b_2-b_1a_2)+\hat i(a_2c_3-a_3c_2)-\hat j (a_1c_3-a_3c_1)+\hat k(a_1c_2-c_1a_2)$
$=\hat i(a_2(b_3+c_3)-a_3(b_2+c_2))-\hat j(a_1(b_3+c_3)-a_3(b_1+c_1))+\hat k (a_1(b_2+c_2)-a_2(a_1(b_2+c_3)))$
Hence, they are equal.
Question:8 If either $\vec a = \vec 0 \: \: or \: \: \vec b = \vec 0$ then $\vec a \times \vec b = \vec 0$ . Is the converse true? Justify your answer with an example.
Answer:
No, the converse of the statement is not true, as there can be two non-zero vectors, the cross product of whose is zero; they are collinear vectors.
Consider an example
$\vec a=\hat i +\hat j + \hat k$
$\vec b =2\hat i +2\hat j + 2\hat k$
Here $|\vec a| =\sqrt{1^2+1^2+1^2}=\sqrt{3}$
$|\vec b| =\sqrt{2^2+2^2+2^2}=2\sqrt{3}$
$\vec a \times \vec b=\begin{vmatrix} \hat i &\hat j &\hat k \\ 1&1 &1 \\ 2&2 &2 \end{vmatrix}=\hat i(2-2)-\hat j(2-2)+\hat k(2-2)=0$
Hence, the converse of the given statement is not true.
Question:9 Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).
Answer:
Given in the question
Vertices A = (1, 1, 2), B = (2, 3, 5) and C = (1, 5, 5). We need to find the area of the triangle
$AB=(2-1)\hat i+(3-1)\hat j+(5-2)\hat k=\hat i+2\hat j+3\hat k$
$BC=(1-2)\hat i+(5-3)\hat j+(5-5)\hat k=-\hat i+2\hat j$
Now, as we know
Area of the triangle,
$A=\frac{1}{2}|\vec {AB}\times\vec {BC}|=\frac{1}{2}|(\hat i+2\hat j +3\hat k)\times(-\hat i+2\hat j)|$
$=\frac{1}{2}\begin{vmatrix} \hat i &\hat j &\hat k \\ 1 &2 &3 \\ -1 &2 &0 \end{vmatrix}=\frac{1}{2}|\hat i(0-6)-\hat j(0-(-3))+\hat k(2-(-2))|$
$=\frac{1}{2}|-6\hat i-3\hat j+4\hat k|$
$=\frac{1}{2}×\sqrt{(-6)^2+(-3)^2+(4)^2}=\frac{\sqrt{61}}{2}$
So, the area of the triangle is $\frac{\sqrt{61}}{2}$ square units.
Question: 10 Find the area of the parallelogram whose adjacent sides are determined by the vectors $\vec a = \hat i - \hat j + 3 \hat k$ and $\vec b = 2\hat i -7 \hat j + \hat k$.
Answer:
Given in the question
$\vec a = \hat i - \hat j + 3 \hat k$
$\vec b = 2\hat i -7 \hat j + \hat k$
Area of parallelogram with adjescent side $\vec a$ and $\vec b$ ,
$A=|\vec a\times\vec b|=|(\vec i-\vec j+3\vec k)\times (2\hat i-7\hat j+\hat k)|$
$=\begin{vmatrix} \hat i& \hat j & \hat k\\ 1&-1 &3 \\ 2&-7 &1 \end{vmatrix}=|\hat i(-1+21)-\hat j (1-6)+\hat k (-7+2)|$
$=|\hat i(20)-\hat j (-5)+\hat k (-5)|=\sqrt{20^2+5^2+(-5)^2}$
$=\sqrt{450}=15\sqrt{2}$
So, the area of the parallelogram whose adjacent sides are determined by the vectors $\vec a = \hat i - \hat j + 3 \hat k$ and $\vec b = 2\hat i -7 \hat j + \hat k$ is $A=\sqrt{450}=15\sqrt{2}$ square units.
Question: 11 Let the vectors $\vec a \: \: and\: \: \vec b$ be such that $|\vec a| = 3 \: \: and\: \: |\vec b | = \frac{\sqrt 2 }{3}$ , then $\vec a \times \vec b$ is a unit vector, if the angle between $\vec a \: \:and \: \: \vec b$ is
$\\A ) \pi /6 \ B ) \pi / 4 \ C ) \pi / 3 \ D ) \pi /2$
Answer:
Given in the question,
$|\vec a| = 3 \: \: and\: \: |\vec b | = \frac{\sqrt 2 }{3}$
As given $\vec a \times \vec b$ is a unit vector, which means,
$|\vec a \times \vec b|=1$
⇒ $|\vec a| | \vec b|sin\theta=1$
⇒ $3×\frac{\sqrt{2}}{3}sin\theta=1$
⇒ $sin\theta=\frac{1}{\sqrt{2}}$
⇒ $\theta=\frac{\pi}{4}$
Hence, the angle between two vectors is $\frac{\pi}{4}$. The correct option is B.
Question: 12 Area of a rectangle having vertices A, B, C and D with position vectors
$- \hat i + \frac{1}{2} \hat j + 4 \hat k , \hat i + \frac{1}{2} \hat j + 4 \hat k , \hat i - \frac{1}{2}\hat j + 4 \hat k \: \: and \: \: - \hat i - \frac{1}{2} \hat j + 4 \hat k$
(A) $\frac{1}{2}$
(B) 1
(C) 2
(D) 4
Answer:
Given the four vertices of a rectangle are,
$\\\vec a=- \hat i + \frac{1}{2} \hat j + 4 \hat k , \\\vec b=\hat i + \frac{1}{2} \hat j + 4 \hat k , \\\vec c= \hat i - \frac{1}{2}\hat j + 4 \hat k \: \: and \: \: \\\vec d= - \hat i - \frac{1}{2} \hat j + 4 \hat k$
$\vec {AB}=\vec b-\vec a=(1+1)\hat i+(\frac{1}{2}-\frac{1}{2})\hat j+(4-4)\hat k=2\hat i$
$\vec {BC}=\vec c-\vec b=(1-1)\hat i+(-\frac{1}{2}-\frac{1}{2})\hat j+(4-4)\hat k=-\hat j$
Now, the Area of the Rectangle
$A=|\vec {AB}\times\vec {BC}|=|2\hat i \times (-\hat j)|=2$
Hence, option C is correct.
Vector Algebra Class 12 Chapter 10 - Miscellaneous Exercise
Page number: 372-373
Total questions: 19 |
Question: 1 Write down a unit vector in the XY-plane, making an angle of $30^\circ$ with the positive direction of the x-axis.
Answer:
As we know
A unit vector in XY-Plane making an angle $\theta$ with x-axis:
$\vec r=cos\theta \hat i+sin\theta \hat j$
Hence for $\theta = 30^0$
$\vec r=cos(30^0) \hat i+sin(30^0) \hat j$
$\vec r=\frac{\sqrt{3}}{2} \hat i+\frac{1}{2} \hat j$
Answer - the unit vector in XY-plane, making an angle of $30 ^\circ$ with the positive direction of x-axis is
$\vec r=\frac{\sqrt{3}}{2} \hat i+\frac{1}{2} \hat j$
Question: 2 Find the scalar components and magnitude of the vector joining the points
$P(x_1, y_1, z_1) \: \: and \: \: Q(x_2, y_2, z_2).$
Answer:
Given in the question
$P(x_1, y_1, z_1) \: \: and \: \: Q(x_2, y_2, z_2).$
And we need to finrd the scalar components and magnitude of the vector joining the points P and Q
$\vec {PQ}=(x_2-x_1)\hat i +(y_2-y_1)\hat j+(z_2-z_1)\hat k$
Magnitiude of vector PQ
$|\vec {PQ}|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2}$
Scalar components are
$(x_2-x_1),(y_2-y_1),(z_2-z_1)$
Question: 3 A girl walks 4 km towards west, then she walks 3 km in a direction $30^\circ$ east of north and stops. Determine the girl’s displacement from her initial point of departure.
Answer:
As the girl walks 4km towards west
Position vector = $-4\hat i$
Now, as she moves 3km in the direction 30 degree east of north.
$-4\hat i+3sin30^0\hat i+3cos30^0\hat j$
$-4\hat i+\frac{3}{2}\hat i+3\frac{\sqrt{3}}{2}\hat j$
$\frac{-5}{2}\hat i+3\frac{\sqrt{3}}{2}\hat j$
Hence, final position vector is;
$\frac{-5}{2}\hat i+3\frac{\sqrt{3}}{2}\hat j$.
Question: 4 If $\vec a = \vec b + \vec c$ , then is it true that $|\vec a| =| \vec b |+| \vec c |$ ? Justify your answer.
Answer:
No, if $\vec a = \vec b + \vec c$ then we can not conclude that $|\vec a| =| \vec b |+| \vec c |$ .
the condition $\vec a = \vec b + \vec c$ satisfies in the triangle.
also, in a triangle, $|\vec a| <| \vec b |+| \vec c |$
Since, the condition $|\vec a| =| \vec b |+| \vec c |$ is contradicting with the triangle inequality, if $\vec a = \vec b + \vec c$ then we can not conclude that $|\vec a| =| \vec b |+| \vec c |$
Question: 5 Find the value of x for which $x ( \hat i+ \hat j + \hat k )$ is a unit vector.
Answer:
Given in the question,
a unit vector, $\vec u=x ( \hat i+ \hat j + \hat k )$
We need to find the value of x
$|\vec u|=1$
$|x ( \hat i+ \hat j + \hat k )|=1$
$x\sqrt{1^2+1^2+1^2}=1$
$x\sqrt{3}=1$
$x=\frac{1}{\sqrt{3}}$
The value of x is $\frac{1}{\sqrt{3}}$
Question: 6 Find a vector of magnitude 5 units, and parallel to the resultant of the vectors $\vec a = 2 \hat i + 3 \hat j - \hat k \: \: and \: \: \vec b = \hat i - 2 \hat j + \hat k$
Answer:
Given two vectors
$\vec a = 2 \hat i + 3 \hat j - \hat k \: \: and \: \: \vec b = \hat i - 2 \hat j + \hat k$
Resultant of $\vec a$ and $\vec b$ :
$\vec R = \vec a +\vec b$ $=2 \hat i + 3 \hat j - \hat k + \hat i - 2 \hat j + \hat k=3\hat i + \hat j$
Now, a unit vector in the direction of $\vec R$
$\vec u =\frac{3\hat i+\hat j}{\sqrt{3^2+1^2}}=\frac{3}{\sqrt{10}}\hat i+\frac{1}{\sqrt{10}}\hat j$
Now, a unit vector of magnitude in the direction of $\vec R$
$\vec v=5\vec u =5*\frac{3}{\sqrt{10}}\hat i+5*\frac{1}{\sqrt{10}}\hat j=\frac{15}{\sqrt{10}}\hat i+\frac{5}{\sqrt{10}}\hat j$
Hence, the required vector is $\frac{15}{\sqrt{10}}\hat i+\frac{5}{\sqrt{10}}\hat j$
Question:7 If $\vec a = \hat i + \hat j + \hat k , \vec b = 2 \hat i - \hat j + 3 \hat k \: \: and\: \: \vec c = \hat i - 2 \hat j + \hat k$ , find a unit vector parallel to the vector $2\vec a - \vec b + 3 \vec c$ .
Answer:
Given in the question,
$\vec a = \hat i + \hat j + \hat k , \vec b = 2 \hat i - \hat j + 3 \hat k \: \: and\: \: \vec c = \hat i - 2 \hat j + \hat k$
Now,
let vector $\vec V=2\vec a - \vec b + 3 \vec c$
$\vec V=2(\hat i +\hat j +\hat k) - (2\hat i-\hat j+3\hat k)+ 3 (\hat i-2\hat j+\hat k)$
$\vec V=3\hat i-3\hat j+2\hat k$
Now, a unit vector in direction of $\vec V$
$\vec u =\frac{3\hat i-3\hat j+2\hat k}{\sqrt{3^2+(-3)^2+2^2}}=\frac{3}{\sqrt{22}}\hat i-\frac{3}{\sqrt{22}} \hat j+\frac{2}{\sqrt{22}}\hat k$
Now,
A unit vector parallel to $\vec V$
$\vec u =\frac{3}{\sqrt{22}}\hat i-\frac{3}{\sqrt{22}} \hat j+\frac{2}{\sqrt{22}}\hat k$
OR
$-\vec u =-\frac{3}{\sqrt{22}}\hat i+\frac{3}{\sqrt{22}} \hat j-\frac{2}{\sqrt{22}}\hat k$
Question: 8 Show that the points A(1, – 2, – 8), B(5, 0, –2), and C(11, 3, 7) are collinear, and find the ratio in which B divides AC.
Answer:
Given in the question,
points A(1, – 2, – 8), B(5, 0, –2) and C(11, 3, 7)
$\vec {AB }=(5-1)\hat i+(0-(-2))\hat j+(-2-(-8))\hat k=4\hat i+2\hat j+6\hat k$
$\vec {BC }=(11-5)\hat i+(3-0)\hat j+(7-(-2))\hat k=6\hat i+3\hat j+9\hat k$
$\vec {CA }=(11-1)\hat i+(3-(-2))\hat j+(7-(-8))\hat k=10\hat i+5\hat j+15\hat k$
Now let's calculate the magnitude of the vectors
$|\vec {AB }|=\sqrt{4^2+2^2+6^2}=\sqrt{56}=2\sqrt{14}$
$|\vec {BC }|=\sqrt{6^2+3^2+9^2}=\sqrt{126}=3\sqrt{14}$
$|\vec {CA }|=\sqrt{10^2+5^2+15^2}=\sqrt{350}=5\sqrt{14}$
As we see that AB = BC + AC, we conclude that the three points are collinear.
We can also see from here,
Point B divides AC in the ratio 2 : 3.
Question:9 Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are $( 2 \vec a + \vec b ) \: \: and \: \: ( \vec a - 3 \vec b )$ externally in the ratio 1: 2. Also, show that P is the mid point of the line segment RQ.
Answer:
Given, two vectors $\vec P=( 2 \vec a + \vec b ) \: \:and \: \:\vec Q= ( \vec a - 3 \vec b )$
The point R, which divides line segment PQ in ratio 1:2 is given by
$=\frac{2(2\vec a +\vec b)-(\vec a-3\vec b)}{2-1}=4\vec a +2\vec b -\vec a+3\vec b=3\vec a+5\vec b$
Hence, the position vector of R is $3\vec a+5\vec b$ .
Now, the Position vector of the midpoint of RQ
$=\frac{( 3\vec a + 5\vec b + \vec a - 3 \vec b )}{2}=2\vec a+\vec b$
which is the position vector of Point P . Hence, P is the mid-point of RQ
Question:10 The two adjacent sides of a parallelogram are $2 \hat i - 4 \hat j + 5 \hat k \: \:and \: \: \hat i - 2 \hat j - 3 \hat k$ . Find the unit vector parallel to its diagonal. Also, find its area.
Answer:
Given two adjacent sides of the parallelogram
$2 \hat i - 4 \hat j + 5 \hat k \: \:and \: \: \hat i - 2 \hat j - 3 \hat k$
The diagonal will be the resultant of these two vectors. so
resultant R:
$\vec R=2 \hat i - 4 \hat j + 5 \hat k \: +\: \hat i - 2 \hat j - 3 \hat k=3\hat i-6\hat j+2\hat k$
Now the unit vector in the direction of R
$\vec u=\frac{3\hat i-6\hat j+2\hat k}{\sqrt{3^2+(-6)^2+2^2}}=\frac{3\hat i-6\hat j+2\hat k}{\sqrt{49}}=\frac{3\hat i-6\hat j+2\hat k}{7}$
Hence unit vector along the diagonal of the parallelogram
$\vec u={\frac{3}{7}\hat i-\frac{6}{7}\hat j+\frac{2}{7}\hat k}$
Now,
Area of parallelogram
$A=(2 \hat i - 4 \hat j + 5 \hat k )\: \times \: \: (\hat i - 2 \hat j - 3 \hat k)$
$A=\begin{vmatrix} \hat i &\hat j &\hat k \\ 2& -4 &5 \\ 1&-2 &-3 \end{vmatrix}=|\hat i(12+10)-\hat j(-6-5)+\hat k(-4+4)|=|22\hat i +11\hat j|$
$A=\sqrt{22^2+11^2}=11\sqrt{5}$
Hence, the area of the parallelogram is $11\sqrt{5}$.
Question: 11 Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are $\pm \left ( \frac{1}{\sqrt 3 } , \frac{1}{\sqrt 3 } , \frac{1}{\sqrt 3 } \right )$
Answer:
Let a vector $\vec a$ is equally inclined to axis OX, OY and OZ.
let direction cosines of this vector be
$cos\alpha,cos\alpha \:and \:cos\alpha$
Now
$cos^2\alpha+cos^2\alpha +cos^2\alpha=1$
$cos^2\alpha=\frac{1}{3}$
$cos\alpha=\frac{1}{\sqrt{3}}$
Hence, direction cosines are:
$\left ( \frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} \right )$.
Question: 12 Let $\vec a = \hat i + 4 \hat j + 2 \hat k , \vec b = 3 \hat i - 2 \hat j + 7 \hat k \: \:and \: \: \vec c = 2 \hat i - \hat j + 4 \hat k$ . Find a vector $\vec d$ which is perpendicular to both $\vec a \: \: and \: \: \vec b \: \: and \: \: \vec c . \vec d = 15$
Answer:
Given,
$\vec a = \hat i + 4 \hat j + 2 \hat k , \vec b = 3 \hat i - 2 \hat j + 7 \hat k \: \:and \: \: \vec c = 2 \hat i - \hat j + 4 \hat k$
Let $\vec d=d_1\hat i+d_2\hat j +d_3\hat k$
now, since it is given that d is perpendicular to $\vec a$ and $\vec b$ , we got the condition,
$\vec b.\vec d=0$ and $\vec a.\vec d=0$
$(\hat i+4\hat j +2\hat k)\cdot(d_1\hat i +d_2\hat j+d_3\hat k)=0$ And $(3\hat i-2\hat j +7\hat k)\cdot(d_1\hat i +d_2\hat j+d_3\hat k)=0$
$d_1+4d_2+2d_3=0$ And $3d_1-2d_2+7d_3=0$
here we got 2 equation and 3 variable. one more equation will come from the condition:
$\vec c . \vec d = 15$
$(2\hat i-\hat j +4\hat k)\cdot(d_1\hat i +d_2\hat j+d_3\hat k)=15$
$2d_1-d_2+4d_3=15$
so now we have three equation and three variable,
$d_1+4d_2+2d_3=0$
$3d_1-2d_2+7d_3=0$
$2d_1-d_2+4d_3=15$
On solving this three equation we get,
$d_1=\frac{160}{3},d_2=-\frac{5}{3}\:and\:d_3=-\frac{70}{3}$ ,
Hence, Required vector :
$\vec d=\frac{160}{3}\hat i-\frac{5}{3}\hat j-\frac{70}{3}\hat k$.
Question: 13 The scalar product of the vector $\hat i + \hat j + \hat k$ with a unit vector along the sum of vectors $2\hat i + 4 \hat j -5 \hat k$ and $\lambda \hat i + 2 \hat j +3 \hat k$ is equal to one. Find the value of $\lambda$ .
Answer:
Let, the sum of vectors $2\hat i + 4 \hat j -5 \hat k$ and $\lambda \hat i + 2 \hat j +3 \hat k$ be
$\vec a=(\lambda +2)\hat i + 6 \hat j -2 \hat k$
unit vector along $\vec a$
$\vec u=\frac{(\lambda +2)\hat i + 6 \hat j -2 \hat k}{\sqrt{(\lambda+2)^2+6^2+(-2)^2}}=\frac{(\lambda +2)\hat i + 6 \hat j -2 \hat k}{\sqrt{\lambda^2+4\lambda+44}}$
Now, the scalar product of this with $\hat i + \hat j + \hat k$
$\vec u.(\hat i+\hat j +\hat k)=\frac{(\lambda +2)\hat i + 6 \hat j -2 \hat k}{\sqrt{\lambda^2+4\lambda+44}}.(\hat i+\hat j +\hat k)$
$\vec u.(\hat i+\hat j +\hat k)=\frac{(\lambda +2) + 6 -2 }{\sqrt{\lambda^2+4\lambda+44}}=1$
$\frac{(\lambda +2) + 6 -2 }{\sqrt{\lambda^2+4\lambda+44}}=1$
$\frac{(\lambda +6) }{\sqrt{\lambda^2+4\lambda+44}}=1$
$\lambda =1$
Question: 14 If $\vec a , \vec b , \vec c$ are mutually perpendicular vectors of equal magnitudes, show that the vector $\vec a+\vec b +\vec c$ is equally inclined to $\vec a , \vec b \: \: and \: \: \vec c$ .
Answer:
Given
$|\vec a|=|\vec b|=|\vec c|$ and
$\vec a.\vec b=\vec b.\vec c=\vec c.\vec a=0$
Now, let vector $\vec a+\vec b +\vec c$ is inclined to $\vec a , \vec b \: \: and \: \: \vec c$ at $\theta_1,\theta_2\:and\:\theta_3$ respectively.
Now,
$cos\theta_1=\frac{(\vec a+\vec b+\vec c).\vec a}{|\vec a+\vec b+\vec c||\vec a|}=\frac{\vec a.\vec a +\vec a.\vec b +\vec c.\vec a}{|\vec a+\vec b+\vec c||\vec a|}=\frac{\vec a.\vec a}{|\vec a+\vec b+\vec c||\vec a|}=\frac{|\vec a|}{|\vec a+\vec b+\vec c|}$
$cos\theta_2=\frac{(\vec a+\vec b+\vec c).\vec b}{|\vec a+\vec b+\vec c||\vec b|}=\frac{\vec a.\vec b +\vec b.\vec b +\vec c.\vec b}{|\vec a+\vec b+\vec c||\vec b|}=\frac{\vec b.\vec b}{|\vec a+\vec b+\vec c||\vec b|}=\frac{|\vec b|}{|\vec a+\vec b+\vec c|}$
$cos\theta_3=\frac{(\vec a+\vec b+\vec c).\vec c}{|\vec a+\vec b+\vec c||\vec c|}=\frac{\vec a.\vec c +\vec b.\vec c +\vec c.\vec c}{|\vec a+\vec b+\vec c||\vec c|}=\frac{\vec c.\vec c}{|\vec a+\vec b+\vec c||\vec c|}=\frac{|\vec c|}{|\vec a+\vec b+\vec c|}$
Now, Since, $|\vec a|=|\vec b|=|\vec c|$
$cos\theta_1=cos\theta_2=cos\theta_3$
$\theta_1=\theta_2=\theta_3$
Hence vector $\vec a+\vec b +\vec c$ is equally inclined to $\vec a , \vec b \: \: and \: \: \vec c$.
Question: 15 Prove that $( \vec a + \vec b ) . (\vec a + \vec b ) = |\vec a ^2 | + |\vec b |^2$ , if and only if $\vec a , \vec b$ are perpendicular, given $\vec a \neq 0 , \vec b \neq 0$
Answer:
Given in the question,
are perpendicular and we need to prove that 
LHS= 
if 
are perpendicular, 
= RHS
LHS is equal to RHS.
Hence proved.
Question: 16 Choose the correct answer If $\theta$ is the angle between two vectors $\vec a \: \: and \: \: \vec b$ , then $\vec a \cdot \vec b \geq 0$ only when
$\\A ) 0 < \theta < \frac{\pi }{2} \\\\ \: \: \: \: B ) 0 \leq \theta \leq \frac{\pi }{2} \\\\ \: \: \: C ) 0 < \theta < \pi \\\\ \: \: \: D) 0 \leq \theta \leq\pi$
Answer:
Given in the question
$\theta$ is the angle between two vectors $\vec a \: \: and \: \: \vec b$
$\vec a \cdot \vec b \geq 0$
$|\vec a| | \vec b |cos\theta\geq 0$
this will satisfy when
$cos\theta\geq 0$
$0\leq\theta\leq \frac{\pi}{2}$
Hence, option B is the correct answer.
Question 17 Choose the correct answer. Let $\vec a \: \: and \: \: \vec b$ be two unit vectors and $\theta$ is the angle between them. Then $\vec a + \vec b$ is a unit vector if
$\\A ) \theta = \frac{\pi }{4} \\\\ B ) \theta = \frac{\pi }{3} \\\\ C ) \theta = \frac{\pi }{2} \\\\ D ) \theta = \frac{2\pi }{3}$
Answer:
Given in the question
$\vec a \: \: and \: \: \vec b$ be two unit vectors and $\theta$ is the angle between them
$|\vec a|=1,\:and\:\:|\vec b|=1$
also
$|\vec a + \vec b|=1$
$|\vec a + \vec b|^2=1$
$|\vec a|^2 + |\vec b|^2+2\vec a.\vec b=1$
$1 + 1+2\vec a.\vec b=1$
$\vec a.\vec b=-\frac{1}{2}$
$|\vec a||\vec b|cos\theta =-\frac{1}{2}$
$cos\theta =-\frac{1}{2}$
$\theta =\frac{2\pi}{3}$
Then $\vec a + \vec b$ is a unit vector if $\theta =\frac{2\pi}{3}$
Hence, option D is correct.
Question:18 The value of $\hat i ( \hat j \times \hat k ) + \hat j ( \hat i \times \hat k ) + \hat k ( \hat i \times \hat j )$ is
(A) 0
(B) –1
(C) 1
(D) 3
Answer:
To find the value of $\hat i ( \hat j \times \hat k ) + \hat j ( \hat i \times \hat k ) + \hat k ( \hat i \times \hat j )$
$\\\hat i ( \hat j \times \hat k ) + \hat j ( \hat i \times \hat k ) + \hat k ( \hat i \times \hat j ) \\=\hat i.\hat i+\hat j(-\hat j)+\hat k.\hat k\\=1-1+1\\=1$
Hence, option C is correct.
Question: 19 Choose the correct. If $\theta$ is the angle between any two vectors $\vec a \: \:and \: \: \vec b$ , then $|\vec a \cdot \vec b |=|\vec a \times \vec b |$ when $\theta$
is equal to
$\\A ) 0 \\\\ B ) \pi /4 \\\\ C ) \pi / 2 \\\\ D ) \pi$
Answer:
Given in the question
$\theta$ is the angle between any two vectors $\vec a \: \:and \: \: \vec b$ and $|\vec a \cdot \vec b |=|\vec a \times \vec b |$
To find the value of $\theta$
Hence, option D is correct.
