NCERT Exemplar Class 12th Maths Solutions Chapter 11 Three Dimensional Geometry 2021

NCERT Exemplar Class 12th Maths Solutions Chapter 11 Three Dimensional Geometry

Edited By Ravindra Pindel | Updated on Sep 15, 2022 05:16 PM IST | #CBSE Class 12th

Upcoming Event

CBSE Class 12th Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT exemplar Class 12 Maths solutions chapter 11 Three Dimensional Geometry - If you observe the world around you, you see everything in three dimensions! Even a tiny strand of hair has dimensions of length, width, and depth. 3D geometry refers to the mathematics of perception, direction, and shape. NCERT exemplar Class 12 Maths chapter 11 solutions initiates that there is always a requirement of three parameters to work with the comprehensive concepts of three-dimensional geometry. NCERT exemplar solutions For Class 12 Maths chapter 11 would help you out in any three-dimensional Mathematical problem that you're stuck on and get you back in your study loop. NCERT exemplar Class 12 Maths solutions chapter 11 PDF download is helpful for students to learn offline when there is a slow internet connection. Also, read - NCERT Class 12 Maths Solutions

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

This Story also Contains

Main Subtopics of NCERT Exemplar Class 12 Maths Solutions Chapter 11
What will the students learn in NCERT Exemplar Class 12 Maths Solutions Chapter 11?
NCERT Exemplar Class 12 Maths Solutions
Importance of NCERT Exemplar Class 12 Maths Solutions Chapter 11

Question:1

Find the position vector of a point A in space, so that $\overline{OA}$ is inclined at 60? to $\overline{OX}$ and 45? to $\overline{OY}$ and $\left |\overline{OA} \right |$ = 10 units.

Answer:

Given, $\overline{OA}$ is inclined at 60⁰ to and at $\overline{OX}$ 45⁰ to $\overline{OY}$
$\overline{OA}$ = 10 units.
We want to find the position vector of point A in space, which is nothing but $\overline{OA}$
We know, there are three axes in space: X, Y, and Z.
Let OA be inclined with OZ at an angle α.
We know, directions cosines are associated by the relation:
l² + m² + n² = 1 ….(i)
In this question, direction cosines are the cosines of the angles inclined by on $\overline{OA}$ , $\overline{OX}$ , $\overline{OY}$ and $\overline{OZ}$
So, $l=\cos 60^{\circ},m=\cos 45^{\circ},n=\cos \alpha$
Substituting the values of l, m, and n in equation (i),
$\left (\cos 60^{\circ} \right )^{2}+\left (m=\cos 45^{\circ} \right )^{2}+\left (n=\cos \alpha \right )^{2}=1$
We know the values of $\cos 60^{\circ}$ and $\cos 45^{\circ}$ , i.e. 1/2 and 1/√2 respectively.
Therefore, we get
$\left ( \frac{1}{2} \right )^{2}+\left ( \frac{1}{\sqrt{2}} \right )^{2}+\cos^{2}\alpha =1$
$\Rightarrow \frac{1}{4}+\frac{1}{2}+\cos^{2}\alpha =1$
$\Rightarrow \cos^{2}\alpha =1-\frac{1}{4}-\frac{1}{2}$
$\Rightarrow \cos^{2}\alpha =\frac{4-1-2}{4}$
$\Rightarrow \cos^{2}\alpha =\frac{1}{4}$
$\Rightarrow \cos \alpha =\pm \sqrt{\frac{1}{4}}$
$\Rightarrow \cos \alpha =\pm \frac{1}{2}$
So $\overrightarrow{OA}$ is given as
$\overrightarrow{OA}=\overrightarrow{OA}\left ( l\hat{i}+m\hat{j}+n\hat{k} \right )$ ..........(ii)
We have,
$l = \cos 60^{\circ} = \frac{1}{2}\\ m =\ cos 45^{\circ} = \frac{1}{\sqrt{2}}\\ n = \cos \alpha = \pm \frac{1}{2}\\$
Inserting these values of l, m and n in equation (ii),
$\overrightarrow{OA}=\left |\overrightarrow{OA} \right |\left ( \frac{1}{2} \hat{i}+\frac{1}{\sqrt{2}}\hat{j}+\frac{1}{2}\hat{k} \right )$
Also ,Put 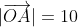$|\overrightarrow{OA}| =10$ $\Rightarrow \overrightarrow{OA}=10\left ( \frac{1}{2} \hat{i}+\frac{1}{\sqrt{2}}\hat{j}+\frac{1}{2}\hat{k} \right )$
$\Rightarrow \overrightarrow{OA}=10\times \frac{1}{2} \hat{i}+10\times\frac{1}{\sqrt{2}}\hat{j}+10\times\frac{1}{2}\hat{k}$
$\Rightarrow \overrightarrow{OA}=5i+10\times\frac{\sqrt{2}}{\sqrt{2}}\times+10\times\frac{1}{\sqrt{2}}\hat{j}\pm 5\hat{k}$
$\Rightarrow \overrightarrow{OA}=5i+\frac{10\times\sqrt{2}}{2}\hat{j}\pm 5\hat{k}$
$\Rightarrow \overrightarrow{OA}=5i+5\sqrt{2}\hat{j}\pm 5\hat{k}$
Thus, position vector of A in space $=5i+5\sqrt{2}\hat{j}\pm 5\hat{k}$

Question:2

Find the vector equation of the line parallel to the vector $3\hat{i}-2 \hat{j}+3\hat{k}$ and which passes through the point (1, -2, 3).

Answer:

Given, vector = $3\hat{i}-2\hat{j}+6\hat{k}$

Point = (1, -2, 3)

We can write this point in vector form as $\hat{i}-2\hat{j}+3\hat{k}$

Let ,

$\overrightarrow{a}=\hat{i}-2\hat{j}+3\hat{k}$

$\overrightarrow{b}=3\hat{i}-2\hat{j}+6\hat{k}$

We must find the vector equation of the line parallel to the vector $\overrightarrow{b}$ and passing through the point

We know, equation of $\overrightarrow{r}=\overrightarrow{a}+\lambda \overrightarrow{b}$ a line passing through a point and parallel to a given vector is denoted as

Where, $\lambda \epsilon \mathbb{R}$

In other words, we need to find $\overrightarrow{r}$

This can be achieved by substituting the values of the vectors in the above equation. We get

$\overrightarrow{r}=\left ( \hat{i}-2\hat{j}+3\hat{k} \right )+\lambda \left ( 3\hat{i}-2\hat{j}+6\hat{k} \right )$

$\Rightarrow \overrightarrow{r}=\left ( \hat{i}-2\hat{j}+3\hat{k} \right )+\lambda \left ( 3\hat{i}-2\hat{j}+6\hat{k} \right )$

This can be further rearranged, upon which we get:

$\Rightarrow \vec{r}=\hat{i}-2\hat{j}+3\hat{k}+3\lambda \hat{j}+3\hat{k}+6\lambda\hat{k}$

$\Rightarrow \vec{r}=\hat{i}+3\lambda \hat{i}-2\hat{j}-2\lambda\hat{j}+3\hat{k}+6\lambda\hat{k}$

$\Rightarrow \vec{r}=\left ( 1-3\lambda \right )\hat{i}+\left ( -2-2\lambda \right )\hat{j}+\left ( 3+6\lambda \right )\hat{k}$

Thus, the require vector equation of line is $\vec{r}=\left ( \hat{i}-2\hat{j}+3\hat{k} \right )+\lambda\left ( 3\hat{i}-2\hat{j}+6\hat{k} \right )$

which can also be written as $\left ( 1-3\lambda \right )i+\left ( -2-2 \lambda \right )\hat{j}+\left ( 3+6\lambda \right )\hat{k}$

Question:3

Show that the given lines, $\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}$ and $\frac{x-4}{5}=\frac{y-1}{2}=z$ intersect.
Also, find the point of intersection of the lines.

Answer:

We have the lines,
$\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}$
$\frac{x-4}{5}=\frac{y-1}{2}=z$
Let us denote these lines as L₁and L₂, such that
$L_{1}:\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda$
$L_{2}=\frac{x-4}{5}=\frac{y-1}{2}=z=\mu$
where $\lambda ,\mu \epsilon \mathbb{R}$
We must show that the lines L₁and L₂ intersect.
To show this, let us first find any point on line L₁ and line L₂
For L₁:
$L_{1}:\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda$
$\Rightarrow \frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\lambda$
$\Rightarrow \frac{x-1}{2}=\lambda,\frac{y-2}{3}=\lambda,\frac{z-3}{4}=\lambda$
We must find the values of x, y, and z. Therefore, let us take $\Rightarrow \frac{x-1}{2}=\lambda$
$\Rightarrow x-1=2\lambda$
$\Rightarrow x=2\lambda+1$
Take $\frac{y-2}{3}=\lambda$
$\Rightarrow y-2=3\lambda$
$\Rightarrow y=3 \lambda+2$
Take $\frac{z-3}{4}=\lambda$
$\Rightarrow z-3=4\lambda$
$\Rightarrow z=4\lambda+3...(i)$
Therefore, any point on L₁ can be represented as $(2\lambda + 1, 3\lambda + 2, 4\lambda + 3)$ .
Now,
For L₂:
$L_{2}=\frac{x-4}{5}=\frac{y-1}{2}=z=\mu$
$\Rightarrow \frac{x-4}{5}=\frac{y-1}{2}=z=\mu$
$\Rightarrow \frac{x-4}{5}=\mu,\frac{y-1}{2}=\mu,z=\mu$
We must find the values of x, y, and z. Therefore,
Take $\frac{x-4}{5}=\mu$
$\Rightarrow x-4=5\mu$
$\Rightarrow x=5\mu+4$
Take $\frac{y-1}{2}=\mu$
$\Rightarrow y-1=2\mu$
$\Rightarrow y=2\mu+1$
Take $z=\mu$
$\Rightarrow z=\mu........(ii)$
Hence, any point on line L? can be represented as (5μ + 4, 2μ + 1, μ).
If lines L₁ and L₂ intersect, then there exist λ and μ such that
$\left ( 2\lambda+1,3\lambda+3,4\lambda+3 \right )\equiv \left ( 5\mu+4,2\mu+1,\mu \right )$
$\Rightarrow 2\lambda+1= 5\mu+4......(iii)$
$3\lambda+2=2\mu+1.....(iv)$
$4\lambda+3=\mu.....(iv)$
Substituting the value of μ from equation (v) into equation (iv),
$3\lambda+2=2\left ( 4\lambda+3 \right )+1$
$\Rightarrow 3\lambda+2=8\lambda+6+1$
$\Rightarrow 3\lambda+2=8\lambda+7$
$\Rightarrow 8\lambda-3\lambda=2-7$
$\Rightarrow 5\lambda=-5$
$\Rightarrow \lambda=-\frac{5}{5}$
$\Rightarrow \lambda=-1$
Putting this value of $\lambda$ in eq (v),
$4\left ( -1 \right )+3=\mu$
$\Rightarrow \mu=-4+3$
$\Rightarrow \mu=-1$
To check, we can substitute the values of $\lambda$ and $\mu$ in equation (iii), giving us:
$2(-1) + 1 = 5(-1) + 4$
$\Rightarrow -2 + 1 = -5 + 4$
$\Rightarrow -1 = -1$
Therefore $\lambda$ and $\mu$ also satisfy equation (iii).
So, the z-coordinate from equation (i),
$z=4\lambda +3$
$\Rightarrow z=4\left ( -1 \right )+3 \left [ \because \lambda=-1 \right ]$
$\Rightarrow z=-4+3$
$\Rightarrow z=-1$
And the z-coordinate from equation (ii),
$z=\mu$
$z=-1\left [ \because \mu=-1 \right ]$
So, the lines intersect at the point
$(5\mu + 4, 2\mu + 1, \mu) = (5(-1) + 4, 2(-1) + 1, -1).\\ Or, (5\mu + 4, 2\mu + 1, \mu) = (-5 + 4, -2 + 1, -1)\\ Or (5\mu + 4, 2\mu + 1, \mu) = (-1, -1, -1)$
Therefore the lines intersect at the point (-1, -1, -1).

Question:4

Find the angle between the lines $\vec{r}=3\hat{i}-2\hat{j}+6\hat{k}+\lambda \left ( 2 \hat{i}+\hat {j}+2\hat{k} \right )$ and 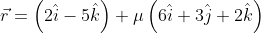$\vec{r}= \left(2 \hat{i}-5\hat{k} \right )+\mu \left ( 6\hat{i}+3\hat {j}+2\hat{k} \right )$

Answer:

Given, lines:
$\vec{r}=3\hat{i}-2\hat{j}+6\hat{k}+\lambda\left ( 2\hat{i}+\hat{j}+2\hat{k} \right )$
$\vec{r}=\left (2\hat{i}-5\hat{k} \right )+\mu\left ( 6\hat{i}+3\hat{j}+2\hat{k} \right )$
We are instructed to find the angle between the lines.
The line $\vec{r}=3\hat{i}-2\hat{j}+6\hat{k}+\lambda\left ( 2\hat{i}+\hat{j}+2\hat{k} \right )$ is parallel to the vector
$2\hat{i}+\hat{j}+2\hat{k}$
Let
$\vec{b_{1}}=2\hat{i}+\hat{j}+2\hat{k}$

Then, we can say the line $\vec{r}=3\hat{i}-2\hat{j}+6\hat{k}+\lambda\left ( 2\hat{i}+\hat{j}+2\hat{k} \right )$ is parallel to vector $\vec{b_{1}}=2\hat{i}+\hat{j}+2\hat{k}$
Similarly, let $\vec{b_{2}}=6\hat{i}+3\hat{j}+2\hat{k}$
Then, we can say is $\vec{r}=2\hat{j}-5\hat{k}+\mu \left ( 6\hat{i}+3\hat{j}+2\hat{k} \right )$ parallel to the vector $\vec{b_{2}}=6\hat{i}+3\hat{j}+2\hat{k}$
If we take θ as the angle between the lines, then cosine θ is:
$\cos \theta = \frac{\vec{b_{1}}\vec{b_{2}}}{\left |\vec{b_{1}} \right |\left |\vec{b_{2}} \right |}$
Substituting the values of $\vec{b_{1}}=2\hat{i}+\hat{j}+2\hat{k}$ and $\vec{b_{2}}=6\hat{i}+3\hat{j}+2\hat{k}$ in the above equation,
We get
$\cos \theta=\frac{\left ( 2\hat{i}+\hat{j}+2\hat{k} \right )\left ( 6\hat{i}+3\hat{j}+2\hat{k} \right )}{\left | 2\hat{i}+\hat{j}+2\hat{k} \right |\left | 6\hat{i}+3\hat{j}+2\hat{k} \right |}$
Here,
$\left ( 2\hat{i}+\hat{j}+2\hat{k} \right )\left ( 6\hat{i}+3\hat{j}+2\hat{k} \right )=\left ( 2 \times 6 \right )+\left ( 1 \times 3 \right )+\left ( 2 \times 2 \right )$
$\left ( 2\hat{i}+\hat{j}+2\hat{k} \right )\left ( 6\hat{i}+3\hat{j}+2\hat{k} \right )=12+3+4$
$\left ( 2\hat{i}+\hat{j}+2\hat{k} \right )\left ( 6\hat{i}+3\hat{j}+2\hat{k} \right )=19...........(i)$
Also,
$\left |2\hat{i}+\hat{j}+2\hat{k} \right |\left | 6\hat{i}+3\hat{j}+2\hat{k} \right |=\sqrt{2^{2}+1^{2}+2^{2}}\sqrt{6^{2}+3^{2}+2^{2}}$
$\left |2\hat{i}+\hat{j}+2\hat{k} \right |\left | 6\hat{i}+3\hat{j}+2\hat{k} \right |=\sqrt{4+1+4}\sqrt{36+9+4}$
$\left |2\hat{i}+\hat{j}+2\hat{k} \right |\left | 6\hat{i}+3\hat{j}+2\hat{k} \right |=\sqrt{9}\sqrt{49}$
$\left |2\hat{i}+\hat{j}+2\hat{k} \right |\left | 6\hat{i}+3\hat{j}+2\hat{k} \right |=3 \times 7$
$\left |2\hat{i}+\hat{j}+2\hat{k} \right |\left | 6\hat{i}+3\hat{j}+2\hat{k} \right |=21............(ii)$
Substituting the values of $\cos \theta$ in equation (i) and (ii), we get
$\cos \theta=\frac{19}{21}$
$\Rightarrow \theta=\cos^{-1}\left (\frac{19}{21} \right )$
Therefore, the angle between the lines is $\cos^{-1}\left (\frac{19}{21} \right )$

Question:5

Prove that the line through points A (0, -1, -1) and B (4, 5, 1) intersects the line through C (3, 9, 4 ) and D (-4, 4, 4).

Answer:

Given: A (0, -1, -1), B (4, 5, 1), C (3, 9, 4), D (-4, 4, 4).
To prove: The line passing through A and B intersects the line passing through C and D.
Proof: We know, equation of a line passing through two points (x₁ , y₁ , z₁) and (x₂ , y₂ , z₂) is:
$\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}$
Hence, the equation of the line passing through A (0, -1, -1) and B (4, 5,1) is:
$\frac{x-0}{4-0}=\frac{y-(-1)}{5-(-1)}=\frac{z-(-1)}{1-(-1)}$
, where x₁ = 0, y₁ = -1, z₁ = -1; and x₂ = 4, y₂ = 5, z₂ = 1
$\Rightarrow \frac{x-0}{4}=\frac{y+1}{6}=\frac{z+1}{2}\\ \Rightarrow \frac{x}{4}=\frac{y+1}{6}=\frac{z+1}{2}$
Let
$L_{1}: \frac{x}{4}=\frac{y+1}{6}=\frac{z+1}{2}=\lambda\\ \\ \frac{x}{4}=\lambda, \frac{y+1}{6}=\lambda,\frac{z+1}{2}=\lambda\\$
We must find the values of x, y, and z. Therefore,
$Take \frac{x}{4}=\lambda\\ \Rightarrow x=4\lambda\\ \\ Take \frac{y+1}{6}=\lambda\\ \Rightarrow y+1=6\lambda\\ \Rightarrow y=6\lambda-1\\ \\ Take \frac{z+1}{2}=\lambda\\ \Rightarrow z+1=2\lambda\\ \Rightarrow z=2\lambda-1\\ \\$
This implies that any point on the line L₁ is (4λ, 6λ – 1, 2λ – 1).
The equation of the line passing through points C (3, 9, 4) and D (-4, 4, 4) is:
$\frac{x-3}{-4-3}=\frac{y-9}{4-9}=\frac{z-4}{4-4}$
, where x₁ = 3, y₁ = 9, z₁ = 4; and x₂ = -4, y₂ = 4, z₂ = 4
$\frac{x-3}{-7}=\frac{y-9}{-5}=\frac{z-4}{0}$
Let
$L_{2}:\frac{x-3}{-7}=\frac{\left (y-9 \right )}{-5}=\frac{z-4}{0}=\mu$
$\Rightarrow \frac{x-3}{-7}=\mu,\frac{\left (y-9 \right )}{-5}=\mu,\frac{z-4}{0}=\mu$
We must find the values of x, y, and z. Therefore,
$Take \, \frac{x-3}{-7}=\mu\\ \Rightarrow x-3=-7\mu\\ \Rightarrow x=-7\mu+3\\ \\ Take \,\frac{\left (y-9 \right )}{-5}=\mu \\ \Rightarrow y-9=-5\mu\\ \Rightarrow y=-5\mu+9\\ \\ Take\frac{z-4}{0}=\mu \\ \Rightarrow z-4=0\\ \Rightarrow z=4$
This implies that any point on line L₂ is (-7μ +3, -5μ + 9, 4).
If the lines intersect, then there must exist a value of λ and for μ, for which
$\left (4\lambda, 6\lambda - 1, 2\lambda -1\right) \equiv \left(-7\mu + 3, -5\mu + 9, 4\right ) \\ \Rightarrow 4\lambda = -7\mu + 3...(i)\\ 6\lambda - 1 = -5\mu + 9..(ii)\\ 2\lambda - 1 = 4 �(iii)\\$
From equation (iii), we get
$2\lambda - 1 = 4 \\ \Rightarrow 2\lambda=4+1\\ \Rightarrow 2\lambda=5\\ \Rightarrow \lambda=\frac{5}{2}$
Substituting the value of λ in equation (i),
$4\left ( \frac{5}{2} \right )=-7\mu+3\\ \Rightarrow 2 \times 5=-7\mu+3\\ \Rightarrow 10=-7\mu+3\\ \Rightarrow 7\mu=3-10\\ \Rightarrow 7\mu=-7 \\ \Rightarrow -\frac{7}{7}\\ \Rightarrow \mu=-1$
Substituting these values of λ and μ in equation (ii),
$6\left ( \frac{5}{2} \right )-1=-5\left ( -1 \right )+9\\ \Rightarrow 3 \times 5 - 1 = 5 + 9\\ \Rightarrow 15 - 1 = 14\\ \Rightarrow 14 = 14$
Since the values of λ and μ satisfy eq (ii), the lines intersect.
Hence, proved that the line through A and B intersects the line through C and D.

Question:6

Prove that lines x = py + q, z = ry + s, and x = p’y + q’, z = r’y + s’ are perpendicular if pp’ + rr’ + 1 = 0.

Answer:

Given: x = py + q, z = ry + s, and x = p’y + q’, z = r’y + s’ are perpendicular.
To Prove: pp’ + rr’ + 1 = 0.
Proof:
Let us take x = py + q and z = ry + s.
From x = py + q;
py = x - q
$\Rightarrow y=\frac{x-q}{p}$
From z = ry + s;
ry = z - s
$\Rightarrow y=\frac{z-s}{r}$
So, $\frac{x-q}{p}=y=\frac{z-s}{r}$
$\frac{x-q}{p}=\frac{y}{1}=\frac{z-s}{r}$ Or, … (i)
Now, if we take x = p’y + q’ and z = r’y + s’
From x = p’y + q’;
p’y = x - q’
$\Rightarrow y=\frac{x-{q}'}{{p}'}$
From z = r’y + s’;
r’y = z - s’
$\Rightarrow y=\frac{z-{s}'}{{r}'}$
So,
$\frac{x-{q}'}{{p}'}=y=\frac{z-{s}'}{{r}'}$
Or,
$L_{2}:\frac{x-{q}'}{{p}'}=\frac{y}{1}=\frac{z-{s}'}{{r}'}.......(ii)$
From (i),
Line L₁ is parallel to $p\hat{i}+\hat{j}+r\hat{k}$ (from the denominators of the equation (i))
From (ii),
Line L₂ is parallel to ${p}'\hat{i}+\hat{j}+{r}'\hat{k}$ (from the denominators of the equation (ii))
According to the question, L₁ and L₂ are perpendicular.
Therefore, the dot product of the vectors should equate to 0.
Or,
$\left (p\hat{i}+\hat{j}+r\hat{k} \right ).\left ({p}'\hat{i}+\hat{j}+{r}'\hat{k} \right )\\ \Rightarrow p{p}'+1+r{r}'=0$
(since, in vector dot product, $\left (x\hat{i}+y\hat{j}+z\hat{k} \right )\left ({x}'\hat{i}+{y}'\hat{j}+{z}'\hat{k} \right )= x{x}'+y{y}'+z{z}'=0$
Or,
$p{p}'+r{r}'+1=0$
Therefore, the lines are perpendicular if pp’ + rr’ + 1 = 0.

Question:7

Find the equation of a plane which bisects perpendicularly the line joining A (2, 3, 4) and B (4, 5, 8) at right angles.

Answer:

Given, there exists a plane which perpendicularly bisects the line joining A (2, 3, 4) and B (4, 5, 8) at right angles. We must find the equation of this plane.
First, let us find the midpoint of AB.
Since the midpoint of any line is halfway between the two end points,
$Midpoint \: of \: AB=\left ( \frac{2+4}{2},\frac{3+5}{2},\frac{4+8}{2} \right )$
$Midpoint \: of \: AB=\left ( \frac{6}{2},\frac{8}{2},\frac{12}{2} \right )$
= (3, 4, 6).
We can represent this as a position vector, $\vec{a}=3\hat{i}+4\hat{j}+6\hat{k}$
Next, we must find the normal of the plane, $\vec{n}$
$\vec{n}=\left ( 4-2 \right )\hat{i}+\left ( 5-3 \right )\hat{j}+\left ( 8-4 \right )\hat{k}\\ \Rightarrow \vec{n}=2\hat{i}+2\hat{j}+4\hat{k}$
We know, the equation of the plane which perpendicularly bisects the line joining two given points is
$\left ( \vec{r}-\vec{a} \right )\vec{n}=0$
Where,
$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$
Substituting the values in the above equation,
$\left (\left (x\hat{i}+y\hat{j}+z\hat{k} \right ) -\left (3\hat{i}+4\hat{j}+6\hat{k} \right ) \right ).\left (2\hat{i}+2\hat{j}+4\hat{k} \right )=0\\ \Rightarrow \left ( x\hat{i}+y\hat{j}+z\hat{k}-3\hat{i}-4\hat{j}-6\hat{k} \right ).\left (2\hat{i}+2\hat{j}+4\hat{k} \right )=0\\\Rightarrow \left ( x\hat{i}-3\hat{i}+y\hat{j}-4\hat{j}+z\hat{k}-6\hat{k} \right ).\left (2\hat{i}+2\hat{j}+4\hat{k} \right )=0\\\Rightarrow \left ( (x-3)\hat{i}+(y-4)\hat{j}+(z-6)\hat{k} \right ).\left (2\hat{i}+2\hat{j}+4\hat{k} \right )=0\\\Rightarrow 2\left ( x-3 \right )+2(y-4)+4(z-6)=0$
Upon further simplification,
$\Rightarrow 2x-6+2y-8+4z-24=0\\ \Rightarrow 2x+2y+4z-6-8-24=0\\ \Rightarrow 2x+2y+4z-38=0\\ \Rightarrow 2\left ( x+y+2z-19 \right )=0\\ \Rightarrow x+y+2z-19=0\\ \Rightarrow x+y+2z=19$
Therefore, the required equation of the plane is x + y + 2z = 19.

Question:8

Find the equation of a plane which is at a distance $3\sqrt{3}$ units from the origin and the normal to which is equally inclined to coordinate axes.

Answer:

Given, the plane is at a distance of $3\sqrt{3}$ from the origin, and the normal is equally inclined to coordinate axes.
We need to find the equation of this plane.
We know, the vector equation of a plane located at a distance d from the origin is represented by:
$\vec{r}.\hat{n}=d\\ \Rightarrow \left ( x\hat{i}+y\hat{j}+z\hat{k} \right ).\left ( l\hat{i}+m\hat{j}+n\hat{k} \right )=d$
lx + my + nz = d ….(i) , where l, m and n are the direction cosines of the normal of the plane.
Since the normal is equally inclined to the coordinate axes,
$l = m = n \\ \cos \alpha =\cos\beta =\cos \gamma �(ii)$
Also, we know,
$\cos^{2} \alpha =\cos^{2}\beta =\cos^{2} \gamma=1\\ \Rightarrow \cos^{2} \alpha =\cos^{2}\alpha =\cos^{2} \alpha =1 \: \: \left ( from(ii) \right )\\ \Rightarrow 3\cos^{2}\alpha=1\\ \Rightarrow \cos^{2}\alpha=\frac{1}{3}\\ \Rightarrow \cos \alpha =\frac{1}{\sqrt{3}}$
This means, $l=m=n =\frac{1}{\sqrt{3}}$
if we substitute the values of l, m and n in equation (i),
$\left (\frac{1}{\sqrt{3}} \right )x+\left (\frac{1}{\sqrt{3}} \right )y+\left (\frac{1}{\sqrt{3}} \right )z=d\: \: \left [where\: d=3\sqrt{3} \right ]$
So,
$\left (\frac{1}{\sqrt{3}} \right )x+\left (\frac{1}{\sqrt{3}} \right )y+\left (\frac{1}{\sqrt{3}} \right )z=3\sqrt{3} \\ \Rightarrow \frac{x+y+z}{\sqrt{3}}=3\sqrt{3}\\ \Rightarrow x+y+z=3\sqrt{3}\times \sqrt{3}\\ \Rightarrow x+y+z=3 \times 3=9$
Therefore, the required equation of the plane is x + y + z = 9.

Question:9

. If the line drawn from the point (-2, -1, -3) meets a plane at right angle at the point (1, -3, 3), find the equation of the plane.

Answer:

Given: the line drawn from point (-2, -1, -3) meets a plane at 90⁰ at the point (1, -3, 3). We must find the equation of the plane.
Any line perpendicular to the plane is the normal.
Let the points be P (-2, -1, -3) and Q (1, -3, 3), then the line PQ is a normal to the plane.
Hence, PQ = (1 + 2, -3 + 1, 3 + 3)=> PQ = (3, -2, 6)
=> Normal to the plane = $\vec{PQ}$
$\vec{PQ}=3\hat{i}-2\hat{j}+6\hat{k}$
The vector equation of a plane is represented by $\left (\vec{r}-\vec{a} \right ).\vec{n}=0$
Putting the obtained values in this equation,
$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\\ \vec{a}=\hat{i}-3\hat{j}+3\hat{k}\\ \vec{n}=3\hat{i}-2\hat{j}+6\hat{k}$
We get,
$\Rightarrow \left (\left (x\hat{i}+y\hat{j}+z\hat{k} \right )-\left (\hat{i}-3\hat{j}+3\hat{k} \right ) \right ).\left ( 3\hat{i}-2\hat{j}+6\hat{k} \right )=0\\ \Rightarrow \left ( x\hat{i}-y\hat{j}+z\hat{k}-\hat{i}+3\hat{j}-3\hat{k} \right ).\left ( 3\hat{i}-2\hat{j}+6\hat{k} \right )=0\\ \Rightarrow \left ( x\hat{i}-\hat{i}+y\hat{j}+3\hat{j}+z\hat{k}-3\hat{k} \right ).\left (3\hat{i}-2\hat{j}+6\hat{k} \right )=0\\ \Rightarrow \left ((x-1)\hat{i}+(y+3)\hat{j}+(z-3)\hat{k} \right ).\left (3\hat{i}-2\hat{j}+6\hat{k} \right )=0$
$\Rightarrow 3(x - 1) + (-2)(y + 3) + 6(z - 3) = 0\\ \Rightarrow3(x - 1) - 2(y + 3) + 6(z - 3) = 0\\ \Rightarrow 3x- 3 -2y - 6 + 6z - 18 = 0\\ \Rightarrow 3x - 2y +6z - 3 - 6 - 18 = 0\\ \Rightarrow 3x - 2y + 6z - 9 - 18 = 0\\ \Rightarrow 3x - 2y + 6z - 27 = 0\\ \Rightarrow 3x - 2y + 6z = 27$
Therefore, the required equation of the plane is 3x - 2y + 6z = 27.

Question:10

Find the equation of the plane through the points (2, 1, 0), (3, -2, -2) and (3, 1, 7).

Answer:

Given points are (2, 1, 0), (3, -2, -2), and (3, 1, 7).
We know, equation of a line passing through 3 non-collinear points (x₁ , y₁ , z₁ ), (x₂ , y₂ , z₂ ) and (x₃ , y₃ , z₃ ) is given as:
$\begin{vmatrix} x-x_{1} &y-y_{1} &z-z_{1} \\ x_{2}-x_{1}&y_{2}-y_{1} &z_{2}-z_{1} \\ x_{3}-x_{1}&y_{3}-y_{1} &z_{3}-z_{1} \end{vmatrix}=0$
Where, (x₁ , y₁ , z₁ ) = (2, 1, 0)
(x₂ , y₂ , z₂ ) = (3, -2, -2)
(x₃ , y₃ , z₃ ) = (3, 1, 7)
Therefore, x₁ = 2, y₁ = 1, z₁ = 0; x₂ = 3, y₂ = -2, z₂ = -2; x₃ = 3, y₃ = 1, z₃ = 7
Substituting these values in the line equation,
$\begin{vmatrix} x-2 &y-1 &z-0 \\ 3-2&-2-1 &-2-0 \\ 3-2&1-1 &7-0 \end{vmatrix}=0\\ \\ \\ \begin{vmatrix} x-2 &y-1 &z-0 \\ 1&-3 &-2 \\ 1&0 &7 \end{vmatrix}=0$
$\\ \\ \begin{vmatrix} x-2 &y-1 &z-0 \\ 1&-3 &-2 \\ 1&0 &7 \end{vmatrix}=\left ( x-2 \right )\left ( \left ( -3 \times 7 \right )-\left ( -2 \times 0 \right ) \right )$

$\begin{vmatrix} x-2 & y-1 &z \\ 1& -3& -2\\ 1& 0& 7 \end{vmatrix}=\left ( x-2 \right )\left ( -21-0 \right )-\left ( y-1 \right )\left ( 7-(-2) \right )+z\left ( 0-(-3) \right )$
$\begin{vmatrix} x-2 & y-1 &z \\ 1& -3& -2\\ 1& 0& 7 \end{vmatrix}=\left ( x-2 \right )\left ( -21 \right )-\left ( y-1 \right )\left ( 7+2 \right )+z\left ( 0+3 \right )$
$\begin{vmatrix} x-2 & y-1 &z \\ 1& -3& -2\\ 1& 0& 7 \end{vmatrix}=-21\left ( x-2 \right )-9\left ( y-1 \right )+3z$
$\begin{vmatrix} x-2 & y-1 &z \\ 1& -3& -2\\ 1& 0& 7 \end{vmatrix}=-21x+42-9y+9+3z$
$\begin{vmatrix} x-2 & y-1 &z \\ 1& -3& -2\\ 1& 0& 7 \end{vmatrix}=-21x-9y+3z+42+9$
$\begin{vmatrix} x-2 & y-1 &z \\ 1& -3& -2\\ 1& 0& 7 \end{vmatrix}=-21x-9y+3z+51$
Now, since
$\begin{vmatrix} x-2 & y-1 &z \\ 1& -3& -2\\ 1& 0& 7 \end{vmatrix}=0$
$\Rightarrow -21x -9y + 3z + 51 = 0\\ \Rightarrow -21x - 9y + 3z = -51\\ \Rightarrow -3(7x + 3y - z) = -3 \times 17\\ \Rightarrow 7x + 3y - z = 17$
Hence, the required equation of the plane is 7x + 3y - z = 17.

Question:11

Find the equations of the 2 lines through the origin which intersect the line $\frac{x-3}{2}=\frac{y-3}{1}=\frac{z}{1}$ at angles of $\frac{\pi}{3}$ each.

Answer:

Given the equation of the line, we need to find the equations of two lines through the origin which intersect the given line.
According to the theorem, equation of a line with direction ratios d₁ = (b₁ , b₂ , b₃ ) that passes through the point (x₁ , y₁ , z₁ ) is expressed as:
$\frac{x-x_{1}}{b_{1}}=\frac{y-y_{1}}{b_{2}}=\frac{z-z_{1}}{b_{3}}$
We also know, the angle between two lines with direction ratios d₁ and d₂ respectively is given by:
$\theta = \cos^{-1}\left ( \frac{d_{1}d_{2}}{\left |d_{1} \right |\left |d_{2} \right |} \right )$
We use these theorems to find the equations of the two lines.
Let the equation of a line be:
$\theta = \cos^{-1}\left ( \frac{d_{1}d_{2}}{\left |d_{1} \right |\left |d_{2} \right |} \right )$
Given that it passes through the origin, (0, 0, 0)
Therefore, equation of both lines passing through the origin will be :
$\frac{x}{b_{1}}=\frac{y}{b_{2}}=\frac{z}{b_{3}}=\lambda \, \, .....(i)$
Let,
$\frac{x-3}{2}=\frac{y-3}{1}=\frac{z}{1}=\mu \, \, .....(ii)$
Direction ratio of the line = (2, 1, 1)
$\Rightarrow d_{1} = (2, 1, 1).... (iii)$
If we represent the direction ratio in terms of a position vector,
$d_{1}=2\hat{i}+\hat{j}+\hat{k} .....(iv)$

Any point on the line is given by (x, y, z). From (ii),
$\frac{x-3}{2}=\mu, \frac{y-3}{1}=\mu ,\frac{z}{1}=\mu$
$\\\text{take} \ \frac{x-3}{2}=\mu\\ \Rightarrow x-3=2\mu\\ \Rightarrow x=2\mu+3\\ \\ take \frac{y-3}{1}=\mu \\ \Rightarrow y-3=\mu\\ \Rightarrow y=\mu+3\\ \\ take \frac{z}{1}=\mu\\ \Rightarrow z=\mu$
Hence, any point on line (ii) is $P(2\mu + 3, \mu + 3, \mu)$
Since line (i) passes through the origin, we can say
$\left ( b_{1},b_{2},b_{3} \right )\equiv (2\mu + 3, \mu + 3, \mu)$
$\Rightarrow \: direction\: \: ratio\: of\; line(i)= (2\mu + 3, \mu + 3, \mu)\\ \Rightarrow d_{2}= (2\mu + 3, \mu + 3, \mu)....(v)$
We can represent the direction ratio in terms of position vector like:
$d_{2}= \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \: \: ....(vi)$
From the theorem, we know
$\cos \theta=\frac{d_{1}.d_{2}}{\left |d_{1} \right |\left |d_{2} \right |}$
If we substitute the values of d? and d? from (iv) and (vi) in the above equation, and putting $\theta=\frac{\pi}{3}$ from the question:
$\Rightarrow \cos \frac{\pi}{3}=\frac{\left ( 2\hat{i}+\hat{j}+\hat{k} \right )\left ( \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right )}{\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |}$
Solving the numerator,
$\left ( 2\hat{i}+\hat{j}+\hat{k} \right )\left ( \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right )= 2\left (2\mu + 3 \right )+1\left ( \mu + 3 \right )+1. \mu$
$\left ( 2\hat{i}+\hat{j}+\hat{k} \right )\left ( \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right )= 4\mu + 6+\mu + 3+ \mu$
$\left ( 2\hat{i}+\hat{j}+\hat{k} \right )\left ( \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right )= 4\mu +\mu + \mu+6+3$
$\left ( 2\hat{i}+\hat{j}+\hat{k} \right )\left ( \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right )= 6\mu+9$
Solving the denominator,
$\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |=\sqrt{2^{2}+1^{2}+1^{2}}\sqrt{ \left (2\mu + 3 \right )^{2}+\left ( \mu + 3 \right )^{2}+ \mu^{2}}$
$\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |=\sqrt{4+1+1}\sqrt{ \left (2\mu \right )^{2}+ 3^{2}+2\left ( 2\mu \right )\left ( 3 \right )+\left ( \mu \right )^{2}+3^{2}+ 2(\mu)(3)+\mu^{2}}$
$\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |=\sqrt{6}\sqrt{4\mu^{2}+9+12\mu+u^{2}+9+6\mu+\mu^{2}}$
$\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |=\sqrt{6}\sqrt{4\mu^{2}+u^{2}+\mu^{2}+12\mu+6\mu+9+9}$
$\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |=\sqrt{6}\sqrt{6\mu^{2}+18\mu+18}$
$\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |=\sqrt{6}\sqrt{6\left (\mu^{2}+3\mu+3 \right )}$
$\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |=\sqrt{6}\sqrt{6}\sqrt{\mu^{2}+3\mu+3}$
$\left | 2\hat{i}+\hat{j}+\hat{k} \right |\left | \left (2\mu + 3 \right )\hat{i}+\left ( \mu + 3 \right )\hat{j}+ \mu\hat{k} \right |=6\sqrt{\mu^{2}+3\mu+3 }$
And cos π/3 = 1/2
Substituting the values, we get
$\Rightarrow \frac{1}{2}=\frac{6\mu+9}{6\sqrt{\mu^{2}+3\mu+3}}$
Performing cross multiplication,
$\Rightarrow 6\sqrt{\mu^{2}+3\mu+3}=2\left (6\mu+9 \right )\\ \Rightarrow 6\sqrt{\mu^{2}+3\mu+3}=2 \times 3\left (2\mu+3 \right )\\ \Rightarrow 6\sqrt{\mu^{2}+3\mu+3}=6\left (2\mu+3 \right )\\ \Rightarrow \sqrt{\mu^{2}+3\mu+3}=2\mu+3$
Squaring both sides,
$\Rightarrow \left (\sqrt{\mu^{2}+3\mu+3} \right )^{2}=\left (2\mu+3 \right )^{2}\\ \Rightarrow \mu^{2}+3\mu+3=(2\mu)^{2}+3^{2}+2(2\mu)(3)\left [ \because (a+b)^{2}=a^{2}+b^{2}+2ab \right ]\\ \Rightarrow \mu^{2}+3\mu+3=4\mu^{2}+9+12\mu\\ \Rightarrow 4\mu^{2}-\mu^{2}+12\mu-3\mu+9-3=0\\ \Rightarrow 3\mu^{2}+9\mu+6=0$
$\Rightarrow 3\left ( \mu^{2}+3\mu+2 \right ) =0\\ \Rightarrow \mu^{2}+3\mu+2=0\\ \Rightarrow\mu^{2}+2\mu+\mu+2=0\\ \Rightarrow \mu\left ( \mu+2 \right )+\left ( \mu+2 \right )=0\\ \Rightarrow \left ( \mu+1 \right )+\left ( \mu+2 \right )=0\\$
$\Rightarrow \left ( \mu+1 \right )=0 \: \: or\: \left ( \mu+2 \right )=0\\ \Rightarrow \mu=-1 \: \: \: or\: \: \: \mu=-2$
Therefore, from equation (v)
Direction ratio = $(2\mu+ 3, \mu + 3, \mu)$
Putting μ = -1:
Direction Ratio = (2(-1) + 3, (-1) + 3, -1)
⇒ Direction Ratio = (-2 + 3, -1 + 3, -1)
⇒ Direction Ratio = (1, 2, -1) …(vi)
Now putting μ = -2:
Direction Ratio = (2(-2) + 3, (-2) + 3, -2)
⇒ Direction Ratio = (-4 + 3, -2 + 3, -2)
⇒ Direction Ratio = (-1, 1, -2) …(vii)
Using the direction ratios in (vi) and (vii) in equation (i);
$\frac{x}{b_{1}}=\frac{y}{b_{2}}=\frac{z}{b_{3}}=\lambda\\ \\ \\ \frac{x}{1}=\frac{y}{2}=\frac{z}{-1}=\lambda$
And,
$\frac{x}{-1}=\frac{y}{1}=\frac{z}{-2}=\lambda$
Therefore, the two required lines are $\frac{x}{1}=\frac{y}{2}=\frac{z}{-1}=\lambda$ and $\frac{x}{-1}=\frac{y}{1}=\frac{z}{-2}=\lambda$

Question:12

Find the angle between the lines whose direction cosines are given by equations l + m + n = 0, l² + m² - n² = 0.

Answer:

Given, two lines whose direction cosines are l + m + n = 0 - (i); and l² + m² - n² = 0 - (ii). We need to find the angle between these lines.
First, we must find the values of l, m and n.
From equation (i), l + m + n = 0
=> n = - l - m
=> n = -(l + m) …(iii)
If we substitute the value of n from (i) in (ii),
$l^{2}+m^{2}-n^{2}=0\\ \Rightarrow l^{2}+m^{2}-\left (-\left ( l+m \right ) \right )^{2}=0\\ \Rightarrow l^{2}+m^{2}-\left ( l+m \right ) ^{2}=0\\ \Rightarrow l^{2}+m^{2}-\left ( l^{2}+m^{2}+2lm \right )=0\\ \Rightarrow l^{2}+m^{2} -l^{2}-m^{2}-2lm=0\\ \Rightarrow l^{2}-l^{2}+m^{2}-m^{2}-2lm=0\\ \Rightarrow -2lm=0\\ \Rightarrow lm=0$
⇒ l = 0 or m = 0
Putting l = 0 in equation (i),
=> 0 + m + n = 0
=> m + n = 0
=> m = -n
If m = $\lambda$ , then
n = -m = - $\lambda$
Hence, direction ratios (l, m, n) = (0, $\lambda$ , - $\lambda$ )
=> Position vector parallel to these given lines = $0\hat{i}+\lambda\hat{j}-\lambda \hat{k}$
$\Rightarrow d_{1}=\lambda\hat{j}-\lambda \hat{k}$
Now, putting m = 0 in equation (i),
=> l + 0 + n = 0
=> l + n = 0
=> l = -n
If n = $\lambda$ , then
l = -n = - $\lambda$
Hence, direction ratios (l, m, n) = (- $\lambda$ , 0, $\lambda$ )
=> Position vector parallel to these given lines = $-\lambda \hat{i}+\0\hat{j}+\lambda \hat{k}$
$\Rightarrow d_{2}=-\lambda\hat{i}+\lambda \hat{k}$
From the theorem, we get the angle between the two lines whose direction ratios are d₁ and d₂ as:
$\theta=\cos^{-1}\left ( \frac{\left | d_{1}.d_{2} \right |}{\left | d_{1}\right |\left |d_{2} \right |} \right )$
If we substitute the values of d₁ and d₂, we get
$\theta=\cos^{-1}\left ( \frac{\left| \left ( \lambda \hat{j}-\lambda \hat{k} \right )\left (- \lambda \hat{i}+\lambda \hat{k} \right ) \right |}{\left | \left ( \lambda \hat{j}-\lambda \hat{k} \right )\right |\left |\left (- \lambda \hat{i}+\lambda \hat{k} \right ) \right |} \right )$
Solving the numerator,
$\left ( \lambda \hat{j}-\lambda \hat{k} \right )\left (- \lambda \hat{i}+\lambda \hat{k} \right ) =0+0+\left ( -\lambda \right )\left ( \lambda \right )\\ \Rightarrow \left ( \lambda \hat{j}-\lambda \hat{k} \right )\left (- \lambda \hat{i}+\lambda \hat{k} \right )= -\lambda^{2}$
Solving the denominator,
$\left |\left ( \lambda \hat{j}-\lambda \hat{k} \right ) \right |\left |\left (- \lambda \hat{i}+\lambda \hat{k} \right ) \right |=\sqrt{ \lambda ^{2}\left (-\lambda \right )^{2}} \sqrt{\left (- \lambda \right )^{2}+\lambda ^{2}}$
$\left |\left ( \lambda \hat{j}-\lambda \hat{k} \right ) \right |\left |\left (- \lambda \hat{i}+\lambda \hat{k} \right ) \right |=\sqrt{ \lambda ^{2}+\lambda^{2}} \sqrt{ \lambda^{2}+\lambda ^{2}}$
$\left |\left ( \lambda \hat{j}-\lambda \hat{k} \right ) \right |\left |\left (- \lambda \hat{i}+\lambda \hat{k} \right ) \right |= \lambda ^{2}+\lambda^{2}$
$\left |\left ( \lambda \hat{j}-\lambda \hat{k} \right ) \right |\left |\left (- \lambda \hat{i}+\lambda \hat{k} \right ) \right |=2 \lambda ^{2}$
Substituting the values in θ,
$\theta=\cos^{-1}\left ( \frac{\left | -\lambda^{2} \right |}{\lambda^{2}} \right )\\ \Rightarrow \theta=\cos^{-1}=\frac{1}{2}\\ \Rightarrow \theta=\frac{\pi}{3}\left [ \because \cos\frac{\pi}{3}=\frac{1}{2} \right ]$
Therefore, the required angle between the lines is π/3.

Question:13

If a variable line in two adjacent positions has direction cosines l, m, n and $l+\delta l,\: m+\delta m,\: n+\delta n,$ show that the small angle $\delta \theta$ between the two positions is given by $\delta \theta^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$

Answer:

Given: direction cosines of a variable line in two adjacent positions are l, m, n and $l+\delta l, m+\delta m,n+\delta n,$
We have to prove that the small angle $\delta \theta$ between the two positions is given by $\delta \theta^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}$
We know, the relationships between direction cosines is given as
$l^{2}+ m^{2}+ n^{2}=1 ....(1)$
Also, $\left (l+\delta l \right )^{2}+ \left (m+\delta m \right )^{2}+ \left (n+\delta n \right )^{2}=1$
$\Rightarrow l^{2}+(\delta l)^{2}+2(l)(\delta l)+m^{2}+(\delta m)^{2}+2(m)(\delta m)+n^{2}+(\delta n)^{2}+2(n)(\delta n)=1\\ \Rightarrow l^{2}+m^{2}+n^{2}+\left (\delta l \right )^{2}+\left (\delta m \right )^{2}+\left (\delta n \right )^{2}+2l\delta l+2m\delta m+2n\delta n=1\\ \Rightarrow 1+\delta l^{2}+\delta m^{2}+ \delta n^{2}+2l\delta l+2m\delta m+2n\delta n=1\: \: \: \left [ from (i) \right ] \\ \Rightarrow 2l\delta l+2m\delta m+2n\delta n+\delta l^{2}+\delta m^{2}+ \delta n^{2}=1-1 \\ \Rightarrow 2 \left (l\delta l+m\delta m+n\delta n \right )=-\left (\delta l^{2}+\delta m^{2}+ \delta n^{2} \right )\\ \Rightarrow l\delta l+m\delta m+n\delta n =-\frac{1}{2}\left (\delta l^{2}+\delta m^{2}+ \delta n^{2} \right ).......(iii)$
Let
$\vec{a}=l\hat{i}+m\hat{j}+n\hat{k}\\ \Rightarrow \vec{b}=\left ( l+\delta l \right )\hat{i}+\left ( m+\delta m \right )\hat{j}+\left ( n+\delta n \right )\hat{k}$
We know, angle between two lines = $\cos \theta=\vec{a}. \vec{b}$
Here, the angle is very small because the line is variable in different although adjacent positions. According to the question, this small angle is $\delta \theta$
Therefore,
$\cos \delta \theta=\vec{a}. \vec{b}$
Substituting the values of the two vectors, we get
$\Rightarrow \cos \delta \theta = \left (l\hat{i}+m\hat{j}+n\hat{k} \right ).\left (\left ( l+\delta l \right )\hat{i}+\left ( m+\delta m \right )\hat{j}+\left ( n+\delta n \right )\hat{k} \right )$
The dot product of 2 vectors is calculated by obtaining the sum of the product of the coefficients of $\hat{i},\hat{j}\; and \; \hat{k}$
$\Rightarrow \cos \delta \theta =l \left ( l+\delta l \right )+m \left ( m+\delta m \right )+n \left ( n+\delta n \right )\\ \Rightarrow \cos \delta \theta = l^{2}+l \delta l+m^{2}+m \delta m+n^{2}+n \delta n\\ \Rightarrow \cos \delta \theta =l^{2}+m^{2}+n^{2}+l \delta l+m \delta m+n \delta n\\ \Rightarrow \cos \delta \theta =1+l \delta l+m \delta m+n \delta n\: \: \left [ from(i) \right ]\\ \Rightarrow \cos \delta \theta=1-\frac{1}{2}\left ( \delta l^{2}+\delta m^{2}+\delta n^{2} \right )\: \: \: \: \left [ \because from(ii) \right ]\\ \Rightarrow \frac{1}{2}\left ( \delta l^{2}+\delta m^{2}+\delta n^{2} \right )=1-\cos \delta \theta$
Or,
$\Rightarrow 1-\cos \delta \theta= \frac{1}{2}\left ( \delta l^{2}+\delta m^{2}+\delta n^{2} \right )$
We know, $1 -\cos 2 \theta = 2\sin^{2} \theta$
On the left-hand side, the angle is $2 \theta$ . On the right hand side, it becomes half, that is, $\frac{ 2 \theta}{2} =\theta$ .
Similarly replacing $2 \theta$ by $\delta \theta$ in LHS, then making the angle on the RHS half,
We get:
$1 -\cos \delta \theta = 2\sin^{2} \frac{\delta \theta}{2}$
$\Rightarrow 2\sin^{2} \frac{\delta \theta}{2}=\frac{1}{2}\left ( \delta l^{2}+\delta m^{2}+\delta n^{2} \right )\\ \Rightarrow 2 \times 2\sin^{2} \frac{\delta \theta}{2}= \delta l^{2}+\delta m^{2}+\delta n^{2} \\ \Rightarrow 4\sin^{2} \frac{\delta \theta}{2}= \delta l^{2}+\delta m^{2}+\delta n^{2} \\ \Rightarrow 4\left ( \sin \frac{\delta \theta}{2} \right )^{2}= \delta l^{2}+\delta m^{2}+\delta n^{2} \\$
Since $\delta \theta$ is a very small angle, $\frac{\delta \theta}{2}$ will be much smaller. Hence $\sin \frac{\delta \theta}{2}$ will also be very small in value.
$\Rightarrow \sin \frac{\delta \theta}{2}=\frac{\delta \theta}{2}\\ \\ \Rightarrow 4\left ( \frac{\delta \theta}{2} \right )^{2}=\delta l^{2}+\delta m^{2}+\delta n^{2}\\ \Rightarrow 4 \frac{\delta \theta^{2}}{4} =\delta l^{2}+\delta m^{2}+\delta n^{2}\\ \\ \Rightarrow \delta \theta^{2} =\delta l^{2}+\delta m^{2}+\delta n^{2}\\$
Hence, proved.

Question:14

O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of the plane through A at right angle to OA.

Answer:

We have the points O (0, 0, 0) and A (a, b, c) where a, b, and c are direction ratios. We need to find the direction cosines of line OA and the equation of the plane through A at right angle to OA.
To begin with,
$\vec{OA}=Position\: vector\: of\: A-Position\: vector\: of\:O\\ \Rightarrow \vec{OA}=\left ( a\hat{i}+b\hat{j}+c\hat{k} \right )-\left ( 0\hat{i}+0\hat{j}+0\hat{k} \right ) \\ \Rightarrow \vec{OA}= a\hat{i}-0\hat{i}+b\hat{j}-0\hat{j}+c\hat{k}-0\hat{k}\\ \Rightarrow \vec{OA}= a\hat{i}+b\hat{j}+c\hat{k}$
We know, if (a, b, c) are the direction ratios of a given vector, then its direction cosines will be:
$\left ( \frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}},\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}},\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} \right )$
According to the question, the direction ratios are (a, b, c), therefore the direction cosines of the vector OA are the same as the above formula, that is,
$\left ( \frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}},\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}},\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}} \right )$
Given, the plane is perpendicular to OA. We know, a normal is a line or vector which is perpendicular to a given object. Therefore, we can say:
$\vec{n}=\vec{OA}\\ \Rightarrow \vec{n}=a\hat{i}+b\hat{j}+c\hat{k}\\ \left [ \because \vec{OA}=a\hat{i}+b\hat{j}+c\hat{k} \right ]$
Also, the vector equation of a plane where the normal is passing through the plane and passing through is,
$\left ( \vec{r}-\vec{a} \right ).\vec{n}=0$
Where
$\vec{r}-\vec{a} = vector\: from\: \vec{A}\: to\: \vec{R} \\ \vec{a}=Position\: vector\: of\: the\: given\: point\: in\: the\: plane\\ \vec{n}=normal\: vector\: to\: the\: plane$
Here, the given point in the plane is A (a, b, c).
$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\\ \vec{a}=a\hat{i}+b\hat{j}+c\hat{k}\\ \vec{n}=a\hat{i}+b\hat{j}+c\hat{k}\\$
Substituting the vectors respectively, we get:
$\left (\left (x\hat{i}+y\hat{j}+z\hat{k} \right )-\left (a\hat{i}+b\hat{j}+c\hat{k} \right ) \right ).\left (a\hat{i}+b\hat{j}+c\hat{k} \right )=0\\ \Rightarrow \left (x\hat{i}+y\hat{j}+z\hat{k} -a\hat{i}-b\hat{j}-c\hat{k} \right ).\left (a\hat{i}+b\hat{j}+c\hat{k} \right )=0\\ \Rightarrow \left (\left (x-a \right )\hat{i}+\left (y-b \right )\hat{j}+\left (z-c \right )\hat{k}\right ).\left (a\hat{i}+b\hat{j}+c\hat{k} \right )=0\\ \Rightarrow a\left (x-a \right )+b\left (y-b \right )+c\left (z-c \right )=0\\$
Upon simplifying this, we get:
$\Rightarrow ax - a^{2} + by-b^{2} + cz - c^{2} =0\\ \Rightarrow ax + by + cz - a^{2}-b^{2}- c^{2} =0\\ \Rightarrow a^{2}+b^{2}+ c^{2} =ax + by + cz$
Hence, the required equation of the plane is a² + b² + c² = ax + by + cz.

Question:15

Two systems of rectangular axis have the same origin. If a plane cuts them at distances a, b, c and a’, b’, c’ respectively from the origin, prove that:
$\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{a'^{2}}+\frac{1}{b'^{2}}+\frac{1}{c'^{2}}$

Answer:

Given, we have 2 systems of rectangular axes. Both the systems have the same origin, and there is a plane that cuts both systems.
One system is cut at a distance of a, b, c.
The other system is cut at a distance of a’, b’, c’.
To prove:
$\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{a'^{2}}+\frac{1}{b'^{2}}+\frac{1}{c'^{2}}$
Proof: Since a plane intersects both the systems at distances a, b, c, and a’, b’, c’ respectively, this plane will have different equations in the two different systems.
Let us consider the equation of the plane in the system with distances a, b, c to be:
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
Let us consider the equation of the plane in the system with distances a’, b’, c’ be:
$\frac{x}{a'}+\frac{y}{b'}+\frac{z}{c'}=1$
According to the question, the plane cuts both the systems from the origin. We know, the perpendicular distance of a plane $ax + by + cz + d =0$ from the origin is given by:
$\left | \frac{d}{\sqrt{a^{2}+b^{2}+c^{2}}} \right |$
(where not all a, b, and c are zero)
Therefore, the perpendicular distance from the origin of the first plane is:
$\left | \frac{-1}{\sqrt{\left (\frac{1}{a} \right )^{2}+\left (\frac{1}{b} \right )^{2}+\left (\frac{1}{c} \right )^{2}}} \right |$
And, the perpendicular distance from the origin of the second plane:
$\left | \frac{-1}{\sqrt{\left (\frac{1}{a'} \right )^{2}+\left (\frac{1}{b'} \right )^{2}+\left (\frac{1}{c'} \right )^{2}}} \right |$
We also know, if two systems of lines have the same origin, their perpendicular distances from the origin to the plane in both systems are equal.
Therefore,
$\left | \frac{-1}{\sqrt{\left (\frac{1}{a} \right )^{2}+\left (\frac{1}{b} \right )^{2}+\left (\frac{1}{c} \right )^{2}}} \right |=\left | \frac{-1}{\sqrt{\left (\frac{1}{a'} \right )^{2}+\left (\frac{1}{b'} \right )^{2}+\left (\frac{1}{c'} \right )^{2}}} \right |$
$\Rightarrow \frac{1}{\sqrt{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}}} =\frac{1}{\sqrt{\frac{1}{a'^{2}}+\frac{1}{b'^{2}}+\frac{1}{c'^{2}}}}$
Cross-multiplying,
$\Rightarrow \sqrt{\frac{1}{a'^{2}}+\frac{1}{b'^{2}}+\frac{1}{c'^{2}}}=\sqrt{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}}$
Squaring both sides,
$\Rightarrow \sqrt{\frac{1}{a'^{2}}+\frac{1}{b'^{2}}+\frac{1}{c'^{2}}}=\sqrt{\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}}$
$\Rightarrow \frac{1}{a'^{2}}+\frac{1}{b'^{2}}+\frac{1}{c'^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}$

Or
$\Rightarrow \frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{a'^{2}}+\frac{1}{b'^{2}}+\frac{1}{c'^{2}}$
Hence, proved.

Question:16

Find the foot of the perpendicular from the point (2, 3, -8) to the line $\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$
Also, find the perpendicular distance from the given point to the line.

Answer:

Given, the perpendicular from the point (let) C (2, 3, -8) to the line of which the equation is,
$\frac{4-x}{2}=\frac{y}{6}=\frac{1-z}{3}$
This can be re-written as,
$\frac{x-4}{-2}=\frac{y}{6}=\frac{z-1}{-3}$
Hence, the vector equation of the line is, $-2\hat{i}+6\hat{j}-3\hat{k}$
We must find the foot of the perpendicular from the point C (2, 3, -8) to given line, as well as the perpendicular distance from the given point C to the line.
To start with, let us locate the point of intersection between the point and the line.
Let us take,
$\frac{x-4}{-2}=\frac{y}{6}=\frac{z-1}{-3}=\lambda$
$\frac{x-4}{-2}=\lambda,\frac{y}{6}=\lambda,\frac{z-1}{-3}=\lambda$
$from\frac{x-4}{-2}=\lambda\\\Rightarrow x-4=-2\lambda \\\Rightarrow x=4-2\lambda\\ \\ from \frac{y}{6}=\lambda\\ \Rightarrow y=6\lambda\\ \\ from \frac{z-1}{-3}=\lambda\\ \Rightarrow z-1=-3\lambda\\\Rightarrow z=1-3\lambda$
We have, $x = 4 - 2\lambda , y = 6\lambda, z = 1 - 3\lambda$
Therefore, the coordinates of any point on the given line is $\left ( 4 - 2\lambda , 6\lambda, 1 - 3\lambda \right )$
a16
Let us consider the foot of the perpendicular from C(2, 3, -8) on line to be $L\left ( 4 - 2\lambda , 6\lambda, 1 - 3\lambda \right )$
Therefore, the direction ratios of $CL\left ( 4 - 2\lambda-2 , 6\lambda-3, 1 - 3\lambda-(-8) \right )$
$=\left ( 4 - 2\lambda-2 , 6\lambda-3, 1+8 - 3\lambda \right )\\ =\left ( 2-2\lambda , 6\lambda-3, 9 - 3\lambda \right )$

Also, the direction ratio of the line is, $\frac{x-4}{-2}=\frac{y}{6}=\frac{z-1}{-3}$ (-2, 6, -3).
Since L is the foot of the perpendicular on the line,
Sum of the product of these direction ratios $\left ( 2-2\lambda , 6\lambda-3, 9 - 3\lambda \right )$ and (-2, 6, -3) = 0.
$-2\left ( 2-2\lambda\right ) +6\left (6\lambda-3 \right )+(-3)\left ( 9 - 3\lambda \right )\\\\ \Rightarrow -4+4\lambda+36\lambda-18-27+9\lambda=0\\ \Rightarrow \left ( 4\lambda+36\lambda+9\lambda \right )+\left ( -4-18-27 \right )=0\\ \Rightarrow 49\lambda-49=0\\ \Rightarrow 49\lambda=49\\ \Rightarrow \lambda= \frac{49}{49}\\Hence \: \: \lambda=1$
If we substitute this value of λ in $L\left ( 4 - 2\lambda , 6\lambda, 1 - 3\lambda \right )$ , we get
$\Rightarrow L\left ( 4 - 2\lambda , 6\lambda, 1 - 3\lambda \right )=L(4 - 2(1), 6(1), 1 - 3(1))$
$\Rightarrow L\left ( 4 - 2\lambda , 6\lambda, 1 - 3\lambda \right )=L(4 - 2, 6, 1 - 3)$
$\Rightarrow L\left ( 4 - 2\lambda , 6\lambda, 1 - 3\lambda \right )=L(2, 6, -2)$
Now, we must calculate the perpendicular distance of point C from the line, that is point L.
In other words, we need to find $\left | \vec{CL} \right |$
We know, $\vec{CL} =\left ( 2-2\lambda,6\lambda-3,9-3\lambda \right )$
Substituting λ = 1,
$\vec{CL} =\left ( 2-2(1),6(1)-3,9-3(1) \right )\\ \Rightarrow \vec{CL} =\left ( 2-2,6-3,9-3 \right )\\ \Rightarrow \vec{CL} =\left ( 0,3,6 \right )$
To find $\left | \vec{CL} \right |$
$\left | \vec{CL} \right |=\sqrt{0^{2}+3^{2}+6^{2}}\\ \Rightarrow \left | \vec{CL} \right |=\sqrt{0+9+36} \Rightarrow \left | \vec{CL} \right |=\sqrt{45}\\ \Rightarrow \left | \vec{CL} \right |=3\sqrt{5}$
Therefore, the foot of the perpendicular from the point C to the given line is (2, 6, -2) and the perpendicular distance is $3\sqrt{5}$ units.

Question:17

Find the distance of a point (2, 4, -1) from the line $\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}$
Answer:

Given, the point P (2, 4, -1), the equation of the line is $\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}$
We must find the distance of point P from this line.
Note, to find the distance between a point and a line, we should get foot of the perpendicular from the point on the line.
Let, P(2, 4, -1) be the given point and be $L:\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}=\lambda$ the given line.
Direction ratio of the line L is (1, 4, -9) …(i)
Let us find any point on this line.
Taking L,
$\frac{x+5}{1}=\frac{y+3}{4}=\frac{z-6}{-9}=\lambda$
$\frac{x+5}{1}=\lambda,\frac{y+3}{4}=\lambda,\frac{z-6}{-9}=\lambda$
$Take \frac{x+5}{1}=\lambda\\ \Rightarrow x+5=\lambda\\ \Rightarrow x=\lambda - 5\\\\ Take \frac{y+3}{4}=\lambda\\ \Rightarrow y+3=4\lambda\\ \Rightarrow y=4\lambda-3\\ \\ Take \frac{z-6}{-9}=\lambda\\ \Rightarrow z-6=-9\lambda\\ \Rightarrow z=6-9\lambda$
Therefore, any point on the line L is $(\lambda - 5, 4\lambda - 3, 6 - 9\lambda)$
Let this point be $Q(\lambda - 5, 4\lambda - 3, 6 - 9\lambda)$ , the foot of the perpendicular from the point P (2, 4, -1) on the line L.
Hence, the direction ratio of PQ is given by
$(\lambda - 5-2, 4\lambda - 3-4, 6 - 9\lambda-(-1))$
=> Direction ratio of PQ= $(\lambda - 7, 4\lambda - 7, 7 - 9\lambda)$ …(ii)
Also, we know, if two lines are perpendicular to each other, then the dot product of their direction ratios should be 0.
Here, PQ is perpendicular to L. We have, from (i) and (ii),
Direction ratio of L = (1, 4, -9)
Direction ratio of PQ = $(\lambda - 7, 4\lambda - 7, 7 - 9\lambda)$
Therefore,
$(1, 4, -9).(\lambda - 7, 4\lambda - 7, 7 - 9\lambda) = 0\\ \Rightarrow 1 (\lambda- 7) + 4 (4\lambda - 7) + (-9) (7 - 9\lambda) = 0\\ \Rightarrow \lambda - 7 + 16\lambda - 28 -63 + 81\lambda = 0\\ \Rightarrow \lambda + 16\lambda + 81\lambda - 7 - 28- 63 = 0\\ \Rightarrow 98\lambda - 98 = 0\\ \Rightarrow 98\lambda = 98\\ \Rightarrow \lambda = 1$
Hence, the coordinate of Q, i.e. the foot of the perpendicular from the point on the given line is,
$Q (\lambda - 5, 4\lambda - 3, 6 - 9\lambda) = Q (1 - 5, 4(1) - 3, 6 - 9)\\ \Rightarrow Q (\lambda - 5, 4\lambda - 3, 6 - 9\lambda) = Q (1 - 5, 4 - 3, 6 - 9)\\ \Rightarrow => Q(\lambda - 5, 4\lambda - 3, 6 - 9\lambda) = (-4, 1, -3)$
Now, to find the perpendicular distance from P to the line, that is point Q,
That is, to find $\left | \vec{PQ} \right |$
We know,
$\left | \vec{PQ} \right |=(\lambda - 7, 4\lambda - 7, 7 - 9\lambda)$
Substituting $\lambda=1$
$\vec{PQ}=(1 - 7, 4(1)- 7, 7 - 9(1))\\ \Rightarrow \vec{PQ}=\left ( -6,4-7,7-9 \right )\\ \Rightarrow \vec{PQ}=\left ( -6,-3,-9 \right )$
Now, to find
$\left | \vec{PQ} \right |= \sqrt{(-6)^{2}+(-3)^{2}+(-2)^{2} }\\ \Rightarrow \left | \vec{PQ} \right |= \sqrt{36+9+4}\\ \Rightarrow \left | \vec{PQ} \right |= \sqrt{49}\\ \Rightarrow \left | \vec{PQ} \right |= 7$
Therefore, the distance from the given point to the given line = 7 units.

Question:18

Find the length and the foot of the perpendicular from the point (1, 3/2, 2) to the plane 2x - 2y + 4z + 5 = 0.

Answer:

Given, point P (1, 3/2, 2)
The plane is 2x - 2y + 4z + 5 = 0
We must find the foot of the perpendicular from the point P to the equation of the given plane.
Also, we must find the distance from the point P to the plane.
Let us consider the foot of the perpendicular from point P to be Q.
Let Q be Q (x₁ , y₁ , z₁)
So, the direction ratio of PQ is given by
(x₁ - 1, y₁ - 3/2, z₁ - 2)
Now, let us consider the normal to the plane 2x - 2y + 4z + 5 = 0:
It is obviously parallel to PQ, since a normal is a line or vector that is perpendicular to a given object. The direction ratio simply states the number of units to move along each axis.
For any plane, ax + by + cz = d, where, a, b, and c are normal vectors to the plane.
Hence, the direction ratios are (a, b, c).
Therefore, the direction ratio of the normal = (2, -2, 4) for plane 2x - 2y + 4z + 5 = 0.
The Cartesian equation of the line PQ, where P(1, 3/2, 2) and Q (x₁ , y₁ , z₁) is:
$\frac{x_{1}-1}{2}=\frac{y_{1}-\frac{3}{2}}{-2}=\frac{z_{1}-2}{4}=\lambda(say)$
To find any point on this line,
$\frac{x_{1}-1}{2}=\lambda,\frac{y_{1}-\frac{3}{2}}{-2}=\lambda,\frac{z_{1}-2}{4}=\lambda$
$from \frac{x_{1}-1}{2}=\lambda\\\Rightarrow x_{1}-1=2\lambda\\\Rightarrow x_{1}=2\lambda+1\\ \\ \\ from \frac{y_{1}-\frac{3}{2}}{-2}=\lambda\\ \Rightarrow y_{1}-\frac{3}{2}=-2\lambda\\\Rightarrow y_{1}=\frac{3}{2}-2\lambda\\ \\ \\ from \frac{z_{1}-2}{4}=\lambda\\\Rightarrow z_{1}-2=4\lambda \\\Rightarrow z_{1}=4\lambda+2$
Any point on the line is $(2\lambda+ 1, \frac{3}{2} - 2\lambda, 4\lambda + 2).$
This point is Q.
$Q\left ( x_{1},y_{1},z_{1} \right )=Q(2\lambda+ 1, \frac{3}{2} - 2\lambda, 4\lambda + 2)....(i)$
And, it was assumed that is lies on the given plane. Substituting x₁, y₁, and z₁ in the plane equation, we get:
2x₁ - 2y₁ + 4z₁ + 5 = 0
$\Rightarrow 2\left (2\lambda+ 1 \right )-2\left ( \frac{3}{2} - 2\lambda \right )+4\left (4\lambda + 2 \right )+5=0$
Simplifying to find the value of $\lambda$
$\Rightarrow 4\lambda + 2 - 3 + 4\lambda + 16\lambda + 8 + 5 = 0\\ \Rightarrow 4\lambda + 4\lambda + 16\lambda + 2 - 3 + 8 + 5 = 0\\ \Rightarrow 24\lambda + 12 = 0\\ \Rightarrow 24\lambda = -12\\ \Rightarrow \lambda =-\frac{12}{24}\\ \Rightarrow \lambda =-\frac{1}{2}$
Since Q is the foot of the perpendicular from the point P,
We substitute the value of $\lambda$ in equation (i) to get:
$Q\left ( x_{1},y_{1},z_{1} \right )=Q(2(-\frac{1}{2})+ 1, \frac{3}{2} - 2(-\frac{1}{2}), 4(-\frac{1}{2}) + 2)\\ \Rightarrow Q\left ( x_{1},y_{1},z_{1} \right )=Q\left ( -1+1,\frac{3}{2}+1,-2+2 \right )\\ \Rightarrow Q\left ( x_{1},y_{1},z_{1} \right )=Q\left ( 0,\frac{5}{2},0 \right )$
Then, to find $\left | \vec{PQ} \right |$
Where, P = (1, 3/2, 2) and Q = (0, 5/2, 0)
$\left | \vec{PQ} \right |=\sqrt{\left (0-1 \right )^{2}+\left ( \frac{5}{2}-\frac{3}{2} \right )^{2}+\left ( 0-1 \right )^{2}}\\ \Rightarrow \left | \vec{PQ} \right |=\sqrt{(-1)^{2}+(1)^{2}+(-2)^{2}}\\ \Rightarrow \left | \vec{PQ} \right |=\sqrt{1+1+4}\\ \Rightarrow \left | \vec{PQ} \right |=\sqrt{6}$
Thus, the foot of the perpendicular from the given point to the plane is (0, 5/2, 0) and the distance is $\sqrt{6}$ units.

Question:19

Find the equations of the line passing through the point (3, 0, 1) and parallel to the planes x + 2y = 0 and 3y - z = 0.

Answer:

Given, a line passes through a point P (3, 0, 1) and is parallel to the planes x + 2y = 0 and 3y - z = 0.
We must find the equation of this line.
Let the position vector of point P be
$\vec{a}=3\hat{i}+0\hat{j}+\hat{k}$
Or,
$\vec{a}=3\hat{i}+\hat{k}.....(i)$
Let us consider the normal to the given planes, that is, perpendicular to the normal of the plane x + 2y = 0 and 3y - z = 0
Normal to the plane x + 2y = 0 can be given as $\vec{n_{1}}=\hat{i}+2\hat{j}$
Normal to the plane 3y - z = 0 can be given as $\vec{n_{2}}=3\hat{j}-\hat{k}$
So, $\vec{n}$ is perpendicular to both these normals.
So,
$\vec{n}=\vec{n_{1}}\times \vec{n_{2}}$
$\Rightarrow \vec{n}=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 2 & 0 \\ 0 & 3 & -1 \end{vmatrix}$
Taking the 1st row and the 1^st column, we multiply the 1^st element of the row $\left (a_{11} \right )$ with the difference of products of the opposite elements $\left (a_{22}\times a_{33}-a_{23} \times a_{32} \right )$ , excluding 1^st row and 1^st column
$\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33} \end{vmatrix}=a_{11}\left ( a_{22} \times a_{33}-a_{23} \times a_{32} \right )$
Here,
$\begin{vmatrix} \hat{i}& \hat{j} & \hat{j} \\ 1& 2 & 0 \\ 0& 3 & -1 \end{vmatrix}=\hat{i}\left ( \left ( 2 \times -1 \right )-\left (0 \times 3 \right ) \right )$
Now, we take the 2^nd column and 1^st row, and multiply the 2^nd element of the row (a??) with the difference of the product of opposite elements $\left (a_{21}\times a_{33}-a_{23} \times a_{31} \right )$
$\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33} \end{vmatrix}=a_{11}\left ( a_{22} \times a_{33}-a_{23} \times a_{32} \right )-a_{12}\left ( a_{21} \times a_{33}-a_{23} \times a_{31} \right )$
Here
$\begin{vmatrix} \hat{i}& \hat{j} & \hat{j} \\ 1& 2 & 0 \\ 0& 3 & -1 \end{vmatrix}=\hat{i}\left ( \left ( 2 \times -1 \right )-\left (0 \times 3 \right ) \right )-\hat{j}\left (\left ( 1 \times -1 \right )-\left ( 0 \times 0 \right ) \right )$
Finally, taking the 1^st row and 3^rd column , we multiply the 3^rd element of the row (a??) with the difference of the product of opposite elements $\left (a_{22}\times a_{33}-a_{23} \times a_{32} \right )$ excluding the 1^st row and 3^rd column.
$\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21}& a_{22} & a_{23} \\ a_{31}& a_{32} & a_{33} \end{vmatrix}=a_{11}\left ( a_{22} \times a_{33}-a_{23} \times a_{32} \right )-a_{12}\left ( a_{21} \times a_{33}-a_{23} \times a_{31} \right )+a_{13}\left ( a_{21} \times a_{32}-a_{22} \times a_{31} \right )$
Here
$\begin{vmatrix} \hat{i}& \hat{j} & \hat{j} \\ 1& 2 & 0 \\ 0& 3 & -1 \end{vmatrix}=\hat{i}\left ( \left ( 2 \times -1 \right )-\left (0 \times 3 \right ) \right )-\hat{j}\left (\left ( 1 \times -1 \right )-\left ( 0 \times 0 \right ) \right )+\hat{k}\left ( \left ( 1 \times 3 \right )-\left ( 2 \times 0 \right ) \right )$
Futher simplifying it,
$\Rightarrow \begin{vmatrix} \hat{i}& \hat{j} & \hat{j} \\ 1& 2 & 0 \\ 0& 3 & -1 \end{vmatrix}=\hat{i}\left ( -2-0 \right )-\hat{j}\left ( -1-0 \right )+\hat{k}\left ( 3-0 \right )\\ \\ \\ \Rightarrow \begin{vmatrix} \hat{i}& \hat{j} & \hat{j} \\ 1& 2 & 0 \\ 0& 3 & -1 \end{vmatrix}=-2\hat{i}+\hat{j}+3\hat{k}\\ \\ \\ \rightarrow \vec{n}=-2\hat{i}+\hat{j}+3\hat{k}$
Therefore, the direction ratio is (-2, 1, 3) …(iii)
We know, vector equation of any line passing through a point and parallel to a vector is $\vec{r}=\vec{a}+\lambda \vec{b}$ where $\lambda \epsilon \mathbb{R}$
Hence, from (i) and (ii),
$\vec{a}=3\hat{i}+\hat{k}\\ \vec{n}=-2\hat{i}+\hat{j}+3\hat{k}$

Putting these vectors in the equation $\hat{r}=\hat{a}+\lambda \hat{n}\\$

We get
$\hat{r}=\left ( 3\vec{i}+\vec{k} \right )+\lambda \left ( -2\hat{i}+\hat{j}+3\hat{k} \right )$
But we know,
$\hat{r}=x\vec{i}+y\hat{j}+z\vec{k}$
Substituting this,
$\left (x\vec{i}+y\hat{j}+z\vec{k} \right )=\left ( 3\hat{i}+\hat{k} \right )+\lambda\left ( -2\hat{i}+\hat{j}+3\hat{k} \right )\\ \\ \Rightarrow \left (x\vec{i}+y\hat{j}+z\vec{k} \right )-\left ( 3\hat{i}+\hat{k} \right )=\lambda\left ( -2\hat{i}+\hat{j}+3\hat{k} \right )\\ \\ \Rightarrow x\hat{i}+y\hat{j}+z\hat{k}-3\hat{i}-\hat{k}=\lambda \left ( -2\hat{i}+\hat{j}+3\hat{k} \right )\\ \\ \Rightarrow \left ( x-3 \right )\hat{i}+y\hat{j}+\left ( z-1 \right )\hat{k}=\lambda \left ( -2\hat{i}+\hat{j}+3\hat{k} \right )\\ \\$
Thus, the required equation of the line is $\left ( x-3 \right )\hat{i}+y\hat{j}+\left ( z-1 \right )\hat{k}=\lambda \left ( -2\hat{i}+\hat{j}+3\hat{k} \right )\\ \\$

Question:20

Find the equation of the plane through the points (2, 1, -1) and (-1, 3, 4) and perpendicular to the plane x - 2y + 4z = 10.

Answer:

Given, a plane passes through the points (2, 1, -1) and (-1, 3, 4) and is perpendicular to the plane x - 2y + 4z = 10.
We want to find the equation of this plane.
We know, the Cartesian equation of a plane passing through (x₁, y₁, z₁)
with direction ratios perpendicular to a, b, c for its normal is given as:
a (x - x₁) +b (y - y₁) + c (z - z₁) = 0
Hence,
Let us consider the equation of the plane passing through (2, 1, -1) to be
a(x – 2) + b(y – 1) + c(z – (-1)) = 0
⇒ a(x – 2) + b(y – 1) + c(z + 1) = 0 …(i)
Since it also passes through point (-1, 3, 4) we just replace x, y, z by -1, 3, and 4 respectively.
⇒ a(-1 – 2) + b(3 – 1) + c(4 + 1) = 0
⇒ -3a + 2b + 5c = 0 …(ii)
Since a, b, and c are direction ratios and this plane is perpendicular to the plane x - 2y + 4z = 10, we just replace x, y, and z with a, b, and c respectively (neglecting 10) and we equate this to 0.
=> a - 2b + 4c = 0 …(iii)
To solve two equations x₁a + y₁b + z₁c = 0 and x₂a + y₂b + z₂c = 0, we use the formula
$\frac{a}{\begin{vmatrix} y_{1} &z_{1} \\ y_{2}&z_{2} \end{vmatrix}}=\frac{b}{\begin{vmatrix} z_{1} &x_{1} \\ z_{2}&x_{2} \end{vmatrix}}=\frac{c}{\begin{vmatrix} x_{1} &y_{1} \\ x_{2}&y_{2} \end{vmatrix}}$
Similarly, to solve for equations (ii) and (iii):
$\frac{a}{\begin{vmatrix}2 &5 \\ -2&4 \end{vmatrix}}=\frac{b}{\begin{vmatrix} 5 &-3 \\ 4&1 \end{vmatrix}}=\frac{c}{\begin{vmatrix}-3 & 2 \\ 1&-2 \end{vmatrix}}$
$\Rightarrow \frac{a}{\left ( 2 \times 4 \right )-\left ( 5 \times -2 \right )}=\frac{b}{\left ( 5 \times 1 \right )-\left ( -3 \times 4 \right )}=\frac{c}{\left ( -3 \times -2 \right )-\left ( 2 \times 1 \right )}$
$\Rightarrow \frac{a}{8+10}=\frac{b}{5+12}=\frac{c}{6-2}$
$\Rightarrow \frac{a}{18}=\frac{b}{17}=\frac{c}{4}=\lambda$
$\Rightarrow \frac{a}{18}=\lambda, \frac{b}{17}=\lambda, \frac{c}{4}=\lambda$
That is,
$\Rightarrow \frac{a}{18}=\lambda\\ \Rightarrow a=18 \lambda\\ \\ \Rightarrow \frac{b}{17}=\lambda\\ \Rightarrow b=17 \lambda\\ \\ \Rightarrow \frac{c}{4}=\lambda\\ \Rightarrow c=4 \lambda\\ \\$
Substituting these values of a, b, and c in equation (i), we get
$a(x - 2) + b(y - 1) + c(z + 1) = 0\\ \Rightarrow 18\lambda(x - 2) + 17\lambda(y - 1) + 4\lambda(z + 1) = 0\\ \Rightarrow \lambda[18(x - 2) + 17(y - 1) + 4(z + 1)] = 0\\ \Rightarrow 18(x - 2) + 17(y - 1) + 4(z + 1) = 0\\ \Rightarrow 18x - 36 + 17y - 17 + 4z + 4 = 0\\ \Rightarrow 18x + 17y + 4z - 36 - 17 + 4 = 0\\ \Rightarrow 18x + 17y + 4z - 49 = 0\\ \Rightarrow 18x + 17y + 4z = 49\\$
Therefore, the required equation of the plane is 18x + 17y + 4z = 49.

Question:21

Find the shortest distance between the lines given by $r=\left ( 8+3\lambda \right )\hat{i}-\left ( 9+16\lambda \right )\hat{j}+\left ( 10+7\lambda \right )\hat{k}$ and $r=15\hat{i}+29\hat{j}+5\hat{k}+\mu\left ( 3\hat{i}+8\hat{j}-5\hat{k} \right )$

Answer:

Given two lines,
$\vec{r}=\left ( 8+3\lambda \right )\hat{i}-\left ( 9+16\lambda \right )\hat{j}+\left ( 10+7\lambda \right )\hat{k}...........(i)\\ \\ \vec{r}=15\hat{i}+29\hat{j}+5\hat{k}+\mu\left ( 3\hat{i}+8\hat{j}-5\hat{k} \right )...........(ii)$
Taking equation (i),
$\vec{r}=\left ( 8+3\lambda \right )\hat{i}-\left ( 9+16\lambda \right )\hat{j}+\left ( 10+7\lambda \right )\hat{k} \\ \Rightarrow \vec{r}= 8\hat{i}+3\lambda \hat{i}- 9\hat{j}+16\lambda \hat{j})+ 10 \hat{k}+7\lambda \hat{k} \\ \Rightarrow \vec{r}=8\hat{i}-9\hat{j}+10\hat{k}+3 \lambda \hat{i}-16 \lambda \hat{j}+7 \lambda \hat{k}\\ \Rightarrow \vec{r}=8\hat{i}-9\hat{j}+10\hat{k}+\lambda \left(3 \hat{i}-16 \hat{j}+7 \hat{k} \right ).............(iii)$
We know, the vector equation of a line passing through a point and parallel to a vector is where $\lambda\epsilon \mathbb{R}$
$\vec{a}$ = Position vector of the point through which line passes
$\vec{b}$ = Normal to the line
Comparing this with equation (iii), we get
$\vec{a_{1}}=8\hat{i}-9\hat{j}+10\hat{k}\\ \vec{b_{1}}=3\hat{i}-16\hat{j}+7\hat{k}\\$
Now take equation (ii)
$\vec{r}=15\hat{i}+29\hat{i}+5\hat{k}+\mu\left ( 3\hat{i}+8\hat{j}-5\hat{k} \right ) \\ \vec{r}=\left (15\hat{i}+29\hat{i}+5\hat{k} \right )+\mu\left ( 3\hat{i}+8\hat{j}-5\hat{k} \right )..........(iv)$
Similarly from (iv)
$\vec{a_{2}}=\left (15\hat{i}+29\hat{i}+5\hat{k} \right )\\ \vec{b_{2}}=\left ( 3\hat{i}+8\hat{j}-5\hat{k} \right )$
So, the shortest distance between two lines can be represented as:
$d=\left |\frac{\left ( \vec{b_{1}} \times \vec{b_{2}} \right ).\left ( \vec{a_{2}} - \vec{a_{1} }\right ) } {\left | \vec{b_{1}} \times \vec{b_{2}} \right |}\right |$
solve $\vec{b_{1}} \times \vec{b_{2}}$
$\vec{b_{1}} \times \vec{b_{2}}=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix}$
Taking 1^st row and 1^st column, we multiply the 1^st element of the row (a??) with the difference of the product of the opposite elements $\left ( a_{22}\times a_{33}-a_{23} \times a_{32}\right )$ , excluding the 1^st row and the 1^st column;
$\begin{vmatrix} a_{11} &a_{12} & a_{13} \\ a_{21} &a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}=a_{11}\left ( a_{22}\times a_{33}-a_{23} \times a_{32} \right )$
Here
$\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix}=\hat{i}\left (\left ( -16 \times -5 \right )-\left ( 7 \times 8 \right ) \right )$
Now, we take the 2nd column and 1st row, and multiply the 2nd element of the row (a??) with the difference of the product of opposite elements (a?? x a?? - a?? x a??)
$\begin{vmatrix} a_{11} &a_{12} & a_{13} \\ a_{21} &a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}=a_{11}\left ( a_{22}\times a_{33}-a_{23} \times a_{32} \right )-a_{12}\left ( a_{21}\times a_{33}-a_{23} \times a_{31} \right )$
Here
$\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix}=\hat{i}\left (\left ( -16 \times -5 \right )-\left ( 7 \times 8 \right ) \right )-\hat{j}\left (\left ( 3 \times -5 \right )-\left ( 7 \times 3 \right ) \right )$
Finally, taking the 1^st row and 3^rd column , we multiply the 3rd element of the row (a??) with the difference of the product of opposite elements (a?? x a?? - a?? x a??), excluding the 1^st row and 3^rd column.
$\begin{vmatrix} a_{11} &a_{12} & a_{13} \\ a_{21} &a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}=a_{11}\left ( a_{22}\times a_{33}-a_{23} \times a_{32} \right )-a_{12}\left ( a_{21}\times a_{33}-a_{23} \times a_{31} \right )+a_{13}\left ( a_{21}\times a_{32}-a_{22} \times a_{31} \right )$
Here
$\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix}=\hat{i}\left (\left ( -16 \times -5 \right )-\left ( 7 \times 8 \right ) \right )-\hat{j}\left (\left ( 3 \times -5 \right )-\left ( 7 \times 3 \right ) \right )+\hat{k}\left ( \left ( 3 \times 8 \right )-\left ( -16 \times 3 \right ) \right )$
Further simplifying it.
$\begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix}=\hat{i}\left (80-56 \right )-\hat{j}\left (-15-21 \right )+\hat{k}\left (24+48 \right )$
$\Rightarrow \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & -16 & 7 \\ 3 & 8 & -5 \end{vmatrix}=24\hat{i}+36\hat{j}+72\hat{k}\\ \\ \\ \Rightarrow \vec{b}\times \vec{b}= 24\hat{i}+36\hat{j}+72\hat{k}........(v)$
And,
$\left | \vec{b}\times \vec{b} \right |= \left |24\hat{i}+36\hat{j}+72\hat{k} \right |\\ \\ \Rightarrow \left | \vec{b}\times \vec{b} \right |=\sqrt{24^{2}+36^{2}+72^{2}} \\ \Rightarrow \left | \vec{b}\times \vec{b} \right |=12\sqrt{2^{2}+3^{2}+6^{2}} \\ \Rightarrow \left | \vec{b}\times \vec{b} \right |=12 \sqrt{4+9+36}\\ \Rightarrow \left | \vec{b}\times \vec{b} \right |=12\sqrt{49}\\ \Rightarrow \left | \vec{b}\times \vec{b} \right |=12 \times 7\\ \Rightarrow \left | \vec{b}\times \vec{b} \right |=84...........(vi)$
$Now \; \; solving \: \: \vec{a_{2}}- \vec{a_{1}}\\ \\ \vec{a_{2}}- \vec{a_{1}} =\left (15\hat{i}+29\hat{i}+5\hat{k} \right )-\left ( 8\hat{i}-9\hat{j}+10\hat{k} \right )\\ \Rightarrow \vec{a_{2}}- \vec{a_{1}} = 15\hat{i}-8\hat{i}+29\hat{j}+9\hat{j}+5\hat{k}-10\hat{k}\\ \Rightarrow \vec{a_{2}}- \vec{a_{1}} = 7\hat{i}+38\hat{j}-5\hat{k}.....(vii)$
Substituting the values from (v), (vi) and (vii) in d, we get
$d=\left |\frac{\left ( \vec{b_{1}} \times \vec{b_{2}} \right ).\left ( \vec{a_{2}} - \vec{a_{1} }\right ) } {\left | \vec{b_{1}} \times \vec{b_{2}} \right |}\right |$
$\Rightarrow d =\left | \frac{\left ( 24\hat{i}+36\hat{j}+72\hat{k} \right ).\left ( 7\hat{i}+38\hat{j}-5\hat{k} \right )}{84} \right |\\ \Rightarrow d =\left | \frac{24 \times 7 +36 \times 38+72 \times -5}{84} \right |\\ \Rightarrow d =\left | \frac{168+1368-360}{84} \right |\\ \Rightarrow d =\left | \frac{1176}{84} \right |\\ \Rightarrow d =14\\$
Thus, the shortest distance between the lines is 14 units.

Question:22

Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0 , which contains the line of intersection of the planes x + 2y + 3z - 4 = 0 and 2x + y -z + 5 = 0.

Answer:

Given, a plane is perpendicular to another plane 5x + 3y + 6z + 8 = 0,and also contains line of intersection of the planes x + 2y + 3z - 4 = 0 and 2x + y -z + 5 = 0.
We must find the equation of this plane.
We know, the equation of a plane passing through the line of intersection of the planes a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 is given as,
$( a_{1}x + b_{1}y + c_{1}z + d_{1}) +\lambda(a_{2}x + b_{2}y + c_{2}z + d_{2}) = 0$
Similarly, the equation of a plane through the line of intersection of the planes x + 2y + 3z - 4 = 0 and 2x + y -z + 5 = 0. is given by,
$(x + 2y + 3z - 4) + \lambda(2x + y - z + 5) = 0 \\ \Rightarrow x + 2y + 3z - 4 + 2\lambda x + \lambda - \lambda z + 5\lambda = 0\\ \Rightarrow x + 2 \lambda x + 2y + \lambda y + 3z - \lambda z - 4 + 5 \lambda = 0\\ \Rightarrow (1 + 2 \lambda)x + (2 + \lambda)y + (3 - \lambda)z - 4 + 5 \lambda = 0 ....(i)$
Thus, the direction ratio of plane in (i) is,
$(1 + 2\lambda, 2 + \lambda, 3 - \lambda)$
Since the plane in equation (i) is perpendicular to the plane 5x + 3y + 6z + 8 = 0;
we can replace x, y, z with (1 + 2λ), (2 + λ) and (3 - λ) respectively in the plane 5x + 3y + 6z + 8 = 0 (neglecting 8) and equating to 0.
This gives us,
$5(1 + 2\lambda) + 3(2 + \lambda) + 6(3 - \lambda) = 0\\ \Rightarrow 5 + 10\lambda + 6 + 3\lambda + 18 - 6\lambda = 0\\ \Rightarrow 10\lambda + 3\lambda- 6\lambda + 5 + 6 + 18 = 0\\ \Rightarrow 7\lambda + 29 = 0\\ \Rightarrow 7\lambda = -29\\ \Rightarrow \lambda=- \frac{29}{7}$
Substituting this value of $\lambda$ in equation (i) we get
$\left ( 1+2\left (-\frac{29}{7} \right ) \right )x+\left ( 2-\frac{29}{7} \right )y+\left ( 3+\frac{29}{7} \right )z-4+5\left (-\frac{29}{7} \right )=0\\ \\ \\ \Rightarrow \left ( 1+\frac{58}{7} \right )x+\left ( 2-\frac{29}{7} \right )y+\left ( 3+\frac{29}{7} \right )z-4-\frac{145}{7}=0\\ \\ \\ \Rightarrow \left ( \frac{7-58}{7} \right )x+\left ( \frac{14-29}{7} \right )y+\left ( \frac{21+29}{7} \right )z+\left ( \frac{-28-145}{7} \right )=0 \\ \\ \\ \Rightarrow -\frac{51}{7}x-\frac{15}{7}y+\frac{50}{7}z-\frac{173}{7}=0\\ \\ \\ \Rightarrow -51x - 15y + 50z - 173 = 0 \\ \\ \Rightarrow 51x + 15y - 50z + 173 = 0$
Thus, the required equation of the plane is 51x + 15y - 50z + 173 = 0.

Question:23

The plane ax + by = 0 is rotated about its line of intersection with the plane z = 0 through an angle α. Prove the equation of the plane in its new position is $ax+by\pm \left ( \sqrt{a^{2}+b^{2}} \tan \alpha \right )z=0$

Answer:

Given, the plane ax + by = 0 is rotated about its line of intersection with z = 0 by an angle $\alpha$
To prove: equation of the plane in its new position is
$ax+by\pm z\sqrt{a^{2}+b^{2}}\tan \alpha=0$
Proof: Two planes are given, ax + by = 0 …(i) and z = 0 …(ii)
We know, the equation of the plane passing through the line of intersection of the planes (i) and (ii) is
$ax + by + \lambda z = 0...(iii)$
where, $\lambda \epsilon \mathbb{R}$
The angle between the new plane and plane (i) is given as $\alpha$
Since the angle between two planes is equivalent to the angle between their normals, the direction ratio of normal to ax + by = 0 or ax + by +0z = 0 is (a, b, 0).
$\Rightarrow \vec{l}=a\hat{i}+b\hat{j}$
And, the direction ratio of normal to $ax + by + \lambda z = 0$ is (a, b, λ).
$\Rightarrow \vec{m}=a\hat{i}+b\hat{j}+\lambda \hat{k}$
Also, we know, angle between 2 normal vectors of the two given planes can be given as;
$\cos \alpha=\frac{\vec{l}\vec{m}}{\left |\vec{l} \right |\left |\vec{m} \right |}$
If we substitute the values of these vectors, we get
$\cos \alpha=\frac{\left (a\hat{i}+b\hat{j} \right )\left ( a\hat{i}+b\hat{j}+\lambda \hat{k} \right )}{\left |\left (a\hat{i}+b\hat{j} \right ) \right |\left |\left ( a\hat{i}+b\hat{j}+\lambda \hat{k} \right ) \right |}\\$
$\Rightarrow \cos \alpha=\frac{a.a+b.b+0.\lambda}{\sqrt{a^{2}+b^{2}}\sqrt{a^{2}+b^{2}+\lambda^{2}}}\\ \Rightarrow \cos \alpha=\frac{a^{2}+b^{2}}{\sqrt{a^{2}+b^{2}}\sqrt{a^{2}+b^{2}+\lambda^{2}}}$
We then multiply $\sqrt{a^{2}+b^{2}}$ by the numerator and denominator on the right hand side of the equation to get
$\Rightarrow \cos \alpha=\frac{a^{2}+b^{2}}{\sqrt{a^{2}+b^{2}}\sqrt{a^{2}+b^{2}+\lambda^{2}}}\times \frac{\sqrt{a^{2}+b^{2}}}{\sqrt{a^{2}+b^{2}}}\\ \\ \Rightarrow \cos \alpha=\frac{\left (a^{2}+b^{2} \right )\sqrt{a^{2}+b^{2}}}{\left (a^{2}+b^{2} \right )\sqrt{a^{2}+b^{2}+\lambda^{2}}}\\ \\ \Rightarrow \cos \alpha=\frac{\sqrt{a^{2}+b^{2}}}{\sqrt{a^{2}+b^{2}+\lambda^{2}}}\\ \\$
Applying square on both sides,
$\Rightarrow \cos^{2} \alpha=\left (\frac{\sqrt{a^{2}+b^{2}}}{\sqrt{a^{2}+b^{2}+\lambda^{2}}} \right )^{2}\\ \\ \Rightarrow \cos^{2} \alpha=\frac{a^{2}+b^{2}}{a^{2}+b^{2}+\lambda ^{2}}$
$\Rightarrow (a^{2} + b^{2} + \lambda^{2}) cos^{2} \alpha = a^{2} + b^{2}\\ \Rightarrow a^{2} \cos^{2} \alpha + b^{2} \cos^{2} \alpha + \lambda^{2} \cos^{2} \alpha = a^{2} + b^{2}\\ \Rightarrow \lambda^{2} \cos^{2} \alpha = a^{2} + b^{2} - a^{2} \cos^{2} \alpha -b^{2}\cos^{2} \alpha\\ \Rightarrow \lambda^{2} \cos^{2} \alpha = a^{2} - a^{2} \cos^{2} \alpha + b^{2} -b^{2} \cos^{2} \alpha\\ \Rightarrow \lambda^{2} \cos^{2} \alpha = a^{2}(1 -\cos^{2} \alpha) + b^{2}(1 - \cos^{2} \alpha)\\ \Rightarrow \lambda^{2} \cos^{2} \alpha = (a^{2} + b^{2})(1 - \cos^{2} \alpha)\\ \Rightarrow \lambda^{2} \cos^{2} \alpha = (a^{2} + b^{2}) \sin^{2} \alpha [since, \sin^{2} \alpha + \cos^{2} \alpha = 1]$
$\Rightarrow \lambda^{2} = \frac{(a^{2} + b^{2}) \sin^{2} \alpha }{\cos^{2} \alpha}\\ Since \frac{sin^{2}\alpha}{\cos^{2}\alpha}=\tan^{2}\alpha\\ \Rightarrow \lambda^{2}=\left ( a^{2}+b^{2} \right )tan^{2}\alpha\\ \Rightarrow \lambda =\pm \sqrt{\left ( a^{2}+b^{2} \right )tan^{2}\alpha}\\ \Rightarrow \lambda =\pm \sqrt{\left ( a^{2}+b^{2} \right )}tan^{2}\alpha\\$
Substituting the value of $\lambda$ in equation (iii) to find the plane equation,
ax + by + λz = 0
$\lambda =\pm \sqrt{\left ( a^{2}+b^{2} \right )}tan^{2}\alpha\\$
Hence proved.

Question:24

Find the equation of the plane through the intersection of the planes $r.\left ( \hat{i}+3\hat{j} \right )-6=0$ and $r.\left ( 3\hat{i}-\hat{j}-4\hat{k} \right )=0$ whose perpendicular distance from origin is unity.

Answer:

Given two planes,
$\vec{r}.\left ( \hat{i}+3\hat{j} \right )-6=0\\ \vec{r}.\left(3\hat{i}-\hat{j}-4\hat{k} \right )=0$
Also given, the perpendicular distance of the plane from the origin = 1.
We must find the equation of this plane.
We know,
$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}$
Simplifying the planes,
$\vec{r}.\left ( \hat{i}+3\hat{j} \right )-6=0\\ \Rightarrow \left ( x\hat{i}+y\hat{j}+z\hat{k} \right ).\left ( \hat{i}+3\hat{j} \right )-6=0\\ \Rightarrow x+3y-6=0........(i)$
Also, for
$\vec{r}.\left(3\hat{i}-\hat{j}-4\hat{k} \right )=0\\ \Rightarrow \left ( x\hat{i}+y\hat{j}+z\hat{k} \right ).\left(3\hat{i}-\hat{j}-4\hat{k} \right )=0\\ \Rightarrow 3x-y-4z=0$
The equation of a plane through the line of intersection of x + 3y - 6 = 0 and 3x - y - 4z = 0 can be given as
$(x + 3y - 6) + \lambda(3x - y - 4z) = 0\\ \Rightarrow x + 3y - 6 + 3\lambda x - \lambda y - 4\lambda z = 0\\ \Rightarrow x + 3\lambda x + 3y - \lambda y - 6 - 4\lambda z = 0\\ \Rightarrow (1 + 3\lambda)x + (3 - \lambda)y - 4\lambda z - 6 = 0 �(iii)$
Also, we know, the perpendicular distance of a plane, ax + by + cz + d = 0 from the origin, let’s say P, is given by
$P=\left | \frac{d}{\sqrt{a^{2}+b^{2}+c^{2}}} \right |$
Similarly, the perpendicular distance of the plane in equation (iii) from the origin (=1 according to the question) is:
$1=\left | \frac{-6}{\sqrt{\left ( 1+3 \lambda \right )^{2}+\left ( 3-\lambda \right )^{2}+\left ( -4\lambda \right )^{2}}} \right |\\ \\ \Rightarrow \sqrt{\left ( 1+3 \lambda \right )^{2}+\left ( 3-\lambda \right )^{2}+\left ( -4\lambda \right )^{2}}=6$
Taking the square of both sides,
$\Rightarrow \left (\sqrt{\left ( 1+3 \lambda \right )^{2}+\left ( 3-\lambda \right )^{2}+\left ( -4\lambda \right )^{2}} \right )^{2}=6^{2}$
$\Rightarrow (1 + 3\lambda)^{2} + (3 - \lambda)^{2} + (-4\lambda)^{2} = 36\\ \Rightarrow 1 + (3\lambda)^{2} + 2(1)(3\lambda) + (3)^{2} + \lambda^2 - 2(3)(\lambda) + 16\lambda^{2} = 36\\ \Rightarrow 1 + 9\lambda^{2} + 6\lambda + 9 + \lambda^{2} - 6\lambda + 16\lambda^{2} = 36\\ \Rightarrow 9\lambda^{2} + 16\lambda^{2} + \lambda^{2} + 6\lambda - 6\lambda = 36 - 1 - 9\\ \Rightarrow 26\lambda^{2} + 0 = 26\\ => \lambda^{2} = 26/26\\ => \lambda^{2} = 1\\ => \lambda = \pm 1$
First, we subsitute $\lambda=1$ in eq (iii) to find the plane equation
$(1 + 3\lambda)x + (3 - \lambda)y - 4\lambda z - 6 = `0\\ \Rightarrow (1 + 3(1))x - (3 - 1)y - 4(1)z - 6 = 0\\ \Rightarrow 4x - 2y - 4z- 6 = 0$
Now, we substitute λ= -1 in eq (iii) to find the plane equation
$(1 + 3\lambda)x + (3 - \lambda)y - 4 \lambda z - 6 = 0\\ \Rightarrow (1 + 3(-1))x + (3 - (-1))y - 4(-1)z - 6 = 0\\ \Rightarrow (1 - 3)x + (3 + 1)y + 4z - 6 = 0\\ \Rightarrow -2x + 4y + 4z - 6 = 0$
Therefore, the equation of the required plane is -2x + 4y + 4z – 6 = 0 and 4x – 2y – 4z – 6 = 0.

Question:25

Show that the points $\hat{i}-\hat{j}+3\hat{k}$ and $3\left ( \hat{i}+\hat{j}+\hat{k} \right )$ are equidistant from the plane $r.\left ( 5\hat{i}+2\hat{j}-7\hat{k} \right )+9=0$ and lies on the opposite of it.

Answer:

Given two points,
$\\\vec{A}=\hat{i}-\hat{j}+3\hat{k}\\ \vec{B}=3\left ( \hat{i}+\hat{j}+\hat{k} \right )=3\hat{i}+3\hat{j}+\hat{k}\\ \vec{r}.\left ( 5\hat{i}+2\hat{j}-7\hat{k} \right )+9=0$
Also,
$\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\\\\$
Where,
Therefore,
$\left (x\hat{i}+y\hat{j}+z\hat{k} \right ).\left (5\hat{i}+2\hat{j}-7\hat{k} \right )+9=0\\ \\ \Rightarrow 5x + 2y - 7z + 9 = 0$
We must show that the points A and B are equidistant from the plane
5x + 2y - 7z + 9 = 0
We also need to show that the points lie on the opposite side of the plane.
Normal of the plane is, $\vec{N=} 5{i} + 2\hat{j} - 7\hat{k}$
We know, the perpendicular distance of the position vector of a point
$\vec{A}=l \hat{i}+m \hat{j}+n \hat{k} \Rightarrow A(l,m,n)$ to the plane, p: ax + by + cz + d = 0 is given as: $D=\left | \frac{p(l,m,n)}{\left |\vec{N} \right |} \right |$
Where $\left |\vec{N} \right |=Normal \: vector\: of\: the\: plane$
$\vec{N} =a\vec{i}+b\vec{j}+c\vec{k}$
Thus, the perpendicular distance of the point $\vec{A} =\vec{i}-\vec{j}+3\vec{k}=A(1,-1,3)$ to the plane 5x + 2y - 7z + 9 = 0 having normal $\vec{N} =5\vec{i}+2\vec{j}-7\vec{k}$ is given by,
$\left | D_{1} \right |=\left |\frac{5(1)+2(-1)-7(3)+9}{|5\hat{i}+2\hat{j}-7\hat{k}|} \right |\\ \Rightarrow \left | D_{1} \right |=\left |\frac{5-2-21+9}{\sqrt{5^{2}+2^{2}+(-7)^{2}}} \right |\\ \Rightarrow \left | D_{1} \right |=\left |\frac{-9}{\sqrt{25+4+49}} \right |\\ \Rightarrow \left | D_{1} \right |=\left |\frac{9}{\sqrt{78}} \right |\\$
Hence, the perpendicular distance of the point $\vec{B}=3\hat{i}+3\hat{j}+3\hat{k}=B(3,3,3)$ to the plane 5x + 2y - 7z + 9 = 0 having normal $\vec{N}=5\hat{i}+2\hat{j}-7\hat{k}$
$\left | D_{2} \right |=\left |\frac{5(3)+2(3)-7(3)+9}{|5\hat{i}+2\hat{j}-7\hat{k}|} \right |\\ \Rightarrow \left | D_{2} \right |=\left |\frac{15+6-21+9}{\sqrt{5^{2}+2^{2}+(-7)^{2}}} \right |\\ \Rightarrow \left | D_{2} \right |=\left |\frac{9}{\sqrt{25+4+49}} \right |\\ \Rightarrow \left | D_{2} \right |=\left |\frac{9}{\sqrt{78}} \right |\\$
Therefore, |D₁| = |D₂|
However, D₁ and D₂ have different signs.
Therefore, the points A and B will lie on opposite sides of the plane.
Hence, we have successfully shown that the points are equidistant from the plane and lie on opposite sides of the plane.

Question:26

$AB=3\hat{i}-\hat{j}+\hat{k}\; \; and\; \; AB=-3\hat{i}+2\hat{j}+4\hat{k}$ are two vectors. The positions vectors of the points A and C are $6\hat{i}+7\hat{j}+4\hat{k}\; \; and\; \;-9\hat{j}+2\hat{k}$ respectively. Find the position vector of a point P on the line AB and a point Q on the line CD, such that PQ is perpendicular to AB and CD both.

Answer:

Given,
$\vec{AB}=3\hat{i}-\hat{j}+\hat{k}\\ \vec{CD}=-3\hat{i}+2\hat{j}+4\hat{k}$
And the position vectors
$\vec{OA}=6\hat{i}+7\hat{j}+4\hat{k}\\ \vec{OC}=-9\hat{j}+2\hat{k}$
Therefore, the line passing through A and along AB will have the equation:
$\vec{r}=6\hat{i}+7\hat{j}+4\hat{k}+\lambda\left ( 3\hat{i}-\hat{j}+\hat{k} \right )\\ \Rightarrow \vec{r}=\left ( 6+3\lambda \right )\hat{i}+\left ( 7-\lambda \right )\hat{j}+\left ( 4+\lambda \right )\hat{k}$
and the line passing through C and along CD will have equation
$\vec{r}=-9\hat{j}+2\hat{k}+\mu \left ( -3\hat{i}+2\hat{j}+4\hat{k} \right )\\ \Rightarrow \vec{r}=-3\mu \hat{i}+\left ( 2\mu-9 \right )\hat{j}+\left ( 2+4\mu \right )\hat{k}$
Now, PQ is a vector perpendicular to both AB and CD, such that Q lies on CD and P lies on AB. Thus, coordinates of P and Q will be of the form
$P (6 + 3\lambda, 7 - \lambda, 4 + \lambda)....(i)\\ Q (-3\mu, 2\mu - 9, 2 + 4\mu) .....(ii)$
Hence, the vector PQ will be given as
$\vec{PQ}=\left ( -3\mu-6-3\lambda \right )\hat{i}+\left ( 2\mu-16+\lambda \right )\hat{j}+\left ( 4\mu-2-\lambda \right )\hat{k}$
Now, since PQ is perpendicular to both, hence the dot products of AB.PQ and CD.PQ will be equal to 0.
AB. PQ = 0 and CD. PQ = 0
$AB. PQ = 3(-3\mu - 6 - 3\lambda) - (2\mu - 16 + \lambda) + (4\mu - 2 - \lambda)\\ \Rightarrow 0 = -9\mu - 18 - 9\lambda - 2\mu + 16 - \lambda + 4\mu - 2 - \lambda\\ \Rightarrow -7\mu - 11\lambda - 4 = 0.....(iii)\\ CD.PQ = 3(-3\mu - 6 - 3\lambda) + 2(2\mu - 16 + \lambda) + 4(4\mu - 2 - \lambda)\\ \Rightarrow 0 = -9\mu - 18 -9\lambda + 4\mu - 32 + 2\lambda +16 \mu -8 - 4\lambda\\ \Rightarrow 29\mu + 7\lambda - 22 = 0 ....(iv)$
Solving (iii) and (iv), we get
$\lambda = -1\; \; and \: \: \mu = 1$
Putting the value of $\lambda$ in (i) we get,
$P (6 + 3(-1), 7 - (-1), 4 + (-1))\\ P (6-3,7+1,4-1)\\ P (3,8,3)$
Putting the value of $\mu$ in (ii) we get,
$Q (-3(1), 2(1) - 9, 2 + 4(1))\\ Q (-3, 2 - 9, 2 +4)\\ Q (-3, -7, 6)$
Hence, position vector of P and Q will be
$\\\vec{OP}=3\hat{i}+8\hat{j}+3\hat{k}\\ \vec{OQ}=-3\hat{i}-7\hat{j}+6\hat{k}$

Question:27

Show that the straight lines whose direction cosines are given by 2l + 2m - n = 0 and mn + nl + lm = 0 are at right angles.

Answer:

We have given
$2l + 2m - n = 0...(i)\\ \Rightarrow n = 2(l + m)...(ii)$
, and
$mn + nl + lm = 0\\ \Rightarrow 2m(l + m) + 2(l + m)l + lm = 0\\ \Rightarrow 2lm + 2m^{2} + 2l^{2} + 2lm + lm = 0\\ \Rightarrow 2m^{2} + 5lm + 2l^{2} = 0\\ \Rightarrow 2m^{2} + 4lm + lm + 2l^{2} = 0\\ \Rightarrow (2m + l)(m + 2l) = 0$
Thus, we get two cases:
$l = -2m$
=> -4m + 2m - n = 0 [from (i)]
=> n = 2m
, and
m = -2l
=> 2l + 2(-2l) - n = 0
=> 2l - 4l = n
=> n = -2l
Hence, the direction ratios of one line is proportional to -2m, m or -2m or direction ratios are (-2, 1, -2) and the direction ratios of another line is proportional to l, -2l, -2l, or direction ratios are (1, -2, -2)
Thus, the direction vectors of two lines are $b_{1}=-2\hat{i}+\hat{j}-2\hat{k} \: and \: b_{2}=\hat{i}-2\hat{j}-2\hat{k}$
Also, the angle between the two lines $\vec{r}=\vec{a_{1}}+\lambda \vec{b_{1}} \: and \: \vec{r}=\vec{a_{2}}+\mu \vec{b_{2}}$ is given by:
$\cos \theta=\left |\frac{\vec{b_{1}}.\vec{b_{2}}}{\left |\vec{b_{1}} \right |\left |\vec{b_{2}} \right |} \right |$
Now,
$\vec{b_{1}}.\vec{b_{2}}=2(1)+1(-2)+(-2)(-2)\\ =2-2+4\\=0\\ \Rightarrow \cos\theta=0\\ \Rightarrow \theta=90^{\circ}$
Therefore, the lines have a 90⁰ angle between them.

Question:28

If l₁, m₁, n₁; l₂, m₂, n₂; l₃, m₃, n₃ are the direction cosines of 3 mutually perpendicular lines, prove that the line whose direction cosines are proportional to l₁ + l₂ + l₃ , m₁ + m₂ + m₃ , n₁ + n₂ + n₃ makes equal angles with them.

Answer:

Let the direction vector of the 3 mutually perpendicular lines be
$\vec{a}=l_{1}\hat{i}+m_{1}\hat{j}+n_{1}\hat{k}\\ \\ \vec{b}=l_{2}\hat{i}+m_{2}\hat{j}+n_{2}\hat{k}\\ \\ \vec{c}=l_{3}\hat{i}+m_{3}\hat{j}+n_{3}\hat{k}$
Let the direction vectors associated with direction cosines $l_{1} + l_{2} + l_{3} , m_{1} + m_{2} + m_{3} , n_{1} + n_{2} + n_{3}$ be
$\vec{p}=\left (l_{1} + l_{2} + l_{3} \right )\hat{i}+\left (m_{1} + m_{2} + m_{3} \right )\hat{j}+\left ( n_{1} + n_{2} + n_{3} \right )\hat{k}$
Since the lines associated with the direction vectors a, b, and c are mutually perpendicular, we get
$\vec{a}.\vec{b}=0$ (Since the dot product of two perpendicular vectors is 0)
=> $l_{1}l_{2} + m_{1}m_{2}+n_{1}n_{2}=0$ …(1)
Similarly,
$l_{1}l_{3} + m_{1}m_{3}+n_{1}n_{3}=0$ …(2)
Finally, $\vec{b}.\vec{c}=0$
=> $l_{2}l_{3} + m_{2}m_{3}+n_{2}n_{3}=0$ …(3)
Now, let us consider x, y and z as the angles made by direction vectors a, b, and c respectively with p.
Then,
$\cos x=\vec{a}.\vec{p}$
$\Rightarrow \cos x =l_{1}\left ( l_{1}+l_{2}+l_{3} \right )+m_{1}\left ( m_{1}+m_{2}+m_{3} \right )+n_{1}\left ( n_{1}+n_{2}+n_{3} \right )\\ \Rightarrow \cos x=l_{1}^{2}+l_{1}l_{2}+l_{1}l_{3}+m_{1}^{2}+m_{1}m_{2}+m_{1}m_{3}+n_{1}^{2}+n_{1}n_{2}+n_{1}n_{3}\\ \Rightarrow cos x= l_{1}^{2}+m_{1}^{2}+n_{1}^{2}+\left ( l_{1}l_{2}+m_{1}m_{2}+ n_{1}n_{2} \right )+\left ( l_{1}l_{3}+m_{1}m_{3}+ n_{1}n_{3} \right )\\$
We know, $l_{1}^{2}+m_{1}^{2}+n_{1}^{2}=1$ [since the sum of squares of direction cosines of a line = 1]
$\Rightarrow \cos x=1+0=1$ [from (1) and (2)]
Then, $\cos y=1$ and $\cos z=1$
=> x = y = z = 0.
Therefore, the vector p makes equal angles with the vectors a, b and c.

Question:29

Distance of the point (α, β, y) is:
A. β B. |β| C. |β| + |y| D. √(α² + y²)

Answer:

Drawing a perpendicular from (α, β, y) to the y-axis gives us a foot of $\left ( \alpha ,\beta ,\gamma \right )$ perpendicular with coordinates (0, β, 0).
Also, using the distance formula, we can calculate the distance between two points as:
$AB=\sqrt{\left ( x_{2}-x_{1} \right )^{2}+\left ( y_{2}-y_{1} \right )^{2}+\left ( z_{2}-z_{1} \right )^{2}}$
Thus, the required distance $=\sqrt{\left ( \alpha-0 \right )^{2}+\left ( \beta-\beta \right )^{2}+\left(\gamma-0 \right )^{2}}=\sqrt{\alpha^{2}+\gamma^{2}}$
(Option D)

Question:30

If the direction cosines of a line are k, k, k, then:
A. k > 0
B. 0 < k < 1
C. k = 1
D. k = 1/√3 or -1/√3

Answer:

We know that the sum of squares of the direction cosines of a line = 1
=> k² + k² + k² = 1
=> 3k² = 1
$\Rightarrow k=\pm\frac{1}{\sqrt{3}}$ (Option D)

Question:31

The distance of the plane $\vec{r}.\left ( \frac{2}{7}\hat{i}+\frac{3}{7}\hat{j}-\frac{6}{7}\hat{k} \right )=1$ from the origin is:
A. 1
B. 7
C. 1/7
D. None of these

Answer:

Given plane is
$\vec{r}.\left ( \frac{2}{7}\hat{i}+\frac{3}{7}\hat{j}-\frac{6}{7}\hat{k} \right )=1$
Let
$\vec{n}=\frac{2}{7}\hat{i}+\frac{3}{7}\hat{j}-\frac{6}{7}\hat{k}$
$\left |\vec{n} \right |=\sqrt{\frac{2}{7}\hat{i}+\frac{3}{7}\hat{j}-\frac{6}{7}\hat{k} }=1$
=> n is a unit vector
Thus, the equation of the plane is of the form $\vec{r}.\hat{n} =d$ , where n is
the unit vector and d is the distance from the origin.
Comparing, we get d =1, hence the distance of the plane from origin is 1
(Option A)

Question:32

The sine of the angle between the straight line $\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}$ and
The plane 2x - 2y + z = 5 is:
A. 10/6√5
B. 4/5√2
C. 2√3/5
D. √2/10

Answer:

The equation of the line is given as
$\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}$
The direction vector of this line can be represented as $\vec{b}=3\hat{i}+4 \hat{j}+5\hat{k}$
Also given is the equation of the plane 2x - 2y + z = 5
The normal to this plane is, $\vec{n}=2\hat{i}-2 \hat{j}+\hat{k}$
We also know that the angle $\phi$ between the line with the direction
vector b and the plane with the normal vector n is,
$\sin \phi =\left | \frac{\vec{b}.\vec{n}}{\left | \vec{b} \right |\left | \vec{n} \right |} \right |$
$\Rightarrow \sin \phi =\left |\frac{3(2)+4(-2)+5(1)}{\sqrt{3^{2}+4^{2}+5^{2}}\sqrt{2^{2}+(-2)^{2}+1^{2}}} \right |$
$\Rightarrow \sin \phi =\left |\frac{3}{3\sqrt{50}} \right |$
$=\frac{1}{5\sqrt{2}}\times \frac{\sqrt{2}}{\sqrt{2}}$
$=\frac{\sqrt{2}}{10}$
(Option D)

Question:33

The reflection of the point (α, β, γ) in the xy- plane is:
A. (α, β, 0)
B. (0, 0, γ)
C. (-α, -β, -γ)
D. (α, β, -γ)

Answer:

a33
The equation of the XY plane is Z = 0
Given point (α, β, γ); if we draw a perpendicular from this point in the XY plane, the coordinates of the plane will be
(α, β, 0).
Let the reflection be (x, y, z)
So, $\alpha=\frac{\alpha+x}{2}$
=> x = α
$\beta=\frac{\beta+y}{2}$
=> y = β
$0=\frac{\gamma+z}{2}$
=> z = -γ
The reflection is: (α, β, -γ). (option D)

Question:34

The area of the quadrilateral ABCD, where A (0, 4, 1), B (2, 3, -1), C (4, 5, 0) and D (2, 6, 2) is equal to:
A. 9 square units
B. 18 square units
C. 27 square units
D. 81 square units

Answer:

Given, A (0, 4, 1), B (2, 3, -1), C (4, 5, 0) and D (2, 6, 2);
$\vec{AB}=\left ( 2-0 \right )\hat{i}+\left ( 3-4 \right )\hat{j}+\left ( -1-1 \right )\hat{k}=2\hat{i}-\hat{j}-2\hat{k}$
$\vec{BC}=\left ( 4-2\right )\hat{i}+\left ( 5-3 \right )\hat{j}+\left ( 0-(-1) \right )\hat{k}=2\hat{i}+2\hat{j}+\hat{k}$
$\vec{CD}=\left ( 2-4\right )\hat{i}+\left ( 6-5 \right )\hat{j}+\left ( 2-0 \right )\hat{k}=-2\hat{i}+\hat{j}+2\hat{k}=-\vec{AB}$
$\vec{DA}=\left ( 0-2\right )\hat{i}+\left ( 4-6 \right )\hat{j}+\left ( 1-2 \right )\hat{k}=-2\hat{i}-2\hat{j}-1\hat{k}=-\vec{BC}$
Since opposite vectors of this parallelogram are equal and opposite, ABCD is a parallelogram and we know the area of a parallelogram is | AB x CD|
$=\begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ 2 & -1 & -2 \\ 2 & 2 & 1 \end{vmatrix}$
$=\left | \hat{i}\left ( -1+4 \right )+\hat{j}\left ( -4-2 \right )+\hat{k}\left ( 4+2 \right ) \right |$
$=\left | 3\hat{i}-6\hat{j}+6\hat{k} \right |$
$=\sqrt{3^{2}+(-6)^{2}+6^{2}}=\sqrt{81}$
= 9 square units (Option A).

Question:35

The locus represented by xy + yz = 0 is:
A. A pair of perpendicular lines
B. A pair of parallel lines
C. A pair of parallel planes
D. A pair of perpendicular planes

Answer:

Given, xy + yz = 0
=> x (y + z) = 0
=> x = 0 and y + z = 0
Clearly, the above equations are the equations of planes [of the form ax + by + cz + d = 0]
Also, x = 0 has the normal vector $\hat{i}$
And y + z = 0 has the normal vector $\hat{j}+\hat{k}$
And the dot product of these two is
$\hat{i}\left (\hat{j}+\hat{k} \right )=\hat{i}.\hat{j}+\hat{i}.\hat{k}$
= 0
Hence, the planes are perpendicular (Option D).

Question:36

The plane 2x - 3y + 6z - 11 = 0 makes an angle $\sin^{-1}(\alpha)$ with the x-axis. The value of α is:
A. $\frac{\sqrt{3}}{2}$
B. $\frac{\sqrt{2}}{3}$
C. $\frac{2}{7}$
D. $\frac{3}{7}$

Answer:

Given, the equation of the plane is 2x - 3y + 6z - 11 = 0.
The normal to this plane is,
$\vec{n}=2\hat{i}-3\hat{j}+6\hat{k}$
Also, the x-axis has the direction vector $\vec{b}=\hat{i}$
Also, we know that the angle $\varphi$ between the line with direction vector b and the plane having the normal vector n is:
$\\ \sin \varphi =\left | \frac{\vec{b}.\vec{n}}{\left |\vec{b} \right |.\left |\vec{n} \right |} \right |\\ \Rightarrow \sin \varphi=\left | \frac{1(2)+0(-3)+0(6)}{\sqrt{2^{2}+3^{2}+6^{2}}\sqrt{1^{2}+0^{2}+0^{2}}} \right |\\ \Rightarrow \sin \varphi = \left | \frac{2}{\sqrt{49}} \right |=\frac{2}{7}\\\Rightarrow \varphi =\sin^{-1}\left ( \frac{2}{7} \right )$
On comparing, we find $\alpha =\frac{2}{7}$ (Option C)

Question:37

Fill in the blanks:
A plane passes through the points (2, 0, 0), (0, 3, 0) and (0, 0, 4). The equation of the plane is ______.

Answer:

We know, the equation of a plane cutting the coordinate axes at (a, 0, 0), (0, b, 0) and (0, 0, c) is given as
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$
In this case, a = 2, b = 3, and c = 4.
Therefore, putting these values in the equation of the plane, we get
$\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1$

Question:38

Fill in the blanks: The direction cosines of the vector $\left ( 2\hat{i}+2\hat{j}-\hat{k} \right )$ are _______.

Answer:

If l, m, and n are the direction cosines and the direction ratios of a line are a, b, and c, then we know:
$\\l=\frac{a}{\sqrt{a^{2}+b^{2}+c^{2}}} \\m=\frac{b}{\sqrt{a^{2}+b^{2}+c^{2}}}\\l=\frac{c}{\sqrt{a^{2}+b^{2}+c^{2}}}$
According to the question,
a = 2, b = 2, c = -1
Then
$\sqrt{a^{2}+b^{2}+c^{2}}=\sqrt{2^{2}+2^{2}+(-1)^{2}}=3$
Thus, the direction cosines are
l = 2/3, b = 2/3, c = -1/3

Question:39

Fill in the blanks: The vector equation of the line $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$ is __________.

Answer:

The equation of the line is given as
$\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$
Clearly, the line passes through A (5, -4, 6) and has the direction ratios 3, 7, and 2.
Also, the position vector of A is $\vec{a}=5\hat{i}-4\hat{j}+6\hat{k}$
The direction vector of the given line will be:
$\vec{b}=3\hat{i}+7\hat{j}+2\hat{k}$
Also, the vector equation of a line passing through the given point whose position vector is a and b is:
$\vec{r}=\vec{a}+\lambda \vec{b}$
Hence, the required equation of the line will be:
$\vec{r}=\left ( 5\hat{i}-4\hat{j}+6\hat{k} \right )+\lambda\left ( 3\hat{i}+7\hat{j}+2\hat{k}\right )$

Question:40

Fill in the blanks: The Cartesian equation $\vec{r}.\left ( \hat{i}+\hat{j}-\hat{k} \right )=2$ of the plane is ______.

Answer:

By expanding the dot product given in the question, we can get the Cartesian equation of the plane.
Given: $\vec{r}.\left ( \hat{i}+\hat{j}-\hat{k} \right )=2$
$\vec{r}=x\hat{i}+y\hat{j}-z\hat{k}$
Putting
$\Rightarrow \left ( x\hat{i}+y\hat{j}+z\hat{k} \right )\left ( \hat{i}+\hat{j}-\hat{k} \right )=2$
$\Rightarrow x + y - z = 2$
Thus, the required Cartesian equation is x + y - z = 2.

Question:41

State True or False for the given statement:
The unit vector normal to the plane $x + 2y +3z - 6 = 0$ is $\frac{1}{\sqrt{14}}\hat{i}+\frac{2}{\sqrt{14}}\hat{j}+\frac{3}{\sqrt{14}}\hat{k}$

Answer:

Given, the equation of the plane is x + 2y + 3z - 6 = 0
The normal to this plane will be 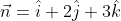$\vec{n}=\hat{i}+2\hat{j}+3\hat{k}$ The unit vector of this normal is:
$\\ \vec{n}=\frac{\vec{n}}{\left |\vec{n} \right |}\\ \vec{n}=\frac{\hat{i}+2\hat{j}+3\hat{k}}{\sqrt{1^{2}+2^{2}+3^{2}}}=\frac{1}{\sqrt{14}}\hat{i}+\frac{2}{\sqrt{14}}\hat{j}+\frac{3}{\sqrt{14}}\hat{k}$
Therefore, the statement is True

Question:42

Fill in the blanks:
The vector equation of the line that passes through the points (3, 4, -7) and (1, -1, 6) is ______.

Answer:

The position vector of the first point (3, 4, -7) is $\vec{a}=3\hat{i}+4\hat{j}-7\hat{k}$
And the position vector of the second point(1, -1, 6): $\vec{b}=\hat{i}-\hat{j}+6\hat{k}$

Also, the vector equation of a line passing through two points with position vectors a and b is given by:
$\vec{r}=\vec{a}+\lambda\left ( \vec{b}-\vec{a} \right )$
Thus, the required line equation is
$\vec{r}=3\hat{i}+4\hat{j}-7\hat{k}+\lambda\left ( \hat{i}-\hat{j}+6\hat{k}-\left ( 3\hat{i}+4\hat{j}-7\hat{k} \right ) \right )$
$\vec{r}=3\hat{i}+4\hat{j}-7\hat{k}+\lambda\left ( -2\hat{i}-5\hat{j}+13\hat{k} \right )$

Question:43

State True or False for the given statement:
The intercepts made by the plane $2x - 3y + 5z + 4 = 0$ on the coordinate axes are $-2, \frac{4}{3},\frac{-4}{5}$

Answer:

To begin with, we convert the given plane equation to intercept form:
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$ where a, b, and c are the intercepts on x, y, and z, axes respectively.
Given, $2x - 3y + 5z + 4 = 0$
$\Rightarrow -2x + 3y - 5z = 4$
Dividing this equation on both sides by 4,
$\Rightarrow \frac{-1}{2}x + \frac{3}{4}y - \frac{5}{4}z = 1$
On comparison, we get the intercepts -2, 4/3, and -4/5 respectively.
Therefore, the statement is True.

Question:44

State True or False for the given statement: The angle between the line $r=\left ( 5 \hat{i}-\hat{j}-4\hat{k} \right )+\lambda\left ( 2 \hat{i}-\hat{j}+k \right )$ and the plane $r.\left ( 3 \hat{i}-4\hat{j}-\hat{k} \right )+5=0\, \, \, \, \, \, \sin^{-1}\frac{5}{2\sqrt{91}}$ is

Answer:

We know, the angle $\phi$ between the plane with normal vector n and the line with direction vector b is denoted by:
$\sin\varphi\frac{\vec{b}.\vec{n}}{\left |\vec{b} \right |.\left |\vec{n} \right |}$
Given equation of the line is $r=\left ( 5 \hat{i}-\hat{j}-4\hat{k} \right )+\lambda\left ( 2 \hat{i}-\hat{j}+k \right )$
Hence, its direction vector will be:
$\vec{b}=2\hat{i}-\hat{j}+\hat{k}$
Given equation of the plane is $\vec{r}.\left (3\hat{i}-4\hat{j}-\hat{k} \right )+5=0$
Hence, its normal vector will be:
$\vec{n}=3\hat{i}-4\hat{j}-\hat{k}$
Thus, we have:
$\sin\varphi =\left | \frac{\left ( 2\hat{i}-\hat{j}+\hat{k} \right )\left ( 3\hat{i}-4\hat{j}-\hat{k} \right )}{\sqrt{2^{2}+(-1)^{2}+1^{2}}\sqrt{3^{2}+(-4)^{2}+(-1)^{2}}} \right |\\ \Rightarrow \sin \varphi=\frac{2(3)-1(-4)+1(-1)}{\sqrt{6}\sqrt{26}}=\frac{9}{\sqrt{156}}=\frac{9}{2\sqrt{39}}$
$\varphi =\sin^{-1}\frac{9}{2\sqrt{39}}$
Therefore, the given statement is False.

Question:45

State True or False for the given statement:
The angle between the planes $r.\left ( 2\hat{i}-3\hat{j}+\hat{k} \right )=1$ and $\bar{r}.\left ( \hat{i}-\hat{j} \right )=4$ is $\cos^{-1}\frac{-5}{\sqrt{58}}$

Answer:

In vector form, if we take θ as the angle between the two planes
$\vec{r}.\vec{n_{1}}=\vec{d_{1}}$ and $\vec{r}.\vec{n_{2}}=\vec{d_{2}}$
Then
$\theta=\frac{\left | \vec{n_{1}}.\vec{n_{2}} \right |}{\left | \vec{n_{1}} \right |\left | \vec{n_{2}} \right |}$
Now, the given planes are $\vec{r}.\left ( 2\hat{i}-3\hat{j}+\hat{k} \right )=1$ and $\vec{r}.\left ( \hat{i}-\hat{j}\right )=4$

Here, $\vec{n_{1}}=2 \hat{i}-3\hat{j}+\hat{k}$ and $\vec{n_{2}}=\hat{i}-\hat{j}$
Therefore,
$\theta =\cos^{-1}\frac{2(1)+3(1)+1(0)}{\sqrt{2^{2}+(-3)^{2}+1^{2}}\sqrt{1^{2}+(-1)^{2}+0^{2}}}$
$=\cos^{-1}\frac{5}{\sqrt{2}\sqrt{14}}\\=\cos^{-1}\frac{5}{2\sqrt{7}}$
The statement is False.

Question:46

State True or False for the given statement:
The line $r=2\hat{i}-3\hat{j}-\hat{k}+\lambda\left ( \hat{i}-\hat{j}+2\hat{k} \right )$ lies in the plane $r.\left (3\hat{i}+\hat{j}-\hat{k} \right )+2=0$

Answer:

The equation of the line is given as
$\Rightarrow \vec{r}=2\hat{i}-3\hat{j}-\hat{k}+\lambda \left ( \hat{i}-\hat{j}+2\hat{k} \right )\\ \Rightarrow \vec{r}=\left ( 2+\lambda \right )\hat{i}+\left ( -3-\lambda \right )\hat{j}+\left ( -1+2\lambda \right )\hat{k}$
Any point lying on this line will satisfy the plane equation if the line itself lies in the plane. Also, any point on this line will have a position vector:
$\vec{a}=\left ( 2+\lambda \right )\hat{i}+\left ( -3-\lambda \right )\hat{j}+\left ( -1+2\lambda \right )\hat{k}$
Given equation of the plane $\vec{r}.\left ( 3\hat{i}+\hat{j}-\hat{k} \right )+2=0$
If we put a in the above equation,
$\left (\left (2 + \lambda \right )\hat{i}+ \left(-3 - \lambda \right) \hat{j} + \left (-1 + 2\lambda \right)\hat{k} \right ).\left ( 3\hat{i}+\hat{j}-\hat{k} \right ) + 2 \\ = \left (2 + \lambda \right ) \left(3\right) + \left(-3 - \lambda \right) \left(1\right) + \left (-1 + 2\lambda \right)\left(-1 \right) + 2 \\ = 6 - 3\lambda - 3 - \lambda + 1 - 2\lambda + 2 \\ = 5 - 6\lambda \neq R.H.S$
Thus, the line does not lie in the given plane.
Therefore, the given statement is False.

Question:47

State True or False for the given statement.
The vector equation of the line $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$ is $r=5\hat{i}-4\hat{j}+6\hat{k}+\lambda\left ( 3\hat{i}+7\hat{j}+2\hat{k} \right )$

Answer:

The given equation of the line is $\frac{x-5}{3}=\frac{y+4}{7}=\frac{z-6}{2}$
It is clear from the equation that this line passes through A (5, -4, 6) and has the direction ratios 3, 7 and 2.
The position vector of A is $\vec{a}=5\hat{i}-4\hat{j}+6\hat{k}$
And the direction vector of the line will be
We know, the vector equation of a line that passes through a given point with position vector a and b is given as
$\vec{r}=3\hat{i}+7\hat{j}+2\hat{k}$
Hence, the required line equation will be:
$\hat{r}=\left ( 5\hat{i}-4\hat{j}+6\hat{k}\right )\lambda\left ( 3\hat{i}+7\hat{j}+2\hat{k} \right )$
Thus, the statement is True.

Question:48

State True and False for the given statement:
The equation of a line, which is parallel to $2 \hat{i}+\hat{j}+3\hat{k}$ and which passes through (5, -2, 4) is $\frac{x-5}{2}=\frac{y+2}{-1}=\frac{z-4}{3}$

Answer:

We know, the equation of a line in Cartesian form is
$\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}$
, where a, b and c are the direction ratios and (x₁, y₁, z₁) is a particular point on the line.
The given line is parallel to therefore it has 2, 1, 3 as direction ratios.
(a = 2, b = 1, c = 3)
The line passes through (5, -2, 4)
Substituting these values, we get the equation of line:
$\frac{x-5}{2}=\frac{y+2}{1}=\frac{z-4}{3}$
Thus, the given statement is False.

Question:49

State True or False for the given statement:
If the foot of the perpendicular drawn from the origin to a plane is (5, -3, -2) then the equation of the plane is $r.\left ( 5\hat{i}-3\hat{j}-2\hat{k} \right )=38$

Answer:

a49
Let us take O as the origin, P as the foot of the perpendicular drawn from origin to the plane.
Then the position vector OP is:
$\vec{n}=\vec{OP}=5\hat{i}-3\hat{j}-2\hat{k}$
The unit vector of n is:
$\vec{n}=\frac{\vec{n}}{\left | \vec{n} \right |}\\ \hat{n}=\frac{5\hat{i}-3\hat{j}-2\hat{k}}{\sqrt{5^{2}+(-3)^{2}+(-2)^{2}}}=\frac{5}{\sqrt{38}}\hat{i}-\frac{3}{\sqrt{38}}\hat{j}-\frac{2}{\sqrt{4}}\hat{k}$
$OP =\sqrt{\left ( 5-0 \right )^{2}+\left ( -3-0 \right )^{2}+\left (-2-0 \right )^{2}} \\ =\sqrt{25+9+4}\\ =\sqrt{38}$
Now, the equation of the plane with unit normal vector n and having a perpendicular drawn from the origin d is:
$\vec{r}.\hat{n}=d$
Therefore,
Equation of the given plane will be,
$\vec{r}.\left ( \frac{5}{\sqrt{38}}\hat{i}-\frac{3}{\sqrt{38}}\hat{j}-\frac{2}{\sqrt{4}}\hat{k} \right )=\sqrt{38}\\ \Rightarrow \vec{r}.\left ( 5\hat{i}-3\hat{j}-2\hat{k} \right )=38$
=> The given statement is True.

Main Subtopics of NCERT Exemplar Class 12 Maths Solutions Chapter 11

The main topics and sub topics covered in this chapter of are as follows:

Direction aspects of a line
Direction Cosines
Direction Ratios
Relation between the direction cosines of a line
Direction Cosines of a line passing through two points
Equation of a line in space
Equation of a line through a given point and parallel to a given vector
Equation of a line passing through two given points
Derivation of Cartesian form from Vector form.
Angle between two lines
Shortest distance between two lines
Distance between two skew lines
Distance between parallel lines
Planes
Equation of a plane in Normal form
Equation of a plane perpendicular to a given vector through a given point
Equation of a plane passing through three non-collinear points
Planes passing through the intersection of two given planes
Coplanarity of two lines
Angle between two planes
Distance of a point from a plane
Angle between a line and a plane

What will the students learn in NCERT Exemplar Class 12 Maths Solutions Chapter 11?

NCERT exemplar Class 12 Maths solutions chapter 11 would not only help you find volumes of objects such as cubes, cylinders, pyramids, or location of coordinates but also to expand your learning and potential to achieve academic excellence.
The design of assembly systems in manufacturing automobiles and nanotechnology is done with 3D geometry. Various graphic designers, visual artists, and game developers use the concepts of three dimensions to create computer graphics, visual graphs, virtual reality programs, and video games.
Geometry acts as a fundamental tool to calculate the location of interplanetary and galactic objects in space and to draft a possible trajectory and find out the entry points to a planet’s atmosphere for a space vehicle's journey.
Thus, NCERT exemplar solutions for Class 12 Maths chapter 11 exposes one to a wide array of fields like art, technology, architecture, astronomy and physics, and aspects of geographic information systems.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

NCERT Exemplar Class 12 Maths Solutions

Chapter 1 Relations and Functions

Chapter 2 Inverse Trigonometric Functions

Chapter 3 Matrices

Chapter 4 Determinants

Chapter 5 Continuity and Differentiability

Chapter 6 Applications of Derivatives

Chapter 7 Integrals

Chapter 8 Applications of Integrals

Chapter 9 Differential Equations

Chapter 10 Vector Algebra

Chapter 12 Linear Programming

Chapter 13 Probability

Importance of NCERT Exemplar Class 12 Maths Solutions Chapter 11

· NCERT Exemplar Class 12 Maths chapter 11 solutions define Dimension as the standard measure of an object's size and shape.

· We would use the concept of Vector algebra to make three-dimensional geometry organised and straightforward.

· In Class 12 Maths NCERT exemplar solutions chapter 11, we will study the direction aspects of a line joining two points, including the direction cosines and the ratios, discuss the equations of lines and planes in space, measure the shortest distance between two lines and learn more about the Cartesian form analytical and geometric representation.

NCERT Exemplar Class 12 Solutions

NCERT Exemplar Class 12 Chemistry Solutions

NCERT Exemplar Class 12 Physics Solutions

NCERT Exemplar Class 12 Biology Solutions

Also, check NCERT Solutions for questions given in the book:

Chapter 1	Relations and Functions
Chapter 2	Inverse Trigonometric Functions
Chapter 3	Matrices
Chapter 4	Determinants
Chapter 5	Continuity and Differentiability
Chapter 6	Application of Derivatives
Chapter 7	Integrals
Chapter 8	Application of Integrals
Chapter 9	Differential Equations
Chapter 10	Vector Algebra
Chapter 11	Three Dimensional Geometry
Chapter 12	Linear Programming
Chapter 13	Probability

Must Read NCERT Solution subject wise

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Also Check NCERT Books and NCERT Syllabus here

Frequently Asked Questions (FAQs)

1. What are the topics covered in this chapter?

This entire chapter talks about the dimensional geometry which covered vector usage to measure and determine line, planes and angles.

2. Are these solutions helpful in board exams?

Yes, for those who want a clear picture of how to solve questions in three-dimensional geometry, our NCERT exemplar Class 12 Maths solutions chapter 11 can be highly supportive.

3. How to take help from these solutions?

The best way is to use these solutions as reference, while one is solving the questions for practicing.

4. Are these solutions downloadable?

Yes, these questions and NCERT exemplar Class 12 Maths solutions chapter 11 can be downloaded by using the webpage to PDF tool available online.

Also Read

NCERT Class 12 Maths Notes - Download Chapter wise Free PDFs

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

JAC 12th Exam Date 2025, Check JAC Class 12 Time Table for Arts, Commerce and Science

Dec 19, 2024

IMO Cutoff 2024-25, Check SOF IMO Cut Off Marks Here

Dec 19, 2024

HBSE 2025 Exam Dates (Out), Download HBSE 10th, 12th Date Sheet PDF Here

Dec 19, 2024

CBSE Class 11 Date Sheet 2025 – Download Class 11th Exam Schedule for All Subjects

Dec 18, 2024

CBSE Class 12 English 2025: Expected Article Writing Questions to Prepare

Dec 17, 2024

Score Above 90% in CBSE Class 12 Board Exam 2025: 2-month Preparation Plan

Dec 17, 2024

CBSE Exam Rules for Class 10 and 12: New Guidelines For CBSE Exams 2024-25

Dec 13, 2024

Most Repeated Questions in Physics Class 12 CBSE Board

Dec 11, 2024

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Mock Test

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

Application Process

Exam Pattern

Admit Card

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

West Bengal Board 12th Examination

Exam Date:02 December,2024 - 20 December,2024

Result

Exam Pattern

Admit Card

Gujarat Board Secondary School Certificate Examination

Late Fee Application Date:11 December,2024 - 20 December,2024

Exam Pattern

Admit Card

Result

View All School Exams

Certifications By Top Providers

My SQL Basics

Via Great Learning

Full-Stack Web Development

Via Masai School

Business Analytics Foundations

Via PW Skills

Digital Banking Business Model

Via State Bank of India

Full-Stack Android Development

Via Masai School

Machine Learning with Python a Practical Introduction

Via IBM

1115 courses

816 courses

394 courses

295 courses

Harvard University, Cambridge

98 courses

University of Michigan, Ann Arbor

83 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

Environmental Studies

History

Psychology

Artificial Intelligence

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Delaware, Newark

Newark, DE 19716

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Cheapest and Affordable Universities in France for International Students in 2025

12 min ⋆ Dec 13, 2024 12:12 PM IST

PR in USA for International Students in 2024

7 min ⋆ Sep 16, 2024 10:09 AM IST

Top 10 Best Courses to Study in UK for Indian Students 2025

10 min ⋆ Dec 18, 2024 10:12 AM IST

Top 10 Universities in France for International Students 2025

10 min ⋆ Dec 18, 2024 10:12 AM IST

Engineering in New Zealand Fees 2025

10 min ⋆ Dec 18, 2024 10:12 AM IST

Study in Singapore - Scholarships, Cost, Best Universities, Requirements

12 min ⋆ Jul 30, 2024 12:07 PM IST

Related E-books & Sample Papers

CBSE Class 12 Accountancy Question Papers 2024 (Code-PQ1RS/1) – All Sets (1, 2, 3)

35+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-QSS4R/4) – All Sets (1, 2, 3)

36+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-Q5QPS/5) – All Sets (1, 2, 3)

14+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code- PQ3RS/3) – All Sets (1, 2, 3)

5+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-PQ2RS/2) – All Sets (1, 2, 3)

4+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-PQ1RS/1) – All Sets (1, 2, 3)

6+ Downloads

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?

quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer

Jefferson 25 September,2024

i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

Re-evaluate Your Study Strategies:
- Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
- Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
- Practice Regularly: Consistent practice is key to mastering chemistry.
Consider Professional Help:
- Tutoring: A tutor can provide personalized guidance and support.
- Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.
Explore Alternative Options:
- Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
- Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.
Focus on NEET 2025 Preparation:
- Stay Dedicated: Continue your NEET preparation with renewed determination.
- Utilize Resources: Make use of study materials, online courses, and mock tests.
Seek Support:
- Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
- Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.

Read Complete Answer

Kanishka kaushikii 17 September,2024

i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer

Yuvan 30 August,2024

i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer

Ashvadha 12 July,2024

Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer

kumardurgesh1802 10 July,2024

View All

Stay up-to date with CBSE Class 12th News

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Central Board of Secondary Education Class 12th Examination

JEE Test Series

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Exemplar Class 12th Maths Solutions Chapter 11 Three Dimensional Geometry

Main Subtopics of NCERT Exemplar Class 12 Maths Solutions Chapter 11

What will the students learn in NCERT Exemplar Class 12 Maths Solutions Chapter 11?

Pearson | PTE

NCERT Exemplar Class 12 Maths Solutions

Importance of NCERT Exemplar Class 12 Maths Solutions Chapter 11

NCERT Exemplar Class 12 Solutions

Also, check NCERT Solutions for questions given in the book:

Must Read NCERT Solution subject wise

Read more NCERT Notes subject wise

Also Check NCERT Books and NCERT Syllabus here

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Certifications By Top Providers

Explore Top Universities Across Globe

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Popular CBSE Class 12th Questions

Colleges After 12th

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Stay up-to date with CBSE Class 12th News

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

NVS

JNVST

Schools By Medium

By Ownership

By City

By State

Download Careers360 App

All this at the convenience of your phone

Scan and download the app