NCERT Solutions for Class 12 Maths Chapter 10 - Vector Algebra

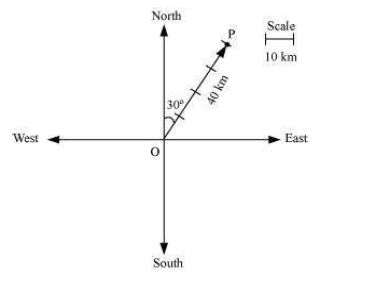
Question: 1 Represent graphically a displacement of 40 km, $30^\circ$ east of north.

Answer:

Represent graphically a displacement of 40 km, $30^\circ$ east of north.

N, S, E, W are all 4 directions: north, south, east, west, respectively.

$\overrightarrow{OP}$ is displacement vector which $\left |\overrightarrow{OP}\right |$ = 40 km.

$\overrightarrow{OP}$ makes an angle of 30 degrees east of north as shown in the figure.

Question: 2 (1) Classify the following measures as scalars and vectors.

10Kg

Answer:

10kg is a scalar quantity as it has only magnitude.

Question: 2 (2) Classify the following measures as scalars and vectors. 2 meters north west

Answer:

This is a vector quantity as it has both magnitude and direction.

Question: 2 (3) Classify the following measures as scalars and vectors. $40^\circ$

Answer:

This is a scalar quantity as it has only magnitude.

Question: 2 (4) Classify the following measures as scalars and vectors. 40 watt

Answer:

This is a scalar quantity as it has only magnitude.

Question: 2 (5) Classify the following measures as scalars and vectors. $10 ^{-19} \: \: coulomb$

Answer:

This is a scalar quantity as it has only magnitude.

Question: 2 (6) Classify the following measures as scalars and vectors. $20 m/s^2$

Answer:

This is a Vector quantity as it has magnitude as well as direction.by looking at the unit, we conclude that measure is acceleration which is a vector.

Question: 3 Classify the following as scalar and vector quantities.
(1) time period

Answer:

This is a scalar quantity as it has only magnitude.

Question: 3 Classify the following as scalar and vector quantities.

(2) distance

Answer:

Distance is a scalar quantity as it has only magnitude.

Question: 3 Classify the following as scalar and vector quantities.

(3) force

Answer:

Force is a vector quantity as it has magnitude and direction.

Question: 3 Classify the following as scalar and vector quantities.
(4) velocity

Answer:

Velocity is a vector quantity as it has both magnitude and direction.

Question: 3 Classify the following as scalar and vector quantities.

(5) work done

Answer:

Work done is a scalar quantity, as it is the product of two vectors.

Question: 4 In Fig 10.6 (a square), identify the following vectors.
(1) Coinitial

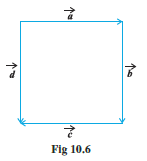
Answer:

Since vector $\vec{a}$ and vector $\vec{d}$ are starting from the same point, they are coinitial.

Question: 4 In Fig 10.6 (a square), identify the following vectors.
(2) Equal

Answer:

Since Vector $\vec{b}$ and Vector $\vec{d}$ both have the same magnitude and same direction, they are equal.

Question: 4 In Fig 10.6 (a square), identify the following vectors.

(3) Collinear but not equal

Answer:

Since vector $\vec{a}$ and vector $\vec{c}$ have the same magnitude but different direction, they are collinear and not equal.

Question: 5 Answer the following as true or false.
(1) $\vec a$ and $-\vec a$ are collinear.

Answer:

True, $\vec a$ and $-\vec a$ are collinear. they are both parallel to one line, hence they are colinear.

Question: 5 Answer the following as true or false.
(2) Two collinear vectors are always equal in magnitude.

Answer:

False, because colinear means they are parallel to the same line but their magnitude can be anything and hence, this is a false statement.

Question: 5 Answer the following as true or false.

(3) Two vectors having the same magnitude are collinear.

Answer:

False, because any two non-colinear vectors can have the same magnitude.

Question: 5 Answer the following as true or false.

(4) Two collinear vectors having the same magnitude are equal.

Answer:

False, because two collinear vectors with the same magnitude can have opposite directions.

Question: 1 Compute the magnitude of the following vectors:

(1) $\vec a = \hat i + \hat j + \hat k$

Answer:

Here

$\vec a = \hat i + \hat j + \hat k$

Magnitude of $\vec a$

$\vec a=\sqrt{1^2+1^2+1^2}=\sqrt{3}$

Question: 1 Compute the magnitude of the following vectors:

(2) $\vec b = 2 \hat i - 7 \hat j - 3 \hat k$

Answer:

Here,

$\vec b = 2 \hat i - 7 \hat j - 3 \hat k$

Magnitude of $\vec b$

$\left | \vec b \right |=\sqrt{2^2+(-7)^2+(-3)^2}=\sqrt{62}$

Question: 1 Compute the magnitude of the following vectors:

(3) $\vec c = \frac{1}{\sqrt 3 }\hat i + \frac{1}{\sqrt 3 }\hat j -\frac{1}{\sqrt 3 }\hat k$

Answer:

Here,

$\vec c = \frac{1}{\sqrt 3 }\hat i + \frac{1}{\sqrt 3 }\hat j -\frac{1}{\sqrt 3 }\hat k$

Magnitude of $\vec c$

$\left |\vec c \right |=\sqrt{\left ( \frac{1}{\sqrt{3}} \right )^2+\left ( \frac{1}{\sqrt{3}} \right )^2+\left ( \frac{1}{\sqrt{3}} \right )^2}=1$

Question: 2 Write two different vectors having the same magnitude

Answer:

Two different Vectors having the same magnitude are

$\vec a= 3\hat i+6\hat j+9\hat k$

$\vec b= 9\hat i+6\hat j+3\hat k$

The magnitude of both vector

$\left | \vec a \right |=\left | \vec b \right | = \sqrt{9^2+6^2+3^2}=\sqrt{126}$

Question: 3 Write two different vectors having the same direction.

Answer:

Two different vectors having the same direction are:

$\vec a=\hat i+2\hat j+3\hat k$

$\vec b=2\hat i+4\hat j+6\hat k$

Question: 4 Find the values of x and y so that the vectors $2 \hat i + 3 \hat j$ and $x \hat i + y \hat j$ are equal.

Answer:

$2 \hat i + 3 \hat j$ will be equal to $x \hat i + y \hat j$ when their corresponding components are equal.

Hence when,

$x=2$ and $y=3$

Question: 5 Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (– 5, 7).

Answer:

Let point P = (2, 1) and Q = (– 5, 7).

Now,

$\vec {PQ}=(-5-2)\hat i+(7-1)\hat j=-7\hat i +6\hat j$

Hence, scalar components are (-7,6) and the vector is $-7\hat i +6\hat j$

Question: 6 Find the sum of the vectors $\vec a = \hat i - 2 \hat j + \hat k , \vec b = -2 \hat i + 4 \hat j + 5 \hat k \: \: and\: \: \: \vec c = \hat i - 6 \hat j - 7 \hat k$

Answer:

Given,

$\vec a = \hat i - 2 \hat j + \hat k ,\\ \vec b = -2 \hat i + 4 \hat j + 5 \hat k \: \: and\: \: \: \\\vec c = \hat i - 6 \hat j - 7 \hat k$

Now, The sum of the vectors:

$\vec a +\vec b+\vec c = \hat i - 2 \hat j + \hat k + -2 \hat i + 4 \hat j + 5 \hat k + \hat i - 6 \hat j - 7 \hat k$

$\vec a +\vec b+\vec c = (1-2+1)\hat i +(-2+4-6) \hat j + (1+5-7)\hat k$

$\vec a +\vec b+\vec c =-4\hat j-\hat k$

Question: 7 Find the unit vector in the direction of the vector $\vec a = \hat i + \hat j + 2 \hat k$

Answer:

Given

$\vec a = \hat i + \hat j + 2 \hat k$

Magnitude of $\vec a$

$\left |\vec a \right |=\sqrt{1^2+1^2+2^2}=\sqrt{6}$

A unit vector in the direction of $\vec a$

$\vec u = \frac{\hat i}{\left | a \right |} + \frac{\hat j}{\left | a \right |} +\frac{2\hat k}{\left | a \right |} =\frac{\hat i}{\sqrt{6}}+\frac{\hat j}{\sqrt{6}}+\frac{2\hat k}{\sqrt{6}}$

Question: 8 Find the unit vector in the direction of vector $\vec { PQ}$ , where P and Q are the points (1, 2, 3) and (4, 5, 6), respectively.

Answer:

Given P = (1, 2, 3) and Q = (4, 5, 6)

A vector in the direction of PQ

$\vec {PQ}=(4-1)\hat i+(5-2)\hat j +(6-3)\hat k$

$\vec {PQ}=3\hat i+3\hat j +3\hat k$

Magnitude of PQ

$\left | \vec {PQ} \right |=\sqrt{3^2+3^2+3^2}=3\sqrt{3}$

Now, the unit vector in the direction of PQ

$\hat u=\frac{\vec {PQ}}{\left | \vec {PQ} \right |}=\frac{3\hat i+3\hat j+3\hat k}{3\sqrt{3}}$

$\hat u=\frac{\hat i}{\sqrt{3}}+\frac{\hat j}{\sqrt{3}}+\frac{\hat k}{\sqrt{3}}$

Question: 9 For given vectors, $\vec a = 2 \hat i - \hat j + 2 \hat k$ and $\vec b = - \hat i + \hat j - \hat k$ , find the unit vector in the direction of the vector $\vec a + \vec b$ .

Answer:

Given

$\vec a = 2 \hat i - \hat j + 2 \hat k$

$\vec b = - \hat i + \hat j - \hat k$

Now,

$\vec a + \vec b=(2-1)\hat i+(-1+1)\hat j+ (2-1)\hat k$

$\vec a + \vec b=\hat i+\hat k$

Now a unit vector in the direction of $\vec a + \vec b$

$\vec u= \frac{\vec a + \vec b}{\left |\vec a + \vec b \right |}=\frac{\hat i+\hat j}{\sqrt{1^2+1^2}}$

$\vec u= \frac{\hat i}{\sqrt{2}}+\frac{\hat j}{\sqrt{2}}$

Question: 10 Find a vector in the direction of vector $5 \hat i - \hat j + 2 \hat k$ which has magnitude 8 units.

Answer:

Given a vector

$\vec a=5 \hat i - \hat j + 2 \hat k$

the unit vector in the direction of $5 \hat i - \hat j + 2 \hat k$

$\vec u=\frac{5\hat i - \hat j + 2 \hat k}{\sqrt{5^2+(-1)^2+2^2}}=\frac{5\hat i}{\sqrt{30}}-\frac{\hat j}{\sqrt{30}}+\frac{2\hat k}{\sqrt{30}}$

A vector in direction of $5 \hat i - \hat j + 2 \hat k$ and whose magnitude is 8 =

$8\vec u=\frac{40\hat i}{\sqrt{30}}-\frac{8\hat j}{\sqrt{30}}+\frac{16\hat k}{\sqrt{30}}$

Question: 1 Find the angle between two vectors $\vec a \: \:and \: \: \vec b$ with magnitudes $\sqrt 3 \: \:and \: \: 2$ , respectively having . $\vec a . \vec b = \sqrt 6$

Answer:

Given

$\left | \vec a \right |=\sqrt{3}$

$\left | \vec b \right |=2$

$\vec a . \vec b = \sqrt 6$

As we know

$\vec a . \vec b = \left | \vec a \right |\left | \vec b \right |cos\theta$

where $\theta$ is the angle between two vectors

So,

$cos\theta =\frac{\vec a.\vec b}{\left | \vec a \right |\left | \vec b \right |}=\frac{\sqrt{6}}{\sqrt{3}×2}=\frac{1}{\sqrt{2}}$

$\theta=\frac{\pi}{4}$

Hence, the angle between the vectors is $\frac{\pi}{4}$.

Question: 2 Find the angle between the vectors $\hat i - 2 \hat j + 3 \hat k \: \:and \: \: 3 \hat i - 2 \hat j + \hat k$

Answer:

Given two vectors

$\vec a=\hat i - 2 \hat j + 3 \hat k \: \:and \: \: \vec b=3 \hat i - 2 \hat j + \hat k$

Now, As we know,

The angle between two vectors $\vec a$ and $\vec b$ is given by

$\theta=cos^{-1}\left ( \frac{\vec a.\vec b}{\left | \vec a \right |\left | \vec b \right |}\right )$

Hence the angle between $\vec a=\hat i - 2 \hat j + 3 \hat k \: \:and \: \: \vec b=3 \hat i - 2 \hat j + \hat k$

⇒ $\theta=cos^{-1}\left ( \frac{(\hat i-2\hat j+3\hat k).(3\hat i-2\hat j+\hat k)}{\left | \hat i-2\hat j+3\hat k \right |\left |3\hat i-2\hat j+\hat k \right |}\right )$

⇒ $\theta=cos^{-1}\left ( \frac{3+4+3}{\sqrt{1^2+(-2)^2+3^3}\sqrt{3^2+(-2)^2+1^2}} \right )$

⇒ $\theta=cos^{-1}\frac{10}{14}$

⇒ $\theta=cos^{-1}\frac{5}{7}$

Question: 3 Find the projection of the vector $\hat i - \hat j$ on the vector $\hat i + \hat j$

Answer:

Let

$\vec a=\hat i - \hat j$

$\vec b=\hat i + \hat j$

Projection of vector $\vec a$ on $\vec b$

$\frac{\vec a.\vec b}{\left | \vec b \right |}=\frac{(\hat i-\hat j)(\hat i+\hat j)}{\left |\hat i+\hat j \right |}=\frac{1-1}{\sqrt{2}}=0$

Hence, the Projection of vector $\vec a$ on $\vec b$ is 0.

Question: 4 Find the projection of the vector $\hat i + 3 \hat j + 7 \hat k$ on the vector $7\hat i - \hat j + 8 \hat k$

Answer:

Let

$\vec a =\hat i + 3 \hat j + 7 \hat k$

$\vec b=7\hat i - \hat j + 8 \hat k$

The projection of $\vec a$ on $\vec b$ is

$\frac{\vec a.\vec b}{\left | \vec b \right |}=\frac{(\hat i+3\hat j+7\hat k)(7\hat i-\hat j+8\hat k)}{\left | 7\hat i-\hat j+8\hat k \right |}=\frac{7-3+56}{\sqrt{7^2+(-1)^2+8^2}}=\frac{60}{\sqrt{114}}$

Hence, projection of vector $\vec a$ on $\vec b$ is $\frac{60}{\sqrt{114}}$.

Question: 5 Show that each of the given three vectors is a unit vector: $\frac{1}{7}( 2 \hat i + 3 \hat j + 6 \hat k ), \frac{1}{7}( 3 \hat i- 6 \hat j + 2 \hat k ), \frac{1}{7}( 6\hat i + 2 \hat j -3\hat k )$ Also, show that they are mutually perpendicular to each other.

Answer:

Given

$\vec a=\frac{1}{7}( 2 \hat i + 3 \hat j + 6 \hat k ), \\\ \vec b =\frac{1}{7}( 3 \hat i- 6 \hat j + 2 \hat k ),\\\vec c = \frac{1}{7}( 6\hat i + 2 \hat j -3\hat k )$

Now magnitude of $\vec a,\vec b \:and\: \vec c$

$\left | \vec a \right |=\frac{1}{7} \sqrt{2^2+3^2+6^2}=\frac{\sqrt{49}}{7}=1$

$\left | \vec b \right |=\frac{1}{7} \sqrt{3^2+(-6)^2+2^2}=\frac{\sqrt{49}}{7}=1$

$\left | \vec c \right |=\frac{1}{7} \sqrt{6^2+2^2+(-3)^2}=\frac{\sqrt{49}}{7}=1$

Hence, they are all unit vectors.

Now,

$\vec a.\vec b=\frac{1}{7}(2\hat i+3\hat j+6\hat k)\frac{1}{7}(3\hat i-6\hat j+2\hat k)=\frac{1}{49}(6-18+12)=0$

$\vec b.\vec c=\frac{1}{7}(3\hat i-6\hat j+2\hat k)\frac{1}{7}(6\hat i+2\hat j-3\hat k)=\frac{1}{49}(18-12-6)=0$

$\vec c.\vec a=\frac{1}{7}(6\hat i+2\hat j-3\hat k)\frac{1}{7}(2\hat i+3\hat j-6\hat k)=\frac{1}{49}(12+6-18)=0$

Hence, all three are mutually perpendicular to each other.

Question: 6 Find $|\vec a| \: \: and\: \:| \vec b |$ , if $( \vec a + \vec b ). ( \vec a - \vec b )=8 \: \:and \: \: |\vec a |\: \:= 8 \: \:|\vec b |$ .

Answer:

Given in the question

$( \vec a + \vec b ). ( \vec a - \vec b )=8$

$\left | \vec a \right |^2-\left | \vec b \right |^2=8$

Since $|\vec a |\: \:= 8 \: \:|\vec b |$

⇒ $\left | \vec {8b} \right |^2-\left | \vec b \right |^2=8$

⇒ $\left | \vec {63b} \right |^2=8$

⇒ $\left | \vec {b} \right |^2=\frac{8}{63}$

⇒ $\left | \vec {b} \right |=\sqrt{\frac{8}{63}}$

So, the answer is

$\left | \vec {a} \right |=8\left | \vec {b} \right |=8\sqrt{\frac{8}{63}}$

Question: 7 Evaluate the product $( 3\vec a - 5 \vec b ). ( 2 \vec a + 7 \vec b )$ .

Answer:

To evaluate the product $( 3\vec a - 5 \vec b ). ( 2 \vec a + 7 \vec b )$

$( 3\vec a - 5 \vec b ). ( 2 \vec a + 7 \vec b )=6\vec a.\vec a+21\vec a.\vec b-10\vec b.\vec a-35\vec b.\vec b$

$=6\vec a.^2+11\vec a.\vec b-35\vec b^2$

$=6\left | \vec a \right |^2+11\vec a.\vec b-35\left | \vec b \right |^2$

Question: 8 Find the magnitude of two vectors $\vec a \: \: and \: \: \vec b$ , having the same magnitude and such that the angle between them is $60 ^\circ$ and their scalar product is 1/2

Answer:

Given two vectors $\vec a \: \: and \: \: \vec b$

$\left | \vec a \right |=\left | \vec b\right |$

$\vec a.\vec b=\frac{1}{2}$

Now Angle between $\vec a \: \: and \: \: \vec b$

$\theta=60^0$

Now, As we know that

$\vec a.\vec b=\left | \vec a \right |\left | \vec b \right |cos\theta$

$\frac{1}{2}=\left | \vec a \right |\left | \vec a \right |cos60^0$

$\left | a \right |^2=1$

Hence, the magnitude of two vectors $\vec a \: \: and \: \: \vec b$

$\left | a \right |=\left | b \right |=1$

Question: 9 Find $|\vec x |$ , if for a unit vector $\vec a , ( \vec x -\vec a ) . ( \vec x + \vec a ) = 12$

Answer:

Given in the question that

$( \vec x -\vec a ) . ( \vec x + \vec a ) = 12$

And we need to find $\left | \vec x \right |$

$\left | \vec x \right |^2-\left | \vec a \right |^2 = 12$

⇒ $\left | \vec x \right |^2-1 = 12$

⇒ $\left | \vec x \right |^2 = 13$

⇒ $\left | \vec x \right | = \sqrt{13}$

So the value of $\left | \vec x \right |$ is $\sqrt{13}$.

Question:1 Find $|\vec a \times \vec b |,\ if \ \vec a = \hat i - 7 \hat j + 7 \hat k \: \: and \: \: \vec b = 3 \hat i - 2 \hat j + 2 \hat k$.

Answer:
Given in the question,

$\\ \vec a = \hat i - 7 \hat j + 7 \hat k \: \: and \: \: \\\vec b = 3 \hat i - 2 \hat j + 2 \hat k$

and we need to find $|\vec a \times \vec b |$

Now,

$|\vec a \times \vec b | =\begin{vmatrix} \hat i &\hat j &\hat k \\ 1 &-7 &7 \\ 3& -2 &2 \end{vmatrix}$

⇒ $|\vec a \times \vec b | =\hat i(-14+14)-\hat j(2-21)+\hat k(-2+21)$

⇒ $|\vec a \times \vec b | =19\hat j+19\hat k$

So, the value of $|\vec a \times \vec b |$ is $19\hat j+19\hat k$.

Question:2 Find a unit vector perpendicular to each of the vector $\vec a + \vec b \: \: and\: \: \vec a - \vec b$ , where $\vec a = 3 \hat i + 2 \hat j + 2 \hat k \: \:and \: \: \vec b = \hat i + 2 \hat j - 2 \hat k$.

Answer:
Given in the question

$\vec a = 3 \hat i + 2 \hat j + 2 \hat k \: \:and \: \: \vec b = \hat i + 2 \hat j - 2 \hat k$

$\vec a + \vec b =3\hat i +2\hat j+2\hat k+\hat i +2\hat j-2\hat k=4\hat i +4\hat j$

$\vec a - \vec b =3\hat i +2\hat j+2\hat k-\hat i -2\hat j+2\hat k=2\hat i +4\hat k$

Now , A vector which perpendicular to both $\vec a + \vec b \: \: and\: \: \vec a - \vec b$ is $(\vec a + \vec b) \times (\vec a - \vec b)$

$(\vec a + \vec b) \times (\vec a - \vec b)=\begin{vmatrix} \hat i &\hat j &\hat k \\ 4&4 &0 \\ 2& 0& 4 \end{vmatrix}$

⇒ $(\vec a + \vec b) \times (\vec a - \vec b)= \hat i (16-0)-\hat j(16-0)+\hat k(0-8)$

⇒ $(\vec a + \vec b) \times (\vec a - \vec b)= 16\hat i -16\hat j-8\hat k$

And a unit vector in this direction :

$\vec u =\frac{16\hat i-16\hat j-8\hat k}{|16\hat i-16\hat j-8\hat k|}=\frac{16\hat i-16\hat j-8\hat k}{\sqrt{16^2+(-16)^2+(-8)^2}}$

⇒ $\vec u =\frac{16\hat i-16\hat j-8\hat k}{24}=\frac{2}{3}\hat i-\frac{2}{3}\hat j-\frac{1}{3}\hat k$

Hence, Unit vector perpendicular to each of the vector $\vec a + \vec b \: \: and\: \: \vec a - \vec b$ is $\frac{2}{3}\hat i-\frac{2}{3}\hat j-\frac{1}{3}\hat k$.

Question:3 If a unit vector $\vec a$ makes angles $\frac{\pi }{3}$ with $\hat i , \frac{\pi }{4}$ with $\hat j$ and an acute angle $\theta$ with $\hat k$ then find $\theta$ and hence, the components of $\vec a$.

Answer:
Given in the question,

Angle between $\vec a$ and $\hat i$ :

$\alpha =\frac{\pi}{3}$

Angle between $\vec a$ and $\hat j$

$\beta =\frac{\pi}{4}$

Angle with $\vec a$ and $\hat k$ :

$\gamma =\theta$

Now, as we know,

$cos^2\alpha+cos^2\beta+cos^2\gamma=1$

⇒ $cos^2\frac{\pi}{3}+cos^2\frac{\pi }{4}+cos^2\theta=1$

⇒ $\left ( \frac{1}{2} \right )^2+\left ( \frac{1}{\sqrt{2}} \right )^2+cos^2\theta=1$

⇒ $cos^2\theta=\frac{1}{4}$

⇒ $cos\theta=\frac{1}{2}$ (As $\theta$ is acute)

⇒ $\theta=\frac{\pi}{3}$

Now, components of $\vec a$ are:

$\left ( cos\frac{\pi}{3},cos\frac{\pi}{2},cos\frac{\pi}{3} \right )=\left ( \frac{1}{2},\frac{1}{\sqrt{2}},\frac{1}{2} \right )$.

Question:4 Show that $( \vec a - \vec b ) \times (\vec a + \vec b ) = 2 ( \vec a \times \vec b )$

Answer:
To show that $( \vec a - \vec b ) \times (\vec a + \vec b ) = 2 ( \vec a \times \vec b )$

LHS

$( \vec a - \vec b ) \times (\vec a + \vec b )=( \vec a - \vec b ) \times (\vec a)+( \vec a - \vec b ) \times (\vec b)$

⇒ $( \vec a - \vec b ) \times (\vec a + \vec b )= \vec a \times \vec a-\vec b \times\vec a+\vec a \times \vec b-\vec b \times \vec b$

As product of a vector with itself is always Zero,

$( \vec a - \vec b ) \times (\vec a + \vec b )= 0-\vec b \times\vec a+\vec a \times \vec b-0$

As cross product of a and b is equal to negative of cross product of b and a.

$( \vec a - \vec b ) \times (\vec a + \vec b )= \vec a \times\vec b+\vec a \times \vec b$

⇒ $( \vec a - \vec b ) \times (\vec a + \vec b )= 2(\vec a \times\vec b)$ = RHS

LHS is equal to RHS, Hence Proved.

Question:5 Find $\lambda$ and $\mu$ if $( 2 \hat i + 6 \hat j + 27 \hat k ) \times ( \hat i + \lambda j + \mu \hat k ) = \vec 0$

Answer:
Given in the question

$(2 \hat i + 6 \hat j + 27 \hat k ) \times ( \hat i + \lambda j + \mu \hat k ) = \vec 0$

and we need to find values of $\lambda$ and $\mu$.

⇒ $\begin{vmatrix} \hat i &\hat j & \hat k\\ 2& 6&27 \\ 1& \lambda &\mu \end{vmatrix}=0$

⇒ $\hat i (6\mu-27\lambda)-\hat j(2\mu-27)+\hat k(2\lambda-6)=0$

From here we get,

$6\mu-27\lambda=0$

$2\mu-27=0$ ⇒ $\mu=\frac{27}{2}$

$2\lambda -6=0$ ⇒ $\lambda = 3$

From here, the value of $\lambda$ and $\mu$ is

$\lambda = 3 , \: and \: \mu=\frac{27}{2}$.

Question:6 Given that $\vec a . \vec b = 0 \: \:and \: \: \vec a \times \vec b = 0$ and . What can you conclude about the vectors $\vec a \: \:and \: \: \vec b$ ?

Answer:
Given in the question

$\vec a . \vec b = 0$ and $\vec a \times \vec b = 0$

When $\vec a . \vec b = 0$ , either $|\vec a| =0,\:or\: |\vec b|=0,\:or\: \vec a\: and \:\vec b$ are perpendicular to each other.

When $\vec a \times \vec b = 0$ either $|\vec a| =0,\:or\: |\vec b|=0,\:or\: \vec a\: and \:\vec b$ are parallel to each other.

Since two vectors can never be both parallel and perpendicular at the same time,

We conclude that

$|\vec a| =0\:or\: |\vec b|=0$.

Question:7 Let the vectors $\vec a , \vec b , \vec c$ be given as $\vec a_1 \hat i + \vec a_2 \hat j + \vec a_3 \hat k , \vec b_ 1 \hat i + \vec b_ 2 \hat j + \vec b_3 \hat k , \vec c_ 1 \hat i + \vec c_ 2 \hat j + \vec c_ 3 \hat k$ Then show that $\vec a \times ( \vec b + \vec c ) = \vec a \times \vec b + \vec a \times \vec c$

Answer:
Given in the question

$\\\vec a=\vec a_1 \hat i + \vec a_2 \hat j + \vec a_3 \hat k , \\\vec b=\vec b_ 1 \hat i + \vec b_ 2 \hat j + \vec b_3 \hat k , \\\vec c=\vec c_ 1 \hat i + \vec c_ 2 \hat j + \vec c_ 3 \hat k$

We need to show that $\vec a \times ( \vec b + \vec c ) = \vec a \times \vec b + \vec a \times \vec c$

Now, $\vec a \times ( \vec b + \vec c ) =(\vec a_1 \hat i + \vec a_2 \hat j + \vec a_3 \hat k)\times(\vec b_ 1 \hat i + \vec b_ 2 \hat j + \vec b_3 \hat k +\vec c_ 1 \hat i + \vec c_ 2 \hat j + \vec c_ 3 \hat k)$

$=(\vec a_1 \hat i + \vec a_2 \hat j + \vec a_3 \hat k)\times((\vec b_ 1+\vec c_1) \hat i + (\vec b_ 2+\vec c_2) \hat j +( \vec b_3 +\vec c_3)\hat k)$

$=\begin{vmatrix} \hat i &\hat j &\hat k \\ a_1&a_2 &a_3 \\ (b_1+c_1)&(b_2+c_2) &(b_3+c_3) \end{vmatrix}$

$=\hat i(a_2(b_3+c_3)-a_3(b_2+c_2))-\hat j(a_1(b_3+c_3)- a_3(b_1+c_1))+\hat k (a_1(b_2+c_2)-a_2(a_1(b_2+c_3)))$

$=\hat i(a_2(b_3+c_3)-a_3(b_2+c_2))-\hat j(a_1(b_3+c_3)-a_3(b_1+c_1))+\hat k (a_1(b_2+c_2)-a_2(a_1(b_2+c_3)))$

Now, $\vec a \times \vec b + \vec a \times \vec c=\begin{vmatrix} \hat i &\hat j & \hat k\\ a_1&a_2 &a_3 \\ b_1&b_2 &b_3 \end{vmatrix}+\begin{vmatrix} \hat i &\hat j & \hat k\\ a_1&a_2 &a_3 \\ c_1&c_2 &c_3 \end{vmatrix}$

$\vec a \times \vec b + \vec a \times \vec c=\hat i(a_2b_3-a_3b_2)-\hat j (a_1b_3-a_3b_1)+\hat k(a_1b_2-b_1a_2)+\hat i(a_2c_3-a_3c_2)-\hat j (a_1c_3-a_3c_1)+\hat k(a_1c_2-c_1a_2)$

$=\hat i(a_2(b_3+c_3)-a_3(b_2+c_2))-\hat j(a_1(b_3+c_3)-a_3(b_1+c_1))+\hat k (a_1(b_2+c_2)-a_2(a_1(b_2+c_3)))$

Hence, they are equal.

Question:8 If either $\vec a = \vec 0 \: \: or \: \: \vec b = \vec 0$ then $\vec a \times \vec b = \vec 0$ . Is the converse true? Justify your answer with an example.

Answer:
No, the converse of the statement is not true, as there can be two non-zero vectors, the cross product of whose is zero; they are collinear vectors.

Consider an example

$\vec a=\hat i +\hat j + \hat k$

$\vec b =2\hat i +2\hat j + 2\hat k$

Here $|\vec a| =\sqrt{1^2+1^2+1^2}=\sqrt{3}$

$|\vec b| =\sqrt{2^2+2^2+2^2}=2\sqrt{3}$

$\vec a \times \vec b=\begin{vmatrix} \hat i &\hat j &\hat k \\ 1&1 &1 \\ 2&2 &2 \end{vmatrix}=\hat i(2-2)-\hat j(2-2)+\hat k(2-2)=0$

Hence, the converse of the given statement is not true.

Question:9 Find the area of the triangle with vertices A(1, 1, 2), B(2, 3, 5) and C(1, 5, 5).

Answer:
Given in the question

Vertices A = (1, 1, 2), B = (2, 3, 5) and C = (1, 5, 5). We need to find the area of the triangle

$AB=(2-1)\hat i+(3-1)\hat j+(5-2)\hat k=\hat i+2\hat j+3\hat k$

$BC=(1-2)\hat i+(5-3)\hat j+(5-5)\hat k=-\hat i+2\hat j$

Now, as we know

Area of the triangle,

$A=\frac{1}{2}|\vec {AB}\times\vec {BC}|=\frac{1}{2}|(\hat i+2\hat j +3\hat k)\times(-\hat i+2\hat j)|$

$=\frac{1}{2}\begin{vmatrix} \hat i &\hat j &\hat k \\ 1 &2 &3 \\ -1 &2 &0 \end{vmatrix}=\frac{1}{2}|\hat i(0-6)-\hat j(0-(-3))+\hat k(2-(-2))|$

$=\frac{1}{2}|-6\hat i-3\hat j+4\hat k|$

$=\frac{1}{2}×\sqrt{(-6)^2+(-3)^2+(4)^2}=\frac{\sqrt{61}}{2}$

So, the area of the triangle is $\frac{\sqrt{61}}{2}$ square units.

Question: 10 Find the area of the parallelogram whose adjacent sides are determined by the vectors $\vec a = \hat i - \hat j + 3 \hat k$ and $\vec b = 2\hat i -7 \hat j + \hat k$.

Answer:
Given in the question

$\vec a = \hat i - \hat j + 3 \hat k$

$\vec b = 2\hat i -7 \hat j + \hat k$

Area of parallelogram with adjescent side $\vec a$ and $\vec b$ ,

$A=|\vec a\times\vec b|=|(\vec i-\vec j+3\vec k)\times (2\hat i-7\hat j+\hat k)|$

$=\begin{vmatrix} \hat i& \hat j & \hat k\\ 1&-1 &3 \\ 2&-7 &1 \end{vmatrix}=|\hat i(-1+21)-\hat j (1-6)+\hat k (-7+2)|$

$=|\hat i(20)-\hat j (-5)+\hat k (-5)|=\sqrt{20^2+5^2+(-5)^2}$

$=\sqrt{450}=15\sqrt{2}$

So, the area of the parallelogram whose adjacent sides are determined by the vectors $\vec a = \hat i - \hat j + 3 \hat k$ and $\vec b = 2\hat i -7 \hat j + \hat k$ is $A=\sqrt{450}=15\sqrt{2}$ square units.

Question: 11 Let the vectors $\vec a \: \: and\: \: \vec b$ be such that $|\vec a| = 3 \: \: and\: \: |\vec b | = \frac{\sqrt 2 }{3}$ , then $\vec a \times \vec b$ is a unit vector, if the angle between $\vec a \: \:and \: \: \vec b$ is

$\\A ) \pi /6 \ B ) \pi / 4 \ C ) \pi / 3 \ D ) \pi /2$

Answer:
Given in the question,

$|\vec a| = 3 \: \: and\: \: |\vec b | = \frac{\sqrt 2 }{3}$

As given $\vec a \times \vec b$ is a unit vector, which means,

$|\vec a \times \vec b|=1$

⇒ $|\vec a| | \vec b|sin\theta=1$

⇒ $3×\frac{\sqrt{2}}{3}sin\theta=1$

⇒ $sin\theta=\frac{1}{\sqrt{2}}$

⇒ $\theta=\frac{\pi}{4}$

Hence, the angle between two vectors is $\frac{\pi}{4}$. The correct option is B.

Question: 12 Area of a rectangle having vertices A, B, C and D with position vectors

$- \hat i + \frac{1}{2} \hat j + 4 \hat k , \hat i + \frac{1}{2} \hat j + 4 \hat k , \hat i - \frac{1}{2}\hat j + 4 \hat k \: \: and \: \: - \hat i - \frac{1}{2} \hat j + 4 \hat k$

(A) $\frac{1}{2}$

(B) 1

(C) 2

(D) 4

Answer:
Given the four vertices of a rectangle are,

$\\\vec a=- \hat i + \frac{1}{2} \hat j + 4 \hat k , \\\vec b=\hat i + \frac{1}{2} \hat j + 4 \hat k , \\\vec c= \hat i - \frac{1}{2}\hat j + 4 \hat k \: \: and \: \: \\\vec d= - \hat i - \frac{1}{2} \hat j + 4 \hat k$

$\vec {AB}=\vec b-\vec a=(1+1)\hat i+(\frac{1}{2}-\frac{1}{2})\hat j+(4-4)\hat k=2\hat i$

$\vec {BC}=\vec c-\vec b=(1-1)\hat i+(-\frac{1}{2}-\frac{1}{2})\hat j+(4-4)\hat k=-\hat j$

Now, the Area of the Rectangle

$A=|\vec {AB}\times\vec {BC}|=|2\hat i \times (-\hat j)|=2$

Hence, option C is correct.

Question: 11 Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are $\pm \left ( \frac{1}{\sqrt 3 } , \frac{1}{\sqrt 3 } , \frac{1}{\sqrt 3 } \right )$

Answer:

Let a vector $\vec a$ is equally inclined to axis OX, OY and OZ.

let direction cosines of this vector be

$cos\alpha,cos\alpha \:and \:cos\alpha$

Now

$cos^2\alpha+cos^2\alpha +cos^2\alpha=1$

$cos^2\alpha=\frac{1}{3}$

$cos\alpha=\frac{1}{\sqrt{3}}$

Hence, direction cosines are:

$\left ( \frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}},\frac{1}{\sqrt{3}} \right )$.

Question: 12 Let $\vec a = \hat i + 4 \hat j + 2 \hat k , \vec b = 3 \hat i - 2 \hat j + 7 \hat k \: \:and \: \: \vec c = 2 \hat i - \hat j + 4 \hat k$ . Find a vector $\vec d$ which is perpendicular to both $\vec a \: \: and \: \: \vec b \: \: and \: \: \vec c . \vec d = 15$

Answer:

Given,

$\vec a = \hat i + 4 \hat j + 2 \hat k , \vec b = 3 \hat i - 2 \hat j + 7 \hat k \: \:and \: \: \vec c = 2 \hat i - \hat j + 4 \hat k$

Let $\vec d=d_1\hat i+d_2\hat j +d_3\hat k$

now, since it is given that d is perpendicular to $\vec a$ and $\vec b$ , we got the condition,

$\vec b.\vec d=0$ and $\vec a.\vec d=0$

$(\hat i+4\hat j +2\hat k)\cdot(d_1\hat i +d_2\hat j+d_3\hat k)=0$ And $(3\hat i-2\hat j +7\hat k)\cdot(d_1\hat i +d_2\hat j+d_3\hat k)=0$

$d_1+4d_2+2d_3=0$ And $3d_1-2d_2+7d_3=0$

here we got 2 equation and 3 variable. one more equation will come from the condition:

$\vec c . \vec d = 15$

$(2\hat i-\hat j +4\hat k)\cdot(d_1\hat i +d_2\hat j+d_3\hat k)=15$

$2d_1-d_2+4d_3=15$

so now we have three equation and three variable,

$d_1+4d_2+2d_3=0$

$3d_1-2d_2+7d_3=0$

$2d_1-d_2+4d_3=15$

On solving this three equation we get,

$d_1=\frac{160}{3},d_2=-\frac{5}{3}\:and\:d_3=-\frac{70}{3}$ ,

Hence, Required vector :

$\vec d=\frac{160}{3}\hat i-\frac{5}{3}\hat j-\frac{70}{3}\hat k$.

Question: 13 The scalar product of the vector $\hat i + \hat j + \hat k$ with a unit vector along the sum of vectors $2\hat i + 4 \hat j -5 \hat k$ and $\lambda \hat i + 2 \hat j +3 \hat k$ is equal to one. Find the value of $\lambda$ .

Answer:

Let, the sum of vectors $2\hat i + 4 \hat j -5 \hat k$ and $\lambda \hat i + 2 \hat j +3 \hat k$ be

$\vec a=(\lambda +2)\hat i + 6 \hat j -2 \hat k$

unit vector along $\vec a$

$\vec u=\frac{(\lambda +2)\hat i + 6 \hat j -2 \hat k}{\sqrt{(\lambda+2)^2+6^2+(-2)^2}}=\frac{(\lambda +2)\hat i + 6 \hat j -2 \hat k}{\sqrt{\lambda^2+4\lambda+44}}$

Now, the scalar product of this with $\hat i + \hat j + \hat k$

$\vec u.(\hat i+\hat j +\hat k)=\frac{(\lambda +2)\hat i + 6 \hat j -2 \hat k}{\sqrt{\lambda^2+4\lambda+44}}.(\hat i+\hat j +\hat k)$

$\vec u.(\hat i+\hat j +\hat k)=\frac{(\lambda +2) + 6 -2 }{\sqrt{\lambda^2+4\lambda+44}}=1$

$\frac{(\lambda +2) + 6 -2 }{\sqrt{\lambda^2+4\lambda+44}}=1$

$\frac{(\lambda +6) }{\sqrt{\lambda^2+4\lambda+44}}=1$

$\lambda =1$

Question: 14 If $\vec a , \vec b , \vec c$ are mutually perpendicular vectors of equal magnitudes, show that the vector $\vec a+\vec b +\vec c$ is equally inclined to $\vec a , \vec b \: \: and \: \: \vec c$ .

Answer:

Given

$|\vec a|=|\vec b|=|\vec c|$ and

$\vec a.\vec b=\vec b.\vec c=\vec c.\vec a=0$

Now, let vector $\vec a+\vec b +\vec c$ is inclined to $\vec a , \vec b \: \: and \: \: \vec c$ at $\theta_1,\theta_2\:and\:\theta_3$ respectively.

Now,

$cos\theta_1=\frac{(\vec a+\vec b+\vec c).\vec a}{|\vec a+\vec b+\vec c||\vec a|}=\frac{\vec a.\vec a +\vec a.\vec b +\vec c.\vec a}{|\vec a+\vec b+\vec c||\vec a|}=\frac{\vec a.\vec a}{|\vec a+\vec b+\vec c||\vec a|}=\frac{|\vec a|}{|\vec a+\vec b+\vec c|}$

$cos\theta_2=\frac{(\vec a+\vec b+\vec c).\vec b}{|\vec a+\vec b+\vec c||\vec b|}=\frac{\vec a.\vec b +\vec b.\vec b +\vec c.\vec b}{|\vec a+\vec b+\vec c||\vec b|}=\frac{\vec b.\vec b}{|\vec a+\vec b+\vec c||\vec b|}=\frac{|\vec b|}{|\vec a+\vec b+\vec c|}$

$cos\theta_3=\frac{(\vec a+\vec b+\vec c).\vec c}{|\vec a+\vec b+\vec c||\vec c|}=\frac{\vec a.\vec c +\vec b.\vec c +\vec c.\vec c}{|\vec a+\vec b+\vec c||\vec c|}=\frac{\vec c.\vec c}{|\vec a+\vec b+\vec c||\vec c|}=\frac{|\vec c|}{|\vec a+\vec b+\vec c|}$

Now, Since, $|\vec a|=|\vec b|=|\vec c|$

$cos\theta_1=cos\theta_2=cos\theta_3$

$\theta_1=\theta_2=\theta_3$

Hence vector $\vec a+\vec b +\vec c$ is equally inclined to $\vec a , \vec b \: \: and \: \: \vec c$.

Question: 15 Prove that $( \vec a + \vec b ) . (\vec a + \vec b ) = |\vec a ^2 | + |\vec b |^2$ , if and only if $\vec a , \vec b$ are perpendicular, given $\vec a \neq 0 , \vec b \neq 0$

Answer:

Given in the question,

are perpendicular and we need to prove that

LHS=

if are perpendicular,

= RHS

LHS is equal to RHS.

Hence proved.

Question: 16 Choose the correct answer If $\theta$ is the angle between two vectors $\vec a \: \: and \: \: \vec b$ , then $\vec a \cdot \vec b \geq 0$ only when
$\\A ) 0 < \theta < \frac{\pi }{2} \\\\ \: \: \: \: B ) 0 \leq \theta \leq \frac{\pi }{2} \\\\ \: \: \: C ) 0 < \theta < \pi \\\\ \: \: \: D) 0 \leq \theta \leq\pi$

Answer:

Given in the question

$\theta$ is the angle between two vectors $\vec a \: \: and \: \: \vec b$

$\vec a \cdot \vec b \geq 0$

$|\vec a| | \vec b |cos\theta\geq 0$

this will satisfy when

$cos\theta\geq 0$

$0\leq\theta\leq \frac{\pi}{2}$

Hence, option B is the correct answer.

Question 17 Choose the correct answer. Let $\vec a \: \: and \: \: \vec b$ be two unit vectors and $\theta$ is the angle between them. Then $\vec a + \vec b$ is a unit vector if

$\\A ) \theta = \frac{\pi }{4} \\\\ B ) \theta = \frac{\pi }{3} \\\\ C ) \theta = \frac{\pi }{2} \\\\ D ) \theta = \frac{2\pi }{3}$

Answer:

Given in the question

$\vec a \: \: and \: \: \vec b$ be two unit vectors and $\theta$ is the angle between them

$|\vec a|=1,\:and\:\:|\vec b|=1$

also

$|\vec a + \vec b|=1$

$|\vec a + \vec b|^2=1$

$|\vec a|^2 + |\vec b|^2+2\vec a.\vec b=1$

$1 + 1+2\vec a.\vec b=1$

$\vec a.\vec b=-\frac{1}{2}$

$|\vec a||\vec b|cos\theta =-\frac{1}{2}$

$cos\theta =-\frac{1}{2}$

$\theta =\frac{2\pi}{3}$

Then $\vec a + \vec b$ is a unit vector if $\theta =\frac{2\pi}{3}$

Hence, option D is correct.

Question:18 The value of $\hat i ( \hat j \times \hat k ) + \hat j ( \hat i \times \hat k ) + \hat k ( \hat i \times \hat j )$ is

(A) 0

(B) –1

(C) 1

(D) 3

Answer:

To find the value of $\hat i ( \hat j \times \hat k ) + \hat j ( \hat i \times \hat k ) + \hat k ( \hat i \times \hat j )$

$\\\hat i ( \hat j \times \hat k ) + \hat j ( \hat i \times \hat k ) + \hat k ( \hat i \times \hat j ) \\=\hat i.\hat i+\hat j(-\hat j)+\hat k.\hat k\\=1-1+1\\=1$

Hence, option C is correct.

Question: 19 Choose the correct. If $\theta$ is the angle between any two vectors $\vec a \: \:and \: \: \vec b$ , then $|\vec a \cdot \vec b |=|\vec a \times \vec b |$ when $\theta$
is equal to

$\\A ) 0 \\\\ B ) \pi /4 \\\\ C ) \pi / 2 \\\\ D ) \pi$

Answer:

Given in the question

$\theta$ is the angle between any two vectors $\vec a \: \:and \: \: \vec b$ and $|\vec a \cdot \vec b |=|\vec a \times \vec b |$

To find the value of $\theta$

Hence, option D is correct.