NCERT Solutions for Miscellaneous Exercise Chapter 11 Class 12

NCERT Solutions for Miscellaneous Exercise Chapter 11 Class 12 - Three Dimensional Geometry

Edited By Ramraj Saini | Updated on Dec 04, 2023 01:50 PM IST | #CBSE Class 12th

Upcoming Event

CBSE Class 12th Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 12 Chapter 11 Miscellaneous Exercise

NCERT Solutions for miscellaneous exercise chapter 11 class 12 Three Dimensional Geometry are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Three Dimensional Geometry is the 11th chapter of NCERT Class 12 Mathematics. The chapter covers a few concepts from lines and planes in three dimensions. Concepts like equations of a line, plane and distance between them etc. A the end of the chapter the miscellaneous exercise comes. Here the NCERT solutions for Class 12 Maths chapter 11 miscellaneous exercise is given. The NCERT book class 12 maths chapter 11 miscellaneous exercise solutions covers questions related to all the concepts of the chapter. These Class 12 Maths chapter 11 miscellaneous solutions are designed by mathematics expert faculties.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

Miscellaneous exercise class 12 chapter 11 are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise enumerated in NCERT Book together using the link provided below.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Three Dimensional Geometry Class 12th Chapter 11-Miscellaneous Exercise

Question:1 Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, – 1), (4, 3, – 1).

Answer:

We can assume the line joining the origin, be OA where $O(0,0,0)$ and the point $A(2,1,1)$ and PQ be the line joining the points $P(3,5,-1)$ and $Q(4,3,-1)$ .

Then the direction ratios of the line OA will be $(2-0),(1-0),\ and\ (1-0) = 2,1,1$ and that of line PQ will be

$(4-3),(3-5),\ and\ (-1+1) = 1,-2,0$

So to check whether line OA is perpendicular to line PQ then,

Applying the relation we know,

$a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

$\Rightarrow 2(1)+1(-2)+1(0) = 2-2+0 = 0$

Therefore OA is perpendicular to line PQ.

Question:2 If l ₁ , m ₁ , n ₁ and l ₂ , m ₂ , n ₂ are the direction cosines of two mutually perpendicular lines, show that the direction cosines of the line perpendicular to both of these are $m_{1}n_{2}-m_{2}n_{1}, n_{1}l_{2}-n_{2}l_{1},l_{1}m_{2}-l_{2}m_{1}$ .

Answer:

Given that $l_1,m_1,n_1\ and\ l_2,m_2,n_2$ are the direction cosines of two mutually perpendicular lines.

Therefore, we have the relation:

$l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2} = 0$ .........................(1)

$l_{1}^2+m_{1}^2+n_{1}^2 =1\ and\ l_{2}^2+m_{2}^2+n_{2}^2 =1$ .............(2)

Now, let us assume $l,m,n$ be the new direction cosines of the lines which are perpendicular to the line with direction cosines. $l_1,m_1,n_1\ and\ l_2,m_2,n_2$

Therefore we have, $ll_{1}+mm_{1}+nn_{1} = 0 \and\ ll_{2}+mm_{2}+nn_{2} = 0$

Or, $\frac{l}{m_{1}n_{2}-m_{2}n_{1}} = \frac{m}{n_{1}l_{2}-n_{2}l_{1}} = \frac{n}{l_{1}m_{2}-l_{2}m_{1}}$

$\Rightarrow \frac{l^2}{(m_{1}n_{2}-m_{2}n_{1})^2} = \frac{m^2}{(n_{1}l_{2}-n_{2}l_{1})^2} = \frac{n^2}{(l_{1}m_{2}-l_{2}m_{1})^2}$

$\Rightarrow \frac{l^2+m^2+n^2}{(m_{1}n_{2}-m_{2}n_{1})^2 +(n_{1}l_{2}-n_{2}l_{1})^2+(l_{1}m_{2}-l_{2}m_{1})^2}$ ......(3)

So, l,m,n are the direction cosines of the line.

where, $l^2+m^2+n^2 =1$ ........................(4)

Then we know that,

$\Rightarrow (l_{1}^2+m_{1}^2+n_{1}^2)(l_{2}^2+m_{2}^2+n_{2}^2) - (l_{1}l_{2}+m_{1}m_{2}+n_{1}n_{2})^2$

$= (m_{1}n_{2}-m_{2}n_{1})^2 + (n_{1}l_{2}-n_{2}l_{1})^2+(l_{1}m_{2}-l_{2}m_{1})^2$

So, from the equation (1) and (2) we have,

$(1)(1) -(0) =(m_{1}n_{2}-m_{2}n_{1})^2 + (n_{1}l_{2}-n_{2}l_{1})^2+(l_{1}m_{2}-l_{2}m_{1})^2$

Therefore, $(m_{1}n_{2}-m_{2}n_{1})^2 + (n_{1}l_{2}-n_{2}l_{1})^2+(l_{1}m_{2}-l_{2}m_{1})^2 =1$ ..(5)

Now, we will substitute the values from the equation (4) and (5) in equation (3), to get

$\frac{l^2}{(m_{1}n_{2}-m_{2}n_{1})^2} = \frac{m^2}{(n_{1}l_{2}-n_{2}l_{1})^2} = \frac{n^2}{(l_{1}m_{2}-l_{2}m_{1})^2} =1$

Therefore we have the direction cosines of the required line as;

$l =m_{1}n_{2} - m_{2}n_{1}$

$m =n_{1}l_{2} - n_{2}l_{1}$

$n =l_{1}m_{2} - l_{2}m_{1}$

Question:3 Find the angle between the lines whose direction ratios are a, b, c and b – c, c – a, a – b.

Answer:

Given direction ratios $a,b,c$ and $b-c,\ c-a,\ a-b$ .

Thus the angle between the lines A is given by;

$A = \left | \frac{a(b-c)+b(c-a)+c(a-b)}{\sqrt{a^2+b^2+c^2}.\sqrt{(b-c)^2+(c-a)^2+(a-b)^2}} \right |$

$\Rightarrow \cos A = 0$

$\Rightarrow A = \cos^{-1}(0) = 90^{\circ}$ a

Thus, the angle between the lines is $90^{\circ}$

Question:4 Find the equation of a line parallel to x-axis and passing through the origin.

Answer:

Equation of a line parallel to the x-axis and passing through the origin $(0,0,0)$ is itself x-axis .

So, let A be a point on the x-axis.

Therefore, the coordinates of A are given by $(a,0,0)$ , where $a\epsilon R$ .

Now, the direction ratios of OA are $(a-0) =a,0 , 0$

So, the equation of OA is given by,

$\frac{x-0}{a} = \frac{y-0}{0} = \frac{z-0}{0}$

or $\Rightarrow \frac{x}{1} = \frac{y}{0} = \frac{z}{0} = a$

Thus, the equation of the line parallel to the x-axis and passing through origin is

$\frac{x}{1} = \frac{y}{0} = \frac{z}{0}$

Question:5 If the coordinates of the points A, B, C, D be (1, 2, 3), (4, 5, 7), (– 4, 3, – 6) and (2, 9, 2) respectively, then find the angle between the lines AB and CD.

Answer:

Direction ratios of AB are $(4-1),(5-2),(7-3) = 3,3,4$

and Direction ratios of CD are $(2-(-4)), (9-3), (2-(-6)) = 6,6,8$

So, it can be noticed that, $\frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} =\frac{c_{1}}{c_{2}} = \frac{1}{2}$

Therefore, AB is parallel to CD.

Thus, we can easily say the angle between AB and CD which is either $0^{\circ}\ or\ 180^{\circ}$ .

Question:6 If the lines $\frac{x-1}{-3}=\frac{y-2}{k}=\frac{z-3}{2}$ and $\frac{x-1}{3k}=\frac{y-1}{1}=\frac{z-6}{-5}$ are perpendicular, find the value of k.

Answer:

Given both lines are perpendicular so we have the relation; $a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2} = 0$

For the two lines whose direction ratios are known,

$a_{1},b_{1},c_{1}\ and\ a_{2},b_{2},c_{2}$

We have the direction ratios of the lines, $\frac{x-1}{-3}=\frac{y-2}{k}=\frac{z-3}{2}$ and $\frac{x-1}{3k}=\frac{y-1}{1}=\frac{z-6}{-5}$ are $-3,2k,2$ and $3k,1,-5$ respectively.

Therefore applying the formula,

$-3(3k)+2k(1)+2(-5) = 0$

$\Rightarrow -9k +2k -10 = 0$

$\Rightarrow7k=-10$ or $k= \frac{-10}{7}$

$\therefore$ For, $k= \frac{-10}{7}$ the lines are perpendicular.

Question:7 Find the vector equation of the line passing through (1, 2, 3) and perpendicular to the plane $\overrightarrow{r}.(\widehat{i}+2\widehat{j}-5\widehat{k})+9=0$

Answer:

Given that the plane is passing through the point $A (1,2,3)$ so, the position vector of the point A is $\vec{r_{A}} = \widehat{i}+2\widehat{j}+3\widehat{k}$ and perpendicular to the plane $\overrightarrow{r}.(\widehat{i}+2\widehat{j}-5\widehat{k})+9=0$ whose direction ratios are $1,2,\ and\ -5$ and the normal vector is $\vec{n} = \widehat{i}+2\widehat{j}-5\widehat{k}$

So, the equation of a line passing through a point and perpendicular to the given plane is given by,

$\vec{l} = \vec{r} + \lambda\vec{n}$ , where $\lambda \epsilon R$

$\Rightarrow \vec{l} = (\widehat{i}+2\widehat{j}+3\widehat{k}) + \lambda(\widehat{i}+2\widehat{j}-5\widehat{k})$

Question:8 Find the equation of the plane passing through (a, b, c) and parallel to the plane $\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=2$ .

Answer:

Given that the plane is passing through $(a,b,c)$ and is parallel to the plane $\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=2$

So, we have

The position vector of the point $A(a,b,c)$ is, $\vec{r_{A}} = a\widehat{i}+b\widehat{j}+c\widehat{k}$

and any plane which is parallel to the plane, $\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=2$ is of the form,

$\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=\lambda$ . .......................(1)

Therefore the equation we get,

$( a\widehat{i}+b\widehat{j}+c\widehat{k}).(\widehat{i}+\widehat{j}+\widehat{k})=\lambda$

Or, $a+b+c = \lambda$

So, now substituting the value of $\lambda = a+b+c$ in equation (1), we get

$\overrightarrow{r}.(\widehat{i}+\widehat{j}+\widehat{k})=a+b+c$ .................(2)

So, this is the required equation of the plane .

Now, substituting $\vec{r} = x\widehat{i}+y\widehat{j}+z\widehat{k}$ in equation (2), we get

$(x\widehat{i}+y\widehat{j}+z\widehat{k}).(\widehat{i}+\widehat{j}+\widehat{k})=a+b+c$

Or, $x+y+z = a+b+c$

Question:9 Find the shortest distance between lines $\overrightarrow{r}=6\widehat{i}+2\widehat{j}+2\widehat{k}+\lambda (\widehat{i}-2\widehat{j}-2\widehat{k})$ and $\overrightarrow{r}=-4\widehat{i}-\widehat{k}+\mu(3\widehat{i}-2\widehat{j}-2\widehat{k})$ .

Answer:

Given lines are;

$\overrightarrow{r}=6\widehat{i}+2\widehat{j}+2\widehat{k}+\lambda (\widehat{i}-2\widehat{j}-2\widehat{k})$ and

$\overrightarrow{r}=-4\widehat{i}-\widehat{k}+\mu(3\widehat{i}-2\widehat{j}-2\widehat{k})$

So, we can find the shortest distance between two lines $\vec{r} = \vec{a_{1}}+\lambda \vec{b_{1}}$ and $\vec{r} = \vec{a_{1}}+\lambda \vec{b_{1}}$ by the formula,

$d = \left | \frac{(\vec{b_{1}}\times\vec{b_{2}}).(\vec{a_{2}}-\vec{a_{1}})}{\left | \vec{b_{1}}\times\vec{b_{2}} \right |} \right |$ ...........................(1)

Now, we have from the comparisons of the given equations of lines.

$\vec{a_{1}} = 6\widehat{i}+2\widehat{j}+2\widehat{k}$ $\vec{b_{1}} = \widehat{i}-2\widehat{j}+2\widehat{k}$

$\vec{a_{2}} = -4\widehat{i}-\widehat{k}$ $\vec{b_{2}} = 3\widehat{i}-2\widehat{j}-2\widehat{k}$

So, $\vec{a_{2}} -\vec{a_{1}} = (-4\widehat{i}-\widehat{k}) -(6\widehat{i}+2\widehat{j}+2\widehat{k}) = -10\widehat{i}-2\widehat{j}-3\widehat{k}$

and $\Rightarrow \vec{b_{1}}\times \vec{b_{2}} = \begin{vmatrix} \widehat{i} &\widehat{j} &\widehat{k} \\ 1 &-2 &2 \\ 3& -2 &-2 \end{vmatrix} = (4+4)\widehat{i}-(-2-6)\widehat{j}+(-2+6)\widehat{k}$

$=8\widehat{i}+8\widehat{j}+4\widehat{k}$

$\therefore \left | \vec{b_{1}}\times \vec{b_{2}} \right | = \sqrt{8^2+8^2+4^2} =12$

$(\vec{b_{1}}\times \vec{b_{2}}).(\vec{a_{2}}-\vec{a_{1}}) = (8\widehat{i}+8\widehat{j}+4\widehat{k}).(-10\widehat{i}-2\widehat{j}-3\widehat{k}) = -80-16-12 =-108$ Now, substituting all values in equation (3) we get,

$d = | \frac{-108}{12}| = 9$

Hence the shortest distance between the two given lines is 9 units.

Question:10 Find the coordinates of the point where the line through (5, 1, 6) and (3, 4,1) crosses the YZ-plane.

Answer:

We know that the equation of the line that passes through the points $(x_{1},y_{1},z_{1})$ and $(x_{2},y_{2},z_{2})$ is given by the relation;

$\frac{x-x_{1}}{x_{2}-x_{1}} = \frac{y-y_{1}}{y_{2}-y_{1}} = \frac{z-z_{1}}{z_{2}-z_{1}}$

and the line passing through the points, $\frac{x-5}{3-5} =\frac{y-1}{4-1} = \frac{z-6}{1-6}$

$\implies \frac{x-5}{-2} = \frac{y-1}{3} = \frac{z-6}{-5} = k\ (say)$

$\implies x=5-2k,\ y=3k+1,\ z=6-5k$

And any point on the line is of the form $(5-2k,3k+1,6-5k)$ .

So, the equation of the YZ plane is $x=0$

Since the line passes through YZ- plane,

we have then,

$5-2k = 0$

$\Rightarrow k =\frac{5}{2}$

or $3k+1 = 3(\frac{5}{2})+1 = \frac{17}{2}$ and $6-5k= 6-5(\frac{5}{2}) = \frac{-13}{2}$

So, therefore the required point is $\left ( 0,\frac{17}{2},\frac{-13}{2} \right )$

Question : 11 Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the ZX-plane.

Answer:

We know that the equation of the line that passes through the points $(x_{1},y_{1},z_{1})$ and $(x_{2},y_{2},z_{2})$ is given by the relation;

$\frac{x-x_{1}}{x_{2}-x_{1}} = \frac{y-y_{1}}{y_{2}-y_{1}} = \frac{z-z_{1}}{z_{2}-z_{1}}$

and the line passing through the points, $\frac{x-5}{3-5} =\frac{y-1}{4-1} = \frac{z-6}{1-6}$

$\implies \frac{x-5}{-2} = \frac{y-1}{3} = \frac{z-6}{-5} = k\ (say)$

$\implies x=5-2k,\ y=3k+1,\ z=6-5k$

And any point on the line is of the form $(5-2k,3k+1,6-5k)$ .

So, the equation of ZX plane is $y=0$

Since the line passes through YZ- plane,

we have then,

$3k+1 = 0$

$\Rightarrow k =-\frac{1}{3}$

or $5-2k = 5-2\left ( -\frac{1}{3} \right ) = \frac{17}{3}$ and $6-5k= 6-5(\frac{-1}{3}) = \frac{23}{3}$

So, therefore the required point is $\left ( \frac{17}{3},0,\frac{23}{3} \right )$

Question:12 Find the coordinates of the point where the line through (3, – 4, – 5) and (2, – 3, 1) crosses the plane 2x + y + z = 7.

Answer:

We know that the equation of the line that passes through the points $(x_{1},y_{1},z_{1})$ and $(x_{2},y_{2},z_{2})$ is given by the relation;

$\frac{x-x_{1}}{x_{2}-x_{1}} = \frac{y-y_{1}}{y_{2}-y_{1}} = \frac{z-z_{1}}{z_{2}-z_{1}}$

and the line passing through the points, $(3,-4,-5)\ and\ (2,-3,1)$ .

$\implies \frac{x-3}{2-3} = \frac{y+4}{-3+4} = \frac{z+5}{1+5} = k\ (say)$

$\implies \frac{x-3}{-1} = \frac{y+4}{-1} = \frac{z+5}{6} = k\ (say)$

$\implies x=3-k,\ y=k-4,\ z=6k-5$

And any point on the line is of the form. $(3-k,k-4,6k-5)$

This point lies on the plane, $2x+y+z = 7$

$\therefore 2(3-k)+(k-4)+(6k-5) = 7$

$\implies 5k-3=7$

or $k =2$ .

Hence, the coordinates of the required point are $(3-2,2-4,6(2)-5)$ or $(1,-2,7)$ .

Question:13 Find the equation of the plane passing through the point (– 1, 3, 2) and perpendicular to each of the planes x + 2y + 3z = 5 and 3x + 3y + z = 0.

Answer:

Given

two planes x + 2y + 3z = 5 and 3x + 3y + z = 0.

the normal vectors of these plane are

$n_1=\hat i+2\hat j+ 3\hat k$

$n_2=3\hat i+3\hat j+ \hat k$

Since the normal vector of the required plane is perpendicular to the normal vector of given planes, the required plane's normal vector will be :

$\vec n = \vec n_1\times\vec n_2$

$\vec n = (\hat i+2\hat j +3\hat k )\times (3\hat i + 3\hat j +\hat k)$

$\vec n =\begin{vmatrix} \hat i &\hat j &\hat k \\ 1 &2 &3 \\ 3& 3& 1 \end{vmatrix}=\hat i(2-9)-\hat j(1-9)+\hat k (3-6)$

$\vec n =-7\hat i+8\hat j-3\hat k$

Now, as we know

the equation of a plane in vector form is :

$\vec r\cdot\vec n=d$

$\vec r\cdot(-7\hat i+8\hat j-3\hat k)=d$

Now Since this plane passes through the point (-1,3,2)

$(-\hat i+3\hat j+2\hat k)\cdot(-7\hat i+8\hat j-3\hat k)=d$

$7+24-6=d$

$d=25$

Hence the equation of the plane is

$\vec r\cdot(-7\hat i+8\hat j-3\hat k)=25$

Question:14 If the points (1, 1, p) and (– 3, 0, 1) be equidistant from the plane $\overrightarrow{r}.(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 =0$ then find the value of p.

Answer:

Given that the points $A(1,1,p)$ and $B(-3,0,1)$ are equidistant from the plane

$\overrightarrow{r}.(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 =0$

So we can write the position vector through the point $(1,1,p)$ is $\vec{a_{1}} = \widehat{i}+\widehat{j}+p\widehat{k}$

Similarly, the position vector through the point $B(-3,0,1)$ is

$\vec{a_{2}} = -4\widehat{i}+\widehat{k}$

The equation of the given plane is $\overrightarrow{r}.(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 =0$

and We know that the perpendicular distance between a point whose position vector is $\vec{a}$ and the plane, $\vec{n} = 3\widehat{i}+4\widehat{j}-12\widehat{k}$ and $d =-13$

Therefore, the distance between the point $A(1,1,p)$ and the given plane is

$D_{1} = \frac{\left | (\widehat{i}+\widehat{j}+p\widehat{k}).(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 \right |}{3\widehat{i}+4\widehat{j}-12\widehat{k}}$

$D_{1} = \frac{\left | 3+4-12p+13 \right |}{\sqrt{3^2+4^2+(-12)^2}}$

$D_{1} = \frac{\left | 20-12p \right |}{13}$ nbsp; .........................(1)

Similarly, the distance between the point $B(-1,0,1)$ , and the given plane is

$D_{2} = \frac{\left | (-3\widehat{i}+\widehat{k}).(3\widehat{i}+4\widehat{j}-12\widehat{k})+13 \right |}{3\widehat{i}+4\widehat{j}-12\widehat{k}}$

$D_{2} = \frac{\left |-9-12+13 \right |}{\sqrt{3^2+4^2+(-12)^2}}$

$D_{2} = \frac{8}{13}$ .........................(2)

And it is given that the distance between the required plane and the points, $A(1,1,p)$ and $B(-3,0,1)$ is equal.

$\therefore D_{1} =D_{2}$

$\implies \frac{\left | 20-12p \right |}{13} =\frac{8}{13}$

therefore we have,

$\implies 12p =12$

or $p =1$ or $p = \frac{7}{3}$

Question:15 Find the equation of the plane passing through the line of intersection of the planes $\overrightarrow{r}.\left ( \widehat{i}+\widehat{j}+\widehat{k} \right )=1$ and $\overrightarrow{r}.\left (2 \widehat{i}+3\widehat{j}-\widehat{k} \right )+4=0$ and parallel to x-axis.

Answer:

So, the given planes are:

$\overrightarrow{r}.\left ( \widehat{i}+\widehat{j}+\widehat{k} \right )=1$ and $\overrightarrow{r}.\left (2 \widehat{i}+3\widehat{j}-\widehat{k} \right )+4=0$

The equation of any plane passing through the line of intersection of these planes is

$[\overrightarrow{r}.\left ( \widehat{i}+\widehat{j}+\widehat{k} \right )-1] + \lambda \left [ \overrightarrow{r}.\left (2 \widehat{i}+3\widehat{j}-\widehat{k} \right )+4\right ] = 0$

$\vec{r}.[(2\lambda+1)\widehat{i}+(3\lambda+1)\widehat{j}+(1-\lambda)\widehat{k}]+(4\lambda+1) = 0$ ..............(1)

Its direction ratios are $(2\lambda+1) , (3\lambda+1),$ and $(1-\lambda)$ = 0

The required plane is parallel to the x-axis.

Therefore, its normal is perpendicular to the x-axis.

The direction ratios of the x-axis are 1,0, and 0.

$\therefore \1.(2\lambda+1) + 0(\3\lambda+1)+0(1-\lambda) = 0$

$\implies 2\lambda+1 = 0$

$\implies \lambda = -\frac{1}{2}$

Substituting $\lambda = -\frac{1}{2}$ in equation (1), we obtain

$\implies \vec{r}.\left [ -\frac{1}{2}\widehat{j}+\frac{3}{2}\widehat{k} \right ]+(-3)= 0$

$\implies \vec{r}(\widehat{j}-3\widehat{k})+6= 0$

So, the Cartesian equation is $y -3z+6 = 0$

Question:16 If O be the origin and the coordinates of P be (1, 2, – 3), then find the equation of the plane passing through P and perpendicular to OP.

Answer:

We have the coordinates of the points $O(0,0,0)$ and $P(1,2,-3)$ respectively.

Therefore, the direction ratios of OP are $(1-0) = 1, (2-0)=2,\ and\ (-3-0)=-3$

And we know that the equation of the plane passing through the point $(x_{1},y_{1},z_{1})$ is

$a(x-x_{1})+b(y-y_{1})+c(z-z_{1})=0$ where a,b,c are the direction ratios of normal.

Here, the direction ratios of normal are $1,2,$ and $-3$ and the point P is $(1,2,-3)$ .

Thus, the equation of the required plane is

$1(x-1)+2(y-2)-3(z+3) = 0$

$\implies x+2y -3z-14 = 0$

Question:17 Find the equation of the plane which contains the line of intersection of the planes $\overrightarrow{r}.(\widehat{i}+2\widehat{j}+3\widehat{k})-4=0,\overrightarrow{r}.\left ( 2\widehat{i}+\widehat{j}-\widehat{k} \right )+5=0$ and which is perpendicular to the plane $\overrightarrow{r}.(5\widehat{i}+3\widehat{j}-6\widehat{k})+8=0$

Answer:

The equation of the plane passing through the line of intersection of the given plane in $\overrightarrow{r}.(\widehat{i}+2\widehat{j}+3\widehat{k})-4=0,\overrightarrow{r}.\left ( 2\widehat{i}+\widehat{j}-\widehat{k} \right )+5=0$

$\left [ \vec{r}.(\widehat{i}+2\widehat{j}+3\widehat{k})-4 \right ]+\lambda\left [ \vec{r}.\left ( 2\widehat{i}+\widehat{j}-\widehat{k} \right )+5 \right ] = 0$

$\vec{r}.[(2\lambda+1)\widehat{i}+(\lambda+2)\widehat{j}+(3-\lambda)\widehat{k}]+(5\lambda-4)= 0$ ,,,,,,,,,,,,,(1)

The plane in equation (1) is perpendicular to the plane, 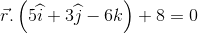1633928330199 Therefore $5(2\lambda+1)+3(\lambda+2) -6(3-\lambda) = 0$

$\implies 19\lambda -7 = 0$

$\implies \lambda = \frac{7}{19}$

Substituting $\lambda = \frac{7}{19}$ in equation (1), we obtain

$\implies \vec{r}.\left [ \frac{33}{19}\widehat{i}+\frac{45}{19}\widehat{j}+\frac{50}{19}\widehat{k} \right ] -\frac{41}{19} = 0$

$\implies \vec{r}.(33\widehat{i}+45\widehat{j}+50\widehat{k}) -41 = 0$ .......................(4)

So, this is the vector equation of the required plane.

The Cartesian equation of this plane can be obtained by substituting $\implies \vec{r}= (x\widehat{i}+y\widehat{j}+z\widehat{k})$ in equation (1).

$(x\widehat{i}+y\widehat{j}+z\widehat{k}).(33\widehat{i}+45\widehat{j}+50\widehat{k}) -41 = 0$

Therefore we get the answer $33x+45y+50z -41 = 0$

Question:18 Find the distance of the point (– 1, – 5, – 10) from the point of intersection of the line $\overrightarrow{r}=2\widehat{i}-\widehat{j}+2\widehat{k}+ \lambda\left ( 3\widehat{i}+4\widehat{j}+2\widehat{k} \right )$ and the plane $\overrightarrow{r}.\left ( \widehat{i}-\widehat{j}+\widehat{k} \right )=5$ .

Answer:

Given,

Equation of a line :

$\overrightarrow{r}=2\widehat{i}-\widehat{j}+2\widehat{k}+ \lambda\left ( 3\widehat{i}+4\widehat{j}+2\widehat{k} \right )$

Equation of the plane

$\overrightarrow{r}.\left ( \widehat{i}-\widehat{j}+\widehat{k} \right )=5$

Let's first find out the point of intersection of line and plane.

putting the value of $\vec r$ into the equation of a plane from the equation from line

$\left (2\widehat{i}-\widehat{j}+2\widehat{k}+ \lambda\left ( 3\widehat{i}+4\widehat{j}+2\widehat{k} \right ) \right )\cdot (\hat i-\hat j+\hat k)=5$

$(2+3\lambda)-(4\lambda -1)+(2+2\lambda)=5$

$\lambda+5=5$

$\lambda=0$

Now, from the equation, any point p in line is

$P=(2+3\lambda,4\lambda-1,2+2\lambda)$

So the point of intersection is

$P=(2+3*0,4*0-1,2+2*0)=(2,-1,2)$

SO, Now,

The distance between the points (-1,-5,-10) and (2,-1,2) is

$d=\sqrt{(2-(-1))^2+(-1-(-5))^2+(2-(-10))^2}=\sqrt{9+16+144}$

$d=\sqrt{169}=13$

Hence the required distance is 13.

Question:19 Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes $\overrightarrow{r}.\left ( \widehat{i}-\widehat{j}+2\widehat{k} \right )=5$ and $\overrightarrow{r}.\left ( 3\widehat{i}+\widehat{j}+\widehat{k} \right )=6$ .

Answer:

Given

A point through which line passes

$\vec a=\hat i+2\hat j+3\hat k$

two plane

$\overrightarrow{r}.\left ( \widehat{i}-\widehat{j}+2\widehat{k} \right )=5$ And

$\overrightarrow{r}.\left ( 3\widehat{i}+\widehat{j}+\widehat{k} \right )=6$

it can be seen that normals of the planes are

$\vec n_1=\hat i-\hat j+2\hat k$

$\vec n_2=3\hat i+\hat j+\hat k$
since the line is parallel to both planes, its parallel vector will be perpendicular to normals of both planes.

So, a vector perpendicular to both these normal vector is

$\vec d=\vec n_1\times\vec n_2$

$\vec d=\begin{vmatrix} \hat i &\hat j & \hat k\\ 1 &-1 &2 \\ 3& 1 & 1 \end{vmatrix}=\hat i(-1-2)-\hat j(1-6)+\hat k(1+3)$

$\vec d=-3\hat i+5\hat j+4\hat k$

Now a line which passes through $\vec a$ and parallels to $\vec d$ is

$L=\vec a+\lambda\vec d$

So the required line is

$L=\vec a+\lambda\vec d$

$L=\hat i+2\hat j+3\hat k+\lambda(-3\hat i+5\hat j+4\hat k)$

$L=(1-3\lambda)\hat i+(2+5\lambda)\hat j+(3+4\lambda)\hat k$

Questio n: 20 Find the vector equation of the line passing through the point (1, 2, – 4) and perpendicular to the two lines:

$\frac{x-8}{3}=\frac{y+19}{-16}=\frac{z-10}{7}$ and $\frac{x-15}{3}=\frac{y-29}{8}=\frac{z-5}{-5}$

Answer:

Given

Two straight lines in 3D whose direction cosines (3,-16,7) and (3,8,-5)

Now the two vectors which are parallel to the two lines are

$\vec a= 3\hat i-16\hat j+7\hat k$ and

$\vec b= 3\hat i+8\hat j-5\hat k$

As we know, a vector perpendicular to both vectors $\vec a$ and $\vec b$ is $\vec a\times\vec b$ , so

$\vec a\times\vec b=\begin{vmatrix} \hat i &\hat j &\hat k \\ 3& -16 &7 \\ 3&8 &-5 \end{vmatrix}=\hat i(80-56)-\hat j(-15-21)+\hat k(24+48)$

$\vec a\times\vec b=24\hat i+36\hat j+72\hat k$

A vector parallel to this vector is

$\vec d=2\hat i+3\hat j+6\hat k$

Now as we know the vector equation of the line which passes through point p and parallel to vector d is

$L=\vec p+\lambda \vec d$

Here in our question, give point p = (1,2,-4) which means position vector of this point is

$\vec p = \hat i +2\hat j-4\hat k$

So, the required line is

$L=\vec p+\lambda \vec d$

$L=\hat i+2\hat j-4\hat k +\lambda (2\hat i+3\hat j+6\hat k)$

$L=(2\lambda +1)\hat i+(2+3\lambda)\hat j+(6\lambda-4)\hat k$

Question:21 Prove that if a plane has the intercepts a, b, c and is at a distance of p units from the origin, then $\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}=\frac{1}{p^{2}}$ .

Answer:

The equation of plane having a, b and c intercepts with x, y and z-axis respectively is given by
$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}= 1$
The distance p of the plane from the origin is given by
$\\p = \left | \frac{\frac{0}{a}+\frac{0}{b}+\frac{0}{c}-1}{\sqrt{(\frac{1}{a})^2+(\frac{1}{b})^2(\frac{1}{c})^2}} \right |\\ \\ p = \left | \frac{-1}{\sqrt{(\frac{1}{a})^2+(\frac{1}{b})^2(\frac{1}{c})^2}} \right |\\ \\ \frac{1}{p^2}= \frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}$
Hence proved

Question:22 Distance between the two planes: 2x + 3y + 4z = 4 and 4x + 6y + 8z = 12 is

(A) 2 units (B) 4 units (C) 8 units (D) $\frac{2}{\sqrt{29}}unit$

Answer:

Given equations are
$2x+3y+4z= 4 \ \ \ \ \ \ \ \ \ -(i)$
and
$4x+6y+8z= 12\\ 2(2x+3y+4z)= 12\\ 2x+3y+4z = 6 \ \ \ \ \ \ \ \ \ \ -(ii)$
Now, it is clear from equation (i) and (ii) that given planes are parallel
We know that the distance between two parallel planes $ax+by +cz = d_1 \ and \ ax+by +cz = d_2$ is given by
$D= \left | \frac{d_2-d_1}{\sqrt{a^2+b^2+c^2}} \right |$
Put the values in this equation
we will get,
$D= \left | \frac{6-4}{\sqrt{2^2+3^2+4^2}} \right |$
$D= \left | \frac{2}{\sqrt{4+9+16}} \right |= \left | \frac{2}{\sqrt{29}} \right |$
Therefore, the correct answer is (D)

Question:23 The planes: 2x – y + 4z = 5 and 5x – 2.5y + 10z = 6 are

(A) Perpendicular (B) Parallel (C) intersect y-axis (D) passes through $\left ( 0,0,\frac{5}{4} \right )$

Answer:

Given equations of planes are
$2x-y+4z=5 \ \ \ \ \ \ \ \ \ -(i)$
and
$5x-2.5y+10z=6\\ 2.5(2x-y+4z)=6\\ 2x-y+4z= 2.4 \ \ \ \ \ \ \ \ \ -(ii)$
Now, from equation (i) and (ii) it is clear that given planes are parallel to each other
$\because \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\Rightarrow \frac{2}{2}= \frac{-1}{-1}=\frac{4}{4}\Rightarrow 1=1=1$
Therefore, the correct answer is (B)

Benefits of NCERT Solutions for Class 12 Maths Chapter 11 Miscellaneous Exercise

To practise the complete chapter the miscellaneous exercise chapter 11 Class 12 is useful
To practice for the board exam the NCERT solutions for Class 12 Maths chapter 11 miscellaneous exercise is helpful.

JEE Main Highest Scoring Chapters & Topics

Just Study 40% Syllabus and Score upto 100%

Download EBook

Key Features Of NCERT Solutions For Class 12 Chapter 11 Miscellaneous Exercise

Comprehensive Coverage: The solutions encompass all the topics covered in miscellaneous exercise class 12 chapter 11, ensuring a thorough understanding of the concepts.
Step-by-Step Solutions: In this class 12 chapter 11 maths miscellaneous solutions, each problem is solved systematically, providing a stepwise approach to aid in better comprehension for students.
Accuracy and Clarity: Solutions for class 12 maths miscellaneous exercise chapter 11 are presented accurately and concisely, using simple language to help students grasp the concepts easily.
Conceptual Clarity: In this class 12 maths ch 11 miscellaneous exercise solutions, emphasis is placed on conceptual clarity, providing explanations that assist students in understanding the underlying principles behind each problem.
Inclusive Approach: Solutions for class 12 chapter 11 miscellaneous exercise cater to different learning styles and abilities, ensuring that students of various levels can grasp the concepts effectively.
Relevance to Curriculum: The solutions for miscellaneous exercise class 12 chapter 11 align closely with the NCERT curriculum, ensuring that students are prepared in line with the prescribed syllabus.

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. How many exercises are covered in the NCERT Class 12 chapter 3 dimensional geometry?

Total four exercises are covered in three-dimensional geometry.

2. Give a difference between one, two and three dimensions?

One dimension is represented by a single axis (say x-axis), in two dimensions we have two axes (say x and y-axis) and three-dimension in space is is represented by three axes (say x,y and z-axis)

3. How many questions are solved in the NCERT solutions for Class 12 Maths chapter 11 miscellaneous exercise?

23 questions are solved in the miscellaneous exercise of class 12 chapter

4. How many exercises are solved before miscellaneous?

Three exercises are solved before miscellaneous exercise of Cass 12 Maths chapter three dimensional geometry

5. What is the importance of the NCERT syllabus?

NCERT syllabus is required for the preparation of CBSE board exams and some of the state board exams like Kerala state board. Also, NCERT is considered as the bible for the preparation of NEET exams (physics, chemistry and biology). Also, the NCERT syllabus is helpful for JEE main exam (Physics, Chemistry and Mathematics)

6. Why do we solve NCERT Class 12 chapter 11 exercises?

To practice the concepts covered in the chapter.

7. What is the importance of miscellaneous exercises?

Miscellaneous exercises give a good variety of problems covering the entire chapter.

8. Can we expect questions from miscellaneous exercises for board exams?

Yes, sometimes the type of questions discussed in miscellaneous exercises are asked for both board exams and competitive exams as well.

Also Read

NCERT Class 12 Maths Notes - Download Chapter wise Free PDFs

NCERT Class 12 Physics Chapter 9 Notes Ray Optics and Optical Instruments - Download PDF

NCERT Class 12 Physics Chapter 8 Notes Electromagnetic Waves - Download PDF

NCERT Class 12 Physics Chapter 7 Notes Alternating Current - Download PDF

NCERT Class 12 Physics Chapter 6 Notes Electromagnetic Induction - Download PDF

NCERT Class 12 Physics Chapter 5 Notes Magnetism and Matter - Download PDF

NCERT Books for Class 12 - Download All Subjects PDFs Here

NCERT Solutions for Miscellaneous Exercise Chapter 7 Class 12 - Integrals

NCERT Solutions for Exercise 4.1 Class 11 Maths Chapter 4 - Principle of Mathematical Induction

NCERT Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

NCERT Exemplar Class 12 Physics Solutions Chapter 8 Electromagnetic Waves

Articles

APOSS Inter Time Table 2025 - Check Andhra Pradesh Open School Exam Dates

Dec 19, 2024

CBSE Class 11 Date Sheet 2025 – Download Class 11th Exam Schedule for All Subjects

Dec 19, 2024

CBSE Class 12 Maths Syllabus 2024-25: Download PDF

Dec 19, 2024

UP Board Practical Exams 2025 - UPMSP High School and Inter Viva to Be Recorded to Ensure Transparency

Dec 19, 2024

JAC 12th Result 2024 Commerce OUT, Check Jharkhand 12th Commerce Result @jacresults.com

Dec 19, 2024

CBSE Class 12 English 2025: Expected Article Writing Questions to Prepare

Dec 17, 2024

Score Above 90% in CBSE Class 12 Board Exam 2025: 2-month Preparation Plan

Dec 17, 2024

CBSE Exam Rules for Class 10 and 12: New Guidelines For CBSE Exams 2024-25

Dec 13, 2024

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

Admit Card

Result

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Eligibility Criteria

Application Process

Exam Pattern

Madhya Pradesh State Open School 12th Examination

Admit Card Date:13 December,2024 - 06 January,2025

Admit Card

Result

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Exam Pattern

Result

Admit Card

View All School Exams

Certifications By Top Providers

My SQL Basics

Via Great Learning

Full-Stack Web Development

Via Masai School

Business Analytics Foundations

Via PW Skills

Digital Banking Business Model

Via State Bank of India

Full-Stack Android Development

Via Masai School

Machine Learning with Python a Practical Introduction

Via IBM

1115 courses

816 courses

394 courses

295 courses

Harvard University, Cambridge

98 courses

University of Michigan, Ann Arbor

83 courses

IT & Software

Teaching and Academics

Programming and Development

Health, Fitness and Medicine

Business and Management

Engineering and Architecture

General Management

Financial Management

Environmental Studies

History

Psychology

Artificial Intelligence

Explore Top Universities Across Globe

University of Essex, Colchester

Wivenhoe Park Colchester CO4 3SQ

University College London, London

Gower Street, London, WC1E 6BT

The University of Edinburgh, Edinburgh

Old College, South Bridge, Edinburgh, Post Code EH8 9YL

University of Bristol, Bristol

Beacon House, Queens Road, Bristol, BS8 1QU

University of Delaware, Newark

Newark, DE 19716

University of Nottingham, Nottingham

University Park, Nottingham NG7 2RD

Exams Required to Study in USA: GMAT, GRE, SAT, ACT, IELTS, PTE

9 min ⋆ Dec 19, 2024 06:12 AM IST

Countries Tightened Visa Rules for International Students in 2025

9 min ⋆ Dec 19, 2024 06:12 AM IST

PR in France for Indian and International Students 2025

11 min ⋆ Dec 19, 2024 05:12 AM IST

PR in USA for Indian Students in 2025

8 min ⋆ Dec 19, 2024 05:12 AM IST

Cheapest and Affordable Universities in France for International Students in 2025

12 min ⋆ Dec 19, 2024 05:12 AM IST

Study in Singapore for Indian Students in 2025

12 min ⋆ Dec 19, 2024 05:12 AM IST

Related E-books & Sample Papers

CBSE Class 12 Accountancy Question Papers 2024 (Code-PQ1RS/1) – All Sets (1, 2, 3)

35+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-QSS4R/4) – All Sets (1, 2, 3)

40+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-Q5QPS/5) – All Sets (1, 2, 3)

17+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code- PQ3RS/3) – All Sets (1, 2, 3)

6+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-PQ2RS/2) – All Sets (1, 2, 3)

5+ Downloads

CBSE Class 12 Maths Question Papers 2024 (Code-PQ1RS/1) – All Sets (1, 2, 3)

6+ Downloads

Questions related to CBSE Class 12th

Have a question related to CBSE Class 12th ?

quartely question paper for mathematics cbse

Hello there! Thanks for reaching out to us at Careers360.

Ah, you're looking for CBSE quarterly question papers for mathematics, right? Those can be super helpful for exam prep.

Unfortunately, CBSE doesn't officially release quarterly papers - they mainly put out sample papers and previous years' board exam papers. But don't worry, there are still some good options to help you practice!

Have you checked out the CBSE sample papers on their official website? Those are usually pretty close to the actual exam format. You could also look into previous years' board exam papers - they're great for getting a feel for the types of questions that might come up.

If you're after more practice material, some textbook publishers release their own mock papers which can be useful too.

Let me know if you need any other tips for your math prep. Good luck with your studies!

Read Complete Answer

Jefferson 25 September,2024

i have taken admission in clg after my campartment exam in chemistry along with the neet 2025 preperation but unfortunately i again got campartment after doing all this preparation i got 15 marks only now I can't able to think what should I do next.

It's understandable to feel disheartened after facing a compartment exam, especially when you've invested significant effort. However, it's important to remember that setbacks are a part of life, and they can be opportunities for growth.

Possible steps:

Re-evaluate Your Study Strategies:
- Identify Weak Areas: Pinpoint the specific topics or concepts that caused difficulties.
- Seek Clarification: Reach out to teachers, tutors, or online resources for additional explanations.
- Practice Regularly: Consistent practice is key to mastering chemistry.
Consider Professional Help:
- Tutoring: A tutor can provide personalized guidance and support.
- Counseling: If you're feeling overwhelmed or unsure about your path, counseling can help.
Explore Alternative Options:
- Retake the Exam: If you're confident in your ability to improve, consider retaking the chemistry compartment exam.
- Change Course: If you're not interested in pursuing chemistry further, explore other academic options that align with your interests.
Focus on NEET 2025 Preparation:
- Stay Dedicated: Continue your NEET preparation with renewed determination.
- Utilize Resources: Make use of study materials, online courses, and mock tests.
Seek Support:
- Talk to Friends and Family: Sharing your feelings can provide comfort and encouragement.
- Join Study Groups: Collaborating with peers can create a supportive learning environment.

Remember: This is a temporary setback. With the right approach and perseverance, you can overcome this challenge and achieve your goals.

I hope this information helps you.

Read Complete Answer

Kanishka kaushikii 17 September,2024

i scored 84 percent in cbse 2 years ago.Am i eligible for medhavi scholarship if give 12th again after 2 drop years and will got 75+ in mpboard

Hi,

Qualifications:
Age: As of the last registration date, you must be between the ages of 16 and 40.
Qualification: You must have graduated from an accredited board or at least passed the tenth grade. Higher qualifications are also accepted, such as a diploma, postgraduate degree, graduation, or 11th or 12th grade.
How to Apply:
Get the Medhavi app by visiting the Google Play Store.
Register: In the app, create an account.
Examine Notification: Examine the comprehensive notification on the scholarship examination.
Sign up to Take the Test: Finish the app's registration process.
Examine: The Medhavi app allows you to take the exam from the comfort of your home.
Get Results: In just two days, the results are made public.
Verification of Documents: Provide the required paperwork and bank account information for validation.
Get Scholarship: Following a successful verification process, the scholarship will be given. You need to have at least passed the 10th grade/matriculation scholarship amount will be transferred directly to your bank account.

Scholarship Details:

Type A: For candidates scoring 60% or above in the exam.

Type B: For candidates scoring between 50% and 60%.

Type C: For candidates scoring between 40% and 50%.

Cash Scholarship:

Scholarships can range from Rs. 2,000 to Rs. 18,000 per month, depending on the marks obtained and the type of scholarship exam (SAKSHAM, SWABHIMAN, SAMADHAN, etc.).

Since you already have a 12th grade qualification with 84%, you meet the qualification criteria and are eligible to apply for the Medhavi Scholarship exam. Make sure to prepare well for the exam to maximize your chances of receiving a higher scholarship.

Hope you find this useful!

Read Complete Answer

Yuvan 30 August,2024

i upload 12th board result screenshot in ncweb form from the cbse site so it is valid

hello mahima,

If you have uploaded screenshot of your 12th board result taken from CBSE official website,there won,t be a problem with that.If the screenshot that you have uploaded is clear and legible. It should display your name, roll number, marks obtained, and any other relevant details in a readable forma.ALSO, the screenshot clearly show it is from the official CBSE results portal.

hope this helps.

Read Complete Answer

Ashvadha 12 July,2024

Kya mujhe class 12 ka important question milega jo exam mai per year puche jate hai

Hello Akash,

If you are looking for important questions of class 12th then I would like to suggest you to go with previous year questions of that particular board. You can go with last 5-10 years of PYQs so and after going through all the questions you will have a clear idea about the type and level of questions that are being asked and it will help you to boost your class 12th board preparation.

You can get the Previous Year Questions (PYQs) on the official website of the respective board.

I hope this answer helps you. If you have more queries then feel free to share your questions with us we will be happy to assist you.

Thank you and wishing you all the best for your bright future.

Read Complete Answer

kumardurgesh1802 10 July,2024

View All

Stay up-to date with CBSE Class 12th News

Download Careers360 App

All this at the convenience of your phone

Regular Exam Updates
Best College Recommendations
College & Rank predictors
Detailed Books and Sample Papers
Question and Answers

Scan and download the app

Central Board of Secondary Education Class 12th Examination

JEE Test Series

Applications Open

Option 1) $0.34\; J$	Option 2) $0.16\; J$
Option 3) $1.00\; J$	Option 4) $0.67\; J$

Option 1) $2,000 \; J - 5,000\; J$	Option 2) $200 \, \, J - 500 \, \, J$
Option 3) $2\times 10^{5}J-3\times 10^{5}J$	Option 4) $20,000 \, \, J - 50,000 \, \, J$

Option 1) $K/2\,$	Option 2) $\; K\;$
Option 3) $zero\;$	Option 4) $K/4$

Option 1) $11.2\, L\, H_{2(g)}$ at STP is produced for every mole $HCL_{(aq)}$ consumed	Option 2) $6L\, HCl_{(aq)}$ is consumed for ever $3L\, H_{2(g)}$ produced
Option 3) $33.6 L\, H_{2(g)}$ is produced regardless of temperature and pressure for every mole Al that reacts	Option 4) $67.2\, L\, H_{2(g)}$ at STP is produced for every mole Al that reacts .

Option 1) 0.02	Option 2) 3.125 × 10^-2
Option 3) 1.25 × 10^-2	Option 4) 2.5 × 10^-2

Option 1) decrease twice	Option 2) increase two fold
Option 3) remain unchanged	Option 4) be a function of the molecular mass of the substance.

Option 1) Molality	Option 2) Weight fraction of solute
Option 3) Fraction of solute present in water	Option 4) Mole fraction.

Option 1) twice that in 60 g carbon	Option 2) 6.023 × 10²²
Option 3) half that in 8 g He	Option 4) 558.5 × 6.023 × 10²³

Option 1) less than 3	Option 2) more than 3 but less than 6
Option 3) more than 6 but less than 9	Option 4) more than 9

NCERT Solutions for Miscellaneous Exercise Chapter 11 Class 12 - Three Dimensional Geometry

NCERT Solutions For Class 12 Chapter 11 Miscellaneous Exercise

Pearson | PTE

Three Dimensional Geometry Class 12th Chapter 11-Miscellaneous Exercise

More About NCERT Solutions for Class 12 Maths Chapter 11 Miscellaneous Exercise

Benefits of NCERT Solutions for Class 12 Maths Chapter 11 Miscellaneous Exercise

Key Features Of NCERT Solutions For Class 12 Chapter 11 Miscellaneous Exercise

Also see-

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

Also Read

Articles

Upcoming School Exams

Certifications By Top Providers

Explore Top Universities Across Globe

Related E-books & Sample Papers

Questions related to CBSE Class 12th

Popular CBSE Class 12th Questions

Colleges After 12th

JEE Main Important Physics formulas

JEE Main Important Chemistry formulas

TOEFL ® Registrations 2024

Pearson | PTE

JEE Main high scoring chapters and topics

JEE Main Important Mathematics Formulas

Stay up-to date with CBSE Class 12th News

Explore on Careers360

NCERT Solutions

NCERT Exemplars

NCERT Books

NCERT Notes

CBSE

CBSE Class 10

CBSE Class 12th

CISCE Board 10th

IMO

IEO

NSO

NMMS

NVS

JNVST

Schools By Medium

By Ownership

By City

By State

Download Careers360 App

All this at the convenience of your phone

Scan and download the app