• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations

Edited By Saumya.Srivastava | Updated on Sep 05, 2023 07:24 PM IST

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations

Here students will get NCERT Solutions For Quadratic Equation class 10 which are created by expert team at Careers360 keeping in mind of latest syllabus of CBSE 2023-24. These solutions are very helpful for students to understand the basic concepts in a better way as these cover all the topics mentioned in syllabus comprehensive also include step by step explanation of each problem. When we equate the quadratic polynomial to zero, then we get a quadratic equation. NCERT Solutions for Class 10 Maths will help students to get indept understanding of the concepts and thus help students to strategise their preparation. They must complete the NCERT Class 10 Maths syllabus to the earliest so that they can revise in a strategic way. Each exercises of Quadratic Equation Class 10 are solved here in detailled manner.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations
  2. NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations PDF Free Download
  3. NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations - Important Formulae
  4. NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations (Intext Questions and Exercise)
  5. Topics of Class 10 Maths Chapter 4 Quadratic Equations
  6. NCERT Books and NCERT Syllabus
  7. Key Features For Chapter 4 Maths Class 10
  8. NCERT solutions for class 10 Maths - Chapter Wise
NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations
NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations

Understanding quadratic equations chapter 4 maths class 10 is crucial as they appear in various real-life scenarios. Students must focus on mastering this chapter in the 2023-24 CBSE Syllabus to excel in Class 10 Math exams. NCERT solutions are valuable tools for comprehension and self-assessment. Regular practice with these solutions aids in addressing weaknesses. In mathematics, answers are either right or wrong, making concentration essential for achieving full marks.

Also read :

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations PDF Free Download

Download PDF

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations - Important Formulae

Quadratic Equation:

f(x) = ax2 + bx + c, Where a, b, c ∈ R and a ≠ 0.

Quadratic Formula - Roots:

  • (α, β) = [-b ± (b2 - 4ac)]/2a

Roots of Quadratic Equation:

  • x = [-b ± D]/2a

  • D = b2 - 4ac

Nature of Roots of Quadratic Equation:

  • D > 0: Roots are real and distinct.

  • D = 0: Roots are real and equal.

  • D < 0: Roots are imaginary.

The sum of Roots:

  • S = α + β = -b/a

Product of Roots:

  • P = αβ = c/a

Quadratic Equation in terms of Roots:

  • x2 - (α + β)x + αβ = 0

Common Roots of Quadratic Equations:

  • One common root: (b1c2 - b2c1) / (c1a2 - c2a1) = (c1a2 - c2a1) / (a1b2 - a2b1)

  • Both roots common: a1/a2 = b1/b2 = c1/c2

Quadratic Equation Simplified Form:

  • ax2 + bx + c = 0 or [(x + b/2a)2 -D/(4a2)]

Extreme Values of Quadratic Equation:

  • If a > 0, minimum value = (4ac - b2)/4a at x = -b/(2a)

  • If a < 0, maximum value = (4ac - b2)/4a at x = -b/(2a)

The sum of Roots of Cubic Equation:

  • If α, β, γ are roots of the cubic equation: ax3 + bx2 + cx + d = 0

α + β + γ = -b/a.

αβ + βγ + γα = c/a.

αβγ = -d/a.

Free download NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations PDF for CBSE Exam.

NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations (Intext Questions and Exercise)

Quadratic Equation Class 10 Excercise: 4.1

Q1 (i) Check whether the following are quadratic equations : (x+1)^2 = 2(x-3)

Answer:

We have L.H.S. (x+1)^2 = x^2+2x+1

Therefore, (x+1)^2 = 2(x-3) can be written as:

\Rightarrow x^2+2x+1 = 2x-6

i.e., x^2+7 = 0

Or x^2+0x+7 = 0

This equation is of type: ax^2+bx+c = 0 .

Hence, the given equation is a quadratic equation.

Q1 (ii) Check whether the following are quadratic equations : x^2 - 2x = (-2)(3-x)

Answer:

Given equation x^2 - 2x = (-2)(3-x) can be written as:

\Rightarrow x^2 -2x = -6+2x

i.e., x^2-4x+6 = 0

This equation is of type: ax^2+bx+c = 0 .

Hence, the given equation is a quadratic equation.

Q1 (iii) Check whether the following are quadratic equations : (x-2)(x+1) = (x-1)(x+3)

Answer:

L.H.S. (x-2)(x+1) can be written as:

= x^2+x-2x-2 = x^2-x-2

and R.H.S (x-1)(x+3) can be written as:

= x^2+3x-x-3 = x^2+2x-3

\Rightarrow x^2-x-2 = x^2+2x-3

i.e., 3x-1 = 0

The equation is of the type: ax^2+bx+c = 0,a\neq0 .

Hence, the given equation is not a quadratic equation since a=0.

Q1 (iv) Check whether the following are quadratic equations : (x-3)(2x+1) = x(x+5)

Answer:

L.H.S. (x-3)(2x+1) can be written as:

= 2x^2+x-6x-3 = 2x^2-5x-3

and R.H.S (x)(x+5) can be written as:

= x^2+5x

\Rightarrow 2x^2-5x-3 = x^2+5x

i.e., x^2-10x-3 = 0

This equation is of type: ax^2+bx+c = 0,a\neq0 .

Hence, the given equation is a quadratic equation.

Q1 (v) Check whether the following are quadratic equations : (2x -1)(x-3) = (x+5)(x-1)

Answer:

L.H.S. (2x-1)(x-3) can be written as:

= 2x^2-6x-x+3 = 2x^2-7x+3

and R.H.S (x+5)(x-1) can be written as:

=x^2-x+5x-5 = x^2+4x-5

\Rightarrow 2x^2-7x+3 = x^2+4x-5

i.e., x^2-11x+8 = 0

This equation is of type: ax^2+bx+c = 0,a \neq 0 .

Hence, the given equation is a quadratic equation.

Q1 (vi) Check whether the following are quadratic equations : x^2 +3x +1 = (x-2)^2

Answer:

L.H.S. x^2+3x+1

and R.H.S (x-2)^2 can be written as:

= x^2-4x+4

\Rightarrow x^2+3x+1 = x^2- 4x+4

i.e., 7x-3 = 0

This equation is NOT of type: ax^2+bx+c = 0 , a\neq0 .

Here a=0, hence, the given equation is not a quadratic equation.

Q1 (vii) Check whether the following are quadratic equations : (x+2)^3 = 2x(x^2 -1)

Answer:

L.H.S. (x+2)^3 can be written as:

= x^3+8+6x(x+2) =x^3+6x^2+12x+8

and R.H.S 2x(x^2-1) can be written as:

= 2x^3-2x

\Rightarrow x^3+6x^2+12x+8 = 2x^3-2x

i.e., x^3-6x^2-14x-8 = 0

This equation is NOT of type: ax^2+bx+c = 0 .

Hence, the given equation is not a quadratic equation.

Q1 (viii) Check whether the following are quadratic equations : x^3 -4x^2 -x +1 = (x -2)^3

Answer:

L.H.S. x^3 -4x^2 -x +1 ,

and R.H.S (x-2)^3 can be written as:

= x^3-6x^2+12x-8

\Rightarrow x^3-4x^2-x+1 = x^3-6x^2+12x-8

i.e., 2x^2-13x+9=0

This equation is of type: ax^2+bx+c = 0 .

Hence, the given equation is a quadratic equation.

Q2 (i) Represent the following situations in the form of quadratic equations : The area of a rectangular plot is 528m^2 . The length of the plot (in meters) is one more than twice its breadth. We need to find the length and breadth of the plot.

Answer:

Given the area of a rectangular plot is 528m^2 .

Let the breadth of the plot be 'b' .

Then, the length of the plot will be: = 2b +1 .

Therefore the area will be:

=b(2b+1)\ m^2 which is equal to the given plot area 528m^2 .

\Rightarrow 2b^2+b = 528

\Rightarrow 2b^2+b - 528 = 0

Hence, the length and breadth of the plot will satisfy the equation 2b^2+b - 528 = 0

Q2 (ii) Represent the following situations in the form of quadratic equations : The product of two consecutive positive integers is 306. We need to find the integers.

Answer:

Given the product of two consecutive integers is 306.

Let two consecutive integers be 'x' and 'x+1' .

Then, their product will be:

x(x+1) = 306

Or x^2+x- 306 = 0 .

Hence, the two consecutive integers will satisfy this quadratic equation x^2+x- 306 = 0 .

Q2 (iii) Represent the following situations in the form of quadratic equations: Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.

Answer:

Let the age of Rohan be 'x' years.

Then his mother age will be: 'x+26' years.

After three years,

Rohan's age will be 'x+3' years and his mother age will be 'x+29' years.

Then according to question,

The product of their ages 3 years from now will be:

\Rightarrow (x+3)(x+29) = 360

\Rightarrow x^2+3x+29x+87 = 360 Or

\Rightarrow x^2+32x-273 = 0

Hence, the age of Rohan satisfies the quadratic equation x^2+32x-273 = 0 .

Q2 (iv) Represent the following situations in the form of quadratic equations : A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.

Answer:

Let the speed of the train be 's' km/h.

The distance to be covered by the train is 480\ km .

\therefore The time taken will be

=\frac{480}{s}\ hours

If the speed had been 8\ km/h less, the time taken would be: \frac{480}{s-8}\ hours .

Now, according to question

\frac{480}{s-8} - \frac{480}{s} = 3

\Rightarrow \frac{480x - 480(x-8)}{(x-8)x} = 3

\Rightarrow 480x - 480x+3840 = 3(x-8)x

\Rightarrow 3840 = 3x^2-24x

\Rightarrow 3x^2 -24x-3840 = 0

Dividing by 3 on both the side

x^2 -8x-1280 = 0

Hence, the speed of the train satisfies the quadratic equation x^2 -8x-1280 = 0


Quadratic Equation Class 10 Excercise: 4.2

Q1 (i) Find the roots of the following quadratic equations by factorization: x^2 - 3x - 10 =0

Answer:

Given the quadratic equation: x^2 - 3x - 10 =0

Factorization gives, x^2 - 5x+2x - 10 =0

\Rightarrow x^2 - 5x+2x - 10 =0

\Rightarrow x(x-5) +2(x-5) =0

\Rightarrow (x-5)(x+2) =0

\Rightarrow x= 5\ or\ -2

Hence, the roots of the given quadratic equation are 5\ and\ -2 .

Q1 (ii) Find the roots of the following quadratic equations by factorization: 2x^2 + x - 6 = 0

Answer:

Given the quadratic equation: 2x^2 + x - 6 = 0

Factorisation gives, 2x^2 +4x-3x - 6 = 0

\Rightarrow 2x(x+2) -3(x+2) =0

\Rightarrow (x+2)(2x-3) = 0

\Rightarrow x= -2\ or\ \frac{3}{2}

Hence, the roots of the given quadratic equation are

-2\ and\ \frac{3}{2}

Q1 (iii) Find the roots of the following quadratic equations by factorization: \sqrt2x^2 + 7x + 5\sqrt2 = 0

Answer:

Given the quadratic equation: \sqrt2x^2 + 7x + 5\sqrt2 = 0

Factorization gives, \sqrt2x^2 + 5x+2x + 5\sqrt2 = 0

\Rightarrow x(\sqrt2 x +5) +\sqrt2 (\sqrt 2 x +5)= 0

\Rightarrow (\sqrt2 x +5)(x+\sqrt{2}) = 0

\Rightarrow x=\frac{-5}{\sqrt 2 }\ or\ -\sqrt 2

Hence, the roots of the given quadratic equation are

\frac{-5}{\sqrt 2 }\ and\ -\sqrt 2

Q1 (iv) Find the roots of the following quadratic equations by factorization: 2x^2 -x + \frac{1}{8} = 0

Answer:

Given the quadratic equation: 2x^2 -x + \frac{1}{8} = 0

Solving the quadratic equations, we get

16x^2-8x+1 = 0

Factorization gives, \Rightarrow 16x^2-4x-4x+1 = 0

\Rightarrow 4x(4x-1)-1(4x-1) = 0

\Rightarrow (4x-1)(4x-1) = 0

\Rightarrow x=\frac{1}{4}\ or\ \frac{1}{4}

Hence, the roots of the given quadratic equation are

\frac{1}{4}\ and\ \frac{1}{4}

Q1 (v) Find the roots of the following quadratic equations by factorization: 100x^2 -20x +1 = 0

Answer:

Given the quadratic equation: 100x^2 -20x +1 = 0

Factorization gives, 100x^2 -10x-10x +1 = 0

\Rightarrow 10x(10x-1)-10(10x-1) = 0

\Rightarrow (10x-1)(10x-1) = 0

\Rightarrow x=\frac{1}{10}\ or\ \frac{1}{10}

Hence, the roots of the given quadratic equation are

\frac{1}{10}\ and\ \frac{1}{10} .

Q2 Solve the problems given in Example 1. (i) x^2-45x+324 = 0 (ii) x^2-55x+750 = 0

Answer:

From Example 1 we get:

Equations:

(i) x^2-45x+324 = 0

Solving by factorization method:

Given the quadratic equation: x^2-45x+324 = 0

Factorization gives, x^2-36x-9x+324 = 0

\Rightarrow x(x-36) - 9(x-36) = 0

\Rightarrow (x-9)(x-36) = 0

\Rightarrow x=9\ or\ 36

Hence, the roots of the given quadratic equation are x=9\ and \ 36 .

Therefore, John and Jivanti have 36 and 9 marbles respectively in the beginning.

(ii) x^2-55x+750 = 0

Solving by factorization method:

Given the quadratic equation: x^2-55x+750 = 0

Factorization gives, x^2-30x-25x+750 = 0

\Rightarrow x(x-30) -25(x-30) = 0

\Rightarrow (x-25)(x-30) = 0

\Rightarrow x=25\ or\ 30

Hence, the roots of the given quadratic equation are x=25\ and \ 30 .

Therefore, the number of toys on that day was 30\ or\ 25.

Q3 Find two numbers whose sum is 27 and the product is 182.

Answer:

Let two numbers be x and y .

Then, their sum will be equal to 27 and the product equals 182.

x+y = 27 ...............................(1)

xy =182 .................................(2)

From equation (2) we have:

y = \frac{182}{x}

Then putting the value of y in equation (1), we get

x+\frac{182}{x} = 27

Solving this equation:

\Rightarrow x^2-27x+182 = 0

\Rightarrow x^2-13x-14x+182 = 0

\Rightarrow x(x-13)-14(x-13) = 0

\Rightarrow (x-14)(x-13) = 0

\Rightarrow x = 13\ or\ 14

Hence, the two required numbers are 13\ and \ 14 .

Q4 Find two consecutive positive integers, the sum of whose squares is 365.

Answer:

Let the two consecutive integers be 'x'\ and\ 'x+1'.

Then the sum of the squares is 365.

. x^2+ (x+1)^2 = 365

\Rightarrow x^2+x^2+1+2x = 365

\Rightarrow x^2+x-182 = 0

\Rightarrow x^2 - 13x+14x+182 = 0

\Rightarrow x(x-13)+14(x-13) = 0

\Rightarrow (x-13)(x-14) = 0

\Rightarrow x =13\ or\ 14

Hence, the two consecutive integers are 13\ and\ 14 .

Q5 The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.

Answer:

Let the length of the base of the triangle be b\ cm .

Then, the altitude length will be: b-7\ cm .

Given if hypotenuse is 13\ cm .

Applying the Pythagoras theorem; we get

Hypotenuse^2 = Perpendicular^2 + Base^2

So, (13)^2 = (b-7)^2 +b^2

\Rightarrow 169 = 2b^2+49-14b

\Rightarrow 2b^2-14b-120 = 0 Or b^2-7b-60 = 0

\Rightarrow b^2-12b+5b-60 = 0

\Rightarrow b(b-12) + 5(b-12) = 0

\Rightarrow (b-12)(b+5) = 0

\Rightarrow b= 12\ or\ -5

But, the length of the base cannot be negative.

Hence the base length will be 12\ cm .

Therefore, we have

Altitude length = 12cm -7cm = 5cm and Base length = 12\ cm

Q6 A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was Rs 90, find the number of articles produced and the cost of each article.

Answer:

Let the number of articles produced in a day = x

The cost of production of each article will be =2x+3

Given the total production on that day was Rs.90 .

Hence we have the equation;

x(2x+3) = 90

2x^2+3x-90 = 0

\Rightarrow 2x^2+15x-12x-90 = 0

\Rightarrow x(2x+15) - 6(2x+15) = 0

\Rightarrow (2x+15)(x-6) = 0

\Rightarrow x =-\frac{15}{2}\ or\ 6

But, x cannot be negative as it is the number of articles.

Therefore, x=6 and the cost of each article = 2x+3 = 2(6)+3 = 15

Hence, the number of articles is 6 and the cost of each article is Rs.15.


Class 10 Maths Chapter 4 Quadratic Equations Excercise: 4.3

Q1 (i) Find the roots of the following quadratic equations, if they exist, by the method of completing the square 2x^2 - 7x +3 = 0

Answer:

Given equation: 2x^2 - 7x +3 = 0

On dividing both sides of the equation by 2, we obtain

\Rightarrow x^2-\frac{7}{2}x+\frac{3}{2} = 0

\Rightarrow (x-\frac{7}{4})^2 + \frac{3}{2} - \frac{49}{16} = 0

\Rightarrow (x-\frac{7}{4})^2 = \frac{49}{16} - \frac{3}{2}

\Rightarrow (x-\frac{7}{4})^2 =\frac{25}{16}

\Rightarrow (x-\frac{7}{4}) =\pm \frac{5}{4}

\Rightarrow x =\frac{7}{4}\pm \frac{5}{4}

\Rightarrow x = \frac{7}{4}+\frac{5}{4}\ or\ x = \frac{7}{4} - \frac{5}{4}

\Rightarrow x = 3\ or\ \frac{1}{2}

Q1 (ii) Find the roots of the following quadratic equations, if they exist, by the method of completing the square 2x^2 + x -4 = 0

Answer:

Given equation: 2x^2 + x -4 = 0

On dividing both sides of the equation by 2, we obtain

\Rightarrow x^2+\frac{1}{2}x-2 = 0

Adding and subtracting \frac{1}{16} in the equation, we get

\Rightarrow (x+\frac{1}{4})^2 -2 - \frac{1}{16} = 0

\Rightarrow (x+\frac{1}{4})^2 =2+\frac{1}{16}

\Rightarrow (x+\frac{1}{4})^2 = \frac{33}{16}

\Rightarrow (x+\frac{1}{4}) =\pm \frac{\sqrt{33}}{4}

\Rightarrow x =\pm \frac{\sqrt{33}}{4} -\frac{1}{4}

\Rightarrow x = \frac{\pm \sqrt{33} - 1}{4}

\Rightarrow x = \frac{ \sqrt{33} - 1}{4}\ or\ x = \frac{ -\sqrt{33} - 1}{4}

Q1 (iii) Find the roots of the following quadratic equations, if they exist, by the method of completing the square 4x^2 + 4\sqrt3 + 3 = 0

Answer:

Given equation: 4x^2 + 4\sqrt3 + 3 = 0

On dividing both sides of the equation by 4, we obtain

\Rightarrow x^2+\sqrt3x+\frac{3}{4} = 0

Adding and subtracting (\frac{\sqrt3}{2})^2 in the equation, we get

\Rightarrow (x+\frac{\sqrt3}{2})^2 +\frac{3}{4} - (\frac{\sqrt3}{2})^2 = 0

\Rightarrow (x+\frac{\sqrt3}{2})^2 = \frac{3}{4} - \frac{3}{4} = 0

\Rightarrow (x+\frac{\sqrt3}{2}) = 0\ or\ (x+\frac{\sqrt3}{2}) = 0

Hence there are the same roots and equal:

\Rightarrow x = \frac{-\sqrt3}{2}\ or\ \frac{-\sqrt3}{2}

Q2 (iv) Find the roots of the following quadratic equations, if they exist, by the method of completing the square 2x^2 + x + 4 = 0

Answer:

Given equation: 2x^2 + x + 4 = 0

On dividing both sides of the equation by 2, we obtain

\Rightarrow x^2+\frac{x}{2}+2 = 0

Adding and subtracting (\frac{1}{4})^2 in the equation, we get

\Rightarrow (x+\frac{1}{4})^2 +2- (\frac{1}{4})^2 = 0

\Rightarrow (x+\frac{1}{4})^2 = \frac{1}{16} -2 = \frac{-31}{16}

\Rightarrow (x+\frac{1}{4}) = \pm \frac{\sqrt{-31}}{4}

\Rightarrow x = \pm \frac{\sqrt{-31}}{4} - \frac{1}{4}

\Rightarrow x = \frac{\sqrt{-31}-1}{4} \ or\ x = \frac{-\sqrt{-31}-1}{4}

Here the real roots do not exist (in the higher studies we will study how to find the root of such equations).

Q2 Find the roots of the quadratic equations given in Q.1 above by applying the quadratic formula.

Answer:

(i) 2x^2-7x+3 = 0

The general form of a quadratic equation is : ax^2+bx+c = 0 , where a, b, and c are arbitrary constants.

Hence on comparing the given equation with the general form, we get

a = 2,\ b = -7\ c = 3

And the quadratic formula for finding the roots is:

x= \frac{-b \pm \sqrt{b^2-4ac}}{2a}

Substituting the values in the quadratic formula, we obtain

\Rightarrow x= \frac{7 \pm \sqrt{49-24}}{4}

\Rightarrow x= \frac{7 \pm 5}{4}

\Rightarrow x= \frac{7 + 5}{4} = 3\ or\ x= \frac{7 - 5}{4} = \frac{1}{2}

Therefore, the real roots are: x =3,\ \frac{1}{2}


(ii) 2x^2+x-4 = 0

The general form of a quadratic equation is : ax^2+bx+c = 0 , where a, b, and c are arbitrary constants.

Hence on comparing the given equation with the general form, we get

a = 2,\ b = 1\ c =-4

And the quadratic formula for finding the roots is:

x= \frac{-b \pm \sqrt{b^2-4ac}}{2a}

Substituting the values in the quadratic formula, we obtain

\Rightarrow x= \frac{-1 \pm \sqrt{1+32}}{4}

\Rightarrow x= \frac{-1 \pm \sqrt{33}}{4}

\Rightarrow x= \frac{-1 + \sqrt{33}}{4} \ or\ x= \frac{-1 - \sqrt{33}}{4}

Therefore, the real roots are: x = \frac{-1+\sqrt{33}}{4}\ or\ \frac{-1-\sqrt{33}}{4}

(iii) 4x^2+4\sqrt3x+3 = 0

The general form of a quadratic equation is : ax^2+bx+c = 0 , where a, b, and c are arbitrary constants.

Hence on comparing the given equation with the general form, we get

a = 4,\ b = 4\sqrt{3}\ c =3

And the quadratic formula for finding the roots is:

x= \frac{-b \pm \sqrt{b^2-4ac}}{2a}

Substituting the values in the quadratic formula, we obtain

\Rightarrow x= \frac{-4\sqrt{3} \pm \sqrt{48-48}}{8}

\Rightarrow x= \frac{-4\sqrt{3} \pm 0}{8}

Therefore, the real roots are: x = \frac{-\sqrt{3}}{2}\ or\ \frac{-\sqrt{3}}{2}

(iv) 2x^2+x+4 = 0

The general form of a quadratic equation is : ax^2+bx+c = 0 , where a, b, and c are arbitrary constants.

Hence on comparing the given equation with the general form, we get

a = 2,\ b = 1,\ c =4

And the quadratic formula for finding the roots is:

x= \frac{-b \pm \sqrt{b^2-4ac}}{2a}

Substituting the values in the quadratic formula, we obtain

\Rightarrow x= \frac{-1 \pm \sqrt{1-32}}{4}

\Rightarrow x= \frac{-1 \pm \sqrt{-31}}{4}

Here the term inside the root is negative

Therefore there are no real roots for the given equation.

Q3 (i) Find the roots of the following equations: x - \frac{1}{x} = 3, x\neq 0

Answer:

Given equation: x - \frac{1}{x} = 3, x\neq 0

So, simplifying it,

\Rightarrow \frac{x^2-1}{x} = 3

\Rightarrow x^2-3x-1 = 0

Comparing with the general form of the quadratic equation: ax^2+bx+c = 0 , we get

a=1,\ b=-3,\ c=-1

Now, applying the quadratic formula to find the roots:

x= \frac{-b \pm \sqrt{b^2-4ac}}{2a}

\Rightarrow x= \frac{3 \pm \sqrt{9+4}}{2}

\Rightarrow x= \frac{3 \pm \sqrt{13}}{2}

Therefore, the roots are

\Rightarrow x = \frac{3+\sqrt{13}}{2}\ or\ \frac{3 - \sqrt{13}}{2}

Q3 (ii) Find the roots of the following equations: \frac{1}{x+4} - \frac{1}{x- 7} = \frac{11}{30},\ x\neq -4,7

Answer:

Given equation: \frac{1}{x+4} - \frac{1}{x- 7} = \frac{11}{30},\ x\neq -4,7

So, simplifying it,

\Rightarrow \frac{x-7-x-4}{(x+4)(x-7)} = \frac{11}{30}

\Rightarrow \frac{-11}{(x+4)(x-7)} = \frac{11}{30}

\Rightarrow (x+4)(x-7) = -30

\Rightarrow x^2-3x-28 = -30 or \Rightarrow x^2-3x+2 = 0

Can be written as:

\Rightarrow x^2-x-2x+2 = 0

\Rightarrow x(x-1) -2(x-1) = 0

\Rightarrow (x-2)(x-1) = 0

Hence the roots of the given equation are:

\Rightarrow x = 1\ or\ 2

Q4 The sum of the reciprocals of Rehman’s ages, (in years) 3 years ago and 5 years from now is \frac{1}{3} . Find the present age.

Answer:

Let the present age of Rehman be 'x' years.

Then, 3 years ago, his age was (x-3) years.

and 5 years later, his age will be (x+5) years.

Then according to the question we have,

\frac{1}{(x-3)}+\frac{1}{(x+5)} = \frac{1}{3}

Simplifying it to get the quadratic equation:

\Rightarrow \frac{x+5+x-3}{(x-3)(x+5)} = \frac{1}{3}

\Rightarrow \frac{2x+2}{(x-3)(x+5)} = \frac{1}{3}

\Rightarrow 3(2x+2)= (x-3)(x+5)

\Rightarrow 6x+6 = x^2+2x-15

\Rightarrow x^2-4x-21 = 0

\Rightarrow x^2-7x+3x-21 = 0

\Rightarrow x(x-7)+3(x-7) = 0

\Rightarrow (x-7)(x+3) = 0

Hence the roots are: \Rightarrow x = 7,\ -3

However, age cannot be negative

Therefore, Rehman is 7 years old in the present.

Q5 In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.

Answer:

Let the marks obtained in Mathematics be 'm' then, the marks obtain in English will be '30-m'.

Then according to the question:

(m+2)(30-m-3) = 210

Simplifying to get the quadratic equation:

\Rightarrow m^2-25m+156 = 0

Solving by the factorizing method:

\Rightarrow m^2-12m-13m+156 = 0

\Rightarrow m(m-12)-13(m-12) = 0

\Rightarrow (m-12)(m-13) = 0

\Rightarrow m = 12,\ 13

We have two situations when,

The marks obtained in Mathematics is 12, then marks in English will be 30-12 = 18.

Or,

The marks obtained in Mathematics is 13, then marks in English will be 30-13 = 17.

Q6 The diagonal of a rectangular field is 60 meters more than the shorter side. If the longer side is 30 meters more than the shorter side, find the sides of the field.

Answer:

Let the shorter side of the rectangle be x m.

Then, the larger side of the rectangle wil be = (x+30)\ m .

Diagonal of the rectangle:

= \sqrt{x^2+(x+30)^2}\ m

It is given that the diagonal of the rectangle is 60m more than the shorter side.

Therefore,

\sqrt{x^2+(x+30)^2} = x+60

\Rightarrow x^2+(x+30)^2 = (x+60)^2

\Rightarrow x^2+x^2+900+60x = x^2+3600+120x

\Rightarrow x^2-60x-2700 = 0

Solving by the factorizing method:

\Rightarrow x^2-90x+30x-2700 = 0

\Rightarrow x(x-90)+30(x-90)= 0

\Rightarrow (x+30)(x-90) = 0

Hence, the roots are: x = 90,\ -30

But the side cannot be negative.

Hence the length of the shorter side will be: 90 m

and the length of the larger side will be (90+30)\ m =120\ m

Q7 The difference of squares of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the two numbers.

Answer:

Given the difference of squares of two numbers is 180.

Let the larger number be 'x' and the smaller number be 'y'.

Then, according to the question:

x^2-y^2 = 180 and y^2 = 8x

On solving these two equations:

\Rightarrow x^2-8x =180

\Rightarrow x^2-8x -180 = 0

Solving by the factorizing method:

\Rightarrow x^2-18x+10x -180 = 0

\Rightarrow x(x-18)+10(x-18) = 0

\Rightarrow (x-18)(x+10) = 0

\Rightarrow x=18,\ -10

As the negative value of x is not satisfied in the equation: y^2 = 8x

Hence, the larger number will be 18 and a smaller number can be found by,

y^2 = 8x putting x = 18, we obtain

y^2 = 144\ or\ y = \pm 12 .

Therefore, the numbers are 18\ and\ 12 or 18\ and\ -12 .

Q8 A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

Answer:

Let the speed of the train be x\ km/hr.

Then, time taken to cover 360km will be:

=\frac{360}{x}\ hr

According to the question,

\Rightarrow (x+5)\left ( \frac{360}{x}-1 \right ) = 360

\Rightarrow 360-x+\frac{1800}{x} - 5 = 360

Making it a quadratic equation.

\Rightarrow x^2+5x-1800 = 0

Now, solving by the factorizing method:

\Rightarrow x^2+45x-40x-1800 = 0

\Rightarrow x(x+45)-40(x+45) = 0

\Rightarrow (x-40)(x+45) = 0

\Rightarrow x = 40,\ -45

However, the speed cannot be negative hence,

The speed of the train is 40\ km/hr .

Q9 Two water taps together can fill a tank in 9\frac{3}{8} hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.

Answer:

Let the time taken by the smaller pipe to fill the tank be x\ hr.

Then, the time taken by the larger pipe will be: (x-10)\ hr .

The fraction of the tank filled by a smaller pipe in 1 hour:

= \frac{1}{x}

The fraction of the tank filled by the larger pipe in 1 hour.

= \frac{1}{x-10}
Given that two water taps together can fill a tank in 9\frac{3}{8} = \frac{75}{8} hours.

Therefore,

\Rightarrow \frac{1}{x}+\frac{1}{x-10} = \frac{8}{75}

\Rightarrow \frac{x-10+x}{x(x-10)} = \frac{8}{75}

\Rightarrow \frac{2x-10}{x(x-10)} = \frac{8}{75}

Making it a quadratic equation:

\Rightarrow 150x-750 = 8x^2-80x

\Rightarrow 8x^2-230x+750 = 0

\Rightarrow 8x^2-200x-30x+750 = 0

\Rightarrow 8x(x-25) - 30(x-25) = 0

\Rightarrow (x-25)(8x+30) = 0

Hence the roots are \Rightarrow x = 25,\ \frac{-30}{8}

As time is taken cannot be negative:

Therefore, time is taken individually by the smaller pipe and the larger pipe will be 25 and 25-10 =15 hours respectively.

Q10 An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/h more than that of the passenger train, find the average speed of the two trains.

Answer:

Let the average speed of the passenger train be x\ km/hr .

Given the average speed of the express train = (x+11)\ km/hr

also given that the time taken by the express train to cover 132 km is 1 hour less than the passenger train to cover the same distance.

Therefore,

\Rightarrow \frac{132}{x} - \frac{132}{x+11} = 1

\Rightarrow 132\left [ \frac{x+11-x}{x(x+11)} \right ] = 1

\Rightarrow \frac{132\times11}{x(x+11)} = 1

Can be written as quadratic form:

\Rightarrow x^2+11x-1452 = 0

\Rightarrow x^2+44x-33x-1452 = 0

\Rightarrow x(x+44)-33(x+44)= 0

\Rightarrow (x+44)(x-33) = 0

Roots are: \Rightarrow x = -44,\ 33

As the speed cannot be negative.

Therefore, the speed of the passenger train will be 33\ km/hr and

The speed of the express train will be 33+11 = 44\ km/hr .

Q11 Sum of the areas of two squares is 468 m 2 . If the difference of their perimeters is 24 m, find the sides of the two squares.

Answer:

Let the sides of the squares be 'x'\ and\ 'y' . (NOTE: length are in meters)

And the perimeters will be: 4x\ and\ 4y respectively.

Areas x^2\ and\ y^2 respectively.

It is given that,

x^2 + y^2 = 468\ m^2 .................................(1)

4x-4y = 24\ m .................................(2)

Solving both equations:

x-y = 6 or x= y+6 putting in equation (1), we obtain

(y+6)^2 +y^2 = 468

\Rightarrow 2y^2+36+12y = 468

\Rightarrow y^2+6y - 216 = 0

Solving by the factorizing method:

\Rightarrow y^2+18y -12y-216 = 0

\Rightarrow y(y+18) -12(y+18) = 0

\Rightarrow (y+18)(y-12)= 0

Here the roots are: \Rightarrow y = -18,\ 12

As the sides of a square cannot be negative.

Therefore, the sides of the squares are 12m and (12\ m+6\ m) = 18\ m .


Quadratic Equation Class 10 Excercise: 4.4

Q1 (i) Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:

2x^2 - 3x +5 = 0

Answer:

For a quadratic equation, ax^2+bx+c = 0 the value of discriminant determines the nature of roots and is equal to:

D = b^2-4ac

If D>0 then roots are distinct and real.

If D<0 then no real roots.

If D= 0 then there exists two equal real roots.

Given the quadratic equation, 2x^2 - 3x +5 = 0 .

Comparing with general to get the values of a,b,c.

a = 2, b =-3,\ c= 5

Finding the discriminant:

D= (-3)^2 - 4(2)(5) = 9-40 = -31

\because D<0

Here D is negative hence there are no real roots possible for the given equation.

Q1 (ii) Find the nature of the roots of the following quadratic equations. If the real roots exist, find them: 3x^2 - 4\sqrt3x + 4 = 0

Answer:

b^2-4ac=(-4\sqrt{3})^2-(4\times4\times3)=48-48=0

Here the value of discriminant =0, which implies that roots exist and the roots are equal.

The roots are given by the formula

x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}=\frac{4\sqrt{3}\pm\sqrt{0}}{2\times3}=\frac{2}{\sqrt{3}}

So the roots are

\frac{2}{\sqrt{3}},\ \frac{2}{\sqrt{3}}

Q1 (iii) Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:

2x^2 - 6x + 3 = 0

Answer:

The value of the discriminant

b^2-4ac=(-6)^2-4\times2\times3=12

The discriminant > 0. Therefore the given quadratic equation has two distinct real root

roots are

x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}=\frac{-6\pm\sqrt{12}}{2\times2}=\frac{3}{2}\pm\frac{\sqrt{3}}{2}

So the roots are

\frac{3}{2}+\frac{\sqrt{3}}{2}, \frac{3}{2}-\frac{\sqrt{3}}{2}

Q2 (i) Find the values of k for each of the following quadratic equations so that they have two equal roots.

2x^2 + kx + 3 = 0

Answer:

For two equal roots for the quadratic equation: ax^2+bx+c =0

The value of the discriminant D= 0 .

Given equation: 2x^2 + kx + 3 = 0

Comparing and getting the values of a,b, and, c.

a = 2, \ b = k,\ c = 3

The value of D = b^2-4ac = (k)^2 - 4(2)(3)

\Rightarrow (k)^2 = 24

Or, \Rightarrow k=\pm \sqrt{24} = \pm 2\sqrt{6}

Q2 (ii) Find the values of k for each of the following quadratic equations so that they have two equal roots

kx(x-2) + 6 = 0

Answer:

For two equal roots for the quadratic equation: ax^2+bx+c =0

The value of the discriminant D= 0 .

Given equation: kx(x-2) + 6 = 0

Can be written as: kx^2-2kx+6 = 0

Comparing and getting the values of a,b, and, c.

a = k, \ b = -2k,\ c = 6

The value of D = b^2-4ac = (-2k)^2 - 4(k)(6) = 0

\Rightarrow 4k^2 - 24k = 0

\Rightarrow 4k(k-6) = 0

\Rightarrow k= 0\ or\ 6

But k= 0 is NOT possible because it will not satisfy the given equation.

Hence the only value of k is 6 to get two equal roots.

Q3 Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m 2 ? If so, find its length and breadth.

Answer:

Let the breadth of mango grove be 'b' .

Then the length of mango grove will be '2b' .

And the area will be:

Area = (2b)(b) = 2b^2

Which will be equal to 800m^2 according to question.

\Rightarrow 2b^2 = 800m^2

\Rightarrow b^2 - 400 = 0

Comparing to get the values of a,b,c .

a=1, \ b= 0 , \ c = -400

Finding the discriminant value:

D = b^2-4ac

\Rightarrow 0^2-4(1)(-400) = 1600

Here, D>0

Therefore, the equation will have real roots.

And hence finding the dimensions:

\Rightarrow b^2 - 400 = 0

\Rightarrow b = \pm 20

As negative value is not possible, hence the value of breadth of mango grove will be 20m.

And the length of mango grove will be: = 2\times10 = 40m

Q4 Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.

Answer:

Let the age of one friend be x\ years.

and the age of another friend will be: (20-x)\ years.

4 years ago, their ages were, x-4\ years and 20-x-4 \ years .

According to the question, the product of their ages in years was 48.

\therefore (x-4)(20-x-4) = 48

\Rightarrow 16x-64-x^2+4x= 48

\Rightarrow -x^2+20x-112 = 0 or \Rightarrow x^2-20x+112 = 0

Now, comparing to get the values of a,\ b,\ c .

a = 1,\ b= -20,\ c =112

Discriminant value D = b^2-4ac = (-20)^2 -4(1)(112) = 400-448 = -48

As D<0 .

Therefore, there are no real roots possible for this given equation and hence,

This situation is NOT possible.

Q5 Is it possible to design a rectangular park of perimeter 80 m and area 400 m 2 ? If so, find its length and breadth.

Answer:

Let us assume the length and breadth of the park be 'l'\ and\ 'b' respectively.

Then, the perimeter will be P = 2(l+b) = 80

\Rightarrow l+b = 40\ or\ b = 40 - l

The area of the park is:

Area = l\times b = l(40-l) = 40l - l^2

Given : 40l - l^2 = 400

l^2 - 40l +400 = 0

Comparing to get the values of a, b and c.

The value of the discriminant D = b^2-4ac

\Rightarrow = b^2-4ac = (-40)^2 - 4(1)(400) = 1600 -1600 = 0

As D = 0 .

Therefore, this equation will have two equal roots.

And hence the roots will be:

l =\frac{-b}{2a}

l =\frac{-40}{2(1)} = \frac{40}{2} =20

Therefore, the length of the park, l =20\ m

and breadth of the park b = 40-l = 40 -20 = 20\ m .

Topics of Class 10 Maths Chapter 4 Quadratic Equations

  • Representation of situation in a quadratic equation.

  • Checking if an equation is quadratic or not.

  • Solving a quadratic equation using factorization/ roots of quadratic solutions.

  • The solution of the quadratic equation using completing the square method.

  • Solving a quadratic equation using the Sridharacharya formula.

  • Product of roots in a quadratic equation.

  • Sum of roots in a quadratic equation.

There are 4 exercise in Class 10 Maths chapter 4. Get the exercise wise solutions from the following links.

NCERT Books and NCERT Syllabus

Key Features For Chapter 4 Maths Class 10

Expertly Crafted: Skilled teachers at Careers360 create these NCERT Solutions with great care.

Accuracy Guaranteed: Class 10 maths chapter 4 solutions are entirely correct, making them perfect for students getting ready for their CBSE board exams.

Thorough Explanation: Even the smallest details are explained to help students feel more confident when facing other competitive exams.

Step-by-Step Answers: Class 10 maths ncert chapter 4 solutions to the textbook exercises are provided step by step. This helps students not only get the right final answers but also understand each part of the process, which can lead to better scores.

NCERT solutions for class 10 Maths - Chapter Wise

Chapter No.

Chapter Name

Chapter 1

Real Numbers

Chapter 2

Polynomials

Chapter 3

Pair of Linear Equations in Two Variables

Chapter 4

Quadratic Equations

Chapter 5

Arithmetic Progressions

Chapter 6

Triangles

Chapter 7

Coordinate Geometry

Chapter 8

Introduction to Trigonometry

Chapter 9

Some Applications of Trigonometry

Chapter 10

Circles

Chapter 11

Constructions

Chapter 12

Areas Related to Circles

Chapter 13

Surface Areas and Volumes

Chapter 14

Statistics

Chapter 15

Probability

How To use Solutions Of Quadratic Equation Class 10 ?

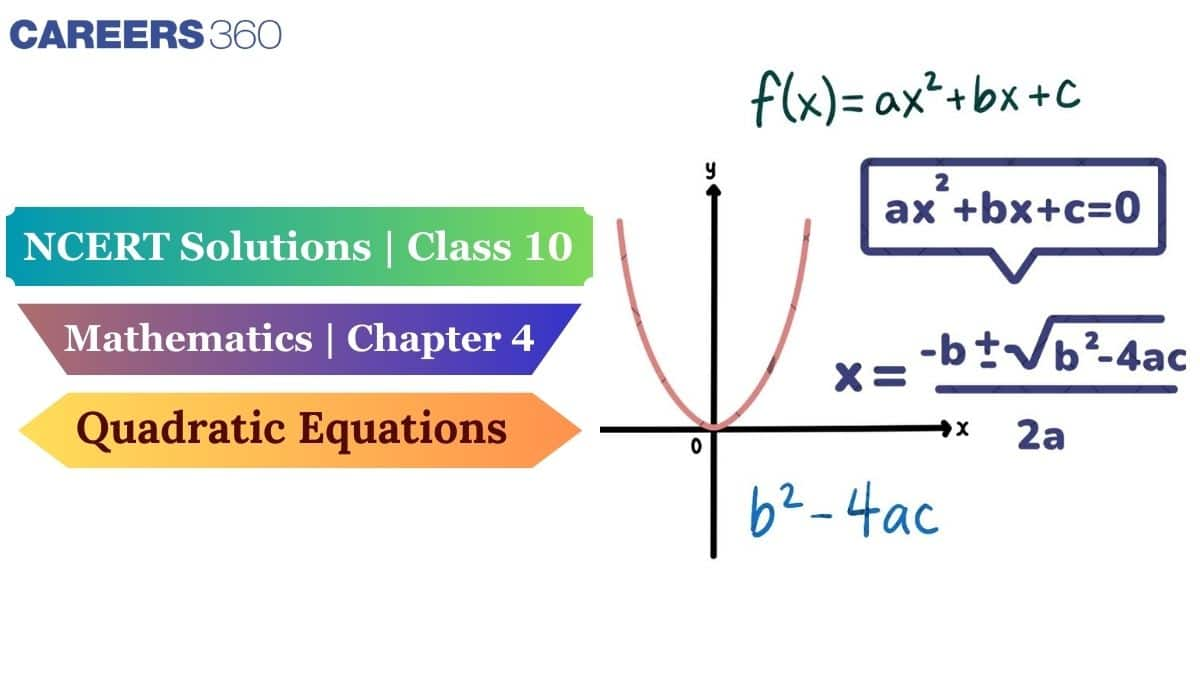
  • First of all list down all the questions in which you need assistance and go through the NCERT Solutions For Class 10 Maths Chapter 4 Quadratic Equations of that particular question.

  • When you complete the first step then your next target should be previous papers. You can pick past year papers and practice them thoroughly.

  • Once you complete NCERTs and previous year papers, try to solve the questions of that particular chapter from different state board books.

NCERT Solutions of Class 10 - Subject Wise

NCERT Exemplar solutions - Subject Wise

Frequently Asked Questions (FAQs)

1. What are the important concepts learned in the NCERT Solutions for chapter 4 maths class 10 Quadratic Equations?

Class 10 maths chapter 4 solutions required multiple concepts including what is an equation, how to get the solution of an equation, methods of quadratic equation solution, the factoring method for solving a quadratic equation, the quadratic formula for solving a quadratic equation, the nature of roots of a quadratic equation, graphs of quadratic equations, and many.

2. What are the important topics covered in the NCERT Solutions for Class 10 Maths Chapter 4?

Chapter 4 quadratic equation class 10 ncert solutions contain multiple topics like Quadratic equations, Solutions of a quadratic equation, Discriminant of a quadratic equation, Factoring method for solving a quadratic equation, Quadratic formula for solving a quadratic equation, Nature of roots of a quadratic equation, and Graphs of quadratic equations.

3. How do you download the Class 10 Maths Quadratic Equations NCERT Textbooks PDF?

Students can visit the NCERT official website. There they can find options to select class, subject, and book title. Using these inputs students can download NCERT chapter 4 maths class 10 which is quadratic equations class 10 pdf. Students can also find solutions to these NCERTs from Careers360's official website

4. How do you solve a quadratic equation in Class 10?

There are multiple methods to solve a quadratic equation including the factoring method, quadratic formula method, graphical method, and many others. These methods depend on the type of quadratic equation so first to know what is quadratic polynomial type and then apply the above methods to find a quadratic polynomial solution.

5. Which of the following is a quadratic equation?

To determine whether an equation is a quadratic equation, you can look for two conditions: firstly, the highest power of the variable is 2 and secondly, the coefficient of the x^2 term (that is, the "a" in the equation) is not equal to zero. These two are some examples of quadratic equations 2x^2+3x+5 and x^2+5x+6.

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Schools in Gurugram, Faridabad to hold classes in hybrid mode due to air pollution
CBSE files police complaint against two Delhi schools for submitting fake land certificates
Several Delhi schools receive bomb threat; fifth incident in nine days
Schools, colleges in Delhi NCR to switch to hybrid mode in view of air pollution
‘Take action’ on 22,298 unrecognised schools in UDISE Plus by March: Education ministry to states
Shiv Nadar School concludes 'Anandam 2024'; celebrating art, creativity in digital age
Jaipur: 10 students hospitalised after suspected gas leak at Mahesh Nagar coaching institute
Back to top