NCERT Exemplar Class 10 Maths Solutions Chapter 10 Constructions

Question 1:

To divide a line segment AB in the ratio $5:7$, first, a ray AX is drawn so that $\angle BAX$ is an acute angle, and then at equal distances, points are marked on the ray AX such that the minimum number of these points is
(A) 8 (B) 10 (C) 11 (D) 12

Answer: (D) 12
Solution
Given: $\angle BAX$ is an acute angle.
The required ratio is $5:7$
Let m = 5, n = 7

Steps of construction
1. Draw any ray AX making an acute angle with AB.
2. Locate 12 points on AX at equal distances. (Because here $m+n= 12$)
3. Join $A_{12}B$
4. Through the point $A_{5}$ draw a line parallel to $A_{12}B$ intersecting AB at the point P.
Then $AP:PB= 5:7$
$\because A_{5}P\parallel A_{12}B$
$\therefore \frac{AA_{5}}{A_{5}A_{12}}= \frac{AP}{PB}$ (By Basic Proportionality theorem)
By construction $\frac{AA_{5}}{A_{5}A_{12}}= \frac{5}{7}$
$\therefore \frac{AP}{PB}= \frac{5}{7}$
Hence, the number of points is 12.

Question 2:

To divide a line segment AB in the ratio $4:7$, a ray AX is drawn first such that $\angle BAX$ is an acute angle and then points $A_{1}, A_{2 }, A_{3}\cdots$ are located at equal distances on the ray AX and the point B is joined to:
(A) A₁₂ (B) A₁₁ (C) A₁₀ (D) A₉

Answer: (B) A₁₁
Solution
Given: $\angle BAX$ is an acute angle
The required ratio is $4:7$
Let m = 4, n = 7
$m+n= 4+7= 11$

Steps of construction
1. Draw any ray AX making an acute angle with AB.
2. Locate 11 points on AX at equal distances (because m + n = 11)
3. Join $A_{11}B$
4. Through the point A4 draw a line parallel to $A_{11}B$ intersecting AB at the point P.
Then $AP:PB= 4:7$
Hence, point B is joined to A₁₁.

Question 3:

To divide a line segment AB in the ratio $5:6$, draw a ray AX such that $\angle BAX$ is an acute angle, then draw a ray BY parallel to AX and the points $A_{ 1}, A_ {2}, A_{3}\cdots$and $B _{1}, B_{2}, B_{3}\cdots$are located at equal distances on ray AX and BY, respectively. Then the points joined are
(A) A₅ and B₆ (B) A­ and B₅ (C) A₄ and B₅ (D) A₅ and B₄

Answer: (A) A₅ and B₆

Solution
Given: $\angle BAX$ and $\angle ABY$ both are acute angles and AX parallel to BY
The required ratio is $5:6$
Let m = 5 , n = 6

Steps of construction
1. Draw any ray AX making an acute angle with AB.
2. Draw a ray $BY\parallel AX$.
3. Locate the points $A_{1},A_{2},A_{3},A_{4},A_{5}$ on AX at equal distances
4. Locate the points $B_{1}, B_{2}, B_{3 }, B_{ 4 }, B_{5}$ on BY at a distance equal to the distance between points on the AX line.
5. Join $A_{5}B_{6}$.
Let it intersect AB at a point C in the figure.
Then $AC:CB= 5:6$
Here $\bigtriangleup AA_{5}C$ is similar to $\bigtriangleup BB_{6}C$
Then $\frac{AA_{5}}{BB_{6}}= \frac{5}{6}= \frac{AC}{BC}$
$\therefore$by construction $\frac{AA_{5}}{BB_{6}}= \frac{5}{6}$
$\therefore \frac{AC}{BC}= \frac{5}{6}$
$\therefore$ Points joined one A₅ and B₆.

Question 4:

To construct a triangle similar to a given $\bigtriangleup ABC$ with its sides of $\frac{3}{7}$ the corresponding sides of $\bigtriangleup ABC$, first, draw a ray BX such that CBX is an acute angle and X lies on the opposite side of A Aconcerningo BC. Then locate points B₁, B₂, B₃, ... on BX at equal distances, and the next step is to join
(A) B₁₀ to C (B) B₃ to C (C) B₇ to C (D) B₄ to C

Answer: (C) B₇ to C
Solution Given: $\angle CBX$ is an acute angle.

Steps of construction
1. Draw any ray BX making an angle with BC on the side opposite vertex A.
2. Locate 7 points on BX in equidistant
3. Now join B₇ to C
4. Draw a line through B₃${C}'$ parallel to B₇C .

Question 5:

To construct a triangle similar to a given $\bigtriangleup ABC$ with its sides $\frac{8}{5}$ of the corresponding sides of $\bigtriangleup ABC$ draw a ray BX such that $\angle CBX$ is an acute angle and X is on the opposite side of A concerning BC. The minimum number of points to be located at equal distances on ray BX is
(A) 5 (B) 8 (C) 13 (D) 3

Answer: (B) 8
Solution
To construct a triangle similar to a triangle, with its sides $\frac{8}{5}$ of the corresponding sides of a given triangle, the minimum number of points to be located at an equal distance is equal to the greater of 8 and 5 in $\frac{8}{5}$. Here $8> 5$
So, the minimum number of points to be located at equal distances on ray BX is 8.

Question 6:

To draw a pair of tangents to a circle which are inclined to each other at an Angle of $60^{\circ}$, it is required to draw tangents at the endpoints of those two radii of the circle, and the angle between them should be
(A) $135^{\circ}$ (B) $90^{\circ}$ (C) $60^{\circ}$ (D) $120^{\circ}$

Answer: (D) 120°
Solution
According to Question -

Given :$\angle QPR= 60^{\circ}$
Let $\angle QOR= x$
As we know, the angle between the agent and the radius of a circle is 90 degrees
$\angle PQO= \angle PRO= 90^{\circ}$
We know that $\angle PQO+ \angle PRO+ \angle QPR+\angle QOR= 360^{\circ}$
[$\because$ sum of interior angles of quadrilateral is $360^{\circ}$ ]
$90^{\circ}+90^{\circ}+x+60^{\circ}= 360^{\circ}$|
$240+x= 360^{\circ}$
$x= 120^{\circ}$

Question 1:

Write True or False and give reasons for your answer in each of the following:
By geometrical construction, it is possible to divide a line segment in the ratio $\sqrt{3}:\frac{1}{\sqrt{3}}$

Answer: [True]
Solution
We need both positive integers to divide a line segment in the ratio.
So, we can simplify it by multiplying both the terms by .$\sqrt{3}$
We obtain $\sqrt{3}\times \sqrt{3} : \sqrt{3}\times \frac{1}{\sqrt{3}}$
$\Rightarrow 3:1$
So, the required ratio is $3:1$
In geometrical construction is possible to divide a line segment in the ratio $3:1$

Question 2:

Write True or False and give reasons for your answer in each of the following:
To construct a triangle similar to a given $\bigtriangleup ABC$ with its sides $\frac{7}{3}$ of the corresponding sides of $\bigtriangleup ABC$, draw a ray BX making an acute angle with BCand X lies on the opposite side of A concerning BC. The points B₁, B₂,..., B₇ are located at equal distances on BX, B3 is joined to C and then a line segment $B_6{C}'$ is drawn parallel to B₃C where ${C}'$ lies on BC produced. Finally, line segment ${A}'{C}'$ is drawn parallel to AC.

Answer: False
Solution
According to the Question -
To construct a triangle similar to a given $\bigtriangleup ABC$ with its sides $\frac{7}{3}$ of the corresponding sides of $\bigtriangleup ABC$
1. Draw a line segment BC
2. Taking B and C as centres, draw two arcs of suitable radii intersecting each other at A.
3. Join BA and CA?ABC is the required triangle.
4. From B, draw any ray BX downwards, making an acute angle CBX.
5. Locate seven points B₁, B₂, b₃, …. B₇ on BX such that BB₁ = B₁B₂ = B₁B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇.
6. Join B₃C and from B₇ draw a line B₇C’ ? B₃C intersecting the extended line segment BC at C’.
7. From point C’ draw C’A’? CAintersectsg the extended line segment BA at A

But as given, if we join B₃C and from B₆ draw a line B₆C’? B₃C intersecting the extended line segment BC at C’.
$BB_{3}/BB_{6}={BC}/{{BC}'} = 3/6$
${BC}/{{BC}'} = 1/2$
$BC:{BC}'= 1:2$
Hence, the sides are not in the ratio of 7:3
So, the required triangle can not be constructed in this way.
Hence, the given statement is false.

Question 3:

Write True or False and give reasons for your answer in each of the following:
A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of 3 cm from the centre

Answer: [False]
Solution
Radius, r = 3.5 cm
Point distance from centre = 3 cm
But, $r> d\Rightarrow 3.5 cm> 3cm$
So, the point P lies inside the circle.
So, a pair of tangents cannot be drawn to point P to a circle.

Question 4:

Write True or False and give reasons for your answer in each of the following:
A pair of tangents can be constructed to a circle inclined at an angle of $ 170^ 70^{\circ}$.

Answer: [True]
Solution
Tangent: - It is a straight line that touches the curve but does not cross it. A pair of tangents can be constructed to a circle inclined at an angle greater than $0^{\circ}$ but less than $180^{\circ}$. Here, the inclination angle is $170^{\circ}$. Hence, it is possible.

Question 1:

Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio $3:5$.

Solution
Given: AB = 7cm
The required ratio is $3:5$
Let m = 3, n = 5
$m+n= 3+5= 8$

Steps of construction
1. Draw a line segment AB = 7cm.
2. Draw a ray AX making an acute angle with AB
3. Locate 8 points $A_{1},A_{2},A_{3}\cdots A_{8}$ on AX on equidistant. (because $m+n= 8$ )
4. Join $BA_{8}$
5. Through the point $A_{3}$ draw a line parallel to $BA_{8}$ which intersect line AB at P..
Here triangle AA₃P is similar to triangle $AA_{8}B$
$AA_{3}/AA_{8}= AP/AB= 3/5$ (by construction)
Therefore $AP:BP= 3:5$

Question 2:

Draw a right triangle ABC in which BC = 12 cm, AB = 5 cm and $\angle B=90^ {\circ}$.Construct a triangle similar to it and of scale factor $\frac{2}{3}$. Is the new triangle also a right triangle

Solution
Given BC = 12cm, AB = 5 cm, $\angle B= 90^{\circ}$

Steps of construction
1. Draw a line $B C=12 \mathrm{~cm}$
2. From $B$ draw $A B=5 \mathrm{~cm}$ which makes an angle of $90^{\circ}$ at $B$.
3. Join AC
4. Make an acute angle at B as $<C B X$
5. On BX mark 3 points at equal distance $X_1, X_2, X_3$.
6. Join $ X_3C$
7. From $X_2$ draw $X_2 C^{\prime} \| X_3 C$ intersect AB at $C^{\prime}$
8. From point $C^{\prime}$ draw $C^{\prime} A^{\prime} \| C A$ intersect $\mathrm{AB} A^{\prime}$

Now $\triangle A^{\prime} B C^{\prime}$ is the required triangle and $\triangle A^{\prime} B C^{\prime}$ is also a right triangle.

Question 3:

Draw a triangle ABC in which BC = 6 cm, CA = 5 cm, and AB = 4cm. Construct a triangle similar to it and of scale factor$\frac{5}{3}$

Solution
Given : BC = 6cm, CA = 5cm, AB = 4cm
Scale factor = 5/3
Let m = 5 and n = 3

Steps of construction

1. Draw a line BC = 6c cm

2. Taking B and C as centre mark arcs of length 4cm and 5cm respectively,y intersects each other at point A.

3. Join BA and CA

4 . Draw a ray BX making a g acute angle with BC.

5. Locate 5 Points on BX in equidistant positions as B₁, B₂, B₃, B₄, B₅.

6.Join B₃ to C and draw a line through B5 parallel to B₃C to intersect at BC extended at ${C}'$.

7. Draw a line through ${C}'$ parallel to AC intersect AB extended at ${A}'$ .
Now ${A}'B{C}'$ is required triangle.

Question 4:

Construct a tangent to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.

Solution
Given : Radius = 4cm

Steps of construction
1. Draw a circle at radius r = 4 cm at point O.
2. Take a point P at a distance of 6cm from point O and join PO
3. Draw a perpendicular bisector of line PO. M is the midpoint of PO.
4. Taking M as the centre, we draw another circle of radius equal to MO, and it intersects the given circle at points Q and R
5. Now, join PQ and PR.
Then PQ and PR one the required two tangents.

Question 1:

Two line segments AB and AC include an angle of $60^{\circ}$ where AB = 5 cm and AC = 7 cm. Locate points P and Q on AB and AC, respectively,y such that $AP= \frac{3}{4}AB$ and $AQ= \frac{1}{4} AB$. Join P and Q and measure the length of PQ.

Solution
Given :
AB = 5 cm and AC = 7 cm
$AP= \frac{3}{4}AB\: \: \cdots 1$
$AQ= \frac{1}{4}AC\: \: \cdots 2$
From equation 1
$AP= \frac{3}{4}AB$
$AP= \frac{3}{4}\times 5= \frac{15}{4}\: \: \left [ \because AB= 5cm \right ]$
P is any point on B
$\therefore PB= AB-AP= 5-\frac{15}{4}= \frac{20-15}{4}= \frac{5}{4}cm$
$\frac{AP}{AB}= \frac{15}{4}\times \frac{4}{5}= \frac{1}{3}$
$AP:AB= 1:3$
$\therefore$scale of a line segment AB is $\frac{1}{3}$


Steps of construction
1. Draw a line segment AB = 5 cm
2. Now draw ray AO, which makes an angle,
3. Which A as centre and radius equal to 7 cm, draw an arc cutting line AO at C
4. Draw ray AP with an acute angle BAP
5. Along AP make 4 points $A_{1},A_{2},A_{3},A_{4}$ with equal distance.
6. Join $A_{4}B$
7. From $A_{3}$ draw $A_{3}P$ which is parallel to $A_{4}B$ which meet AB at point P.
Then P is a point which divides AB in a ratio 3: 1
AP : PB = 3 : 1
8. Now draw ray AQ, with an acute angle CAQ.
9. Along AQ mark 4 points $B_{1},B_{2},B_{3},B_{4}$ with equal distance.
10. Join $B_{4}C$
11. From $B_{1}$ draw $B_{1}Q$ which is parallel to $B_{4}C$ which meet AC at point Q.
Then Q is a point which divides AC in a ratio 1 : 3
AQ : QC = 1 : 3
12. Finally, you join PQ, and its measurement is 3.25 cm.

Question 2:

Draw a parallelogram ABCD in which BC = 5 cm, AB = 3 cm, and ABC=$60^{\circ}$, and divide it into triangles BCD and ABD by the diagonal BD. Construct the triangle BD'C' similar to DBDC with scale factor $\frac{4}{3}$. Draw the line segment D'A' parallel to DA where A' lies on the extended side BA. Is A'BC'D' a parallelogram?

Solution

Steps of construction
1. Draw, A-line AB = 3 cm
2 Draw a ray by making $\angle ABP= 60^{\circ}$
3. Taking B as the centre and radius equal to 5 cm. Draw an arc which cuts BP at point C
4. Again draw ray AX making $\angle {Q}'AX= 60^{\circ}$
5. With A as the centre and radius equal to 5 cm, draw an arc which cuts AX at point D
6. Join C and D Here ABCD is a parallelogram
7. Join BD , BD is a diagonal of parallelogram ABCD
8. From B draw a ray BQ with any acute angle at po, int B, i.e., $\angle CBQ$ is the acute angle
9. Locate 4 points $B_{1},B_{2},B_{3},B_{4}$ on BQ with equal distance.
10. Join $B_{3}C$ and from $B_{4},{C}'$ parallel to $B_{3}C$ which intersect at point ${C}'$
11. From point ${C}'$ draw line ${C}'{D}'$ which is parallel to CD
12. Now draw a line segment ${D}'{A}'$ parallel to DA
Note : Here ${A}',{C}'$ and ${D}'$ are the extended sides.
13. ${A}'B{C}'{D}'$ is a parallelogram in which ${A}'{D}'= 6\cdot 5\, cm$ and ${A}'{B}= 4\, cm$ and ${A}'B{D}'= 60^{\circ}$ divide it into triangles $B{C}'{D}'$ and ${A}'{BD}'$ by the diagonal ${BD}'$

Question 3:

Draw two concentric circles of radii 3 cm and 5 cm. Taking a point on the outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation.

Solution

Steps of construction
1. Draw two concentric circles with centre O and radii 3 cm and 5 cm
2. Taking any point P on the outer cijoin, join P and O
3. Draw a perpendicular bisector of OP let M be the midpoint of OP
4. Taking M as the centre and OM as the radius, draw a circle which cuts the inner circle at Q and R
5. Join PQ and PR. Thu, PQ and PR are required tangents
On measuring PQ and PR, we find that PQ = PR = 4 cm
Calculations
$\bigtriangleup OQP, \angle OQP= 90^{\circ}$
[usiPythagoras' theorem]
$\left ( 5 \right )^{2}= \left ( 3 \right )^{2}+\left ( PQ \right )^{2}$
$25-9= PQ^{2}$
$16= PQ^{2}$
$\sqrt{16}= PQ$
$4cm= PQ$
H, the length of both tangents is 4 cm.

Question 4

Draw an isosceles triangle ABC in which AB = AC = 6 cm and BC = 5 cm. Construct a triangle PQR similar to ABC in which PQ =8 cm. Also, justify the Construction.

Solution

Steps of construction
1. a Draw a line BC = 5 cm
2. Taking B and C as centres, draw two arcs of equal radius 6 cm intersecting each other at point A.
3. Join AB and AC DABC is required isosceles triangle
4 From B draw ray $B_{X}$ with an acute angle $CB{B}'$
6. draw $B_{1},B_{2},B_{3},B_{4}$ at $BX$ with equal distance
7. Join $B_{3}C$ and from $B_{4}$ draw line $B_{4}D\parallel B_{3}C,$ , intersect extended segment BC at point D.
8. From point D draw $DE\parallel CA$ meting BA produced at E.
Then EBD is required triangle. We can name it PQR.
Justification
$\because B_{4}D\parallel B_{3}C$
$\therefore \frac{BC}{CD}= \frac{3}{1}\Rightarrow \frac{CD}{BC}= \frac{1}{3}$
$Now\, \therefore \frac{BD}{BC}= \frac{BC+CD}{BC}= 1+\frac{CD}{BC}= 1+\frac{1}{3}= \frac{4}{3}$
$Also\, DE\parallel CA$
$\therefore \bigtriangleup ABC\sim \bigtriangleup DBE$
$\frac{EB}{AB}= \frac{DE}{CA}= \frac{BD}{BC}= \frac{4}{3}$

Question 5

Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and $ ABC=60^ {\circ}$.Construct a triangle similar to ABC with scale factor $\frac{5}{7}$. Justify the construction

Solution
Given : AB = 5 cm, BC = 6 cm

Steps of construction

1. Draw a line segment AB = 5 cm

2.draw $< ABO= 60^{\circ}$ B taking as a centre draw an arc of radius BC=6cm

3. Join AC, DABC is the required triangle

4.From point A draw any ray $A{A}'$ with acute angle $\angle BA{A}'$

5.Mark 7 points $B_{1},B_{2},B_{3},B_{4},B_{5},B_{6},B_{7}$ with equal distance.

6.Join $B_{7}B$ and form $B_{5}$ draw $B_{5}X\parallel B_{7}B\, \, BY$making the angle equal From point X draw $XY\parallel BC$ intersecting AC at Y. Then, DAMN is the required triangle whose sides are equal to $\frac{5}{7}$ of the corresponding sides of the $\bigtriangleup ABC.

Justification: Here, $B_{5X}\parallel B_{7}B$ [by construction]
$\therefore \frac{AX}{XB}= \frac{5}{2}\Rightarrow \frac{XB}{AX}= \frac{2}{5}$
Now $\frac{AB}{AX}= \frac{AX+XB}{AX}$
$1+\frac{XB}{AX}= 1+\frac{2}{5}= \frac{7}{5}$
Also, $XY\parallel BC$
$\therefore \bigtriangleup AXY\sim \bigtriangleup ABC$
$\frac{AX}{AB}= \frac{AY}{AC}= \frac{YX}{BC}= \frac{5}{7}$

Question 6

Draw a circle of radius 4 cm. Construct a pair of tangents to it, the angle between which is $60^{\circ}$. Also, justify the
construction. Measure the distance between the centre of the circle and the point of intersection of tangents

Solution

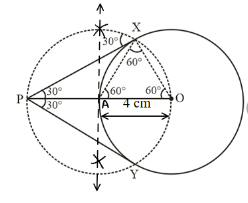
Steps of construction
1. Draw a circle of radius OA = 4 cm with centre O
2. Produce OA to P such that $OA= AP=4 cm$
3. Draw a perpendicular bisector of OP = 8 =8cm
4. Now, taking A as the centre, we draw the circle of radius AP = OA = 4 cm
5Which intersectsst the circle at x and y
6. Join PX and PY
7. PX and PY are the tangents to the circle
Justification
In $\bigtriangleup OAX$ we have
$OA= OP= 4\, cm$ (Radius)
$AX= 4\, cm$ (Radius of circle with centre A)
$\therefore OAX$ is equilateral triangle
$\angle OAX= 60^{\circ}$
$\Rightarrow \angle XAP= 120^{\circ}$
In $\bigtriangleup PAX$ we have
$PA= AX= 4cm$
$\angle XAP= 120^{\circ}$
$\angle APX= 30^{\circ}$
$\Rightarrow APY= 30^{\circ}$
Hence $\angle XPY= 60^{\circ}$

Question 7

Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 9 cm. Construct a triangle similar to $\bigtriangleup ABC$ with scale factor $\frac{3}{2}$ . Justify the construction. Are the two triangles congruent? Note that all three angles and two sides of the two triangles are equal.

Solution

Steps of construction

1 . Draw a line segment BC = 6 cm

2 . Taking B and C as centres, draw an arc of radius AB 4cm and AC = 9 cm

3. Join AB and AC

4 . Triangle ABC is a required triangle. From Bd raw ray BM with acute angle $\angle XBM$

5.Make 3 points $B_{1},B_{2},B_{3}$ on BM with equal distance

6.Join $B_{2}C$ and $B_{3}$ draw $B_{3}X\parallel B_{2}C$ intersecting BC at X From point X draw XY||CA intersecting the extended line segment BA to Y Then $\bigtriangleup BXY$ is the required triangle whose sides are equal to$\frac{3}{2}$ of the $\bigtriangleup ABC$
Justification :
Here $B_{3}X\parallel B_{2}C$
$\therefore \frac{BC}{CX}= \frac{2}{1}$
$\therefore \frac{BX}{BC}= \frac{BC+CX}{BC}= 1+\frac{1}{2}= \frac{3}{2}$
Also $XY\parallel CA$
$\bigtriangleup ABC\sim \bigtriangleup YBX$
$\therefore \frac{YB}{AB}= \frac{YX}{AC}= \frac{BX}{BC}= \frac{3}{2}$.

Here are three angles that are the same, but the three sides are not the same.
$\therefore$The two triangles are not congruent because, if two triangles are congruent, then they have the same shape and size.