• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 9.1 Class 10 Maths Chapter 9 - Some Applications of Trigonometry

NCERT Solutions for Exercise 9.1 Class 10 Maths Chapter 9 - Some Applications of Trigonometry

Edited By Ramraj Saini | Updated on Apr 09, 2024 10:02 AM IST | #CBSE Class 10th
Ongoing Event
CBSE Class 10th  Exam Date : 01 Jan' 2025 - 14 Feb' 2025

NCERT Solutions For Class 10 Maths Chapter 9 Exercise 9.1

NCERT Solutions for Exercise 9.1 Class 10 Maths Chapter 9 Some Applications of Trigonometry are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2024-25. Class 10 maths ex 9.1 deal the application of trigonometry and to be specified, cover all the problems and questions related to height and distances in which we will use trigonometry to find the aspects asked.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 9 Exercise 9.1
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 9 exercise 9.1
  3. Some More Information About NCERT Solutions for Class 10 Maths Exercise 9.1
  4. Benefits of NCERT Solutions for Class 10 Maths Exercise 9.1
  5. NCERT Solutions Subject Wise
  6. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 9.1 Class 10 Maths Chapter 9 - Some Applications of Trigonometry
NCERT Solutions for Exercise 9.1 Class 10 Maths Chapter 9 - Some Applications of Trigonometry

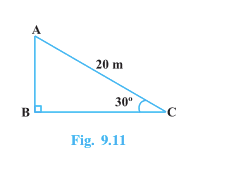
NCERT solutions for exercise 9.1 Class 10 Maths chapter 9 Some Applications of Trigonometry focuses on using trigonometry to find the angle of depression, angle of elevation and line of sight along with this finding the height or length of an object or the distance between two distant objects. 10th class Maths exercise 9.1 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 9 exercise 9.1

Download PDF

Some Applications of Trigonometry Class 10 Chapter 9 Excercise: 9.1

Q1 A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° (see Fig. 9.11).

15942898750991594289872747

Answer:

Given that,
The length of the rope (AC) = 20 m. and \angle ACB =30^o
Let the height of the pole (AB) be h

So, in the right triangle \Delta ABC

sdgfhgjhjfdfg4

By using the Sin rule
\sin \theta = \frac{P}{H} =\frac{AB}{AC}
\sin 30^o =\frac{h}{20}
h =10 m.
Hence the height of the pole is 10 m.

Q2 A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

Answer:

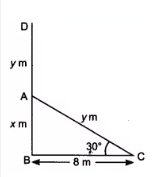
15942915206361594291518564
Suppose DB is a tree and the AD is the broken height of the tree which touches the ground at C.
GIven that,
\angle ACB = 30^o , BC = 8 m
let AB = x m and AD = y m
So, AD+AB = DB = x+y

In right angle triangle \Delta ABC ,
\tan \theta = \frac{P}{B}=\frac{x}{8}
\tan 30^o =\frac{x}{8}=\frac{1}{\sqrt{3}}
So, the value of x = 8/\sqrt{3}

Similarily,
\cos 30^o = \frac{BC}{AC} = \frac{8}{y}
the value of y is 16/\sqrt{3}

So, the total height of the tree is-

x+y=\frac{24}{\sqrt{3}}=8\sqrt{3}

= 8 (1.732) = 13.856 m (approx)

Q3 A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?

Answer:

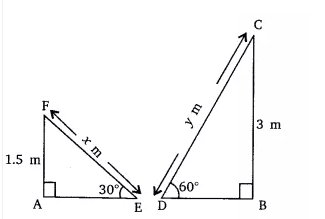
15942902515691594290248488
Suppose x m is the length of slides for children below 5 years and the length of slides for elders children be y m.

Given that,
AF = 1.5 m, BC = 3 m, \angle AEF = 30^o and \angle BDC = 60^o

In triangle \Delta EAF,
\sin \theta = \frac{AF}{EF} = \frac{1.5}{x}
\sin 30^o = \frac{1.5}{x}
The value of x is 3 m.

Similarily in \Delta CDB,
\sin 60^o = \frac{3}{y}
\frac{\sqrt{3}}{2}= \frac{3}{y}
the value of y is 2\sqrt{3} = 2(1.732) = 3.468

Hence the length of the slide for children below 5 yrs. is 3 m and for the elder children is 3.468 m.

Q4 The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.

Answer:

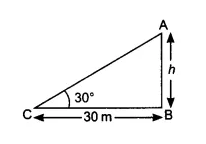
15942902793611594290278112
Let the height of the tower AB is h and the angle of elevation from the ground at point C is \angle ACB = 30^o
According to question,
In the right triangle \Delta ABC ,
\tan \theta = \frac{AB}{BC} = \frac{h}{30}
\tan 30^o =\frac{1}{\sqrt{3}}=\frac{h}{30}
the value of h is 10\sqrt{3} = 10(1.732) = 17.32 m
Thus the height of the tower is 17.32 m

Q5 A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

Answer:

A
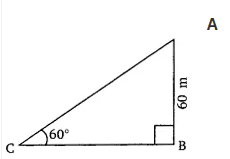
15942903087441594290307251
Given that,
The length of AB = 60 m and the inclination of the string with the ground at point C is \angle ACB = 60^o .
Let the length of the string AC be l .
According to question,
In right triangle \Delta CBA,
\sin 60^{o} = \frac{AB}{AC} = \frac{60}{l}
\frac{\sqrt{3}}{2} = \frac{60}{l}
The value of length of the string ( l ) is 40\sqrt{3} = 40(1.732) = 69.28 m
Hence the length of the string is 69.28 m.

Q6 A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

Answer:

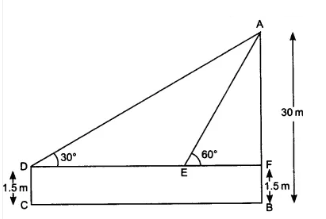
15942903319101594290329650
Given that,
The height of the tallboy (DC) is 1.5 m and the height of the building (AB) is 30 m.
\angle ADF = 30^o and \angle AEF = 60^o

According to question,
In right triangle AFD,
\\\Rightarrow \tan 30^o=\frac{AF}{DF} = \frac{28.5}{DF}\\\\\Rightarrow \frac{1}{\sqrt{3}} = \frac{28.5}{DF}
So, DF = (28.5)\sqrt{3}

In right angle triangle \Delta AFE ,
\tan 60^o =\frac{AF}{FE}=\frac{28.5}{EF}
\sqrt{3}=\frac{28.5}{EF}
EF = 9.5\sqrt{3}

So, distance walked by the boy towards the building = DF - EF = 19\sqrt{3}

Q7 From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.

Answer:

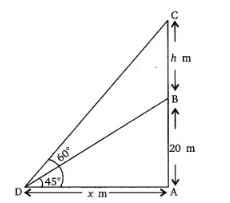
15942903511781594290349905
Suppose BC = h is the height of transmission tower and the AB be the height of the building and AD is the distance between the building and the observer point (D).
We have,
AB = 20 m, BC = h m and AD = x m
\angle CDA = 60^o and \angle BDA = 45^o

According to question,
In triangle \Delta BDA,
\tan 45^o = \frac{AB}{AD}=\frac{20}{x}
So, x = 20 m

Again,
In triangle \Delta CAD,

\\\Rightarrow \tan 60^o = \frac{AB+BC}{AD}=\frac{20+h}{20}\\\\\Rightarrow \sqrt{3}= 1+\frac{h}{20}\\\\\Rightarrow h=20(\sqrt{3}-1)\\\\\Rightarrow 20(0.732) = 14.64 m

Answer- the height of the tower is 14.64 m

Q8 A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.

Answer:

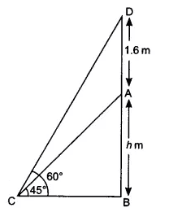
15942903734641594290372019
Let the height of the pedestal be h m. and the height of the statue is 1.6 m.
the angle of elevation of the top of the statue and top of the pedestal is( \angle DCB= 60^o )and( \angle ACB= 45^o ) respectively.

Now,
In triangle \Delta ABC ,
\tan 45^o =1 =\frac{AB}{BC}=\frac{h}{BC}
therefore, BC = h m

In triangle \Delta CBD ,
\\\Rightarrow \tan 60^o = \frac{BD}{BC}=\frac{h+1.6}{h}\\\\\Rightarrow \sqrt{3}= 1+\frac{1.6}{h}
the value of h is 0.8(\sqrt{3}+1) m
Hence the height of the pedestal is 0.8(\sqrt{3}+1) m

Q9 The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.

Answer:

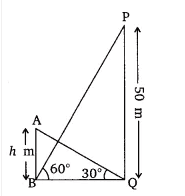
15942904215031594290420227
It is given that, the height of the tower (AB) is 50 m. \angle AQB = 30^o and \angle PBQ = 60^o
Let the height of the building be h m

According to question,
In triangle PBQ,
\tan 60^o = \frac{PQ}{BQ} = \frac{50}{BQ}
\\\sqrt{3} = \frac{50}{BQ}\\ BQ = \frac{50}{\sqrt{3}} .......................(i)

In triangle ABQ,

\tan 30^o = \frac{h}{BQ}
{BQ}=h\sqrt{3} .........................(ii)
On equating the eq(i) and (ii) we get,

\frac{50}{\sqrt{3}}=h\sqrt{3}
therefore, h = 50/3 = 16.66 m = height of the building.

Q10 Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

Answer:

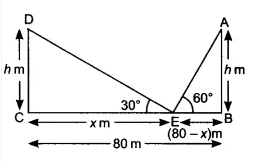
15942904402531594290438964
Given that,
The height of both poles are equal DC = AB. The angle of elevation of of the top of the poles are \angle DEC=30^o and \angle AEB=60^o resp.
Let the height of the poles be h m and CE = x and BE = 80 - x

According to question,
In triangle DEC,

\\\Rightarrow \tan 30^o = \frac{DC}{CE} = \frac{h}{x}\\\\\Rightarrow \frac{1}{\sqrt{3}}= \frac{h}{x}\\\\\Rightarrow x=h\sqrt{3} ..............(i)

In triangle AEB,
\\\Rightarrow \tan 60^o = \frac{AB}{BE}=\frac{h}{80-x}\\\\\Rightarrow \sqrt{3}=\frac{h}{80-x}\\\\\Rightarrow x=80 - \frac{h}{\sqrt{3}} ..................(ii)
On equating eq (i) and eq (ii), we get

\sqrt{3}h=80 - \frac{h}{\sqrt{3}}
\frac{h}{\sqrt{3}}=20
h=20\sqrt{3} m
So, x = 60 m

Hence the height of both poles is ( h=20\sqrt{3} )m and the position of the point is at 60 m from the pole CD and 20 m from the pole AB.

Q11 A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.

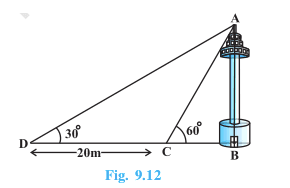
15942904616351594290459973

Answer:

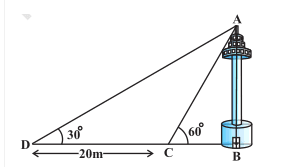
15942904764911594290475054
Suppose the h is the height of the tower AB and BC = x m
It is given that, the width of CD is 20 m,
According to question,

In triangle \Delta ADB ,
\\\Rightarrow \tan 30^o = \frac{AB}{20+x}=\frac{h}{20+x}\\\\\Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{20+x}\\\\\Rightarrow 20+x = h\sqrt{3}\\\\\Rightarrow x = h\sqrt{3}-20 ............(i)

In triangle ACB,
\\\Rightarrow \tan 60^o = \frac{h}{x}=\sqrt{3}\\\\\Rightarrow x= \frac{h}{\sqrt{3}} .............(ii)

On equating eq (i) and (ii) we get:

h\sqrt{3}-20= \frac{h}{\sqrt{3}}
from here we can calculate the value of h=10\sqrt{3}= 10 (1.732) = 17.32\: m and the width of the canal is 10 m.

Q12 From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.

Answer:

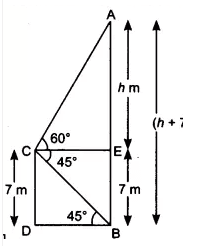
15942904947031594290493105
Let the height of the cable tower be (AB = h+7 )m
Given,
The height of the building is 7 m and angle of elevation of the top of the tower \angle ACE = 60^o , angle of depression of its foot \angle BCE = 45^o .

According to question,

In triangle \Delta DBC ,
\\\tan 45^o = \frac{CD}{BD} = \frac{7}{BD} = 1\\ BD =7\ m
since DB = CE = 7 m

In triangle \Delta ACE ,

\\\tan 60^o = \frac{h}{CE}=\frac{h}{7}=\sqrt{3}\\ \therefore h = 7\sqrt{3}\ m

Thus, the total height of the tower equal to h+7 =7(1+\sqrt{3}\) m

Q13 As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.

Answer:

Given that,
The height of the lighthouse (AB) is 75 m from the sea level. And the angle of depression of two different ships are \angle ADB = 30^0 and \angle ACB = 45^0 respectively
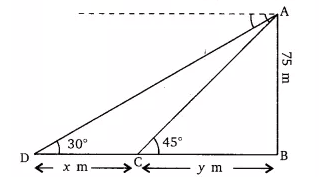
15942905447991594290543400
Let the distance between both the ships be x m.
According to question,

In triangle \Delta ADB ,

\tan 30^0 = \frac{AB}{BD}=\frac{75}{x+y} = \frac{1}{\sqrt{3}}
\therefore x+y = 75 \sqrt{3} .............(i)

In triangle \Delta ACB ,

\tan 45^0 = 1 =\frac{75}{BC}=\frac{75}{y}
\therefore y =75\ m .............(ii)

From equation (i) and (ii) we get;
x = 75(\sqrt{3}-1)=75(0.732)
x = 54.9\simeq 55\ m

Hence, the distance between the two ships is approx 55 m.

Q14 A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see Fig. 9.13). Find the distance traveled by the balloon during the interval.

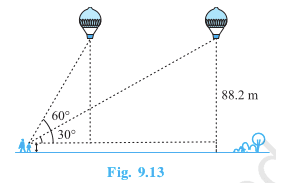
15942906011101594290599656

Answer:

Given that,
The height of the girl is 1.2 m. The height of the balloon from the ground is 88.2 m and the angle of elevation of the balloon from the eye of the girl at any instant is ( \angle ACB =60^0 ) and after some time \angle DCE =30^0 .
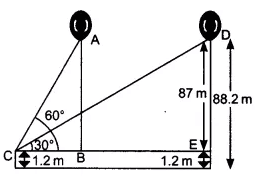
15942906424181594290640376
Let the x distance travelled by the balloon from position A to position D during the interval.
AB = ED = 88.2 - 1.2 =87 m

Now, In triangle \Delta BCA ,

\\\tan 60^0 = \sqrt{3}=\frac{AB}{BC}=\frac{87}{BC}\\ \therefore BC = 29\sqrt{3}

In triangle \Delta DCE ,

\\\tan 30^0 = \frac{1}{\sqrt{3}}=\frac{DE}{CE}=\frac{87}{CE}\\ \therefore CE = 87\sqrt{3}

Thus, distance traveled by the balloon from position A to D

= CE - BC =87\sqrt{3}-29\sqrt{3} = 58\sqrt{3} m

Q15 A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.

Answer:

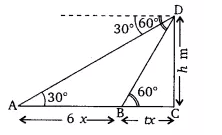
15942906686221594290666652
Let h be the height of the tower (DC) and the speed of the car be x\ ms^{-1} . Therefore, the distance (AB)covered by the car in 6 seconds is 6 x m. Let t time required to reach the foot of the tower. So, BC = x t

According to question,
In triangle \Delta DAC ,
\\\tan 30^0 = \frac{1}{\sqrt{3}}=\frac{h}{6x+xt}\\ x(6+t) = h\sqrt{3} ..........................(i)

In triangle \Delta BCD ,

\\\tan 60^0 = \sqrt{3} = \frac{h}{xt}\\ \therefore h = 3.xt ...................(ii)

Put the value of h in equation (i) we get,
\\x(6+t) = (\sqrt{3}.\sqrt{3})xt\\ 6x +xt = 3xt\\ 6x = 2xt
t = 3

Hence, from point B car take 3 sec to reach the foot of the tower.

Q16 The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.

Answer:

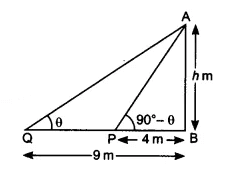
15942906874451594290685895
Let the height of the tower be h m.
we have PB = 4m and QB = 9 m
Suppose \angle BQA = \theta , so \angle APB =90- \theta

According to question,

In triangle \Delta ABQ ,

\\\tan \theta = \frac{h}{9}\\ \therefore h = 9 \tan \theta ..............(i)

In triangle \Delta ABP ,

\\\tan (90-\theta)=\cot \theta = \frac{h}{4}\\ \therefore h = 4\cot \theta .....................(ii)

multiply the equation (i) and (ii), we get

\\h^2 = 36\\ \Rightarrow h = 6 m

Hence the height of the tower is 6 m.

Some More Information About NCERT Solutions for Class 10 Maths Exercise 9.1

NCERT syllabus Class 10 Maths chapter 9 exercise 1: The questions in exercise 9.1 Class 10 Maths, broadly consist of some basic questions in which we have to find height and distance with the help of the formula of tangent, cosine and sine. NCERT solutions for NCERT book Class 10 Maths exercise 9.1 also consist of questions that are a little bit harder as we have to apply the trigonometric formula twice and also use some basic phenomena of real life such as the shadow of objects. Exercise 9.1 Class 10 Maths covers all types of questions that can be formed height and distance. Students can find here Some applications of Trigonometry Class 10 Notes that are very helpful in quickly revising all important concepts discussed in this chapter.

Benefits of NCERT Solutions for Class 10 Maths Exercise 9.1

  • Class 10 Maths chapter 9 exercise 9.1 broadly covers a few topics of height and distance using trigonometry
  • There are the various questions that are picked from the topics of NCERT Class 10 Maths chapter 9 exercise 9.1 in competitive exams like Joint Entrance Exam (JEE Main).
  • Exercise 9.1 Class 10 Maths can be the basis for Class 12 chapter 10 vector algebra and chapter 11 three dimensional geometry
Pearson | PTE

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

Apply

Also see-

CBSE Class 10 Sample Papers
CBSE Class 10 Sample Papers
Download Now

NCERT Solutions Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. According to NCERT solutions for Class 10 Maths 9 exercise 9.1 what do you mean by trigonometric ratio.

 The values of all trigonometric functions dependent on the value of the ratio of sides in a right-angled triangle are known as trigonometric ratios.

2. How many topic are covered in NCERT solutions for Class 10 Maths 9 exercise 9.1?

  • angle of depression 

  • angle of elevation 

  • line of sight

  • finding the height or length of an object or the distance between two distant objects

3. What do you mean by angle of elevation according to NCERT solutions for Class 10 Maths 9 exercise 9.1?

The angle created by the line of sight with the horizontal when it is above the horizontal level is the angle of elevation of an item that we can see.

When we elevate our head to gaze at an object, for example.

4. According to NCERT answers for Class 10 Maths 9 exercise 9.1, what do you mean by angle of elevation?

The angle formed by the line of sight with the horizontal when it is below the horizontal level is the angle of depression of an item that we can see.

When we drop our head to gaze at an object, for example.

5. What do you mean by line of sight according to NCERT solutions for Class 10 Maths 9 exercise 9.1?

The line of sight is the line which is a line traced from an observer's eye to a point in the item being seen.

6. An object's height or length, as well as the distance between two distant objects, may be calculated using.

Trigonometric ratios can be used to calculate an object's height or length, as well as the distance between two distant objects.

7. What is the total number of solved examples prior to the Class 10 Maths exercise 9.1?

Before the Class 10 Mathematics chapter 9 activity 9.1, there are seven key questions that must be answered.

8. In the NCERT solutions for Class 10 Maths chapter 9 exercise, how many questions are there?

In the NCERT solutions for the Class 10 Maths chapter 9 exercise, there are 16 problems.

Also Read

Articles

Upcoming School Exams

National Means Cum-Merit Scholarship

Application Date:17 December,2024 - 20 February,2025

Bihar Open Board 10th Examination

Application Date:18 December,2024 - 30 January,2025

Bihar Open Board 12th Examination

Application Date:18 December,2024 - 30 January,2025

Manipur Board 12th Examination

Admit Card Date:30 December,2024 - 26 March,2025

Central Board of Secondary Education Class 10th Examination

Exam Date:01 January,2025 - 14 February,2025

View All School Exams

Certifications By Top Providers

Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD
LOR Full Form in Education - Letter of Recommendation
5 min ⋆ Oct 24, 2024 11:10 AM IST
Top 10 Easiest Countries To Go To Study Abroad In 2025
7 min ⋆ Dec 31, 2024 10:12 AM IST
Magister Jurisdiction
4 min ⋆ Mar 18, 2023 16:03 PM IST
Cheapest and Affordable Universities in Ireland in 2025
15 min ⋆ Dec 31, 2024 03:12 AM IST
GMAT Exam Dates 2025: City Wise Test Schedule in India
13 min ⋆ Dec 31, 2024 03:12 AM IST
Letter of Recommendation: How to Write LOR, Samples and Format
9 min ⋆ Dec 31, 2024 03:12 AM IST

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
can we apply for diploma if we have passed 10th cbse lo

Yes, you can definitely apply for diploma courses after passing 10th CBSE. In fact, there are many diploma programs designed specifically for students who have completed their 10th grade.

Generally, passing 10th CBSE with a minimum percentage (often 50%) is the basic eligibility for diploma courses. Some institutes might have specific subject requirements depending on the diploma specialization.

There is a wide range of diploma courses available in various fields like engineering (e.g., mechanical, civil, computer science), computer applications, animation, fashion design, hospitality management, and many more.

You can pursue diplomas at various institutions like:


Read Complete Answer
Nitin Kumar 14 June,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Trusted by 3,500+ universities and colleges globally | Accepted for migration visa applications to AUS, CAN, New Zealand , and the UK

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Board Exams Date Sheet 2025 Live: RBSE 10th, 12th exams from March 6; CBSE admit card expected by month-end
January 14, 2025 - 11:09 AM IST
Board Exam Date 2025 Live: Bihar Class 10, 12 model papers out, time table soon; updates on CBSE, UP
December 06, 2024 - 10:42 PM IST
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST

Stay up-to date with CBSE Class 10th News

Back to top