NCERT Solutions For Class 10 Science Chapter 11 Electricity

Q.2 Define the unit of currcurrent ent.

Answer:

Ampere(A) is a unit of current. 1A is the flow of 1C of charge through a wire in 1s of time.

current $I=\frac{q}{t}$

$
1 A=\frac{1 C}{1 \sec }
$

Q.3 Calculate the number of electrons constituting one coulomb of charge.

Answer:

Given: Q=1C

We know that the charge of an electron $e=1.6 \times 10^{-19} \mathrm{C}$

$
\begin{aligned}
& Q=n e \\
& \Rightarrow n=\frac{Q}{e} \\
& \Rightarrow n=\frac{1}{1.6 \times 10^{-19}}=6.25 \times 10^{18}
\end{aligned}
$

Thus, the number of electrons constituting one coulomb of charge is $6 \times 10^{18}$ electrons.

Class 10 science Chapter 11 ncert Solutions - Topic 11.2

Q.1 Name a device that helps to maintain a potential difference across a conductor.

Answer:

A battery, cell or power supply source helps to maintain a potential difference across a conductor.

Q.2 What is meant by saying that the potential difference between two points is 1 V?

Answer:

The potential difference between two points is 1 V means 1 J of work is required to move a charge of 1C from one point to another.

Q.3 How much energy is given to each coulomb of charge passing through a 6 V battery?

Answer:

Given: potential difference = 6V and charge =1C.

$
\begin{aligned}
& \text { Potential difference }=\frac{\text { work done }}{\text { charge }} \\
& \Rightarrow 6=\frac{\text { work done }}{1} \\
& \Rightarrow \text { work done }=6 \times 1=6 \mathrm{~J}
\end{aligned}
$

Thus, 6J energy is given to each coulomb of charge passing through a 6V battery.

NCERT solutions for class 10 science chapter 11 Electricity: Topic 11.5

Q.1 On what factors does the resistance of a conductor depend?

Answer:

The resistance of a conductor depends on :

1. Cross-section area of the conductor.

2. Length of conductor

3. The temperature of the conductor.

4. Nature of the material of the conductor.

Q.2 Will current flow more easily through a thick wire or a thin wire of the same material, when connected to the same source? Why?

Answer:

We know that resistance is given as

$
R=\frac{\rho l}{A}
$remain

$\mathrm{R}=$ resistance
$\rho=$ resistivity
$l$=length of wire
$A=$ area of cross-section
Resistance is inversely proportional to the area of the cross-section.
The thicker the wire, the more cross-sectional area, resulting in less resistance, resulting in more current flow.

Q.3 Let the resistance of an electrical component remain constant while the potential difference across the two ends of the component decreases to half of its former value. What change will occur in the current through it?

Answer:

By Ohm's law,

$
\begin{aligned}
& \mathrm{V}=\mathrm{IR} \\
& I=\frac{V}{R}
\end{aligned}
$

$\mathrm{V}=$ potential difference
I =current
$\mathrm{R}=$ resistance
Now, the potential difference is reduced to half i.e.

$
V^{\prime}=\frac{V}{2}
$

$\mathrm{R}^{\prime}=\mathrm{R}=$ resistance
I' =current

$
I^{\prime}=\frac{\frac{V}{2}}{R}=\frac{V}{2 R}=\frac{I}{2}
$

Q.4 Why are coils of electric toasters and electric irons made of an alloy rather than a pure metal?

Answer:

The resistivity of an alloy is higher than pure metal, so the alloy does not melt at high temperatures. Thus, coils of electric toasters and electric irons are made of an alloy rather than a pure metal.

Q.5 Use the data in the Table to answer the following –

(a) Which among iron and mercury is a better conductor?
(b) Which material is the best conductor?

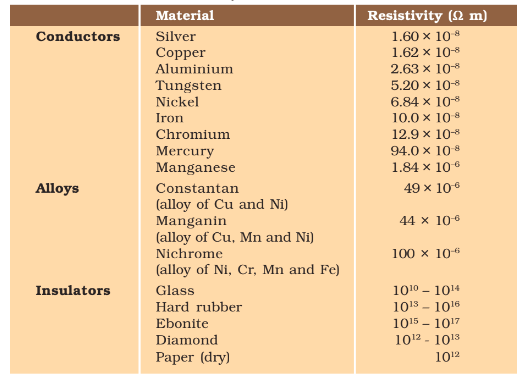
Answer:

The lower the value of resistivity, the lower is the resistance for a material of given area and length. If resistance is low, current flow will be high when a potential difference is applied across the conductor.

(a) resistivity of iron $=10.0 \times 10^{-8} \Omega \mathrm{~m}$
the resistivity of mercury $=94 \times 10^{-8} \Omega \mathrm{~m}$
The resistivity of mercury is more than iron, so iron is a better conductor than mercury.

(b) From the table, we can observe that silver has the lowest resistivity, so it is the best conductor.

NCERT solutions for class 10 science chapter 11 Electricity: Topic 11.6

Q.1 Draw a schematic diagram of a circuit consisting of a battery of three cells of 2 V each, a $5 \Omega$ resistor, an $8 \Omega$ resistor, a $12 \Omega$ resistor, and a plug key, all connected in series.

Answer:

The schematic diagram of a circuit consisting of a battery of three cells of 2 V each, a $5 \Omega$ resistor, an $8 \Omega$ resistor, and a $12 \Omega$ resistor, and a plug key, all connected in series, is as shown below :

Q.2 Redraw the circuit of Question 1, putting in an ammeter to measure the current through the resistors and a voltmeter to measure the potential difference across the $12 \Omega$ resistor. What would be the readings in the ammeter and the voltmeter?

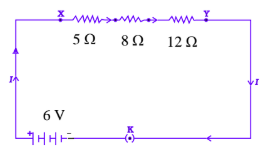
Answer:

The diagram is as shown :

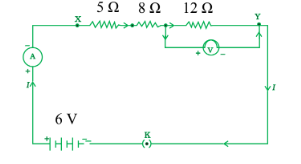
Resistance of circuit, R=5+8+12=25

Potential = 6V

$
\begin{aligned}
& V=I R \\
& \Rightarrow I=\frac{V}{R}=\frac{6}{25}=0.24 \mathrm{~A}
\end{aligned}
$

Now, for a 12 ohm resistor, current $=0.24 \mathrm{~A}$.
By Ohm's law,

$
V=I R=0.24 \times 12=2.88 \mathrm{~V}
$

The reading of the ammeter is 0.24 A, and the voltmeter is 2.88 V.

NCERT solutions for class 10 science chapter 11 Electricity Topic 11.6

Q.1 Judge the equivalent resistance when the following are connected in parallel (a) $1 \Omega$ and $10^6 \Omega$, (b) $1 \Omega$ and $10^3 \Omega$, and $10^6 \Omega$

Answer:
(a) $1 \Omega$ and $10^6 \Omega$
$R=$ Equivalent resistance

$
\begin{aligned}
& \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2} \\
& \Rightarrow \frac{1}{R}=\frac{1}{1}+\frac{1}{10^6} \\
& \Rightarrow \frac{1}{R}=\frac{10^6+1}{10^6} \\
& \Rightarrow R=\frac{10^6}{10^6+1} \approx 1 \Omega
\end{aligned}
$

(b) $1 \Omega$ and $10^3 \Omega$, and $10^6 \Omega$,
$\mathrm{R}=$ Equivalent resistance

$
\frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}
$

$\begin{aligned} & \Rightarrow \frac{1}{R}=\frac{1}{1}+\frac{1}{10^3}+\frac{1}{10^6} \\ & \Rightarrow \frac{1}{R}=\frac{10^6+10^3+1}{10^6} \\ & \Rightarrow R=\frac{10^6}{10^6+10^3+1}=0.999 \Omega \approx 1 \Omega\end{aligned}$

Q.2 An electric lamp of $100 \Omega$, a toaster of resistance $50 \Omega$ and a water filter of resistance $500 \Omega$ are connected in parallel to a 220 V source. What is the resistance of an electric iron connected to the same source that takes as much current as all three appliances, and what is the current through it?

Answer:

Given : $R_1=100 \Omega, R_2=50 \Omega, R_3=500 \Omega$
$\mathrm{R}=$ Equivalent resistance

$
\begin{aligned}
& \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \\
& \Rightarrow \frac{1}{R}=\frac{1}{100}+\frac{1}{50}+\frac{1}{500} \\
& \Rightarrow \frac{1}{R}=\frac{5+10+1}{500}=\frac{16}{500} \\
& \Rightarrow R=\frac{500}{16}=31.25 \Omega
\end{aligned}
$

By Ohm's law,

$
I=\frac{V}{R}=\frac{220}{31.25}=7.04 A
$

Hence, the resistance of the electric iron is 31.25, and the current through it is 7.04 A.

Q.3 What are the advantages of connecting electrical devices in parallel with the battery instead of connecting them in series?

Answer:

In parallel, there is no division of voltage among the appliances, so the potential difference across all appliances is equal, and the total effective resistance of a circuit can be reduced. Hence, connecting electrical devices in parallel with the battery is beneficial instead of connecting them in series.

Q.4 How can three resistors of resistances $2 \Omega, 3 \Omega$, and $6 \Omega$ be connected to give a total resistance of (a) $4 \Omega,(b) 1 \Omega$?

Answer:
(a) $R_1=3, R_2=6, R_3=2$
$\mathrm{R}=$ Equivalent resistance

$
\begin{aligned}
& \frac{1}{R_{12}}=\frac{1}{R_1}+\frac{1}{R_2} \\
& \Rightarrow \frac{1}{R_{12}}=\frac{1}{3}+\frac{1}{6} \\
& \Rightarrow \frac{1}{R_{12}}=\frac{2+1}{6} \\
& \Rightarrow R_{12}=\frac{6}{3}=2 \\
& R=R_{12}+R_3=2+2=4
\end{aligned}
$

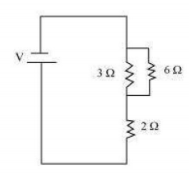
(b) 1 Ohm

R=Equivalent resistance

Connect all three resistors in parallel

$\begin{aligned} \frac{1}{R}= & \frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \\ & \Rightarrow \frac{1}{R}=\frac{1}{2}+\frac{1}{3}+\frac{1}{6} \\ & \Rightarrow \frac{1}{R}=\frac{6+3+1}{6} \\ & \Rightarrow R=\frac{16}{6}=1 \Omega\end{aligned}$

Q.5 (a) What is the highest total resistance that can be secured by combinations of four coils of resistance $4 \Omega, 8 \Omega, 12 \Omega, 24 \Omega ?$

Answer:

The highest total resistance is obtained when all the resistors are connected in a series

$4+8+12+24=48 \Omega$

Q.5 (b) What is the lowest total resistance that can be secured by combinations of four coils of resistance $4 \Omega, 8 \Omega, 12 \Omega, 24 \Omega ?$

Answer:

The lowest total resistance is R, is obtained when all the resistors are connected in parallel.

$\begin{aligned} & \frac{1}{R}=\frac{1}{4}+\frac{1}{8}+\frac{1}{12}+\frac{1}{24} \\ & \frac{1}{R}=\frac{6+3+2+1}{24}=\frac{12}{24} \\ & R=\frac{24}{12}=2\end{aligned}$

NCERT solutions for class 10 science chapter 11 Electricity topic 11.6

Q. 1. Why does the cord of an electric heater not glow while the heating element does?

Answer:

The heating element of an electric heater is a resistor.

The amount of heat production is given as $H=I^2 R t$.

The resistance of elements (alloys) of an electric heater is high. As current flows through this element, it becomes hot and glows red.

The resistance of the cord (metal like Cu or Al)of an electric heater is low. As current flows through this element, it does not become hot and does not glow red.

Q. 2. Compute the heat generated while transferring 96000 coulomb of charge in one hour through a potential difference of 50 V.

Answer:

Given: potential difference = 50 V.

Charge = 9600 C

time = 1 hr=3600 s

$\begin{aligned} & \quad I=\frac{\text { charge }}{\text { time }(\text { seconds })}=\frac{9600}{3600}=\frac{80}{3} \mathrm{~A} \\ & \text { So, } H=\text { VIt } \\ & \Rightarrow H=50 \times \frac{80}{3} \times 3600 \\ & \Rightarrow H=4800000 \mathrm{~J}=4.8 \times 10^6 \mathrm{~J}\end{aligned}$

Q. 3 An electric iron of resistance $20 \Omega$ takes a current of 5 A. Calculate the heat developed in 30 s.

Answer:

Given : resistance $=\mathrm{R}=20 \Omega$, Time $=30$ s, current $=\mathrm{I}=5 \mathrm{~A}$

$
\begin{aligned}
& V=I R \\
& \Rightarrow V=5 \times 20=100 \mathrm{~V} \\
& \\
& \quad H=V I t \\
& \quad \Rightarrow H=100 \times 5 \times 30 \\
& \quad \Rightarrow H=15000 \mathrm{~J}=1.5 \times 10^4 \mathrm{~J}
\end{aligned}
$

NCERT solutions for class 10 science chapter 11 Electricity topic 11.8

Q.1 What determines the rate at which energy is delivered by a current?

Answer:

The rate at which energy is delivered by a current is power.

Power P=I² R, where I is the current and R is the resistance of the circuit/ appliance. Power depends on the current drawn by the appliance and the resistance of the appliance.

Q.2 An electric motor takes 5 A from a 220 V line. Determine the power of the motor and the energy consumed in 2 h.

Answer:

Given: I= 5 A and V= 220 V.

Power=P=VI

$P=220 \times 5=1100 \mathrm{~W}$
Time $=2 h r=2 \times 60 \times 60=7200 s$
The energy consumed $=$ power $\times$ time$=1100 \times 7200 \mathrm{~J}=7920000 \mathrm{~J}$
Power of motor $=1100 \mathrm{~W}$
Energy consumed by motor $=7920000 \mathrm{~J}$

Q. 2. Which of the following terms does not represent electrical power in a circuit?

(a) $I^2 R(b) I R^2(c) V I(d) V^2 / R$

Answer:
We know that power $=\mathrm{P}=\mathrm{VI}$-------------- (1)

Put, $\mathrm{V}=\mathrm{IR}$ in equation 1

$
P=I^2 R
$

Pur, $I=\frac{V}{R}$ in equation 1 ,

$
P=V \times \frac{V}{R}=\frac{V^2}{R}
$

$\mathrm{P}=$ power, $\mathrm{V}=$ potencial difference, $\mathrm{I}=$ current, $\mathrm{R}=$ resistance
P cannot be $I R^2$.

Thus, option b is correct.

Q. 3. An electric bulb is rated 220 V and 100 W. When it is operated on 110 V, the power consumed will be

(a) 100 W (b) 75 W (c) 50 W (d) 25 W

Answer:

Given : $\mathrm{V}=220 \mathrm{~V}, \mathrm{P}=100 \mathrm{~W}$

$
P=\frac{V^2}{R}
$

The resistance of the bulb

$
\Rightarrow R=\frac{V^2}{P}=\frac{(220)^2}{100}=484 \Omega
$

If the bulb is operated on 110 V andthe resistance is the same, the power consumed will be $\mathrm{P}^{\prime}$

$
P^{\prime}=\frac{V^2}{R}=\frac{(110)^2}{484}=25 W
$

Hence, option d is correct.

Q. 4. Two conducting wires of the same material and of equal lengths and equal diameters are first connected in series and then parallel in a circuit across the same potential difference. The ratio of heat produced in series and parallel combinations would be

(a) 1:2 (b) 2:1 (c) 1:4 (d) 4:1

Answer:

If resistors are connected in parallel, the net resistance is given as

$
\begin{aligned}
& \frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2} \\
& \Rightarrow \frac{1}{R_p}=\frac{1}{R}+\frac{1}{R} \\
& \Rightarrow \frac{1}{R_p}=\frac{2}{R} \\
& \Rightarrow R_p=\frac{R}{2}
\end{aligned}
$

If resistors are connected in series, the net resistance is given as

$
\Rightarrow R_s=R_1+R_2=R+R=2 R
$

Heat produced $=\mathrm{H}=\frac{V^2}{R} t$

$
\begin{aligned}
& \frac{H_s}{H_p}=\frac{\frac{V^2 t}{2 R}}{\frac{V^{2 t}}{\frac{R}{2}}} \\
& \Rightarrow \frac{H_s}{H_p}=\frac{1}{4} \\
& \Rightarrow H_s: H_p=1: 4
\end{aligned}
$

Thus, option c is correct.

Q. 5. How is a voltmeter connected in the circuit to measure the potential difference between two points?

Answer:

A voltmeter should be connected in parallel to measure the potential difference between two points.

Q. 6. A copper wire has a diameter of 0.5 mm and resistivity of $1.6 \times 10^{-8} \Omega$ m. What will be the length of this wire to make its resistance $10 \Omega$? How much does the resistance change if the diameter is doubled?

Answer:

Given : diameter $=\mathrm{d}=0.5 \mathrm{~mm}$ and resistivity $=\rho=1.6 \times 10^{-8} \Omega \mathrm{~m}$, resistance $=\mathrm{R}=10 \Omega$
Area $=A$

$
\begin{aligned}
& A=\frac{\pi d^2}{4}=\frac{3.14 \times 0.5 \times 0.5}{4} \\
& \Rightarrow A=0.000000019625 \mathrm{~m}^2
\end{aligned}
$

We know

$
\begin{aligned}
& R=\frac{\rho l}{A} \\
& \Rightarrow l=\frac{R A}{\rho}=\frac{10 \times 0.000000019625}{1.6 \times 10^{-8}} \\
& =122.72 \mathrm{~m}
\end{aligned}
$

If the diameter is doubled.

$
\mathrm{d}=1 \mathrm{~mm}
$

Area $=A^{\prime}$

$
\begin{aligned}
& A^{\prime}=\frac{\pi d^2}{4}=\frac{3.14 \times 1 \times 1}{4} \\
& \Rightarrow A=0.000000785 \mathrm{~m}^2
\end{aligned}
$

We know

$
\begin{aligned}
& R^{\prime}=\frac{\rho l}{A^{\prime}} \\
& \Rightarrow R^{\prime}=\frac{1.6 \times 10^{-8} \times 122.72}{0.000000785} \\
& \Rightarrow R^{\prime}=2.5 \Omega \\
& \frac{R^{\prime}}{R}=\frac{2.5}{10}=\frac{1}{4}
\end{aligned}
$

Hence, new resistance is $\frac{1}{4}$ of original resistance.

Q. 7. The values of current I flowing in a given resistor for the corresponding values of potential difference V across the resistor are given below –

I (amperes) 0.5 1.0 2.0 3.0 4.0
V (volts) 1.6 3.4 6.7 10.2 13.2

Plot a graph between V and I and calculate the resistance of that resistor

Answer:

The plot between voltage and current is as shown :

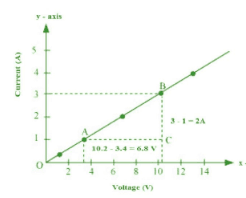
The slope of the line gives resistance (R)

$R=\frac{6.8}{2}=3.4 \Omega$

Q.8. When a 12 V battery is connected across an unknown resistor, there is a current of 2.5 mA in the circuit. Find the value of the resistance of the resistor.

Answer:

Given : V=12V , I = 2.5 mA = 0.0025 A

$R=\frac{12}{0.0025}=4800 \Omega=4.8 k \Omega$

Q.9. A battery of 9 V is connected in series with resistors of $02 \Omega$ , $0.3 \Omega$ , $0.4 \Omega$ , $0.5 \Omega$ and $12 \Omega$ respectively. How much current would flow through the $12 \Omega$ resistor?

Answer: Total resistance $=\mathrm{R}$

$
R=0.2+0.3+0.4+0.5+12=13.4 \Omega
$

$
\begin{aligned}
& \mathrm{V}=9 \mathrm{~V} \\
& I=\frac{V}{R}=\frac{9}{13.4}=0.67 \mathrm{~A}
\end{aligned}
$

Hence, all resistors are in series, so 0.67 A current would flow through the $12 \Omega$ resistor.

Q.10. How many $176 \Omega$ resistors (in parallel) are required to carry 5 A on a 220 V line?

Answer:

Given: V=220V and I =5A

$
R=\frac{V}{I}=\frac{220}{5}=44 \Omega
$

Let $x$ number of resistors be connected in parallel to obtain 44 Ohm equivalent resistance.
Thus,

$
\begin{aligned}
& \frac{1}{R}=\frac{1}{176}+\frac{1}{176}+\ldots \ldots \ldots \ldots \ldots \ldots \ldots \text {............ } x \text { times } \\
& \Rightarrow \frac{1}{44}=\frac{x}{176} \\
& \Rightarrow x=\frac{176}{44}=4
\end{aligned}
$

Hence, 4 resistors of 176 Ohms are connected in parallel to obtain 44 Ohms.

Q.11. Show how you would connect three resistors, each of resistance $6 \Omega$ , so that the combination has a resistance of (i) $92 \Omega$ , (ii) $4 \Omega$ .

Answer:

(i) $R_1=R_2=R_3=6$
$\mathrm{R}=$ Equivalent resistance

$
\begin{aligned}
\frac{1}{R_{12}} & =\frac{1}{R_1}+\frac{1}{R_2} \\
& \Rightarrow \frac{1}{R_{12}}=\frac{1}{6}+\frac{1}{6} \\
& \Rightarrow \frac{1}{R_{12}}=\frac{1+1}{6} \\
& \Rightarrow R_{12}=\frac{6}{2}=3 \\
& R=R_{12}+R_3=3+6=9 \Omega
\end{aligned}
$

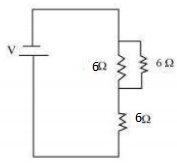
(ii)

$
R_1=R_2=R_3=6
$

$\mathrm{R}=$ Equivalent resistance

$
\begin{aligned}
& R_{12}=R_1+R_2=6+6=12 \Omega \\
& \frac{1}{R}=\frac{1}{R_{12}}+\frac{1}{R_3} \\
& \Rightarrow \frac{1}{R}=\frac{1}{12}+\frac{1}{6} \\
& \Rightarrow \frac{1}{R}=\frac{1+2}{12} \\
& \Rightarrow R=\frac{12}{3}=4
\end{aligned}
$

Q.12. Several electric bulbs designed to be used on a 220 V electric supply line, are rated 10 W. How many lamps can be connected in parallel with each other across the two wires of 220 V line if the maximum allowable current is 5 A?

Answer:

Given: $\mathrm{V}=220 \mathrm{~V}$ and $\mathrm{P}=10 \mathrm{~W}$

$
R=\frac{V^2}{P}=\frac{220^2}{10}=4840 \Omega
$

Let x be the number of bulbs.

$
\begin{aligned}
& \mathrm{I}=5 \mathrm{~A} \text { and } \mathrm{V}=220 \mathrm{~V} \\
& \qquad R=\frac{V}{I}=\frac{220}{5}=44 \Omega
\end{aligned}
$

For $x$ bulbs of resistance 4680 Ohm, are connected in parallel to obtain 44 Ohm equivalent resistance.

Thus,

$
\begin{aligned}
& \frac{1}{R}=\frac{1}{4840}+\frac{1}{4840}+\ldots \ldots \ldots \ldots \ldots \ldots . . . \text { to } x \text { times } \\
& \Rightarrow \frac{1}{44}=\frac{x}{4840} \\
& \Rightarrow x=\frac{4840}{44}=110
\end{aligned}
$

Hence, 110 bulbs of 4840 Ohms are connected in parallel to obtain 44 Ohms.

Q.13. A hot plate of an electric oven connected to a 220 V line has two resistance coils, A and B, each of $24 \Omega$ resistance, which may be used separately, in series, or in parallel. What are the currents in the three cases?

Answer:

Given : V=220V and Resistance of each coil=R =24A

When the coil is used separately, the current in the coil is

$
I=\frac{V}{R}=\frac{220}{24}=9.16 A
$

When two coils are connected in series, the net resistance is

$
R=R_1+R_2=24+24=48 \Omega
$

current in coil is I'

$
I^{\prime}=\frac{V}{R}=\frac{220}{48}=4.58 \mathrm{~A}
$

When two coils are connected in parallel, the net resistance is

$
\begin{aligned}
& \frac{1}{R}=\frac{1}{24}+\frac{1}{24}=\frac{2}{24} \\
& \Rightarrow R=12 \Omega
\end{aligned}
$

current in the coil is I"

$
I^{\prime \prime}=\frac{V}{R}=\frac{220}{12}=18.33 \mathrm{~A}
$

Q.14. Compare the power used in the $2 \Omega$ resistor in each of the following circuits:

(i) a 6 V battery in series with $1 \Omega$ and $2 \Omega$ resistors

(ii) a 4 V battery in parallel with $12 \Omega$ and $2 \Omega$ resistors.

Answer:

i) Given: V=6V

$\mathrm{R}=1+2=30 \mathrm{hm}$

$
I=\frac{V}{R}=\frac{6}{3}=2 A
$

In a series current is constant.
So, power $=P$

$
P=I^2 R=2^2 \times 2=8 W
$

ii) Given: $V=6 \mathrm{~V}, \mathrm{R}=2 \mathrm{Ohm}$

In, parallel combination voltage in the circuit is constant.
So, power $=P$

$
P=\frac{V^2}{R}=\frac{4^2}{2}=8 W
$

Q.15. Two lamps, one rated 100 W at 220 V, and the other 60 W at 220 V, are connected in parallel to an electric mains supply. What current is drawn from the line if the supply voltage is 220 V?

Answer:

Given :

For lamp one: Power $=\mathrm{P_1} =100 \mathrm{~W}$ and $\mathrm{V}=220 \mathrm{~V}$

$
I_1=\frac{P_1}{V}=\frac{100}{220}=0.455 \mathrm{~A}
$

For lamp two: Power $=\mathrm{P_2} =60 \mathrm{~W}$ and $\mathrm{V}=220 \mathrm{~V}$

$
I_2=\frac{P_2}{V}=\frac{60}{220}=0.273 \mathrm{~A}
$

Thus, the net current drawn from the supply is $0.455+0.273=0.728 \mathrm{~A}$

Q.16. Which uses more energy, a 250 W TV set in 1 hr, or a 1200 W toaster in 10 minutes?

Answer:

For the TV set :

Given : Power $=250 \mathrm{~W}$ and time $=1 \mathrm{hr}=3600$ seconds
Energy consumed $=\mathrm{H}=\mathrm{PI}$

$
H=250 \times 3600=900000 J
$

For toaster :
Given : Power $=1200 \mathrm{~W}$ and time $=10$ minutes $=600$ seconds
Energy consumed $=\mathrm{H}=\mathrm{PI}$

$
H=1200 \times 600=720000 J
$

Thus, the TV set uses more energy than a toaster.

Q.17. An electric heater of resistance $8 \Omega$ draws 15 A from the service mains 2 hours. Calculate the rate at which heat is developed in the heater.

Answer:

Given: R=8 Ohm ,I=15A and t= 2hr

The heat developed in the heater is H.

The heat developed in the heater is H.

$
H=I^2 R t
$

The rate at which heat is developed is given as

$
\frac{I^2 R t}{t}=I^2 R=15^2 \times 8=1800 \mathrm{~J} / \mathrm{s}
$

Q.18(a). Explain the following: Why is tungsten used almost exclusively for the filament of electric lamps?

Answer:

Tungsten is used almost exclusively for the filament of electric lamps because the melting point of tungsten is very high. The bulb glows at a very high temperature. So tungsten filament does not melt when the bulb glows.

Q.18.(b) Explain the following: Why are the conductors of electric heating devices, such as bread-toasters and electric irons, made of an alloy rather than a pure metal?

Answer:

The conductors of electric heating devices, such as bread toasters and electric irons, are made of an alloy rather than a pure metal because the resistivity of the alloy is greater than a pure metal. So the resistance will be high and the heating effect will be high.

Q.18.(c) Explain the following: Why is the series arrangement not used for domestic circuits?

Answer:

If any of the elements in the circuit get damaged, the entire circuit will be affected. If an element breaks, there will not be any current flow through the circuit. So the series circuit is not preferred in the domestic circuit.

Q.18.(d) Explain the following: How does the resistance of a wire vary with its area of cross-section?

Answer:

We know that

$\begin{aligned} & R=\frac{\rho l}{A} \\ & R \alpha \frac{1}{A}\end{aligned}$

Thus, the resistance of a wire is inversely proportional to its area of cross-section.

Q.18.(e) Explain the following: Why are copper and aluminium wires usually employed for electricity transmission?

Answer:

Copper and aluminium wires are usually employed for electricity transmission because they have low resistivity and are good conductors of electricity.