• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
NCERT Solutions for Exercise 6.3 Class 10 Maths Chapter 6 - Triangles

NCERT Solutions for Exercise 6.3 Class 10 Maths Chapter 6 - Triangles

Edited By Ramraj Saini | Updated on Nov 21, 2023 01:31 PM IST | #CBSE Class 10th
Upcoming Event
CBSE Class 10th  Exam Date : 15 Feb' 2025 - 15 Feb' 2025

NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.3

NCERT Solutions for Exercise 6.3 Class 10 Maths Chapter 6 Triangles are discussed here. These NCERT solutions are created by subject matter expert at Careers360 considering the latest syllabus and pattern of CBSE 2023-24. Class 10 maths ex 6.3 contains critical criteria or theorems for congruence such as Angle-Angle-Angle (AAA), Angle-Side-Angle (ASA), and Side-Side-Side (SSS). It contains 16 questions that cover all parts of the previously given theorems.

This Story also Contains
  1. NCERT Solutions For Class 10 Maths Chapter 6 Exercise 6.3
  2. Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 6 exercise 6.3
  3. Assess NCERT Solutions for Class 10 Maths chapter 6 exercise 6.3
  4. More About NCERT Solutions for Class 10 Maths Exercise 6.3
  5. Benefits of NCERT Solutions for Class 10 Maths Exercise 6.3
  6. NCERT Solutions of Class 10 Subject Wise
  7. Subject Wise NCERT Exemplar Solutions
NCERT Solutions for Exercise 6.3 Class 10 Maths Chapter 6 - Triangles
NCERT Solutions for Exercise 6.3 Class 10 Maths Chapter 6 - Triangles

NCERT solutions for exercise 6.3 Class 10 Maths chapter 6 Triangles discusses the standards required to demonstrate the resemblance of triangles. 10th class Maths exercise 6.3 answers are designed as per the students demand covering comprehensive, step by step solutions of every problem. Practice these questions and answers to command the concepts, boost confidence and in depth understanding of concepts. Students can find all exercise together using the link provided below.

Pearson | PTE

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

Apply

Download Free Pdf of NCERT Solutions for Class 10 Maths chapter 6 exercise 6.3

Download PDF

Assess NCERT Solutions for Class 10 Maths chapter 6 exercise 6.3

Triangles Class 10 Chapter 6 Exercise: 6.3

Q1 State which pairs of triangles in Fig. 6.34 are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

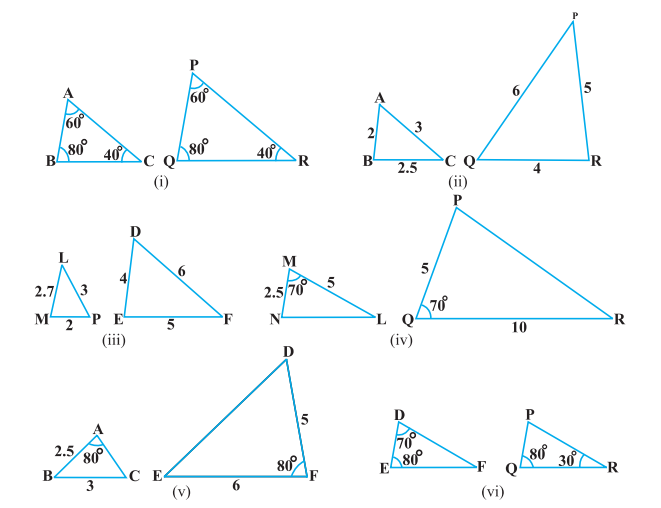
1635924024150

Answer:

(i) \angle A=\angle P=60 \degree

\angle B=\angle Q=80 \degree

\angle C=\angle R=40 \degree

\therefore \triangle ABC \sim \triangle PQR (By AAA)

So , \frac{AB}{QR}=\frac{BC}{RP}=\frac{CA}{PQ}


(ii) As corresponding sides of both triangles are proportional.

\therefore \triangle ABC \sim \triangle PQR (By SSS)


(iii) Given triangles are not similar because corresponding sides are not proportional.


(iv) \triangle MNL \sim \triangle PQR by SAS similarity criteria.


(v) Given triangles are not similar because the corresponding angle is not contained by two corresponding sides


(vi) In \triangle DEF , we know that

\angle D+\angle E+\angle F=180 \degree

\Rightarrow 70 \degree+80 \degree+\angle F=180 \degree

\Rightarrow 150 \degree+\angle F=180 \degree

\Rightarrow \angle F=180 \degree-150 \degree=30 \degree


In \triangle PQR , we know that

\angle P+\angle Q+\angle R=180 \degree

\Rightarrow 30 \degree+80 \degree+\angle R=180 \degree

\Rightarrow 110 \degree+\angle R=180 \degree

\Rightarrow \angle R=180 \degree-110 \degree=70 \degree

\angle Q=\angle P=70 \degree

\angle E=\angle Q=80 \degree

\angle F=\angle R=30 \degree

\therefore \triangle DEF\sim \triangle PQR ( By AAA)

Q2 In Fig. 6.35, \Delta ODC \sim \Delta OBA , \angle BOC = 125 \degree and \angle CDO = 70 \degree . Find \angle DOC , \angle DCO , \angle OAB

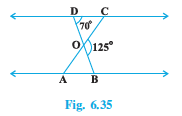
1635924052755

Answer:

Given : \Delta ODC \sim \Delta OBA , \angle BOC = 125 \degree and \angle CDO = 70 \degree

\angle DOC+\angle BOC=180 \degree (DOB is a straight line)

\Rightarrow \angle DOC+125 \degree=180 \degree

\Rightarrow \angle DOC=180 \degree-125 \degree

\Rightarrow \angle DOC=55 \degree

In \Delta ODC ,

\angle DOC+\angle ODC+\angle DCO=180 \degree

\Rightarrow 55 \degree+ 70 \degree+\angle DCO=180 \degree

\Rightarrow \angle DCO+125 \degree=180 \degree

\Rightarrow \angle DCO=180 \degree-125 \degree

\Rightarrow \angle DCO=55 \degree

Since , \Delta ODC \sim \Delta OBA , so

\Rightarrow\angle OAB= \angle DCO=55 \degree ( Corresponding angles are equal in similar triangles).

Q3 Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that \frac{OA }{OC} = \frac{OB }{OD }

Answer:

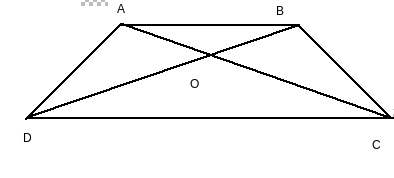
1635924090157

In \triangle DOC\, and\, \triangle BOA , we have

\angle CDO=\angle ABO ( Alternate interior angles as AB||CD )

\angle DCO=\angle BAO ( Alternate interior angles as AB||CD )

\angle DOC=\angle BOA ( Vertically opposite angles are equal)

\therefore \triangle DOC\, \sim \, \triangle BOA ( By AAA)

\therefore \frac{DO}{BO}=\frac{OC}{OA} ( corresponding sides are equal)

\Rightarrow \frac{OA }{OC} = \frac{OB }{OD }

Hence proved.

Q4 In Fig. 6.36, \frac{QR }{QS } = \frac{QT}{PR} and \angle 1 = \angle 2 . Show that \Delta PQS \sim \Delta TQR

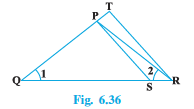
1635924132584


Answer:

Given : \frac{QR }{QS } = \frac{QT}{PR} and \angle 1 = \angle 2

To prove : \Delta PQS \sim \Delta TQR

In \triangle PQR , \angle PQR=\angle PRQ

\therefore PQ=PR

\frac{QR }{QS } = \frac{QT}{PR} (Given)

\Rightarrow \frac{QR }{QS } = \frac{QT}{PQ}


In \Delta PQS\, and\, \Delta TQR ,

\Rightarrow \frac{QR }{QS } = \frac{QT}{PQ}

\angle Q=\angle Q (Common)

\Delta PQS \sim \Delta TQR ( By SAS)

Q5 S and T are points on sides PR and QR of \Delta PQR such that \angle P = \angle RTS. Show that \Delta RPQ ~ \Delta RTS.

Answer:

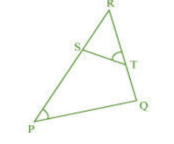
1635924147463

Given : \angle P = \angle RTS

To prove RPQ ~ \Delta RTS.

In \Delta RPQ and \Delta RTS,

\angle P = \angle RTS (Given )

\angle R = \angle R (common)

\Delta RPQ ~ \Delta RTS. ( By AA)

Q6 In Fig. 6.37, if \Delta ABE \equiv \Delta ACD, show that \Delta ADE ~ \Delta ABC.

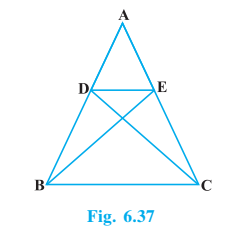
1635924156441

Answer:

Given : \triangle ABE \cong \triangle ACD

To prove ADE ~ \Delta ABC.

Since \triangle ABE \cong \triangle ACD

AB=AC ( By CPCT)

AD=AE (By CPCT)

In \Delta ADE and \Delta ABC,

\angle A=\angle A ( Common)

and

\frac{AD}{AB}=\frac{AE}{AC} ( AB=AC and AD=AE )

Therefore, \Delta ADE ~ \Delta ABC. ( By SAS criteria)

Q7 (1) In Fig. 6.38, altitudes AD and CE of \Delta ABC intersect each other at the point P. Show that: \Delta AEP \sim \Delta CDP

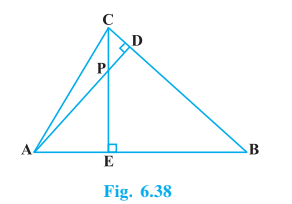
1635924178546

Answer:

To prove : \Delta AEP \sim \Delta CDP

In \Delta AEP \, \, and\, \, \Delta CDP ,

\angle AEP=\angle CDP ( Both angles are right angle)

\angle APE=\angle CPD (Vertically opposite angles )

\Delta AEP \sim \Delta CDP ( By AA criterion)

Q7 (2) In Fig. 6.38, altitudes AD and CE of \Delta ABC intersect each other at the point P. Show that: \Delta ABD \sim \Delta CBE

Answer:

To prove : \Delta ABD \sim \Delta CBE

In \Delta ABD \, \, and\, \, \Delta CBE ,

\angle ADB=\angle CEB ( Both angles are right angle)

\angle ABD=\angle CBE (Common )

\Delta ABD \sim \Delta CBE ( By AA criterion)

Q7 (3) In Fig. 6.38, altitudes AD and CE of \Delta ABC intersect each other at the point P. Show that: \Delta AEP \sim \Delta ADB

Answer:

To prove : \Delta AEP \sim \Delta ADB

In \Delta AEP \, \, \, and\, \, \Delta ADB ,

\angle AEP=\angle ADB ( Both angles are right angle)

\angle A=\angle A (Common )

\Delta AEP \sim \Delta ADB ( By AA criterion)

Q7 (4) In Fig. 6.38, altitudes AD and CE of \Delta ABC intersect each other at the point P. Show that: \Delta PDC \sim \Delta BEC

Answer:

To prove : \Delta PDC \sim \Delta BEC

In \Delta PDC \, \, and\, \, \, \Delta BEC ,

\angle CDP=\angle CEB ( Both angles are right angle)

\angle C=\angle C (Common )

\Delta PDC \sim \Delta BEC ( By AA criterion)

Q8 E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that \Delta ABE \sim \Delta CFB

Answer:

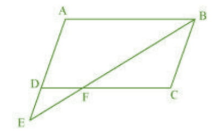
1635924231460

To prove : \Delta ABE \sim \Delta CFB

In \Delta ABE \, \, \, and\, \, \Delta CFB ,

\angle A=\angle C ( Opposite angles of a parallelogram are equal)

\angle AEB=\angle CBF ( Alternate angles of AE||BC)

\Delta ABE \sim \Delta CFB ( By AA criterion )

Q9 In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that \frac{CA }{PA } = \frac{BC }{MP}

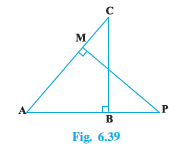
Answer:

To prove :

\frac{CA }{PA } = \frac{BC }{MP}

In \Delta ABC \, \, and\, \, \Delta AMP ,

\angle ABC=\angle AMP ( Each 90 \degree )

\angle A=\angle A ( common)

\Delta ABC \sim \Delta AMP ( By AA criterion )

\frac{CA }{PA } = \frac{BC }{MP} ( corresponding parts of similar triangles )

Hence proved.

Q10 (1) CD and GH are respectively the bisectors of \angle ACB and \angle EGF such that D and H lie on sides AB and FE of \Delta ABC\: \: and\: \: \Delta EGF respectively. If \Delta ABC \sim \Delta EGF , show that: \frac{CD}{GH} = \frac{AC}{FG}

Answer:

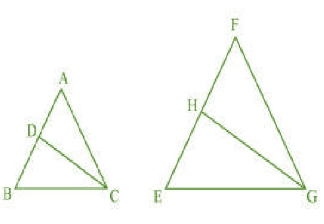
1635924284479

To prove :

\frac{CD}{GH} = \frac{AC}{FG}

Given : \Delta ABC \sim \Delta EGF

\angle A=\angle F,\angle B=\angle E\, \, and \, \, \angle ACB=\angle FGE,\angle ACB=\angle FGE

\therefore \angle ACD=\angle FGH ( CD and GH are bisectors of equal angles)

\therefore \angle DCB=\angle HGE ( CD and GH are bisectors of equal angles)

In \Delta ACD \, \, and\, \, \Delta FGH

\therefore \angle ACD=\angle FGH ( proved above)

\angle A=\angle F ( proved above)

\Delta ACD \sim \Delta FGH ( By AA criterion)

\Rightarrow \frac{CD}{GH} = \frac{AC}{FG}

Hence proved.

Q 10 (2) CD and GH are respectively the bisectors of \angle ABC \: \:and \: \: \angle EGF such that D and H lie on sides AB and FE of \Delta ABC \: \:and \: \: \Delta EGF respectively. If \Delta ABC \sim \Delta EGF , show that: \Delta DCB \sim \Delta HGE

Answer:

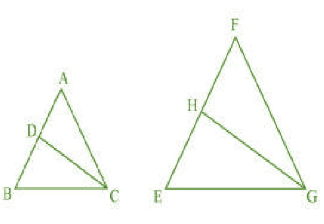
1635924301949

To prove : \Delta DCB \sim \Delta HGE

Given : \Delta ABC \sim \Delta EGF

In \Delta DCB \,\, \, and\, \, \Delta HGE ,

\therefore \angle DCB=\angle HGE ( CD and GH are bisectors of equal angles)

\angle B=\angle E ( \Delta ABC \sim \Delta EGF )

\Delta DCB \sim \Delta HGE ( By AA criterion )

Q10 (3) CD and GH are respectively the bisectors of \angle ABC \: \:and \: \: \angle EGF such that D and H lie on sides AB and FE of \Delta ABC \: \:and \: \: \Delta EGF respectively. If \Delta ABC\sim \Delta EGF , show that: \Delta DCA \sim \Delta HGF

Answer:

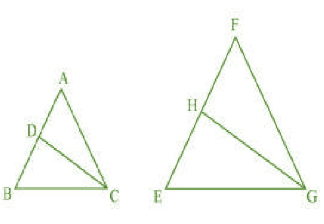
1635924370515

To prove : \Delta DCA \sim \Delta HGF

Given : \Delta ABC \sim \Delta EGF

In \Delta DCA \, \, \, and\, \, \Delta HGF ,

\therefore \angle ACD=\angle FGH ( CD and GH are bisectors of equal angles)

\angle A=\angle F ( \Delta ABC \sim \Delta EGF )

\Delta DCA \sim \Delta HGF ( By AA criterion )

Q11 In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD \perp BC and EF \perp AC , prove that \Delta ABD \sim \Delta ECF

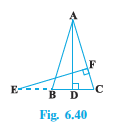
1635924369822

Answer:

To prove : \Delta ABD \sim \Delta ECF

Given: ABC is an isosceles triangle.

AB=AC \, \, and\, \, \angle B=\angle C

In \Delta ABD \, \, and\, \, \Delta ECF ,

\angle ABD=\angle ECF ( \angle ABD=\angle B=\angle C=\angle ECF )

\angle ADB=\angle EFC ( Each 90 \degree )

\Delta ABD \sim \Delta ECF ( By AA criterion)

Q12 Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of \Delta PQR (see Fig. 6.41). Show that \Delta ABC \sim \Delta PQR

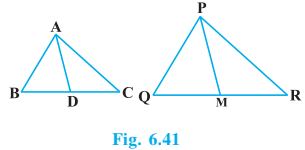
1635924392444

Answer:

AD and PM are medians of triangles. So,

BD=\frac{BC}{2}\, and\, QM=\frac{QR}{2}

Given :

\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AD}{PM}

\Rightarrow \frac{AB}{PQ}=\frac{\frac{1}{2}BC}{\frac{1}{2}QR}=\frac{AD}{PM}

\Rightarrow \frac{AB}{PQ}=\frac{BD}{QM}=\frac{AD}{PM}

In \triangle ABD\, and\, \triangle PQM,

\frac{AB}{PQ}=\frac{BD}{QM}=\frac{AD}{PM}

\therefore \triangle ABD\sim \triangle PQM, (SSS similarity)

\Rightarrow \angle ABD=\angle PQM ( Corresponding angles of similar triangles )

In \triangle ABC\, and\, \triangle PQR,

\Rightarrow \angle ABD=\angle PQM (proved above)

\frac{AB}{PQ}=\frac{BC}{QR}

Therefore, \Delta ABC \sim \Delta PQR . ( SAS similarity)

Q13 D is a point on the side BC of a triangle ABC such that \angle ADC = \angle BAC . Show that CA^2 = CB.CD.

Answer:

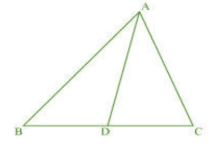
1635924451786

In, \triangle ADC \, \, and\, \, \triangle BAC,

\angle ADC = \angle BAC ( given )

\angle ACD = \angle BCA (common )

\triangle ADC \, \, \sim \, \, \triangle BAC, ( By AA rule)

\frac{CA}{CB}=\frac{CD}{CA} ( corresponding sides of similar triangles )

\Rightarrow CA^2=CB\times CD

Q14 Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that \Delta ABC \sim \Delta PQR

Answer:

1635924470215

\frac{AB}{PQ}=\frac{AC}{PR}=\frac{AD}{PM} (given)

Produce AD and PM to E and L such that AD=DE and PM=DE. Now,

join B to E,C to E,Q to L and R to L.

AD and PM are medians of a triangle, therefore

QM=MR and BD=DC

AD = DE (By construction)

PM=ML (By construction)

So, diagonals of ABEC bisecting each other at D,so ABEC is a parallelogram.

Similarly, PQLR is also a parallelogram.

Therefore, AC=BE ,AB=EC and PR=QL,PQ=LR

\frac{AB}{PQ}=\frac{AC}{PR}=\frac{AD}{PM} (Given )

\Rightarrow \frac{AB}{PQ}=\frac{BE}{QL}=\frac{2.AD}{2.PM}

\Rightarrow \frac{AB}{PQ}=\frac{BE}{QL}=\frac{AE}{PL}

\Delta ABE \sim \Delta PQL (SSS similarity)

\angle BAE=\angle QPL ...................1 (Corresponding angles of similar triangles)

Similarity, \triangle AEC=\triangle PLR

\angle CAE=\angle RPL ........................2

Adding equation 1 and 2,

\angle BAE+\angle CAE=\angle QPL+\angle RPL

\angle CAB=\angle RPQ ............................3

In \triangle ABC\, and\, \, \triangle PQR,

\frac{AB}{PQ}=\frac{AC}{PR} ( Given )

\angle CAB=\angle RPQ ( From above equation 3)

\triangle ABC\sim \triangle PQR ( SAS similarity)

Q15 A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

Answer:

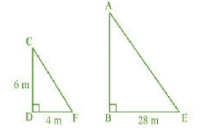
1635924490568

CD = pole

AB = tower

Shadow of pole = DF

Shadow of tower = BE

In \triangle ABE\, \, and\, \triangle CDF,

\angle CDF=\angle ABE ( Each 90 \degree )

\angle DCF=\angle BAE (Angle of sun at same place )

\triangle ABE\, \, \sim \, \triangle CDF, (AA similarity)

\frac{AB}{CD}=\frac{BE}{QL}

\Rightarrow \frac{AB}{6}=\frac{28}{4}

\Rightarrow AB=42 cm

Hence, the height of the tower is 42 cm.

Q16 If AD and PM are medians of triangles ABC and PQR, respectively where \Delta AB C \sim \Delta PQR , prove that \frac{AB}{PQ} = \frac{AD }{PM}

Answer:

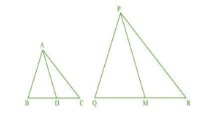
1635924504095

\Delta AB C \sim \Delta PQR ( Given )

\frac{AB}{PQ}=\frac{AC}{PR}=\frac{BC}{QR} ............... ....1( corresponding sides of similar triangles )

\angle A=\angle P,\angle B=\angle Q,\angle C=\angle R ....................................2

AD and PM are medians of triangle.So,

BD=\frac{BC}{2}\, and\, QM=\frac{QR}{2} ..........................................3

From equation 1 and 3, we have

\frac{AB}{PQ}=\frac{BD}{QM} ...................................................................4

In \triangle ABD\, and\, \triangle PQM,

\angle B=\angle Q (From equation 2)

\frac{AB}{PQ}=\frac{BD}{QM} (From equation 4)

\triangle ABD\, \sim \, \triangle PQM, (SAS similarity)

\frac{AB}{PQ}=\frac{BD}{QM}=\frac{AD}{PM}


More About NCERT Solutions for Class 10 Maths Exercise 6.3

NCERT solutions Class 10 Maths chapter 6 exercise 6.3 Triangles contains well-written examples that demonstrate the key similarity theorems. Certain implications can be taken from the presented theories, such as the AA property, which states that if two angles of one triangle are equal to two angles of another triangle, then the two triangles are comparable (similar to each other) as the corresponding third angle of the triangle also becomes equal as the sum of the total angles of a triangle remains fixed to 180 degrees. Before moving on to the exercise questions, students must ensure that they have thoroughly practiced these examples. Furthermore, the chapter's highlights can be refreshed on a regular basis to keep the concepts fresh. Students can also access Triangles Class 10 Notes here and use them for quickly revision of the concepts related to Triangles.

Benefits of NCERT Solutions for Class 10 Maths Exercise 6.3

  • If you go through the NCERT solution for Class 10 Maths chapter 6 exercise 6.3, we can easily revise the concepts of exercise 6.1 and 6.2 which deals with the measurement aspects of the sides of the triangle.
  • Exercise 6.3 Class 10 Maths, is based on conditions for the concurrency of triangles.
  • NCERT solutions for Class 10 Maths chapter 6 exercise 6.3 revolves around the different forms of similarity aspect of triangles.

Also, See:

NCERT Solutions of Class 10 Subject Wise

Subject Wise NCERT Exemplar Solutions

Frequently Asked Questions (FAQs)

1. What is the core concept of Class 10 Maths chapter 6 exercise 6.3 ?

This exercise is about the criteria or theorems for congruence of triangles. Practice this class 10 ex 6.3 to command the concepts.


2. Name all the criteria for similarity of triangles according to NCERT solutions Class 10 Maths chapter 6 exercise 6.?

In this class 10 maths ex 6.3 following theorems are discussed in detail.

  1. Angle-angle-angle

  2. Angle-side-angle

  3. Side-side-side

  4. Angle-angle

  5. Angle-angle-side

  6. Side-angle-side

Go through this ex 6.3 class 10 to get deeper understanding of related concepts.

3. What is the total of a triangle's angels?

The sum of a triangle's angels is 180 degrees.


4. Is similarity a sign of congruence between the figures?

No, similarity simply refers to the shape of the figures; it does not imply equality.


5. If two corresponding angels of two triangles are same does this mean the triangles are similar?

Yes, because a triangle has three angles and their sum remains 180 degrees. So, if two angels are equal then the third also becomes equal. 


6. If all the three sides of two triangles are in proportion, then does this means the triangles are similar?

Yes, if all the three sides of two triangles are in proportion, then does this means the triangles are similar. By side-side-side criteria.


7. What will happen if the ratio of the sides of two similar triangles becomes equal to 1?

If the ratio becomes equal to 1 then the triangles are congruent to each other.


8. For similar triangles, what is the purpose of side ratios?

We can find the length of the corresponding side of the other triangle using the side ratio and the length of any side. Practice 10th class maths exercise 6.3 answers to command the concepts.

Also Read

Articles

Upcoming School Exams

National Institute of Open Schooling 10th examination

Application Date:21 November,2024 - 20 December,2024

National Institute of Open Schooling 12th Examination

Application Date:21 November,2024 - 20 December,2024

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Himachal Pradesh Board of Secondary Education 10th Examination

Application Date:02 December,2024 - 16 December,2024

Himachal Pradesh Board of Secondary Education 12th Examination

Application Date:02 December,2024 - 16 December,2024

View All School Exams

Certifications By Top Providers

My SQL Basics
 Via Great Learning
Full-Stack Web Development
 Via Masai School
Digital Banking Business Model
 Via State Bank of India
Business Analytics Foundations
 Via PW Skills
Full-Stack Android Development
 Via Masai School
Data Science for Beginners
 Via Board Infinity
Edx
 1115 courses
Coursera
 816 courses
Udemy
 394 courses
Futurelearn
 295 courses
Harvard University, Cambridge
 98 courses
University of Michigan, Ann Arbor
 83 courses

Explore Top Universities Across Globe

University of Essex, Colchester
  Wivenhoe Park Colchester CO4 3SQ
University College London, London
  Gower Street, London, WC1E 6BT
The University of Edinburgh, Edinburgh
  Old College, South Bridge, Edinburgh, Post Code EH8 9YL
University of Bristol, Bristol
  Beacon House, Queens Road, Bristol, BS8 1QU
University of Delaware, Newark
  Newark, DE 19716
University of Nottingham, Nottingham
  University Park, Nottingham NG7 2RD

Related E-books & Sample Papers

Questions related to CBSE Class 10th

Have a question related to CBSE Class 10th ?
sadhu ashram ramgart road aligarh

If you're looking for directions or steps to reach Sadhu Ashram on Ramgart Road in Aligarh, here’s how you can get there:

Steps to Reach Sadhu Ashram, Ramgart Road, Aligarh:

  1. Starting Point:

    • Determine your starting point in Aligarh or the nearby area.

  2. Use Google Maps:

    • Open Google Maps on your phone or computer.
    • Enter "Sadhu Ashram, Ramgart Road, Aligarh" as your destination.
    • Follow the navigation instructions provided by Google Maps.

  3. By Local Transport:

    • Auto-rickshaw/Taxi: Hire an auto-rickshaw or taxi and inform the driver about your destination. Most local drivers should be familiar with Sadhu Ashram.
    • Bus: Check if there are any local buses that operate on Ramgart Road. Ask the bus conductor if the bus stops near Sadhu Ashram.

  4. Landmarks to Look For:

    • As you approach Ramgart Road, look for local landmarks that might help you confirm you’re on the right path, such as known shops, temples, or schools nearby.

  5. Ask for Directions:

    • If you're unsure, ask locals for directions to Sadhu Ashram on Ramgart Road. It's a known location in the area.

  6. Final Destination:

    • Once you reach Ramgart Road, Sadhu Ashram should be easy to spot. Look for any signage or ask nearby people to guide you to the exact location.

If you need detailed directions from a specific location or more information about Sadhu Ashram, feel free to ask

Read Complete Answer
sai raja 01 September,2024
show the previous year exams ?

Hello Aspirant,  Hope your doing great,  your question was incomplete and regarding  what exam your asking.

Read Complete Answer
SWETCHCHA MISKA 10 July,2024
as an icse student in class 10 is above 80 percent good enough to get into commerce in 11th cbse

Yes, scoring above 80% in ICSE Class 10 exams typically meets the requirements to get into the Commerce stream in Class 11th under the CBSE board . Admission criteria can vary between schools, so it is advisable to check the specific requirements of the intended CBSE school. Generally, a good academic record with a score above 80% in ICSE 10th result is considered strong for such transitions.

Read Complete Answer
Manasvini Gupta 23 July,2024
i had cleared 10th from cbse in 2022 2 years ago now i wish to apply for 12th as private candidate in 2025. can i do so?

hello Zaid,

Yes, you can apply for 12th grade as a private candidate .You will need to follow the registration process and fulfill the eligibility criteria set by CBSE for private candidates.If you haven't given the 11th grade exam ,you would be able to appear for the 12th exam directly without having passed 11th grade. you will need to give certain tests in the school you are getting addmission to prove your eligibilty.

best of luck!

Read Complete Answer
Ashvadha 03 July,2024
i had cleared 10th in 2022 from cbse can i apply for 12th as private candidate this year?

According to cbse norms candidates who have completed class 10th, class 11th, have a gap year or have failed class 12th can appear for admission in 12th class.for admission in cbse board you need to clear your 11th class first and you must have studied from CBSE board or any other recognized and equivalent board/school.

You are not eligible for cbse board but you can still do 12th from nios which allow candidates to take admission in 12th class as a private student without completing 11th.

Read Complete Answer
sadafreen356 03 July,2024
View All

Popular CBSE Class 10th Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
November 20, 2024 - 11:18 PM IST :
Board Exam Date 2025 Live: Bihar Class 10, 12 model papers out, time table soon; updates on CBSE, UP
December 06, 2024 - 10:42 PM IST
CBSE Class 10 board exams from February 15 to March 18; download date sheet 2025 PDF
November 20, 2024 - 10:02 PM IST
CBSE Date Sheet 2025 Live: CBSE Class 10, 12 board exam timetable soon at cbse.gov.in; practical dates
November 14, 2024 - 03:21 PM IST
CBSE Date Sheet 2025 Live: CBSE to announce Class 10, 12 board exam dates soon at cbse.gov.in; sample paper
November 13, 2024 - 07:53 AM IST
CBSE Board Exam 2025: Class 10, 12 practical exam dates out at cbse.gov.in; passing marks
October 24, 2024 - 09:54 PM IST
CBSE urges schools to complete 100% registration of Class 9, 11 students by October 16; late fee for delays
October 11, 2024 - 08:56 AM IST
CBSE sample papers 2024-25 for Class 10, 12 out at cbseacademic.nic.in; marking scheme
September 05, 2024 - 07:38 PM IST

Stay up-to date with CBSE Class 10th News

Back to top