NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.2 - Triangles

Q2 (1) E and F are points on the sides PQ and PR respectively of a $\triangle$ PQR. For each of the following cases, state whether EF || QR: PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

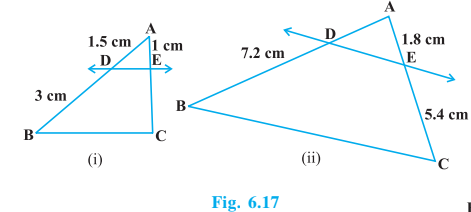
Answer:

(i)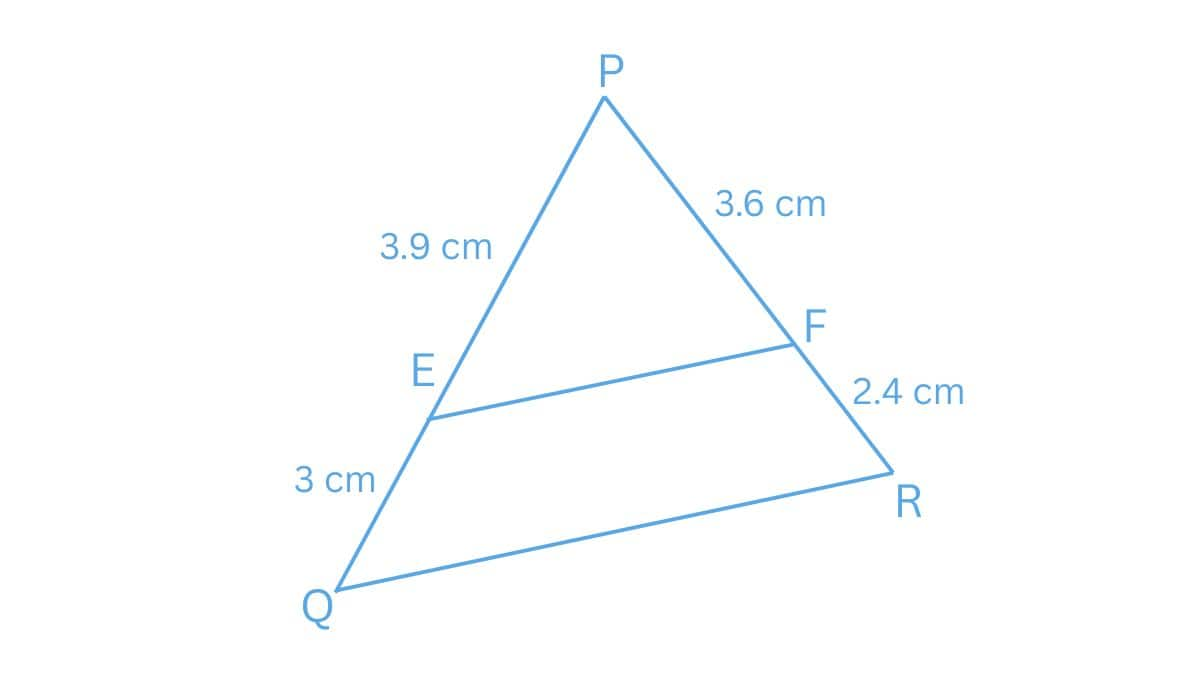

Given :

PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

$\frac{PE}{EQ}=\frac{3.9}{3}=1.3\, cm$ and $\frac{PF}{FR}=\frac{3.6}{2.4}=1.5\, cm$

We have

$\frac{PE}{EQ} \neq \frac{PF}{FR}$

Hence, EF is not parallel to QR.

Q2 (2) E and F are points on the sides PQ and PR respectively of a triangle PQR. For each of the following cases, state whether EF || QR : PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

Answer:

(ii)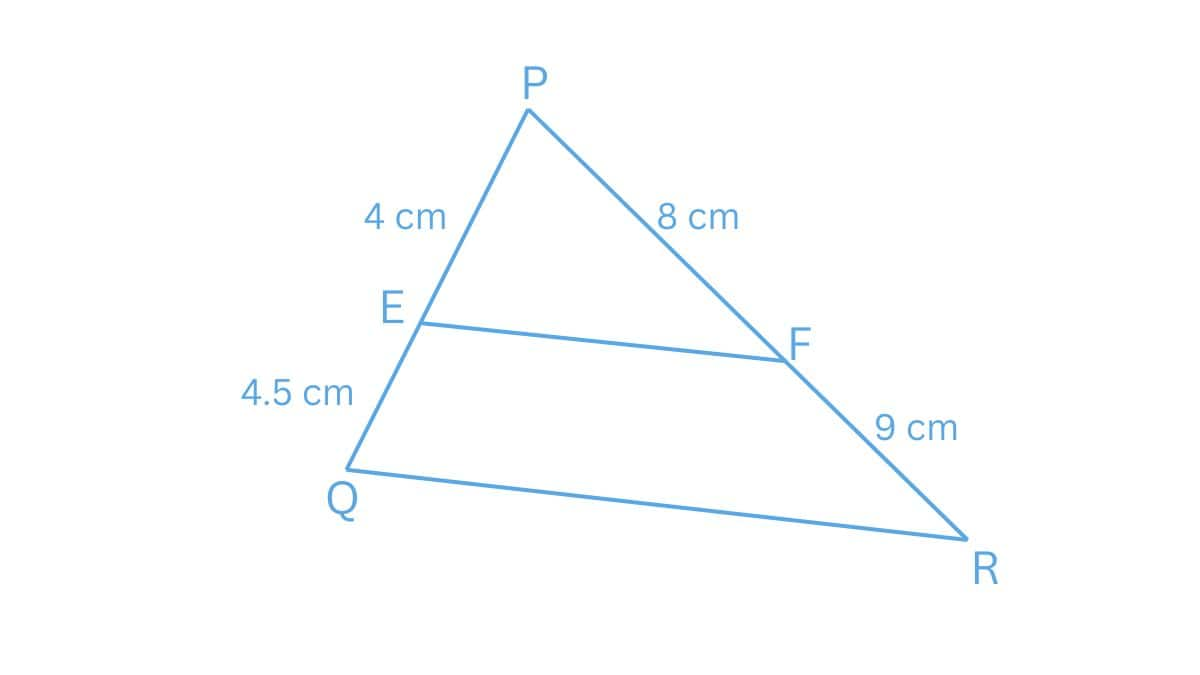

Given :

PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

$\frac{PE}{EQ}=\frac{4}{4.5}=\frac{8}{9}\, cm$ and $\frac{PF}{FR}=\frac{8}{9}\, cm$

We have

$\frac{PE}{EQ} = \frac{PF}{FR}$

Hence, EF is parallel to QR.

Q2 (3) E and F are points on the sides PQ and PR respectively of a triangle PQR. For each of the following cases, state whether EF || QR : PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

Answer:

(iii)

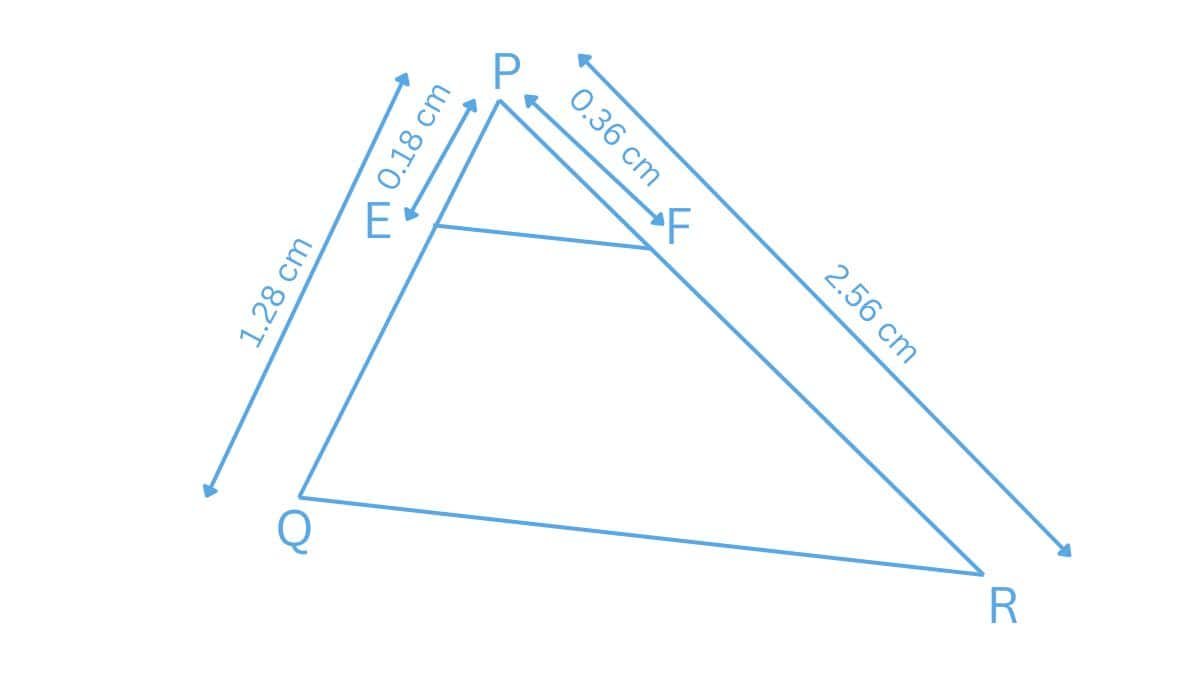
Given:

PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

$\frac{PE}{PQ}=\frac{0.18}{1.28}=\frac{9}{64}\, cm$ and $\frac{PF}{PR}=\frac{0.36}{2.56}=\frac{9}{64}\, cm$

We have

$\frac{PE}{EQ} = \frac{PF}{FR}$

Hence, EF is parallel to QR.

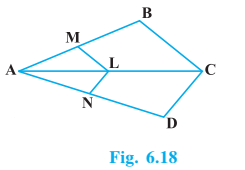
Q3 In Fig. 6.18, if LM || CB and LN || CD, prove that $\frac{AM}{AB} = \frac{AN}{AD }$

Answer:

Given : LM || CB and LN || CD

To prove :

$\frac{AM}{AB} = \frac{AN}{AD }$

Since , LM || CB so we have

$\frac{AM}{AB}=\frac{AL}{AC}............(1)$

Also, LN || CD

$\frac{AL}{AC}=\frac{AN}{AD}..............(2)$

From equations 1 and 2, we have

$\frac{AM}{AB} = \frac{AN}{AD }$

Hence proved.

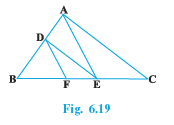
Q4 In Fig. 6.19, DE || AC and DF || AE. Prove that BF / FE = BE / EC

Answer:

Given: DE || AC and DF || AE.

To prove:

$\frac{BF}{FE} = \frac{BE}{EC }$

Since , DE || AC so we have

$\frac{BD}{DA}=\frac{BE}{EC}...........(1)$

Also, DF || AE

$\frac{BD}{DA}=\frac{BF}{FE}.............(2)$

From equations (1) and (2), we have

$\frac{BF}{FE} = \frac{BE}{EC }$

Hence proved.

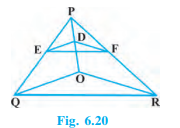
Q5 In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.

Answer:

Given: DE || OQ and DF || OR.

To prove EF || QR.

Since DE || OQ, we have

$\frac{PE}{EQ}=\frac{PD}{DO}..........(1)$

Also, DF || OR

$\frac{PF}{FR}=\frac{PD}{DO}.............(2)$

From equations (1) and (2), we have

$\frac{PE}{EQ} = \frac{PF}{FR }$

Thus, EF || QR. (Converse of the basic proportionality theorem)

Hence proved.

Q6 In Fig. 6.21, A, B, and C are points on OP, OQ and OR, respectively, such that AB || PQ and AC || PR. Show that BC || QR.

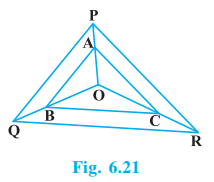
Answer:

Given: AB || PQ and AC || PR

To prove: BC || QR

Since, AB || PQ so we have

$\frac{OA}{AP}=\frac{OB}{BQ}............(1)$

Also, AC || PR

$\frac{OA}{AP}=\frac{OC}{CR}..............(2)$

From equations (1) and (2), we have

$\frac{OB}{BQ} = \frac{OC}{CR }$

Therefore, BC || QR. (converse basic proportionality theorem)

Hence proved.

Q7 Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).

Answer:

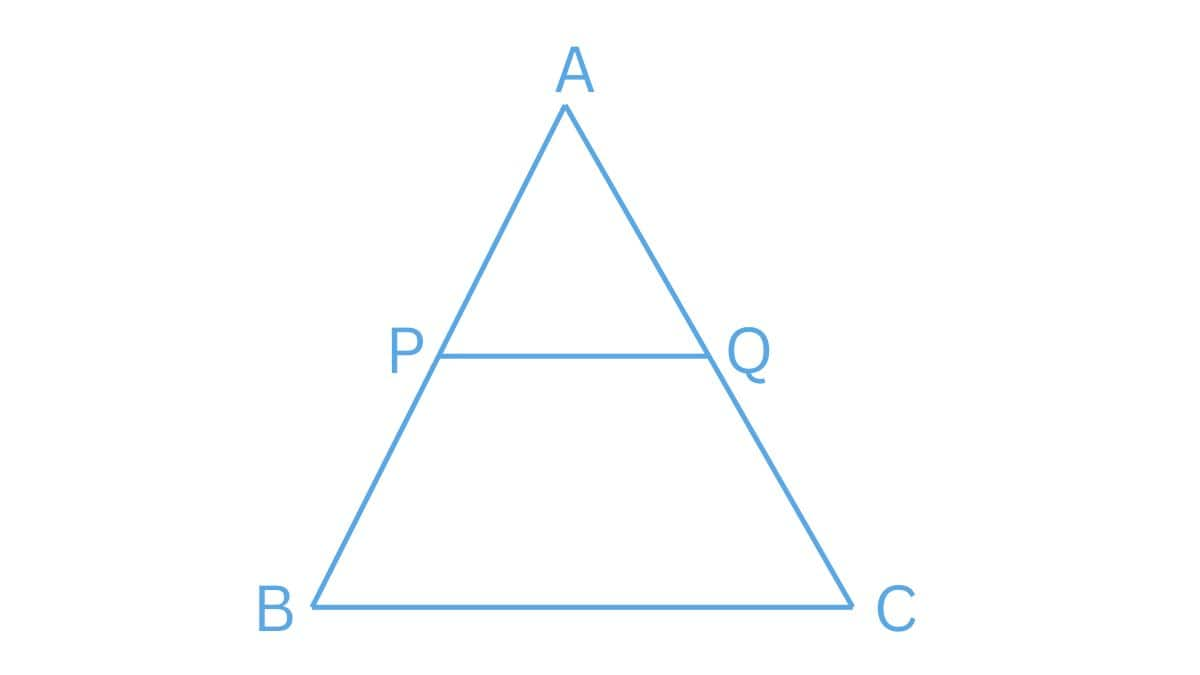
Let PQ be a line passing through the midpoint of line AB and parallel to line BC, intersecting line AC at point Q.

i.e. $PQ||BC$ and $AP=PB$ .

Using the basic proportionality theorem, we have

$\frac{AP}{PB}=\frac{AQ}{QC}.........(1)$

Since $AP=PB$

$\frac{AQ}{QC}=\frac{1}{1}$

$\Rightarrow AQ=QC$

$\therefore$ Q is the midpoint of AC.

Q8 Using Theorem 6.2, prove that the line joining the midpoints of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).

Answer:

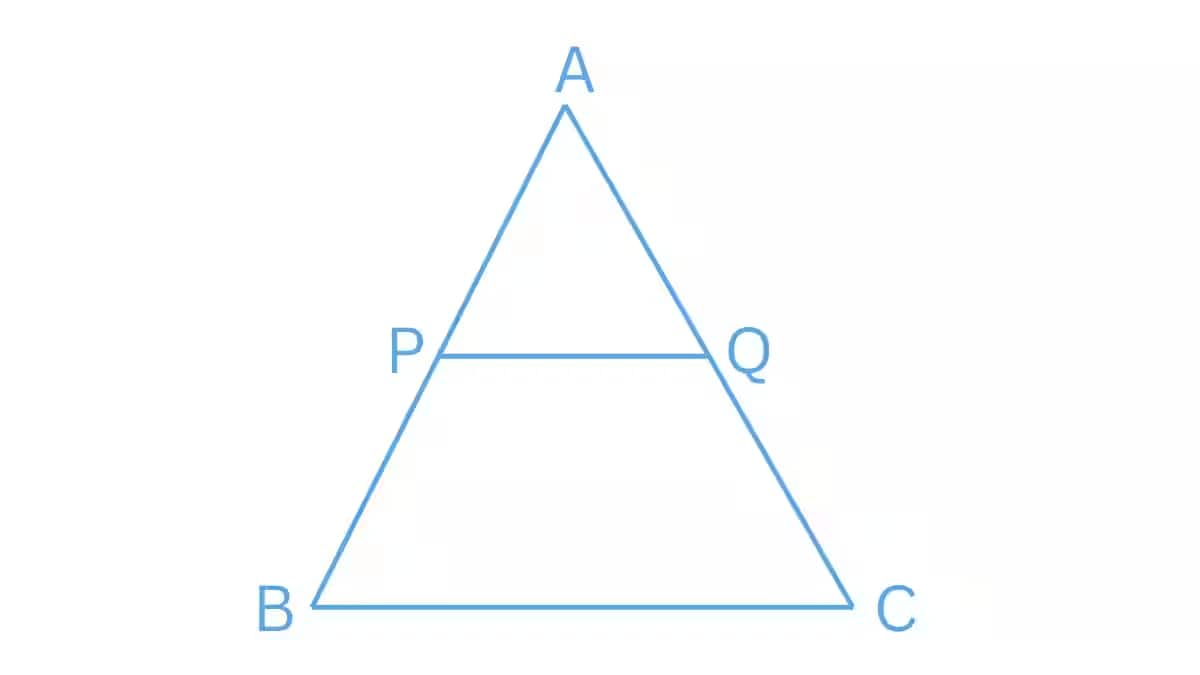
Let P is the midpoint of line AB, and Q is the midpoint of line AC.

PQ is the line joining midpoints P and Q of lines AB and AC, respectively.

i.e. $AQ=QC$ and $AP=PB$ .

We have,

$\frac{AP}{PB}=\frac{1}{1}..........................1$

$\frac{AQ}{QC}=\frac{1}{1}...................................2$

From equations (1) and (2), we get

$\frac{AQ}{QC}=\frac{AP}{PB}$

Therefore, by the basic proportionality theorem, we have $PQ||BC$

Q9 ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show
that $\frac{AO}{BO} = \frac{CO}{DO}$

Answer: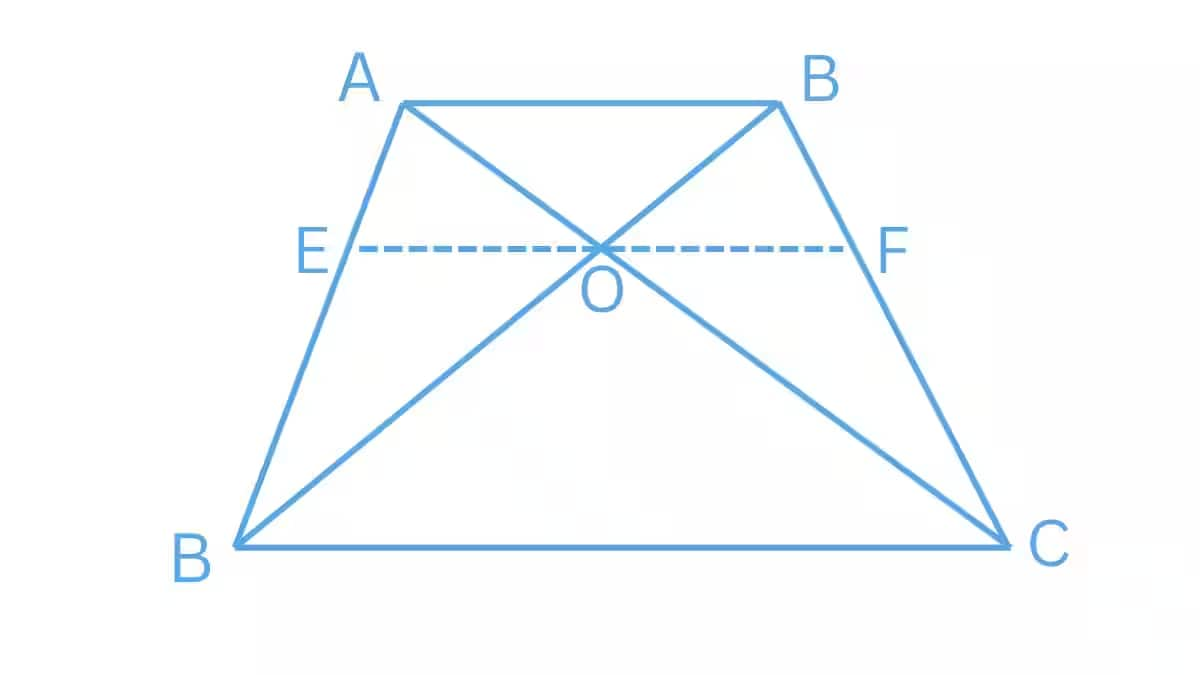

Draw a line EF passing through point O such that $EO||CD\, \, and\, \, FO||CD$

To prove:

$\frac{AO}{BO} = \frac{CO}{DO}$

In $\triangle ADC$ , we have $CD||EO$

So, by using the basic proportionality theorem,

$\frac{AE}{ED}=\frac{AO}{OC}........................................1$

In $\triangle ABD$ , we have $AB||EO$

So, by using the basic proportionality theorem,

$\frac{DE}{EA}=\frac{OD}{BO}........................................2$

Using equations (1) and (2), we get

$\frac{AO}{OC}=\frac{BO}{OD}$

$\Rightarrow \frac{AO}{BO} = \frac{CO}{DO}$

Hence proved.

Q10 The diagonals of a quadrilateral ABCD intersect each other at point O such that $\frac{AO}{BO} = \frac{CO}{DO}$ Show that ABCD is a trapezium.

Answer: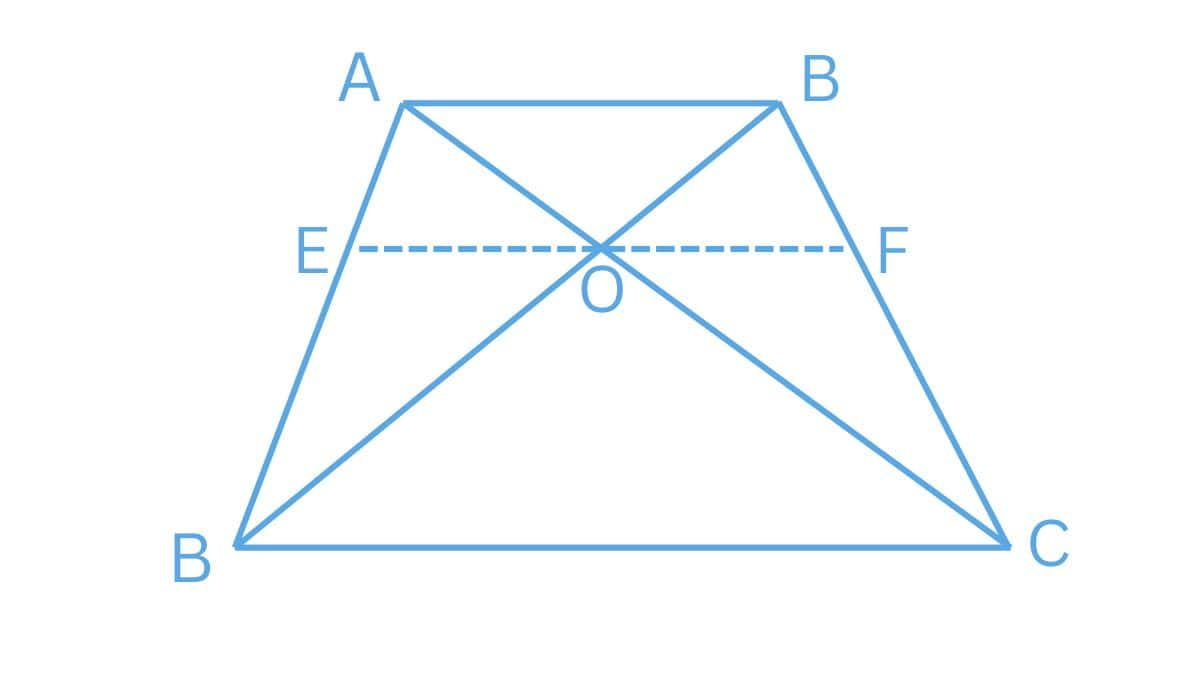

Draw a line EF passing through point O such that $EO||AB$

Given :

$\frac{AO}{BO} = \frac{CO}{DO}$

In $\triangle ABD$ , we have $AB||EO$

So, by using the basic proportionality theorem,

$\frac{AE}{ED}=\frac{BO}{DO}............(1)$

However, it is given that

$\frac{AO}{CO} = \frac{BO}{DO}.............(2)$

Using equations (1) and (2), we get

$\frac{AE}{ED}=\frac{AO}{CO}$

$\Rightarrow EO||CD$ (By basic proportionality theorem)

$\Rightarrow AB||EO||CD$

$\Rightarrow AB||CD$

Therefore, ABCD is a trapezium.