NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.2 - Triangles
Similarity of figures is a property that is used to compare figures. Two triangles are said to be similar if their corresponding sides are in equal ratio and if their corresponding angles are equal. If the corresponding sides of two triangles are equal, then these triangles are called equiangular triangles. In an equiangular triangle, the ratio of the corresponding sides of the two sides is always the same. This property of triangles follows from the basic proportionality theorem.
This Story also Contains
- Download Free PDF of NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.2
- Assess NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.2
- Topics Covered in Chapter 6, Triangles: Exercise 6.2
- NCERT Solutions Subject Wise
- Subject-Wise NCERT Exemplar Solutions

These NCERT solutions of Class 10 maths ex 6.2 contain two theorems: (Theorem 1) When a parallel line is drawn along one of the triangle's sides and intersects the other two sides at certain points, the two sides are divided in the same proportion. (Theorem 2) Any line that divides the two sides of a triangle in the same ratio is parallel to the third side. NCERT solutions for exercise 6.2 Class 10 Maths chapter 6 Triangles discuss the concept as per the NCERT Book, like a triangle as a polygon, the interior angles of a triangle, the exterior angles of a triangle, Pythagoras' theorem, and conditions of similarity in triangles.
Assess NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.2
Triangles Class 10 Chapter 6 Exercise: 6.2
Q1 In Fig. 6.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
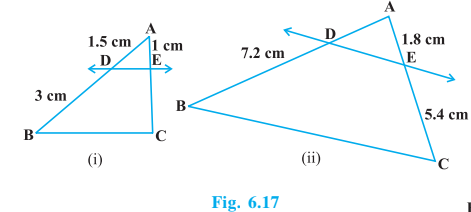
Answer:
(i)
Let EC be x
Given: DE || BC
By using the proportionality theorem, we get
$\frac{AD}{DB}=\frac{AE}{EC}$
$\Rightarrow \frac{1.5}{3}=\frac{1}{x}$
$\Rightarrow x=\frac{3}{1.5}=2\, cm$
$\therefore EC=2\, cm$
(ii)
Let AD be x
Given: DE || BC
By using the proportionality theorem, we get
$\frac{AD}{DB}=\frac{AE}{EC}$
$\Rightarrow \frac{x}{7.2}=\frac{1.8}{5.4}$
$\Rightarrow x=\frac{7.2}{3}=2.4\, cm$
$\therefore AD=2.4\, cm$
Answer:
(i)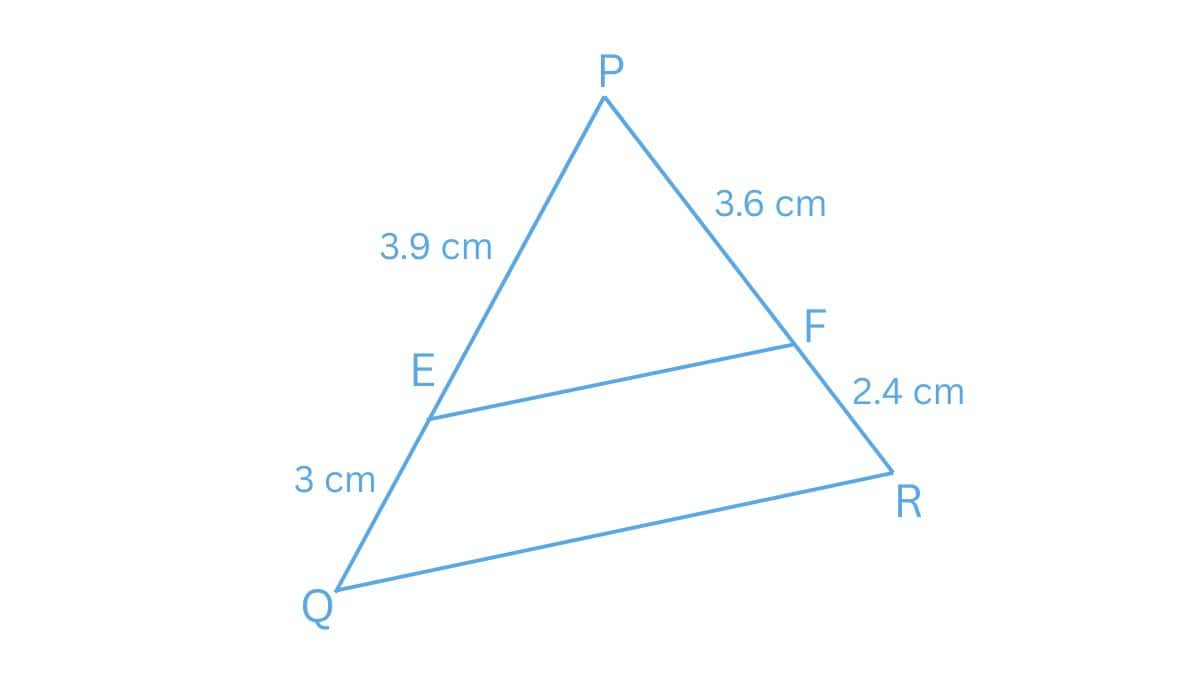
Given :
PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
$\frac{PE}{EQ}=\frac{3.9}{3}=1.3\, cm$ and $\frac{PF}{FR}=\frac{3.6}{2.4}=1.5\, cm$
We have
$\frac{PE}{EQ} \neq \frac{PF}{FR}$
Hence, EF is not parallel to QR.
Answer:
(ii)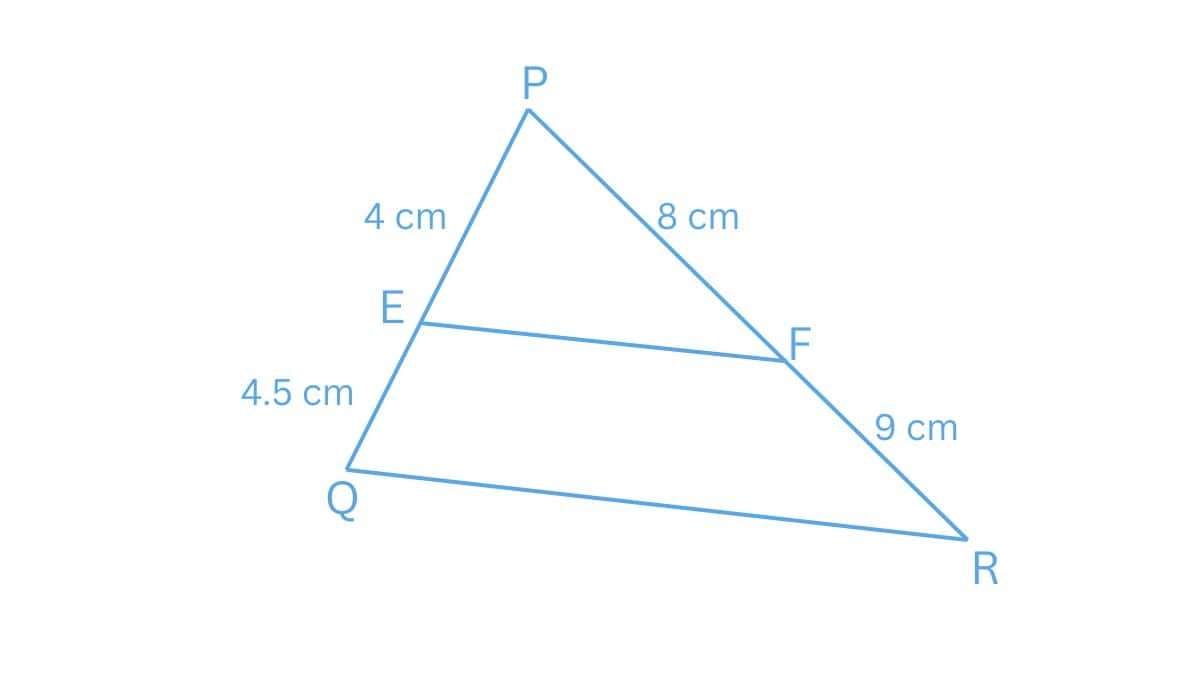
Given :
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
$\frac{PE}{EQ}=\frac{4}{4.5}=\frac{8}{9}\, cm$ and $\frac{PF}{FR}=\frac{8}{9}\, cm$
We have
$\frac{PE}{EQ} = \frac{PF}{FR}$
Hence, EF is parallel to QR.
Q2 (3) E and F are points on the sides PQ and PR respectively of a triangle PQR. For each of the following cases, state whether EF || QR : PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Answer:
(iii)
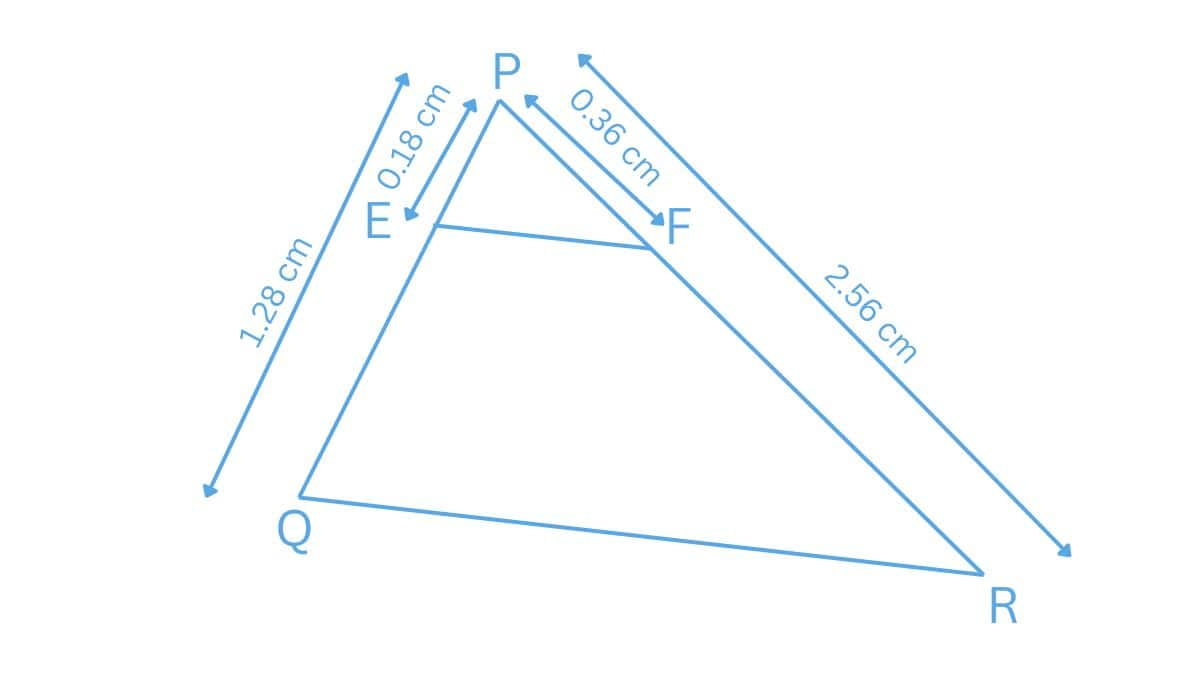
Given:
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
$\frac{PE}{PQ}=\frac{0.18}{1.28}=\frac{9}{64}\, cm$ and $\frac{PF}{PR}=\frac{0.36}{2.56}=\frac{9}{64}\, cm$
We have
$\frac{PE}{EQ} = \frac{PF}{FR}$
Hence, EF is parallel to QR.
Q3 In Fig. 6.18, if LM || CB and LN || CD, prove that $\frac{AM}{AB} = \frac{AN}{AD }$

Answer:
Given : LM || CB and LN || CD
To prove :
$\frac{AM}{AB} = \frac{AN}{AD }$
Since , LM || CB so we have
$\frac{AM}{AB}=\frac{AL}{AC}............(1)$
Also, LN || CD
$\frac{AL}{AC}=\frac{AN}{AD}..............(2)$
From equations 1 and 2, we have
$\frac{AM}{AB} = \frac{AN}{AD }$
Hence proved.
Q4 In Fig. 6.19, DE || AC and DF || AE. Prove that BF / FE = BE / EC
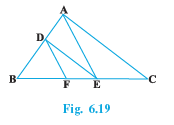
Answer:
Given: DE || AC and DF || AE.
To prove:
$\frac{BF}{FE} = \frac{BE}{EC }$
Since , DE || AC so we have
$\frac{BD}{DA}=\frac{BE}{EC}...........(1)$
Also, DF || AE
$\frac{BD}{DA}=\frac{BF}{FE}.............(2)$
From equations (1) and (2), we have
$\frac{BF}{FE} = \frac{BE}{EC }$
Hence proved.
Q5 In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.
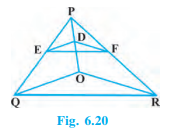
Answer:
Given: DE || OQ and DF || OR.
To prove EF || QR.
Since DE || OQ, we have
$\frac{PE}{EQ}=\frac{PD}{DO}..........(1)$
Also, DF || OR
$\frac{PF}{FR}=\frac{PD}{DO}.............(2)$
From equations (1) and (2), we have
$\frac{PE}{EQ} = \frac{PF}{FR }$
Thus, EF || QR. (Converse of the basic proportionality theorem)
Hence proved.
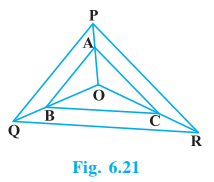
Answer:
Given: AB || PQ and AC || PR
To prove: BC || QR
Since, AB || PQ so we have
$\frac{OA}{AP}=\frac{OB}{BQ}............(1)$
Also, AC || PR
$\frac{OA}{AP}=\frac{OC}{CR}..............(2)$
From equations (1) and (2), we have
$\frac{OB}{BQ} = \frac{OC}{CR }$
Therefore, BC || QR. (converse basic proportionality theorem)
Hence proved.
Answer:
Let PQ be a line passing through the midpoint of line AB and parallel to line BC, intersecting line AC at point Q.
i.e. $PQ||BC$ and $AP=PB$ .
Using the basic proportionality theorem, we have
$\frac{AP}{PB}=\frac{AQ}{QC}.........(1)$
Since $AP=PB$
$\frac{AQ}{QC}=\frac{1}{1}$
$\Rightarrow AQ=QC$
$\therefore$ Q is the midpoint of AC.
Answer:
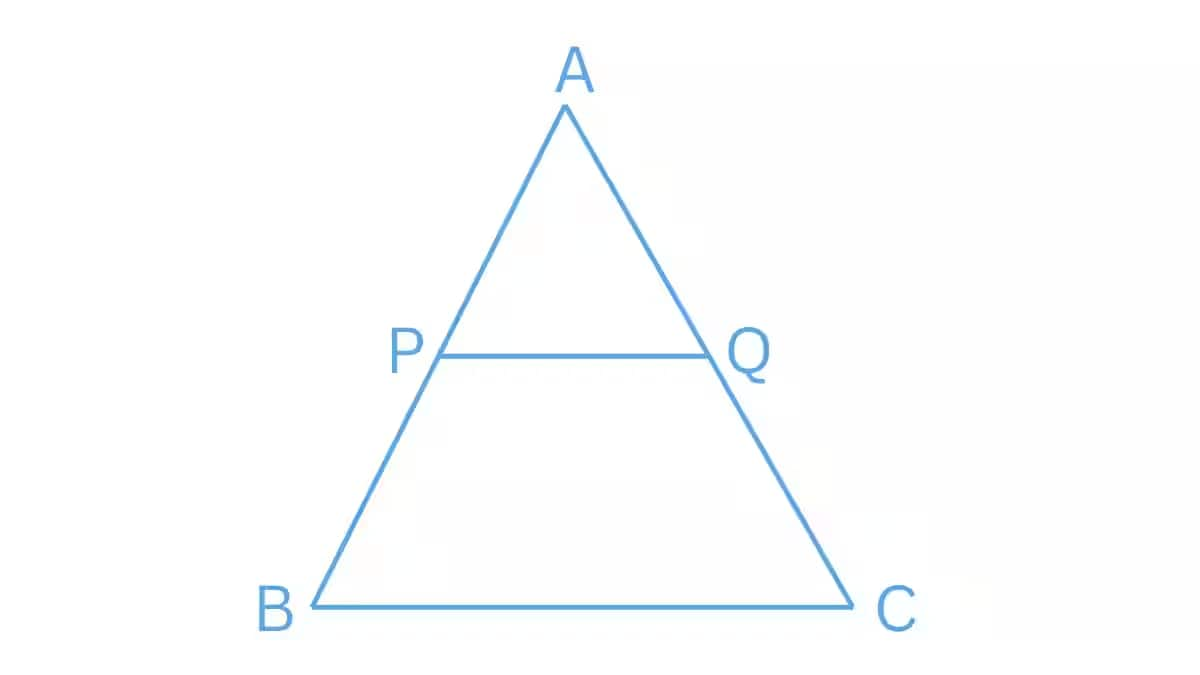
Let P is the midpoint of line AB, and Q is the midpoint of line AC.
PQ is the line joining midpoints P and Q of lines AB and AC, respectively.
i.e. $AQ=QC$ and $AP=PB$ .
We have,
$\frac{AP}{PB}=\frac{1}{1}..........................1$
$\frac{AQ}{QC}=\frac{1}{1}...................................2$
From equations (1) and (2), we get
$\frac{AQ}{QC}=\frac{AP}{PB}$
Therefore, by the basic proportionality theorem, we have $PQ||BC$
Answer: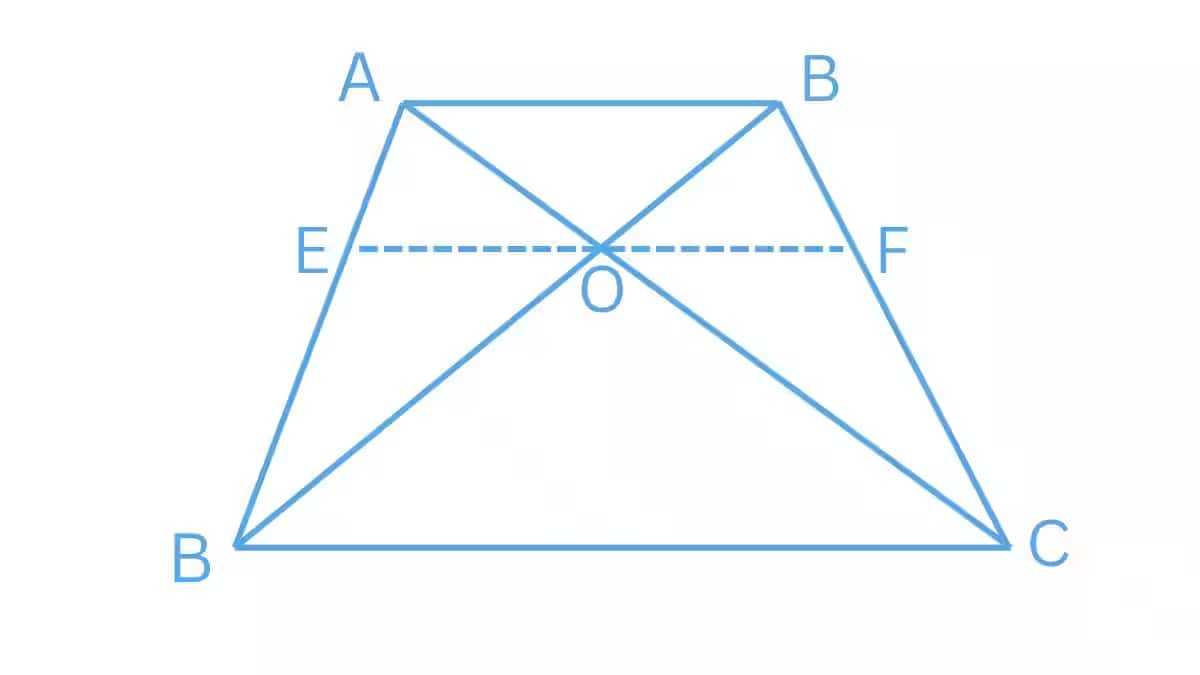
Draw a line EF passing through point O such that $EO||CD\, \, and\, \, FO||CD$
To prove:
$\frac{AO}{BO} = \frac{CO}{DO}$
In $\triangle ADC$ , we have $CD||EO$
So, by using the basic proportionality theorem,
$\frac{AE}{ED}=\frac{AO}{OC}........................................1$
In $\triangle ABD$ , we have $AB||EO$
So, by using the basic proportionality theorem,
$\frac{DE}{EA}=\frac{OD}{BO}........................................2$
Using equations (1) and (2), we get
$\frac{AO}{OC}=\frac{BO}{OD}$
$\Rightarrow \frac{AO}{BO} = \frac{CO}{DO}$
Hence proved.
Answer: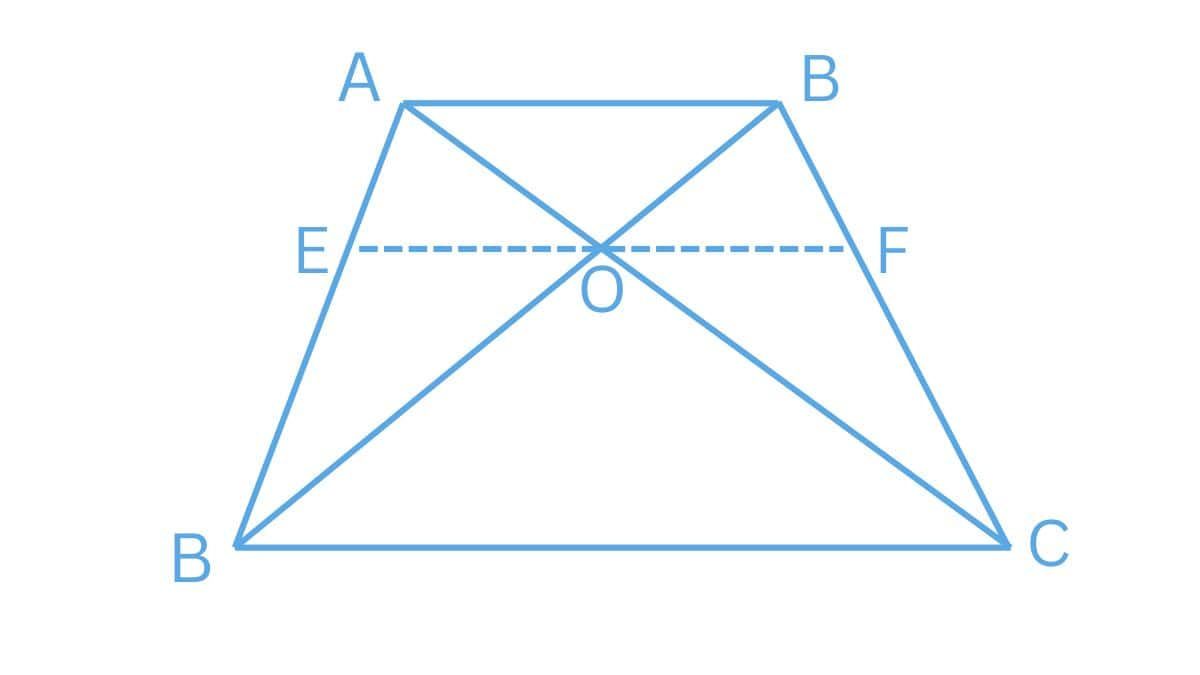
Draw a line EF passing through point O such that $EO||AB$
Given :
$\frac{AO}{BO} = \frac{CO}{DO}$
In $\triangle ABD$ , we have $AB||EO$
So, by using the basic proportionality theorem,
$\frac{AE}{ED}=\frac{BO}{DO}............(1)$
However, it is given that
$\frac{AO}{CO} = \frac{BO}{DO}.............(2)$
Using equations (1) and (2), we get
$\frac{AE}{ED}=\frac{AO}{CO}$
$\Rightarrow EO||CD$ (By basic proportionality theorem)
$\Rightarrow AB||EO||CD$
$\Rightarrow AB||CD$
Therefore, ABCD is a trapezium.
Also Read-
Topics Covered in Chapter 6, Triangles: Exercise 6.2
1. Similar Figures: Two figures are said to be similar if their corresponding sides are in the same proportion and corresponding angles are equal.
2. Conditions for Similar Triangles: The criteria for similarity of the triangle are AA (Angle-Angle), in which two angles of one triangle are equal to the corresponding two angles of another triangle.
3. Midpoint Theorem: In this theorem, the line segment that joins the midpoint of the two sides of the triangle is parallel to the third side of the triangle, and the length of this line segment is half of the third side of the triangle.
4. Parallel Lines and Transversals: A transversal divides the sides of the triangle into proportional segments when it intersects the two parallel lines.
Also see-
NCERT Solutions Subject Wise
Students must check the NCERT solutions for Class 10 Maths and Science given below:
Subject-Wise NCERT Exemplar Solutions
Students must check the NCERT exemplar solutions for Class 10 Maths and Science given below:
Frequently Asked Questions (FAQs)
The ratio of the areas of the triangles is equal to the square of the ratio of the sides.
Ratio of area = 1:4
4/x=1/3
x=12cm
The length of the longer side is 12cm.
It will always be parallel to the third side of the triangle.
The congruent figures are all similar, but the opposite is not true.
If we know the side ratio and the length of any side, we can find the length of the corresponding side of the other triangle by using the ratio.
The ratio of the areas of the triangles is equal to the square of the ratio of the sides.
No, resemblance only relates to the shape of the figures and does not imply equality.
The term "similar" refers to two figures that have the same shape but differ in size.
Questions related to CBSE Class 10th
On Question asked by student community
HELLO,
I am attaching the link through which you can download and access the Bangalore Sahodaya Class 10th CBSE question paper of Mathematics ( Basic )
Here is the link :- https://school.careers360.com/download/ebooks/bangalore-sahodaya-class-10-mathematics-basic-question-paper-2025-26
It will help you to practice basic level numerical questions, strengthen fundamentals and prepare confidently for the board
HELLO,
Below i am attaching the direct link of Careers360 through which you can download the Bangalore Sahodaya Class 10th Mathematics Basic Question paper 2025 2026
Here is the link :- https://school.careers360.com/download/ebooks/bangalore-sahodaya-class-10-mathematics-basic-question-paper-2025-26
Hope this will help you!
Hello
You will be able to download the CBSE Class 10th Maths Sample Paper 2025-26 using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-10th-maths-sample-papers-2025-26
I hope this information helps you.
Thank you.
Hello,
Here you can access the last 5 years CBSE Class 10 Board Exam Question Papers from the mentioned link below:
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers-class-10
Hope it helps.
You can check the Class 11 English half yearly question paper and answer key for 2025 26 on the Careers360 website. These papers help students practice, understand the exam pattern, and check their answers for better preparation.
You can visit this Careers360 link to access the English question paper and
Popular CBSE Class 10th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
