NCERT Solutions for Exercise 10.2 Class 10 Maths Chapter 10 - Circles

Q1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is

(A) 7 cm

(B) 12 cm

(C) 15 cm

(D) 24.5 cm

Answer:
The correct option is (A) = 7 cm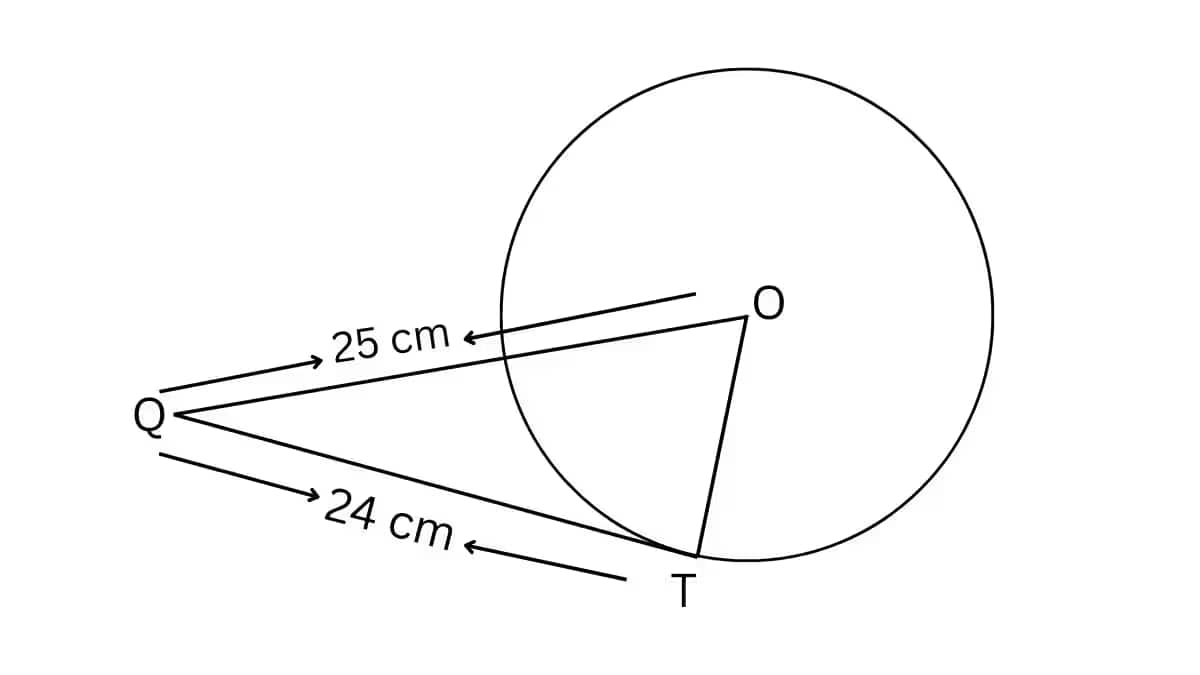

Given that,

The length of the tangent (QT) is 24 cm and the length of OQ is 25 cm.

Suppose the length of the radius OT be $l$ cm.

We know that $\mathrm{\Delta }OTQ$ is a right-angle triangle. So, by using Pythagoras' theorem-

$O{Q}^2=T{Q}^2+O{T}^2$

$l=\sqrt{{25}^2-{24}^2}$

$OT=l=\sqrt{49}$

OT = 7 cm

Q2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with center O so that $\mathrm{\angle }$ POQ = $110^{\circ }$, then $\mathrm{\angle }$ PTQ is equal to

(A) ${60}^{\circ }$

(B) ${70}^{\circ }$

(C) ${80}^{\circ }$

(D) $90^{\circ }$

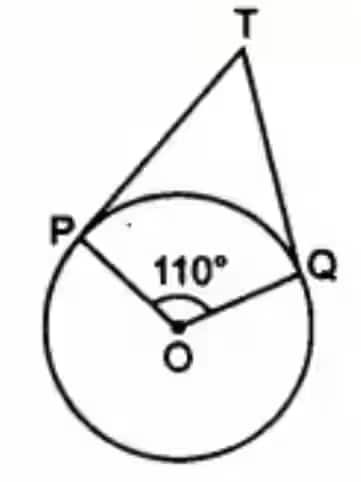
Answer:

The correct option is (b)

In figure, $\mathrm{\angle }POQ={110}^0$

Since POQT is quadrilateral. Therefore, the sum of the opposite angles is ${180}^0$

$\Rightarrow \mathrm{\angle }PTQ+\mathrm{\angle }POQ={180}^0$

$\Rightarrow \mathrm{\angle }PTQ={180}^0-\mathrm{\angle }POQ$

$={180}^0-{100}^0$

$={70}^0$

Q3. If tangents PA and PB from a point P to a circle with center O are inclined to each other at an angle of ${80}^{\circ }$, then $\mathrm{\angle }$ POA is equal to

(A) 50°

(B) 60°

(C) 70°

(D) 80°

Answer:
The correct option is (A)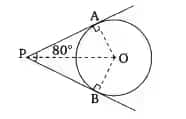

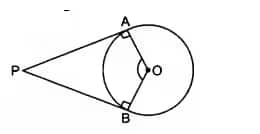
It is given that, tangents PA and PB from point P are inclined at $\mathrm{\angle }APB={80}^0$

In triangle $\mathrm{\Delta }$ OAP and $\mathrm{\Delta }$ OBP

$\mathrm{\angle }OAP=\mathrm{\angle }OBP={90}^0$

OA =OB (radii of the circle)

PA = PB (tangents of the circle)

Therefore, by SAS congruence

$\therefore \mathrm{\Delta }OAP\cong \mathrm{\Delta }OBP$

By CPCT, $\mathrm{\angle }OPA=\mathrm{\angle }OPB$

Now, $\mathrm{\angle }$ OPA = $\frac{80}{2}={40}^0$

In $\mathrm{\Delta }$ PAO,

$\mathrm{\angle }P+\mathrm{\angle }A+\mathrm{\angle }O=180$

$\mathrm{\angle }O={180}^0-{130}^0$

= ${50}^0$

Q4 Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

Answer: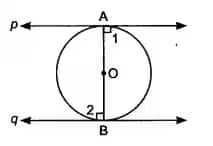

Let line $p$ and line $q$ be two tangents of a circle, and AB is the diameter of the circle.

OA and OB are perpendicular to the tangents $p$ and $q,$ respectively.

Therefore, $\mathrm{\angle }1=\mathrm{\angle }2={90}^0$

$\Rightarrow$ $p$ || $q$ ($\mathrm{\angle }$ $\because$ 1 & $\mathrm{\angle }$ 2 are alternate angles)

Q5 Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

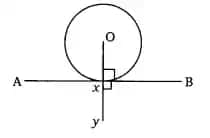
Answer:

In the above figure, the line AXB is the tangent to a circle with centre O. Here, OX is the perpendicular to the tangent AXB ( $OX\perp AXB$ ) at the point of contact X.

Therefore, we have,

$\mathrm{\angle }$ BXO + $\mathrm{\angle }$ YXB = ${90}^0+{90}^0={180}^0$

$\therefore$ OXY is collinear

$\Rightarrow$ OX is passing through the centre of the circle.

Q6 The length of a tangent from a point A at a distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Answer:

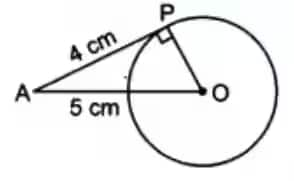
Given that,

The length of the tangent from the point A (AP) is 4 cm, and the length of OA is 5 cm.

Since $\mathrm{\angle }$ APO = 90⁰

Therefore, $\mathrm{\Delta }$ APO is a right-angle triangle. By using Pythagoras' theorem;

$O{A}^2=A{P}^2+O{P}^2$

$5^2=4^2+O{P}^2$

$OP=\sqrt{25-16}=\sqrt{9}$

$OP=3cm$

Q7 Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Answer:

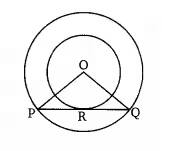
In the above figure, PQ is the chord to the larger circle, which is also tangent to a smaller circle at the point of contact R.

We have,

Radius of the larger circle OP = OQ = 5 cm

Radius of the small circle (OR) = 3 cm

OR $\perp$ PQ [since PQ is tangent to a smaller circle]

According to the question,

In $\mathrm{\Delta }$ OPR and $\mathrm{\Delta }$ OQR

$\mathrm{\angle }$ PRO = $\mathrm{\angle }$ QRO {both ${90}^0$ }

OR = OR {common}

OP = OQ {both radii}

By RHS congruence $\mathrm{\Delta }$ OPR $\cong$ $\mathrm{\Delta }$ OQR

So, by CPCT

PR = RQ

Now, In $\mathrm{\Delta }$ OPR,

By using Pythagoras' theorem,

$PR=\sqrt{25-9}=\sqrt{16}$

PR = 4 cm

Hence, PQ = 2.PR = 8 cm

Q8 A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC

Answer:

To prove- AB + CD = AD + BC

Proof-

We have,

Since the lengths of the tangents drawn from an external point to a circle are equal

AP =AS .......(I)

BP = BQ.........(ii)

AS = AP...........(iii)

CR = CQ ...........(iv)

By adding all the equations, we get;

$AP+BP+RD+CR=AS+DS+BQ+CQ$

$\Rightarrow (AP+BP)+(RD+CR)=(AS+DS)+(BQ+CQ)$

$\Rightarrow AB+CD=AD+BC$

Hence proved.

Q9 In Fig. 10.13, XY and X'Y'are two parallel tangents to a circle with center O and another tangent AB with a point of contact C intersecting XY at A and X'Y' at B. Prove that $\mathrm{\angle }$ AOB = 90°.

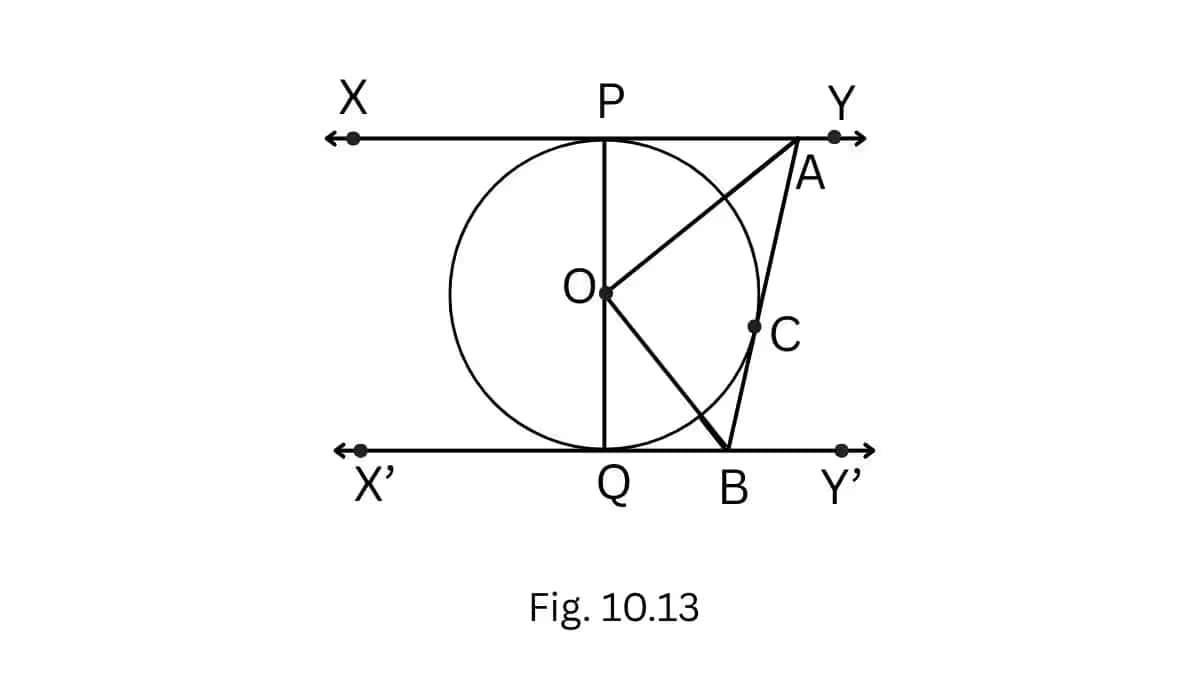
Answer:

To prove- $\mathrm{\angle }$ AOB = ${90}^0$

Proof-

In $\mathrm{\Delta }$ AOP and $\mathrm{\Delta }$ AOC,

OA =OA [Common]

OP = OC [Both radii]

AP =AC [tangents from external point A]

Therefore by SSS congruence, $\mathrm{\Delta }$ AOP $\cong$ $\mathrm{\Delta }$ AOC

And by CPCT, $\mathrm{\angle }$ PAO = $\mathrm{\angle }$ OAC

$\Rightarrow \mathrm{\angle }PAC=2\mathrm{\angle }OAC$ ..................(i)

Similarly, from $\mathrm{\Delta }$ OBC and $\mathrm{\Delta }$ OBQ, we get;

$\mathrm{\angle }$ QBC = 2. $\mathrm{\angle }$ OBC.............(ii)

Adding equations (1) and (2)

$\mathrm{\angle }$ PAC + $\mathrm{\angle }$ QBC = 180⁰

2( $\mathrm{\angle }$ OBC + $\mathrm{\angle }$ OAC) = 180⁰

( $\mathrm{\angle }$ OBC + $\mathrm{\angle }$ OAC) = 90⁰

Now, in $\mathrm{\Delta }$ OAB,

The sum of the interior angles is 180⁰.

So, $\mathrm{\angle }$ OBC + $\mathrm{\angle }$ OAC + $\mathrm{\angle }$ AOB = 180⁰

$\therefore$ $\mathrm{\angle }$ AOB = 90⁰

Hence proved.

Q10 Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.

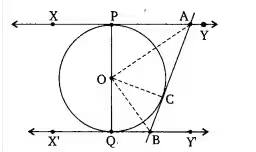
Answer:

To prove - $\mathrm{\angle }APB+\mathrm{\angle }AOB={180}^0$

Proof-

We have PA and PB are two tangents, and B and A are the points of contact of the tangents to a circle. And $OA\perp PA$ , $OB\perp PB$ (since tangents and radius are perpendiculars)

According to the question,

In quadrilateral PAOB,

$\mathrm{\angle }$ OAP + $\mathrm{\angle }$ APB + $\mathrm{\angle }$ PBO + $\mathrm{\angle }$ BOA = ${360}^0$

${90}^0$ + $\mathrm{\angle }$ APB + 90 + $\mathrm{\angle }$ BOA = ${360}^0$

$\mathrm{\angle }APB+\mathrm{\angle }AOB={180}^0$

Hence proved.

Q11 Prove that the parallelogram circumscribing a circle is a rhombus.

Answer: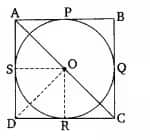

To prove - the parallelogram circumscribing a circle is a rhombus

Proof-

ABCD is a parallelogram that circumscribes a circle with centre O.

P, Q, R, and S are the points of contact on sides AB, BC, CD, and DA, respectively

AB = CD .and AD = BC...........(i)

It is known that tangents drawn from an external point are equal in length.

RD = DS ...........(ii)

RC = QC...........(iii)

BP = BQ...........(iv)

AP = AS .............(v)

By adding eq (ii) to eq (v) we get;

(RD + RC) + (BP + AP) = (DS + AS) + (BQ + QC)

CD + AB = AD + BC

$\Rightarrow$ 2AB = 2AD [from equation (i)]

$\Rightarrow$ AB = AD

Now, AB = AD and AB = CD

$\therefore$ AB = AD = CD = BC

Hence, ABCD is a rhombus.

Q12 A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC.


Answer:

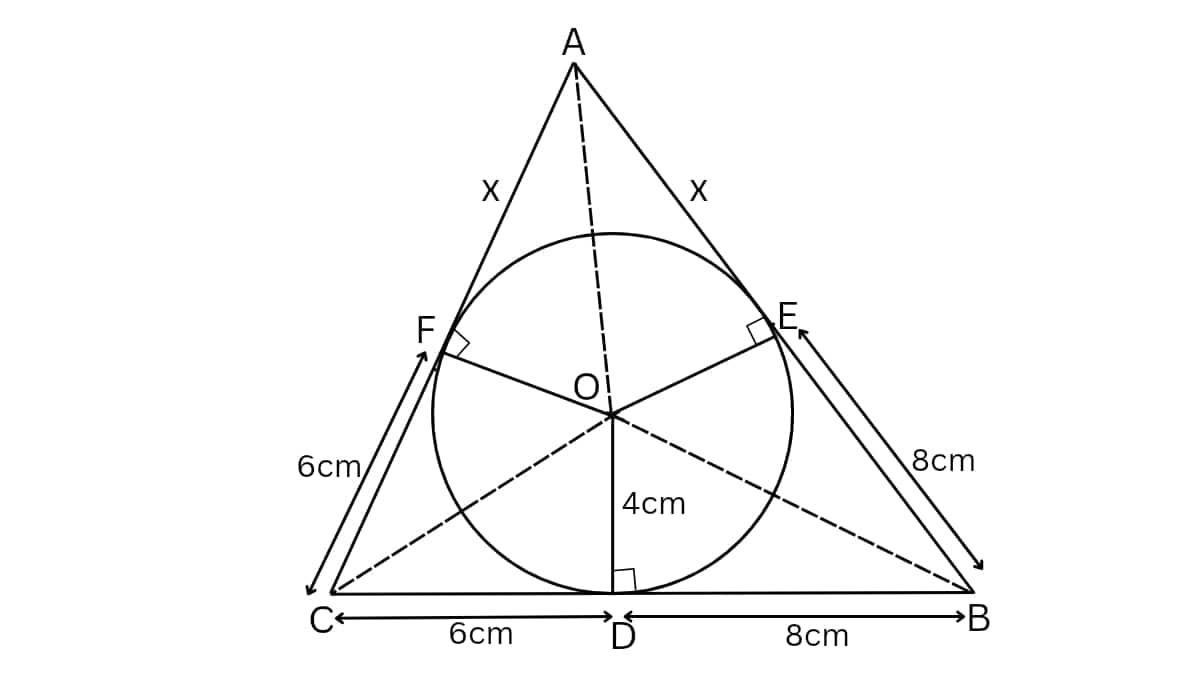
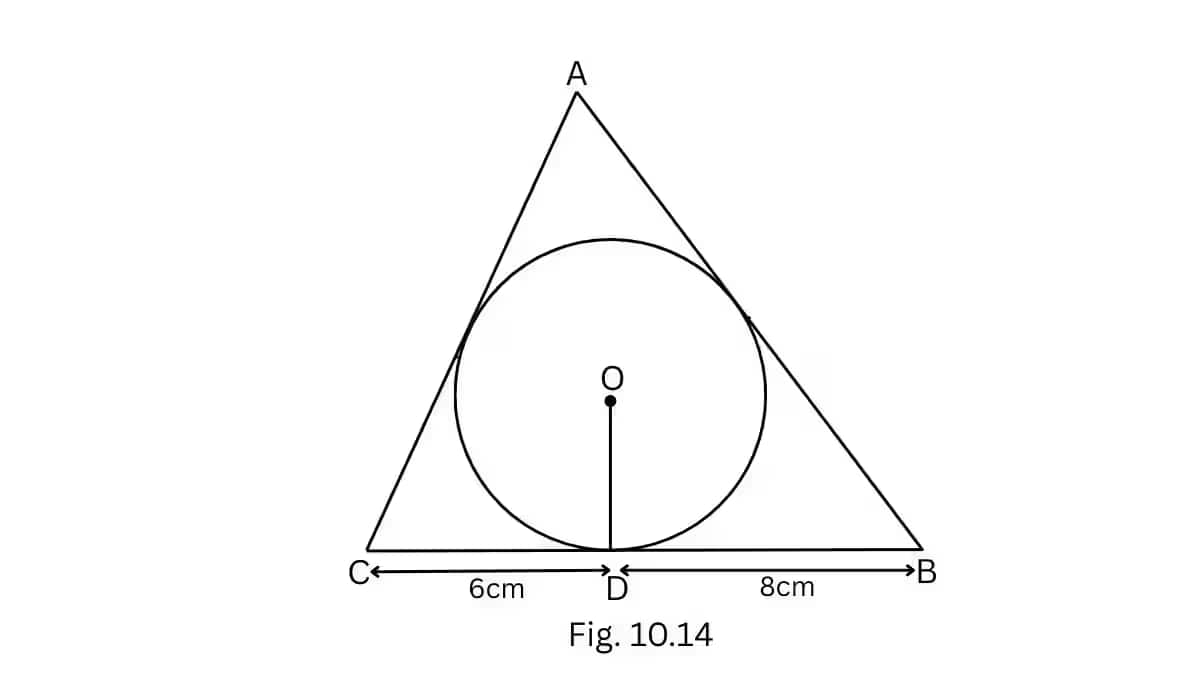
Consider the above figure. Assume centre O touches the sides AB and AC of the triangle at points E and F, respectively.

Let the length of AE is x.

Now in $△ABC$,

$CF=CD=6$ (tangents on the circle from point C)

$BE=BD=6$ (tangents on the circle from point B)

$AE=AF=x$ (tangents on the circle from point A)

Now, AB = AE + EB

$AB=AE+EB$

$=>AB=x+8$

$BC=BD+DC$

$=>BC=8+6=14$

$CA=CF+FA$

$=>CA=6+x$

Now,
$S=\frac{(AB+BC+CA)}{2}$

$=>S=\frac{(x+8+14+6+x)}{2}$

$=>S=\frac{(2x+28)}{2}$

$=>S=x+14$

Area of triangle $△ABC$

$=\sqrt{S\times (S-a)\times (S-b)\times (S-c)}$

$=\sqrt{(14+x)\times [(14+x)-14]\times [(14+x)-(6+x)]\times [(14+x)-(8+x)]}$

$=4\sqrt{3(14x+x^2)}$

Now the area of $△OBC$

$=(\frac{1}{2})\times OD\times BC$

$=(\frac{1}{2})\times 4\times 14$

$=\frac{56}{2}=28$

Area of $△OCA$

$=\frac{1}{2}\times OF\times AC$

$=\frac{1}{2}\times 4\times (6+x)$

$=2(6+x)$

$=12+2x$

Area of $△OAB$

$=\frac{1}{2}\times OE\times AB$

$=\frac{1}{2}\times 4\times (8+x)$

$=2(8+x)$

$=16+2x$

Now, Area of the $△ABC$ = Area of $△OBC$ + Area of $△OCA$ + Area of $△OAB$

$=>4\sqrt{3x(14+x)}$

$=28+12+2x+16+2x$

$=>4\sqrt{3x(14+x)}=56+4x$

$=>4\sqrt{3x(14+x)}=4(14+x)$

$=>\sqrt{3x(14+x)}]=14+x$

On squaring both sides, we get

$3x(14+x)=(14+x{)}^2$

$=>3x=14+x$ (14 + x = 0 => x = -14 is not possible)

$=>3x-x=14$

$=>2x=14$

$=>x=\frac{14}{2}$

$=>x=7$

Therefore,

$AB=x+8$

$=>AB=7+8$

$=>AB=15$

$AC=6+x$

$=>AC=6+7$

$=>AC=13$

Answer- AB = 15 and AC = 13

Q13 Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.

Answer: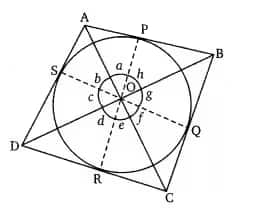

Given- ABCD is a quadrilateral circumscribing a circle. P, Q, R, and S are the points of contact on sides AB, BC, CD, and DA,

respectively.

To prove-

$$\begin{gathered} \mathrm{\angle }AOB+\mathrm{\angle }COD={180}^0 \\ \mathrm{\angle }AOD+\mathrm{\angle }BOC={180}^0 \end{gathered}$$

Proof -

Join OP, OQ, OR and OS

In triangle $\mathrm{\Delta }$ DOS and $\mathrm{\Delta }$ DOR,

OD =OD [common]

OS = OR [radii of same circle]

DR = DS [length of tangents drawn from an external point is equal ]

By SSS congruency, $\mathrm{\Delta }$ DOS $\cong$ $\mathrm{\Delta }$ DOR,

and by CPCT, $\mathrm{\angle }$ DOS = $\mathrm{\angle }$ DOR

$\mathrm{\angle }c=\mathrm{\angle }d$ .............(i)

Similarily,

$$\begin{gathered} \mathrm{\angle }a=\mathrm{\angle }b \\ \mathrm{\angle }e=\mathrm{\angle }f \\ \mathrm{\angle }g=\mathrm{\angle }h \end{gathered}$$ ...............(2, 3, 4)

$\therefore 2(\mathrm{\angle }a+\mathrm{\angle }e+\mathrm{\angle }h+\mathrm{\angle }d)={360}^0$

$$\begin{gathered} (\mathrm{\angle }a+\mathrm{\angle }e)+(\mathrm{\angle }h+\mathrm{\angle }d)={180}^0 \\ \mathrm{\angle }AOB+\mathrm{\angle }DOC={180}^0 \end{gathered}$$

SImilarily, $\mathrm{\angle }AOD+\mathrm{\angle }BOC={180}^0$

Hence proved.