NCERT solutions for Class 12 Physics Chapter 3 - Current Electricity
The NCERT Class 12 Physics Chapter 3 solutions of Current Electricity are made by subject experts to ensure that even the most difficult concepts can be easily understood. The solutions are very useful to students who are about to give CBSE Class 12 board exams as well as competitive exams such as the JEE and NEET, where accuracy and speed in problem-solving are paramount.
Candidates will have to ensure that the QR code and barcode are clearly visible on the JEE Main 2026 admit card at the time of download. On the exam day, candidates are required to carry the same photo ID that was uploaded during the application process and is mentioned on the admit card for identity verification.
This Story also Contains
- NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity: Download PDF
- NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity: Exercise Question
- NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity: Additional Questions
- Class 12 Physics NCERT Chapter 3: Higher Order Thinking Skills (HOTS) Questions
- Class 12 Physics Chapter 3 - Current Electricity: Important Topics
- Class 12 Physics Chapter 3 - Current Electricity: Important Formulas
- Approach to Solve Questions of Class 12 Physics Chapter 3 - Current Electricity
- How Can NCERT Solutions for Class 12 Physics Chapter 3 Current Electricity Help in Exam Preparation?
- Importance of NCERT Solutions for Class 12 Physics Chapter 3: Current Electricity
- What Extra Should Students Study Beyond NCERT for JEE/NEET?
- Class 12 Physics NCERT Solutions: Chapter- Wise

Throughout this chapter, the students will not only get step-by-step answers to all the NCERT exercise questions but also other questions and HOTS (Higher Order Thinking Skills) that will test their ability to think analytically and apply the concepts. Through these questions, the students would be in a position to attain a high level of conceptual clarity, which would be used to create the appropriate problem-solving strategy in exams. The NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity address important concepts including Ohm's Law and resistivity, Series and parallel combinations of resistors, Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL), Applications of Wheatstone Bridge and meter bridge and Internal resistance of cells, electrical power and energy. In addition to explanations, students will also be informed about the way to solve theory-based and numerical questions. This increases confidence, but also precision in exams. Frequent revision with these NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity will ensure the students can connect the theories covered in physics with practical and real-life applications of electricity, such as electric circuits, home wiring, and instruments and make the learning process more viable and exciting. Through these properly organised NCERT solutions, students are able to be well prepared, build their basics and achieve better marks in not only board but also entrance examinations.
NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity: Download PDF
The Class 12 Physics Chapter 3 - Current Electricity question answers PDF can be downloaded freely and thus exam preparation will be easy and more organised. Using this PDF, students are able to update stepwise solutions, practice numerical problems and go through key additional and HOTS questions any time and even without internet access. The downloadable class 12 physics chapter 3 Current Electricity questions answers, which are designed by subject experts, are a good study material for both CBSE board exams and regular JEE and NEET learners.
NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity: Exercise Question
The Current Electricity NCERT Solutions of Exercise Questions give step-by-step solutions to all the textbook problems, and even the difficult numerical problems were simplified. Such class 12 physics chapter 3 Current Electricity question answers not only add value to conceptual clarity but also help to increase both the speed and accuracy of problem-solving. They provide well-structured procedures and correct solutions that make them a good practice guide towards board examination of the CBSE and competitive exams such as JEE and NEET.
Answer :
Given the emf of the battery, E = 12 V
Internal resistance of battery, r = 0.4 Ohm
Let I be the maximum current drawn from the battery.
We know, according to Ohm's law
E = Ir
I = E/r = 12/0.4 =30 A
Hence, the maximum current drawn from the battery is 30 A.
Answer:
Given the emf of the battery, E = 10 V
The internal resistance of the battery, r = 3 Ohm
Current in the circuit, I = 0.5 A
Let R be the resistance of the resistor.
Therefore, according to Ohm's law:
E = IR' = I(R + r)
10 = 0.5(R + 3)
R = 1 Ohm
Also,
V = IR (Across the resistor)
= 0.5 x 17 = 8.5 V
Hence, the terminal voltage across the resistor = 8.5 V
3.3 At room temperature (27.0 °C), the resistance of a heating element is 100 Ω. What is the temperature of the element if the resistance is found to be 117 Ω, given that the temperature coefficient of the material of the resistor is 1.7 x 10-4 oC-1?
Answer:
Given,
temperature coefficient of filament,
α = 1.7 x 10-4 oC-1
$T_1= 27^\circ C$ ; $R_1 = 100 \Omega$
Let T2 be the temperature of the element, R2=117 Ω
(Positive alpha means that the resistance increases with temperature. Hence, we can deduce that T2 will be greater than T1.)
We know,
$R_2 = R_1[1 + \alpha \Delta T]$
$\implies$ $117 = 100[1 +(1.70\times 10^{-4})(T_2 - 27) ]$
$\\ \Rightarrow T_2-27=\frac{117-100}{1.7\times10^{-4}}\\$
$\Rightarrow T_2-27=1000\\\Rightarrow T_2=1027^\circ C$
Hence, the temperature of the element is 1027 °C.
Answer:
$R = \rho l/ A$ , where $\rho$ is the resistivity of the material
$\implies \rho = RA/l = 5 \times6\times10^{-7}/15$
$\implies \rho = 2\times10^{-7}$
Hence, the resistivity of the material of the wire is $\rho = 2\times10^{-7}\ ohm-m$
Answer:
Given,
$T_1= 27.5 ^\circ C$ ; $R_1 = 2.1\Omega$
$T_2= 100^\circ C$ ; $R_2= 2.7\Omega$
We know,
$R_2 = R_1[1 + \alpha \Delta T]$
2.7 = 2.1[1 + $\alpha$ (100 - 27.5) ]
$\alpha$ = (2.7 - 2.1) / 2.1(100 -27.5)
$\alpha$ = 0.0039 $^\circ C^{-1}$
Hence, the temperature coefficient of silver wire is 0.0039 $^\circ C^{-1}$
Answer:
For the given voltage, the two values of current will correspond to two different values of resistance, which will correspond to two different temperatures.
V = 230 V
$I_1= 3.2 A$ and $I_2 = 2.8 A$
Using Ohm's law:
$R_1 = 230/3.2 = 71.87\Omega$
and
$R_2= 230/2.8 = 82.14 \Omega$
$T_1= 27^\circ C$
Let $T_2$ be the steady temperature of the heating element.
We know,
$R_2 = R_1[1 + \alpha \Delta T]$
That is
230/2.8 = 230/3.2[1 + ( $1.70\times 10^{-4}$ ) ( T2 - 27) ]
T2 = (840.5 + 27) °C
Hence, the steady temperature of the element is 867.5 °C.
3.7 Determine the current in each branch of the network shown in Fig. 3.30:

Answer:
The current in the circuit is distributed like

where I1, I2, and I3 are the different currents through the shown branches.
Now, applying KVL in the loop
$10-I10-I_25-(I_2+I_3)10=0$
Also, we have $I=I_1+I_2$
So putting it in the KVL equation
$10-(I_1+I_2)10-I_25-(I_2+I_3)10=0$
$10-10I_1-10I_2-5I_2-10I_2-10I_3=0$
$10-10I_1-25I_2-10I_3=0$ .................................(1)
Now let's apply KVL in the loop involving I1, I2 and I3
$5I_2-10I_1-5I_3=0$ .................................(2)
Now, the third equation of KVL
$5I_3-5(I_1-I_3)+10(I_2+I_3)=0$
$-5I_1+10I_2+20I_3=0$ ..............................(3)
Now we have 3 equations and 3 variables, on solving we get
$I_1= \frac{4}{17}A$
$I_2= \frac{6}{17}A$
$I_3= \frac{-2}{17}A$
Now the total current
$I=I_1+I_2=\frac{4}{17}+\frac{6}{17}=\frac{10}{17}$
Answer:
Emf of battery, E = 8 V
Internal resistance of battery, r = 0.5 Ω
Supply Voltage, V = 120 V
The resistance of the resistor, R = 15.5 Ω
Let V' be the effective voltage in the circuit.
Now, V' = V - E
V' = 120 - 8 = 112 V
Now, the current flowing in the circuit is:
I = V' / (R + r)
$\implies I = \frac{112}{15.5 + 0.5} = 7 A$
Now, using Ohm’s Law:
Voltage across resistor R is v = IR
V = 7 x 15.5 = 108.5 V
Now, the voltage supplied, V = Terminal voltage of battery + V
$\therefore$ Terminal voltage of battery = 120 -108.5 = 11.5 V
The purpose of having a series resistor is to limit the current drawn from the supply.
Answer:
We know,
$I = neAv_d$
vd :drift Velocity = length of wire(l) / time taken to cover
$I = neA \frac{l}{t}$
by substituting the given values
$\implies$ t = 2.7 x 104 s
Therefore, the time required by an electron to drift from one end of a wire to its other end is $2.7\times 10^4$ s.
NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity: Additional Questions
The Current Electricity NCERT Solutions of Class 12 Physics are meant to be used in addition to the textbook exercises and are aimed at giving an extra practice on the topic to be understood further. Such questions challenge the reasoning, formula application, and clarity of concepts, and the students are exam-ready. With a regular solution, learners will be able to further prepare themselves to not only board exams but also entrance tests such as JEE and NEET.
Answer:
Given,
The surface charge density of Earth
$\rho$ = $10^{-9}C m^{-2}$
Current over the entire globe = 1800 A
Radius of earth, r = 6.37 x 106 m
$\therefore$ The surface area of earth A = $4\pi r^2$
A= $4\pi (6.37\times10^6 )^2$ = $5.09 \times 10^{14} m^2$
Now, charge on the earth's surface,
$q=\rho\times A$
Therefore,
$q=1005.09 \times 10^5 \mathrm{C}$
Let the time taken to neutralize earth surface be t
$\therefore$ Current I = q / t
t = 282.78 s.
Therefore, the time taken to neutralise the Earth's surface is 282.78 s
Answer:
Given,
There are 6 secondary cells.
Emf of each cell, E = 2 V (In series)
The internal resistance of each cell, r = 0.015 Ω (In series)
And the resistance of the resistor, R = 8.5 Ω
Let I be the current drawn in the circuit.
$I = \frac{nE}{R + nr}$
$\implies I = \frac{6(2)}{8.5 + 6(0.015)} = \frac{12}{8.59}$
$\implies$ I = 1.4 A
Hence current drawn from the supply is 1.4 A
Therefore, terminal voltage, V = IR = 1.4 x 8.5 = 11.9 V
Answer:
Given,
Emf , E = 1.9 V
Internal resistance, r =380 Ω
The maximum current that can drawn is I = E/r = 1.9/380 = 0.005 A
The motor requires a large value of current to start, and hence, this cell cannot be used for a car.
Answer:
We know,
$R = \rho l / A$
The wires have the same resistance and are of the same length.
Hence,
$\frac{\rho_{Al}}{A_{Al}} = \frac{\rho_{Cu}}{A_{Cu}}$
$\implies \frac{A_{Al}}{A_{Cu}} = \frac{\rho_{Al}}{\rho_{Cu}} = \frac{2.63}{1.73}$
Now, mass = Density x Volume = Density x Area x length
Taking the ratio of their masses for the same length
$\implies \frac{m_{Al}}{m_{Cu}} = \frac{d_{AL}A_{Al}}{d_{Cu}A_{Cu}} = \frac{2.7\times2.63}{8.9\times1.73} < 1$
Hence, $m_{Al} < m_{Cu}$
Therefore, for the same resistance and length, the aluminium wire is lighter.
Since aluminium wire is lighter, it is used in power cables.
5. What conclusion can you draw from the following observations on a resistor made of alloy manganin?
|
Current A |
Voltage V |
Current A |
Voltage V |
|
0.2 |
3.94 |
3.0 |
59.2 |
|
0.4 |
7.87 |
4.0 |
78.8 |
|
0.6 |
11.8 |
5.0 |
98.6 |
|
0.8 |
15.7 |
6.0 |
118.5 |
|
1.0 |
19.7 |
7.0 |
138.2 |
|
2.0 |
39.4 |
8.0 |
158.0 |
Answer:
The ratio of Voltage to current for the various values comes out to be nearly constant, which is around 19.7.
Hence, the resistor made of alloy manganin follows Ohm's law.
Answer:
The current flowing through the conductor is constant for a steady current flow.
Also, current density, electric field, and drift speed are inversely proportional to the area of cross-section. Hence, not constant.
Answer the following questions:
Answer:
No. Ohm’s law is not universally applicable to all conducting elements.
A semiconductor diode is such an example.
Answer the following questions
8. A low-voltage supply from which one needs high currents must have very low internal resistance. Why?
Answer:
Ohm's law states that: V = I x R
Hence, for a low voltage V, the resistance R must be very low for a high value of current.
Answer the following questions:
9. A high tension (HT) supply of, say, 6 kV must have a very large internal resistance. Why?
Answer:
A very high internal resistance is required for a high-tension supply to limit the current drawn for safety purposes.
10. Choose the correct alternative:
(a) Alloys of metals usually have (greater/less) resistivity than that of their constituent metals.
(b) Alloys usually have much (lower/higher) temperature coefficients of resistance than pure metals.
(c) The resistivity of the alloy manganin is nearly independent of/ increases rapidly with the increase of temperature.
(d) The resistivity of a typical insulator (e.g., amber) is greater than that of a metal by a factor of the order of ( $10^{22} / 10^{23}$ ).
Answer:
(a) Alloys of metals usually have greater resistivity than that of their constituent metals.
(b) Alloys usually have much lower temperature coefficients of resistance than pure metals.
(c) The resistivity of the alloy manganin is nearly independent of temperature.
(d) The resistivity of a typical insulator (e.g., amber) is greater than that of a metal by a factor of the order of 1022.
Answer:
To get maximum effective resistance, combine them in series. The effective resistance will be nR.
Answer:
To get minimum effective resistance, combine them in parallel. The effective resistance will be R/n.
11.(c) What is the ratio of the maximum to the minimum resistance?
Answer:
The ratio is nR/(R/n) = $n^2$
Answer:
We have equivalent resistance = 11/3
Let's break this algebraically so that we can represent it in terms of 1, 2 and 3
$\frac{11}{3}=\frac{9+2}{3}=3+\frac{2}{3}=3+\frac{1*2}{1+2}$
This expression is expressed in terms of 1, 2 and 3. Hence, we can make a circuit that consists only of 1 ohm, 2 ohms and 3 ohms and whose equivalent resistance is 11/3. that is :

Answer:
Connect a 2 Ω and a 3 Ω resistor in parallel and a 1 Ω resistor in series to it
Equivalent Resistance R = {1/(1/2 + 1/3)} + 1 = 6/5 + 1
R = 11/5 Ω
Answer:
1 Ω+2 Ω+3 Ω=6 Ω, so we will combine the resistances in series.
Answer:
Connect all three resistors in parallel.
Equivalent resistance is R = 1/(1/1 + 1/2 + 1/3) = (1x 2 x 3)/(6 + 3 + 2)
R = 6/11 Ω
13.(a) Determine the equivalent resistance of the networks shown in Fig.

Answer:
It can be seen that in every small loop resistor 1 ohm is in series with another 1 ohm resistor, and two 2-ohm resistors are also in series, and we have 4 loops.
The equivalent resistance of one loop is equal to the parallel combination of 2 ohms and 4 ohm that is
$Equivalent\ R_{loop}=\frac{2*4}{2+4}=\frac{8}{6}=\frac{4}{3}$
Now we have 4 such loops in series,
$Total\ Equivalent\ R_{loop}=\frac{4}{3}+\frac{4}{3}+\frac{4}{3}+\frac{4}{3}=\frac{16}{3}$
Hence equivalent resistance of the circuit is 16/3 ohms.
13.(b) Determine the equivalent resistance of the networks shown in Fig

Answer:
It can be seen that all 5 resistors are in series, so
Equivalent Resistance = R + R + R + R + R = 5R
Hence, equivalent resistance is 5R.

Answer:
First, let us find the equivalent of the infinite network,
let equivalent resistance = R'

From the figure, we can consider the box as a resistance of R.
Now, we can write,
equivalent resistance = R' =[( R')Parallel with (1)] + 1 + 1
$\frac{R'*1}{R'+1}+2=R'$
$R'+2R'+2=R'^2+R'$
$R'^2-2R'-2=0$
$R'=1+\sqrt{3},or1-\sqrt{3}$
Since resistance can never be negative, we accept
$R'=1+\sqrt{3}$
, We have calculated the equivalent resistance of an infinite network,
Now
Total equivalent resistance = internal resistance of the battery + equivalent resistance of the infinite network
= 0.5+1+1.73
=3.23 ohm
$V=IR$
$I=\frac{V}{R}=\frac{12}{3.23}=3.72A$
Hence current drawn from the 12V battery is 3.72 amperes.
(a) What is the value of $\epsilon$?

Answer:
Given
Maintained a constant emf of the standard cell = 1.02V, balanced point of this cell = 67.3cm
Now, when the standard cell is replaced by another cell with emf = $\varepsilon$, the balanced point for this cell = 82.3cm
Now, as we know the relation
$\frac{\varepsilon}{l} =\frac{E}{L}$
$\varepsilon =\frac{E}{L}*l=\frac{1.02}{67.3}*82.3=1.247V$
Hence, the emf of another cell is 1.247V.
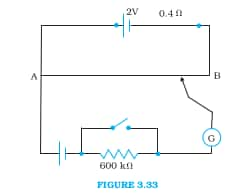
(b) What purpose does the high resistance of 600 k $\Omega$ have?

Answer:
If a sufficiently high current passes through the galvanometer, then it can get damaged. So we limit the current by adding a high resistance of 600 k $\Omega$.
(c) Is the balance point affected by this high resistance?

Answer:
No, the Balance point is not affected by high resistance. High resistance limits the current to the galvanometer wire. The balance point is obtained by moving the joystick on the potentiometer wire, and the current through the potentiometer wire is constant. The balance point is the point at which the current through the galvanometer becomes zero. The only duty of the high resistance is to supply a limited, constant current to the potentiometer wire.
Answer:
No, the method would not have worked if the driver cell of the potentiometer had an emf of 1.0V instead of 2, because when the emf of the driving point is less than that of the other cell, there won't be any balance point in the wire.
Answer:
No, the circuit would not work properly for a very low order of Voltage because the balance points would be near point A, and there would be a greater percentage error in measuring it. If we add a series resistance with wire AB. It will increase the potential difference of wire AB, which will lead to a decrease in percentage error.

Answer:
Given,
The balance point of the cell in an open circuit = $l_1=76.3cm$
value of external resistance added = $R=9.5\Omega$
new balance point = $l_2=64.8cm$
Let the internal resistance of the cell be $r$.
Now as we know, in a potentiometer,
$r=\frac{l_1-l_2}{l_2}*R$
$r=\frac{76.3-64.8}{64.8}*9.5=1.68\Omega$
Hence, the internal resistance of the cell will be 1.68 $\Omega$.
Class 12 Physics NCERT Chapter 3: Higher Order Thinking Skills (HOTS) Questions
The Class 12 Physics Chapter 3 HOTS (Higher Order Thinking Skills) questions on Current Electricity are designed to test deep conceptual understanding and analytical thinking. These questions go beyond direct textbook problems, encouraging students to apply concepts like Ohm’s Law, Kirchhoff’s Laws, and electrical circuits in new situations. Solving these helps students strengthen logical reasoning, improve problem-solving accuracy, and prepare effectively for competitive exams like JEE and NEET.
Q.1 The total current supplied to the circuit by the battery is

Answer:

The equivalent circuit is
The total resistance of the circuit is
$1.5+\frac{2 \times 6}{2+6}$ in parallel with $3 \Omega$
$\therefore$ Total resistance is $\frac{3}{2}=1.5 \Omega$
Current in the circuit $=\frac{6}{1.5}=4 \mathrm{~A}$
Q.2 What should be the value of E for which the galvanometer shows no deflection?
Answer:
If there is no current in G, as the potential difference across $10 \Omega$ resistance is equal to 10 V, then
$
\begin{aligned}
& \frac{\frac{10}{15}+\frac{E}{5}}{\frac{1}{15}+\frac{1}{15}}=10 \\
& \Rightarrow E=10 \mathrm{~V}
\end{aligned}
$
Q.3 A circuit consists of five identical conductors as shown in the figure. The two similar conductors are added as indicated by the dotted lines. The ratio of resistances before and after addition will be:
Answer:
Before addition,
Total resistance of the circuit is $\mathrm{R}_1=5 \Omega$
After the addition of the two conductors, the circuit will acquire the form shown in the figure
It is a balanced Wheatstone bridge. The resistance of the central conductor is ineffective.
$\therefore$ Total resistance of the circuit is
$
\begin{aligned}
& \mathrm{R}_2=1 \Omega+\frac{(2 \Omega)(2 \Omega)}{(2 \Omega+2 \Omega)}+1 \Omega=1 \Omega+1 \Omega+1 \Omega=3 \Omega \\
& \therefore \frac{\mathrm{R}_1}{\mathrm{R}_2}=\frac{5}{3}
\end{aligned}
$
Q.4 A current of $2A$ flows in the system of conductors as shown in the figure. The potential difference $V_P-V_R$ will be:
Answer:
Current through QRS = current through $\mathrm{}$ QPS=1$ \mathrm{}$ amp.
$
\begin{aligned}
& V_D-V_A=2 \times 1=2 \text { volt } \\
& V_D-V_B=3 \times 1=3 \text { volt } \\
& \therefore V_A-V_B=\left(V_D-V_B\right)-\left(V_D-V_A\right) \\
& =3-2 \\
& =1 \text { volt }
\end{aligned}
$
Q.5 In the network shown in the figure below, the potential difference between A and B is

Answer:
The distribution of current is shown in Fig. Keeping in view that the inflow and outflow of current in a cell must be the same. Applying the loop rule to left and right loops.

$\begin{aligned} & 2 \mathrm{i}_1+6 \mathrm{i}_1=4 \text { or } 2 \mathrm{i}_1=0.5 \mathrm{~A} \\ & 3 \mathrm{i}_1+1 \mathrm{i}_2=6 \text { or } \mathrm{i}_2=1.5 \mathrm{~A} \\ & \mathrm{~V}_{\mathrm{AB}}=\sum \mathrm{ir}-\sum e \\ & (=-2 \times 0.5+3 \times 1.5-4=-0.5 \mathrm{~V}) \\ & \mathrm{V}_{\mathrm{AB}}=-0.5 \mathrm{~V}\end{aligned}$
Class 12 Physics Chapter 3 - Current Electricity: Important Topics
Class 12 Physics Chapter 3 Current Electricity focuses on understanding how electric current flows in conductors and the factors affecting it. This chapter covers key topics like Ohm’s Law, resistance, resistivity, electric power, and combinations of resistors. Learning these concepts helps students build a strong base for both board exams and competitive exams such as JEE and NEET, where circuit-based questions are common.
3.1 Introduction
3.2 Electric Current
3.3 Electric Currents In Conductors
3.4 Ohm’S Law
3.5 Drift Of Electrons And The Origin Of Resistivity
3.5.1 Mobility
3.6 Limitations Of Ohm’S Law
3.7 Resistivity Of Various Materials
3.8 Temperature Dependence Of Resistivity
3.9 Electrical Energy, Power
3.10 Cells, Emf, Internal Resistance
3.11 Cells In Series And In Parallel
3.12 Kirchhoff’S Rules
3.13 Wheatstone Bridge
Class 12 Physics Chapter 3 - Current Electricity: Important Formulas
Class 12 Physics Chapter 3 Current Electricity includes several important formulas that help in solving circuit-related numerical problems. These formulas cover concepts like Ohm’s Law, resistors in series and parallel, electric power, and Kirchhoff’s laws. Understanding and applying these formulas correctly helps students solve questions quickly and accurately in board exams as well as competitive exams.
Current density:
1. $d i=J d A \cos \theta=\vec{J} \cdot d \vec{A}$
Where: is the angle between the normal to the area and the direction of the current
2. Relation between current density and electric field-
$\vec{J}=\sigma \vec{E}=\frac{\vec{E}}{\rho}$
where = conductivity and = resistivity or specific resistance of the substance
Ohm’s Law:
$\begin{aligned} & V \propto I \\ & V=I R\end{aligned}$
Resistivity:
$\rho=\frac{m}{n e^2 \tau}$
Where:
m is the mass, n is the number of electrons per unit volume, e is the charge of the electron and is the relaxation time
Grouping of Resistance:
1. Series Grouping of Resistance
$R_{e q}=R_1+R_2+\ldots \ldots \ldots+R_n$
2. Parallel Grouping of Resistance
$\frac{1}{R_{e q}}=\frac{1}{R_1}+\frac{1}{R_2}+\ldots \ldots \ldots . .+\frac{1}{R_n}$
Heat developed in a resistor:
The power developed $=\frac{\text { energy }}{\text { time }}=i^2 R=i R=\frac{V^2}{R}$
Kirchoff's Current Law(KCL):
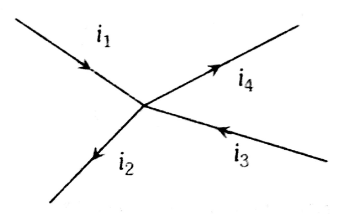
$
\sum i=0
$
$
i_1+i_3=i_2+i_4
$
Kirchoff's Voltage Law(KVL):
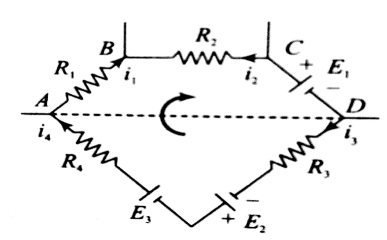
$\begin{aligned} & \sum V=0 \\ & -i_1 R_1+i_2 R_2-E_1-i_3 R_3+E_2+E_3-i_4 R_4=0\end{aligned}$
Wheatstone's Bridge:
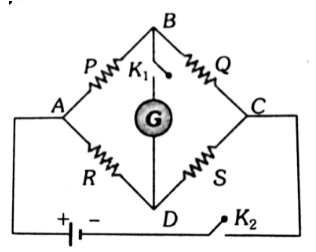
$\begin{aligned} & \frac{P}{Q}=\frac{R}{S} \\ & V_B=V_D(\text { Balanced condition })\end{aligned}$
Approach to Solve Questions of Class 12 Physics Chapter 3 - Current Electricity
Solving questions from Current Electricity requires a logical application of Ohm's Law, Kirchhoff's Laws, and resistor combinations. Instead of memorising, students should focus on understanding the flow of current and applying formulas strategically. A structured approach helps in solving numericals faster and with higher accuracy.
1. Know What Current Is:
Current is simply the flow of electric charge, such as water in a pipe. It flows due to a push named voltage.
2. Learn Ohm's Law(V=IR):
This states $V=I R$ (Voltage $=$ Current $\\times$ Resistance). It's the most important formula - used in the majority of questions.
3. Know About Resistance and Drift of Electrons
Electrons travel slowly in a wire - slow movement is referred to as drift. Resistance is determined by the material, length, and thickness of the wire.
4. Energy and Power:
Understand how to calculate energy and power consumed by devices such as bulbs or fans. Utilize formulas such as $P=$ $V I$ and $E=P t$.
5. Cells and EMF (Voltage):
Real batteries lose some energy within. That's internal resistance. Learn how to calculate total voltage with cells in series or parallel.
6. Kirchhoff's Rules:
These rules assist you in solving circuit problems. One is the current at junctions rule, and the other is the voltage in loops rule.
7. Wheatstone Bridge:
If the bridge is balanced, you can directly use a simple ratio formula to easily determine unknown resistance.
8. Practice NCERT Questions:
All questions of the board exam are based on the NCERT book mostly. Attempt all examples and exercises. Practice a few previous years' papers also.
How Can NCERT Solutions for Class 12 Physics Chapter 3 Current Electricity Help in Exam Preparation?
NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity help students develop a clear and logical understanding of how electric current flows through conductors and circuits. These solutions have made the explanations of the main concepts, including Ohm's law, resistance, resistivity, drift velocity, Kirchhoff's laws, and electrical power, more simplified in a series of explanations. Through the practice of numericals and derivations based on NCERT Solutions of Current Electricity, students will become confident enough with solving circuit-related problems in series and parallel combinations, Wheatstone bridge, and meter bridge that are generally tested in CBSE board examinations, JEE, and NEET. With repeated application of these solutions, accuracy is enhanced, frequent errors regarding the use of units and sign conventions are minimised, and problem-solving speed is enhanced. This concentrated study also provides a good base toward the subsequent chapters, such as Moving Charges and Magnetism and Electromagnetic Induction, which guarantees improved exam scores.
Importance of NCERT Solutions for Class 12 Physics Chapter 3: Current Electricity
NCERT Solutions for Class 12 Physics Chapter 3 - Current Electricity play a vital role in helping students master one of the most numerically-intensive chapters of Class 12 Physics. This chapter prepares the groundwork for the knowledge of electric circuits and the flow of current.
- Helps students gain a clear insight into fundamental concepts such as electric current, the law of Ohm, resistance, and resistivity.
- Explains important laws such as Kirchhoff's laws with proper reasoning and step-by-step solutions.
- Improves problem-solving with series and parallel combinations of circuits using detailed circuit-based numericals.
- Very crucial in CBSE board exams, whereby questions on derivations and numbericals in this chapter are often given.
- Highly useful for competitive exams like JEE and NEET, as current electricity forms the base for many higher-level questions.
- Helps students avoid common mistakes related to units, sign conventions, and circuit analysis.
- Prepares a good groundwork in the next chapters, like in Moving Charges and Magnetism and Electromagnetic Induction.
What Extra Should Students Study Beyond NCERT for JEE/NEET?
Class 12 Physics Chapter 3 - Current Electricity deals with the fundamental principles, such as Ohm's law, resistivity, combinations of resistors, Kirchhoff's rules, and the Wheatstone bridge. Nevertheless, in the case of JEE and NEET, students must not just use the textbook but concentrate on the higher-order applications like circuit solving with Kirchhoff's laws, network theorems, variations of Wheatstone bridges, and problems which involve the dependency of resistance on temperature. The main way to master this chapter to compete in exams is to practice difficult numerical problems and learn the real-life application of circuits.
Class 12 Physics NCERT Solutions: Chapter- Wise
The NCERT Solutions for Class 12 Physics are compiled in a chapter-wise format to make learning and revision simple. Each chapter link provides step-by-step solutions to textbook exercises, additional questions, HOTS, and key formulas. With these well-structured resources, students can prepare effectively for CBSE board exams as well as competitive exams like JEE and NEET.
Also, check the NCERT Books and NCERT Syllabus here:
- NCERT Books Class 12 Physics
- NCERT Syllabus Class 12 Physics
- NCERT Books Class 12
- NCERT Syllabus Class 12
Subject-wise solutions
- NCERT Solutions for Class 12 Mathematics
- NCERT Solutions for Class 12 Chemistry
- NCERT Solutions for Class 12 Physics
- NCERT Solutions for Class 12 Biology
Also, check
Frequently Asked Questions (FAQs)
In CBSE board exam, around 8 to 10% questions can be expected from the chapter Current Electricity. Certain papers of CBSE ask around 15% questions from NCERT chapter 3 Current Electricity. To score well in the exam follow NCERT syllabus and the exercise given in the NCERT Book. To practice more problems can refer to NCERT exemplar.
If we analyse the previous year NEET, JEE Main and board papers we can see that the topics like meter bridge, potentiometer and problems using kcl and kvl and combinations of resistance and cells are frequently asked.
In JEE main, 2 to 3 questions can be expected from the chapter on Current Electricity. The topics like Potentiometer, meter bridge, KVL and KCL are important.
The concepts in the current electricity chapter of NCERT Class 12 Physics are integral parts of NEET exam. Along with NCERT, practicing with previous year papers and mock tests would be enough.
Current electricity carries 8% of weightage on an average for NEET exam.
Current electricity is the basics of electrical and electronics engineering-related branches. In these branches, analysis and designs of the circuit are important and the basic laws studied in the Class 12 Physics Chapter 3 NCERT solutions help for the same.
Focus on understanding the key concepts, practising numerical problems, and solving previous year questions. Refer to NCERT solutions for detailed explanations and practice regularly.
Kirchhoff’s laws — Current Law (KCL) and Voltage Law (KVL) — help in analyzing complex electrical circuits. These laws are crucial for solving circuit problems, especially in JEE and NEET exams.
The Wheatstone Bridge and Potentiometer are important for measuring resistance and EMF in electrical circuits. They have a high weightage in competitive exams like JEE Main and NEET.
Drift velocity is small because electrons move slowly under the influence of an electric field, even though the electric signal propagates quickly.
Questions related to CBSE Class 12th
On Question asked by student community
Hello
You will be able to download the CBSE Previous Year Board Question Papers from our official website, careers360, by using the link given below.
https://school.careers360.com/boards/cbse/cbse-previous-year-question-papers
I hope this information helps you.
Thank you.
Hello
You will be able to download the CBSE Pre-Board Class 12 Question Paper 2025-26 from our official website by using the link which is given below.
https://school.careers360.com/boards/cbse/cbse-pre-board-class-12-question-paper-2025-26
I hope this information helps you.
Thank you.
Hello,
Yes, it's completely fine to skip this year's 12th board exams and give them next year as a reporter or private candidate, allowing you to prepare better; the process involves contacting your current school or board to register as a private candidate or for improvement exams during the specified
HELLO,
Yes i am giving you the link below through which you will be able to download the Class 12th Maths Book PDF
Here is the link :- https://school.careers360.com/ncert/ncert-book-for-class-12-maths
Hope this will help you!
Failing in pre-board or selection tests does NOT automatically stop you from sitting in the CBSE Class 12 board exams. Pre-boards are conducted by schools only to check preparation and push students to improve; CBSE itself does not consider pre-board marks. What actually matters is whether your school issues your
Popular CBSE Class 12th Questions
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters






