• School
  • Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
Principle Of Mathematical Induction Class 11th Notes - Free NCERT Class 11 Maths Chapter 4 notes - Download PDF

Principle Of Mathematical Induction Class 11th Notes - Free NCERT Class 11 Maths Chapter 4 notes - Download PDF

Edited By Ramraj Saini | Updated on Mar 22, 2022 04:43 PM IST

Class 11 Math chapter 4 notes are regarding Trigonometric functions. In chapter 4 we will be going through the Mathematical Induction concepts in Principle of Mathematical Induction Class 11 notes. This Class 11 Maths chapter 4 notes contains the following topics: Mathematical induction principles and a few examples.

JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy

Suggested: JEE Main: high scoring chapters | Past 10 year's papers

This Story also Contains
  1. NCERT Class 11 Math Chapter 4 Notes
  2. Significance of NCERT Class 11 Maths Chapter 4 Notes:
  3. NCERT Class 11 Notes Chapter Wise.

NCERT Class 11 Math chapter 4 notes also contain important formulas. NCERT Class 11 Math chapter 4 contains systematic explanations of topics using examples and exercises. NCERT Notes for Class 11 Math chapter 4 includes FAQ’s or frequently asked questions about the chapter. Every concept that is in CBSE Class 11 Maths chapter 4 notes is explained here in a simple and understanding way that can reach students easily.

All these concepts can be downloaded from Class 11 Maths chapter 4 notes pdf download, Principle of Mathematical Induction Class 11 notes, Class 11 Principle of Mathematical Induction notes pdf download.

Also, students can refer,

NCERT Class 11 Math Chapter 4 Notes

Mathematical Induction:

It is a mechanism, procedure, or technique to prove mathematical equations using a few principles. So as we use principles and solve these equations we call it the principles of mathematical induction.

3 steps to follow to solve using mathematical induction:

Let p(n) be a statement and n be a natural number:

Step 1 : (Basis Step)

L.H.S and R.H.S are equal for n=1 for given statement p(1).

Step 2 : (Introduction Step)

When the statement that is given is true for Assume(n=k), it should also be proved true for n=k+1 where we get LHS=RHS.

Step 3: (Conclusion Step)

Then we can state that proved Principles Of Mathematical Induction.

Let’s see an example:

Using the principles of mathematical induction prove the following statement :

1^2+2^2+3^2+4^2+..................+n^2 = \frac{n(n+1)(2n+1)}{6}

Ans:

Step 1:

Substitute n=1 in the given equation.

LHS= 1

RHS = n(n+1)(2n+1)/6 = 1 (1+1)(2(1)+1)/6 = 1 X 2 X 3/6 = 6/6 =1

Therefore LHS = RHS. Proved

Step 2:

Assume n=k for the given equation

Replace n with k

1^2+2^2+3^2+4^2+..................+k^2 = \frac{k(k+1)(2k+1)}{6}

Now we should prove it to be true for n=k+1

p(k+1)

Add (k+1)² on both sides of the equation

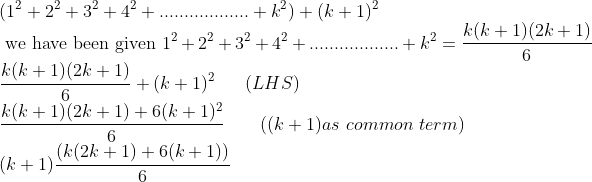
\\ (1^2+2^2+3^2+4^2+..................+k^2)+(k+1)^2 \\ \text{ we have been given} \ 1^2+2^2+3^2+4^2+..................+k^2 =\frac{k(k+1)(2k+1)}{6} \\ \frac{k(k+1)(2k+1)}{6} + (k+1)^2 \ \ \ \ \ ( LHS) \\ \frac{k(k+1)(2k+1)+6 (k+1)^2}{6} \ \ \ \ \ \ ( (k+1)as \ common \ term) \\ (k+1)\frac{(k(2k+1)+6 (k+1))}{6} \\

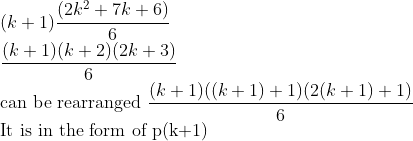
\\ (k+1) \frac{(2k^2+7k+6)}{6} \\ \frac{(k+1)(k+2)(2k+3)}{6} \\ \text{can be rearranged } \frac{(k+1)((k+1)+1)(2(k+1)+1)}{6} \\ \text{It is in the form of p(k+1)}

Hence proved from the principle of mathematical induction the given equation p(n) is true for n.

2. Using the principles of mathematical induction prove 7^n - 3^n is divisible by 4.

Ans:

Step 1:

Substitute n=1 in the given equation.

LHS = 7-3= 4 is divisible by 4.

LHS = RHS

Hence proved.

Step 2:

Assume n=k for the given equation

Replace n with k

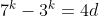7^k - 3^k =4d (d is some natural value)

Now we should prove it to be true for n=k+1

p(k+1)

Add (k+1) on both sides of the equation

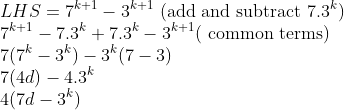
\\ LHS =7^{k+1}-3^{k+1} \ \text{(add and subtract } 7.3^k) \\ 7^{k+1}-7.3^k+7.3^k-3^{k+1} \text{( common terms)}\\ 7(7^k-3^k) - 3^k( 7-3)\\ 7( 4d) - 4. 3^k\\ 4( 7d - 3^k)

As it is multiple of 4. So divisible by 4.

p(k+1) is true for p(k) .

Hence proved from the principle of mathematical induction the given equation p(n) is true for n.

With this topic we conclude NCERT class 11 chapter 4 notes.

The link for the NCERT textbook pdf is given below:

URL: ncert.nic.in/textbook/pdf/kemh104.pdf

Significance of NCERT Class 11 Maths Chapter 4 Notes:

NCERT Class 11 Maths chapter 4 notes will be very much helpful for students to score maximum marks in their 11 board exams. In Principle of Mathematical Induction Class 11 chapter 4 notes, we have discussed many topics: Mathematical induction principles and a few examples. NCERT Class 11 Maths chapter 4 is also very useful to cover major topics of the Class 11 CBSE Maths Syllabus.

The CBSE Class 11 Maths chapter 4 will help to understand the formulas, statements, rules in detail. This pdf also contains previous year’s questions and NCERT textbook pdf. The next part contains FAQ’s or frequently asked questions along with topic-wise explanations. These topics can be obtained by the Principle of Mathematical Induction Class 11 chapter 4 pdf download.

NCERT Class 11 Notes Chapter Wise.

Subject Wise NCERT Exemplar Solutions

Subject Wise NCERT Solutions

JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBook

NCERT Books and Syllabus

NCERT Book for Class 11
NCERT Syllabus for Class 11

Also Read

Articles

Upcoming School Exams

Bihar Open Board 10th Examination

Application Date:11 November,2024 - 10 January,2025

Bihar Open Board 12th Examination

Application Date:11 November,2024 - 10 January,2025

National Means Cum-Merit Scholarship

Admit Card Date:27 November,2024 - 22 December,2024

Gujarat Board Higher Secondary School Certificate

Late Fee Application Date:13 December,2024 - 22 December,2024

Madhya Pradesh State Open School 10th Examination

Admit Card Date:13 December,2024 - 31 December,2024

View All School Exams
Get answers from students and experts

Popular Questions

A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is

Option 1)

0.34\; J

 Option 2)

0.16\; J
Option 3)

1.00\; J

 Option 4)

0.67\; J
Read More

A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times.  Assume that the potential energy lost each time he lowers the mass is dissipated.  How much fat will he use up considering the work done only when the weight is lifted up ?  Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate.  Take g = 9.8 ms−2 :

Option 1)

2.45×10−3 kg

 Option 2)

 6.45×10−3 kg
Option 3)

 9.89×10−3 kg

 Option 4)

12.89×10−3 kg

 
Read More

An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range

Option 1)

2,000 \; J - 5,000\; J

 Option 2)

200 \, \, J - 500 \, \, J
Option 3)

2\times 10^{5}J-3\times 10^{5}J

 Option 4)

20,000 \, \, J - 50,000 \, \, J
Read More

A particle is projected at 600   to the horizontal with a kinetic energy K. The kinetic energy at the highest point

Option 1)

K/2\,

 Option 2)

\; K\;
Option 3)

zero\;

 Option 4)

K/4
Read More

In the reaction,

2Al_{(s)}+6HCL_{(aq)}\rightarrow 2Al^{3+}\, _{(aq)}+6Cl^{-}\, _{(aq)}+3H_{2(g)}

Option 1)

11.2\, L\, H_{2(g)}  at STP  is produced for every mole HCL_{(aq)}  consumed

 Option 2)

6L\, HCl_{(aq)}  is consumed for ever 3L\, H_{2(g)}      produced
Option 3)

33.6 L\, H_{2(g)} is produced regardless of temperature and pressure for every mole Al that reacts

 Option 4)

67.2\, L\, H_{2(g)} at STP is produced for every mole Al that reacts .
Read More

How many moles of magnesium phosphate, Mg_{3}(PO_{4})_{2} will contain 0.25 mole of oxygen atoms?

Option 1)

0.02

 Option 2)

3.125 × 10-2
Option 3)

1.25 × 10-2

 Option 4)

2.5 × 10-2
Read More

If we consider that 1/6, in place of 1/12, mass of carbon atom is taken to be the relative atomic mass unit, the mass of one mole of a substance will

Option 1)

decrease twice

 Option 2)

increase two fold
Option 3)

remain unchanged

 Option 4)

be a function of the molecular mass of the substance.
Read More

With increase of temperature, which of these changes?

Option 1)

Molality

 Option 2)

Weight fraction of solute
Option 3)

Fraction of solute present in water

 Option 4)

Mole fraction.
Read More

Number of atoms in 558.5 gram Fe (at. wt.of Fe = 55.85 g mol-1) is

Option 1)

twice that in 60 g carbon

 Option 2)

6.023 × 1022
Option 3)

half that in 8 g He

 Option 4)

558.5 × 6.023 × 1023
Read More

A pulley of radius 2 m is rotated about its axis by a force F = (20t - 5t2) newton (where t is measured in seconds) applied tangentially. If the moment of inertia of the pulley about its axis of rotation is 10 kg m2 , the number of rotations made by the pulley before its direction of motion if reversed, is

Option 1)

less than 3

 Option 2)

more than 3 but less than 6
Option 3)

more than 6 but less than 9

 Option 4)

more than 9
Read More

Colleges After 12th

Popular Course After 12th

Applications for Admissions are open.

JEE Main Important Physics formulas
Apply

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

JEE Main Important Chemistry formulas
Apply

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

TOEFL ® Registrations 2024
Apply

Accepted by more than 11,000 universities in over 150 countries worldwide

Pearson | PTE
Apply

Register now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally

JEE Main high scoring chapters and topics
Apply

As per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE

JEE Main Important Mathematics Formulas
Apply

As per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters

View All Application Forms
News and Notifications
Kerala Class 7 student bitten by snake in classroom; Govt orders probe
Haryana schools to remain shut today in view of ex-CM Chautala's demise
Odisha: 14-year-old student stabs classmate in school; motive unknown
Class 10 student dies by suicide; parents allege harassment from teachers, peers
Winter vacation for Delhi schools from January 1 to 15; DoE issues guidelines for remedial class
Several Delhi schools receive bomb-threat mail, no suspicious items found
CBSE conducts surprise inspections at 29 schools; most violated board’s affiliation by-laws
Back to top