JEE Main Important Physics formulas
ApplyAs per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
Mathematical Reasoning Class 11th Notes - Free NCERT Class 11 Maths Chapter 14 notes - Download PDF
Edited By Ramraj Saini | Updated on Mar 22, 2022 05:35 PM IST
Notes for Class 11 Maths chapter 14 are regarding mathematical reasoning. In chapter 14 we will be going through the truth values concepts in Mathematical Reasoning Class 11 notes. This Class 11 Maths chapter 14 notes contains the following topics: sentence, compound sentence, connectives like the conjunction, disjunction, implication, biconditional, negation, contrapositive, converse, inverse, validation.
JEE Main Scholarship Test Kit (Class 11): Narayana | Physics Wallah | Aakash | Unacademy
Suggested: JEE Main: high scoring chapters | Past 10 year's papers
This Story also Contains
- NCERT CLASS 11 CHAPTER 14 NOTES
- Simple Statements:
- Compound Statements:
- Connectives:
- Quantifiers:
- Validity of Statements:
- Significance of NCERT Class 11 Maths Chapter 14 Notes:
- NCERT Class 11 Notes Chapter Wise.
NCERT Class 11 Math chapter 14 notes contain. NCERT Class 11 Math chapter 14 contains a detailed explanation of topics- Simple statements, Compound Statements, Connectives, Negation, Conjunction, Disjunction, Implications, Biconditional, Contrapositive, Converse, Inverse, Quantifiers. NCERT Notes for Class 11 Math chapter 14 is a detailed explanation of the chapter. It also contains FAQ’s that are frequently asked questions by students which can clarify many doubts of them. Every concept that is in CBSE Class 11 Maths chapter 14 notes is explained here in a simple way. All these concepts can be downloaded from Class 11 Maths chapter 14 notes pdf download, Mathematical Reasoning class 11 notes, Class 11 Mathematical Reasoning notes pdf download.
Also, students can refer,
- NCERT Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning
- NCERT Exemplar Class 11 Maths Chapter 14 Mathematical Reasoning
NCERT CLASS 11 CHAPTER 14 NOTES
A statement is a sentence that can either be true or false but not both at the same time.
Eg: 4 is greater than 10.
Even though it is false as it gives either true or false is a statement.
A sentence cannot be a statement when :
i) if it is an exclamation
Eg: Wow! It is so beautiful. (is not a statement)
ii) if it is a question
Eg: How are you? (is not a statement)
iii) if it is a command or request
Eg: Please get me a glass of water. (is not a statement)
Simple Statements:
Statements that are not further divided into two or more sentences are called Simple sentences.
Compound Statements:
Statements that can be further divided into two or more sentences are called Compound sentences.
They are generally joined using “and’, “or”.
Eg: 2 is an even number.
2 is a prime number.
Compound Sentence: 2 is both an even and a prime number.
Connectives:
Negation:
It is basically the opposite of the given statement.
If P is a given statement then the negation of a statement is denoted as ¬P.
Eg: Potatoes are my favorite vegetables. (statement)
Negation: Potatoes are not my favorite vegetables.
TRUTH TABLE:
P | ¬P |
T | F |
F | T |
Conjunction:
JEE Main Highest Scoring Chapters & Topics
Just Study 40% Syllabus and Score upto 100%
Download EBookThe statements p and q are joined using “and” form a compound statement then p and q are the conjunctions.
This is denoted using symbol:∧
Eg:
He likes tea.
He likes coffee.
Conjunction:
He likes both tea and coffee.
TRUTH TABLE:
p | q | p∧q |
T | T | T |
T | F | F |
F | T | F |
F | F | F |
Disjunction:
The statements p and q are joined using “or” that form a compound statement then p and q are the disjunctions.
This is denoted using symbol: ∨
Eg: He likes tea or he likes coffee.
TRUTH TABLE:
p | q | p∨q |
T | T | T |
T | F | T |
F | T | T |
F | F | F |
Implications:
The statements that use “if-then” or “only then” to form compound sentences are called implications.
It is denoted by symbol: → or ⇒
Eg: If you work hard then you can pass the exam.
TRUTH TABLE:
p | q | p⇒q |
T | T | T |
T | F | F |
F | T | T |
F | F | T |
Biconditional:
If two sentences are joined using “if and only if”
Then such statements are called biconditional statements.
Denoted using the symbol: ↔ or ⇔
TRUTH TABLE:
p | q | p⇔q |
T | T | T |
T | F | F |
F | T | F |
F | F | T |
Contrapositive:
If two statements are reversed and then negated under implication conditions then such statements are contrapositive statements.
TRUTH TABLE:
p | q | ¬q⇒¬p |
T | T | T |
T | F | F |
F | T | T |
F | F | T |
Converse:
The reverse of implication statements gives us the converse statements.
TRUTH TABLE:
p | q | q⇒p |
T | T | T |
T | F | T |
F | T | F |
F | F | T |
Inverse:
Negation of implication conditions is called inverse statements.
TRUTH TABLE:
p | q | ¬p⇒¬q |
T | T | T |
T | F | T |
F | T | F |
F | F | T |
Quantifiers:
We have two types of quantifiers.
Universal Quantifiers: These quantifiers are those that are suitable for all values.
We use words like “for all” and “for every.”
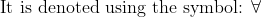
Existential Quantifiers: These are quantifiers that are used or satisfying for only a few particular values.
We use words like “there exists”.
It is denoted by the symbol:∃
Validity of Statements:
Validity is known from the values if they are true or false.
“p and q” are true if we have only both p and q are true.
“p or q “ is true when both p and q are true or anyone among p and q is true.
“p if q” is true only if p and q both are true or if p is false and q is true or if p and q both are false.
With this topic we conclude NCERT Class 11 chapter 14 notes.
The link for NCERT textbook pdf is given below:
URL: ncert.nic.in/textbook/pdf/kemh114.pd
Significance of NCERT Class 11 Maths Chapter 14 Notes:
NCERT Class 11 Maths chapter 14 notes will be very much helpful for students to score maximum marks in their 11 board exams. In Mathematical reasoning Class 11 chapter 14 notes we have discussed many topics: sentence, compound sentence, connectives like: conjunction, disjunction, implication, biconditional, negation, contrapositive, converse, inverse, validation, and truth tables. NCERT Class 11 Maths chapter 14 is also very useful to cover major topics of Class 11 CBSE Maths Syllabus.
The CBSE Class 11 Maths chapter 14 will help to understand the chapter in details. Students can get the document from Mathematical Reasoning class11 chapter 14 pdf download.
NCERT Class 11 Notes Chapter Wise.
NCERT Class 11 Maths Chapter 14 Notes |
Subject Wise NCERT Exemplar Solutions
- NCERT Exemplar Class 11 Solutions
- NCERT Exemplar Class 11 Maths
- NCERT Exemplar Class 11 Physics
- NCERT Exemplar Class 11 Chemistry
- NCERT Exemplar Class 11 Biology
Subject Wise NCERT Solutions
- NCERT Solutions for Class 11 Mathematics
- NCERT Solutions for Class 11 Chemistry
- NCERT Solutions for Class 11 Physics
NCERT Books and Syllabus
Also Read
Articles
Get answers from students and experts
Popular Questions
A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
An athlete in the olympic games covers a distance of 100 m in 10 s. His kinetic energy can be estimated to be in the range
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
A particle is projected at 600 to the horizontal with a kinetic energy . The kinetic energy at the highest point
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
In the reaction,
| Option 1)
|
Option 2)
|
| Option 3)
|
Option 4)
|
How many moles of magnesium phosphate, will contain 0.25 mole of oxygen atoms?
| Option 1)
0.02 |
Option 2)
3.125 × 10-2 |
| Option 3)
1.25 × 10-2 |
Option 4)
2.5 × 10-2 |
Colleges After 12th
Popular Course After 12th
Applications for Admissions are open.
JEE Main Important Chemistry formulas
ApplyAs per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
TOEFL ® Registrations 2024
ApplyAccepted by more than 11,000 universities in over 150 countries worldwide
Pearson | PTE
ApplyRegister now for PTE & Unlock 20% OFF : Use promo code: 'C360SPL20'. Valid till 31st DEC'24! Trusted by 3,500+ universities globally
JEE Main high scoring chapters and topics
ApplyAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
ApplyAs per latest 2024 syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters
News and Notifications
Back to top